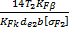для каких целей используют конические зубчатые передачи

Коническая передача и конические шестерни

Вращательное движение лежит в основе действия множества машин и механизмов, с которыми мы ежедневно сталкиваемся в жизни — от автомобилей и вертолетов до часов и детских игрушек. Довольно часто для того, чтобы нужный элемент конструкции начал вращаться, это движение необходимо не просто передать, а передать, изменив первоначальное направление оси вращения под определенным углом. Эту задачу позволяют решать конические зубчатые передачи. Они, как правило, применяются в комбинированных сложных механизмах, где используется вращательное движение с переменными углами и нагрузками. Например, в ведущих мостах автомобильной техники, в сельскохозяйственных машинах, в конструкции конвейеров и приводах промышленных станков.

Устройство конической передачи

Коническая зубчатая передача представляет собой пару конических шестерен — зубчатых колес, прошедших обработку под заданным углом. После обработки обе шестерни получают изменяемый от основания к вершине диаметр, форму, напоминающую конус, благодаря чему и получили свое название. Зубья шестерен вырезаются на боковой поверхности, при работе конические шестерни сопрягаются боковыми плоскостями. Конические пары в силу особенностей своей конструкции считаются наиболее сложными в изготовлении и сборке. К тому же они имеют не самую высокую несущую способность (например, у конической передачи при прочих равных параметрах она на 15% ниже). Тем не менее в узлах и механизмах, где необходима передача крутящего момента с угловым смещением, альтернативы им нет.

Элемент пары, передающий крутящий момент, называют ведущим (шестерней), а тот, что принимает крутящий момент — зубчатым колесом (ведомым). Результирующий угол изменения направления вращения равен сумме углов обеих конических шестерен. Наиболее часто в машинах и механизмах встречается ортогоническая коническая пара, изменяющая направление вращающего момента под углом 90 градусов (2 х45). Возможности конической передачи не исчерпываются способностью изменять направление оси вращения в широком диапазоне углов. С помощью такой конструкции можно также изменить частоту вращения (число оборотов в минуту) и мощность.

Классификация и параметры конических передач

Параметры, по которым классифицируются конические передачи, делятся на геометрические и механические. К геометрическим относятся линейные размеры и значения углов отдельных элементов деталей, образующих зубчатую пару.

К механическим параметрам конической зубчатой пары относятся следующие:

* По показателю круговой скорости вращения конические зубчатые передачи подразделяются на три основные группы: тихоходные (вращаются с низкой скоростью, не превышающей 3м/с), среднескоростные (скорость вращения до 15м/с) и высокоскоростные (скорость вращения выше 15м/с).

Если число оборотов в единицу времени у ведущего зубчатого колеса больше, чем у ведомого, передача считается понижающей; если большое число оборотов делает шестерня коническая ведомая, пара признается повышающей. Определить класс зубчатой передачи позволяет также передаточное отношение. У понижающих передач (редукторов) оно меньше единицы, у повышающих (мультипликаторов) — больше единицы.

Классификация по форме линий зубьев: коническая передача может состоять из пары конических шестерен, которые по форме линий зубьев могут быть следующими:

Для решения сложных технических задач применяются также прямозубые конические зубчатые колеса с нарезкой в форме спирали и радиальной нарезкой, шестерни с криволинейными эвольвентными зубьями (поверхность ведущего зуба перекатывается по образующей плоскости ведомого колеса), а также с зубьями циклоидной формы.

Преимущества и недостатки конических зубчатых передач

Конические зубчатые пары позволяют эффективно решать проблему изменения угла передачи крутящего момента. Среди преимуществ данного конструкционного решения выделяют:

Среди недостатков, свойственных коническим передачам, выделяют сложность изготовления зубчатых колес с нужными параметрами, в частности, из-за повышенных требований к точности нарезания зубьев. Отмечают также повышенные осевые нагрузки и нагрузки на изгиб на валы, на которых закреплены зубчатые колеса. Особенно сильно это проявляется в механизмах, где валы расположены консольно. К недостаткам относят также большую, по сравнению с другими типами зубчатых передач, массу, большие затраты на изготовление. При проектировании и производстве систем с изменяемым передаточным числом могут возникнуть трудно разрешимые проблемы, процесс передачи вращения требует регулировки, общая жесткость конструкции повышенная. И, наконец, в числе недостатков отмечают, что несущая способность у пары конических шестерен ниже на 15%, чем у цилиндрической зубчатой передачи, а нагрузочная на 20%.

Изготовление конических зубчатых колес

Главными элементами конической передачи являются зубчатые колеса — ведущее и ведомое. Они изготавливаются, преимущественно, из стали на специализированных станках с использованием нескольких технологических процессов.

Материалы и технологии

Ведущая шестерня должна иметь более высокую прочность, поэтому при изготовлении конических пар для зубчатых колес могут использоваться различные марки стали и разные методы химико-термической и термической обработки. Если для изготовления шестерни используется легированная сталь, она может быть подвергнута поверхностному уплотнению методами цианирования, цементации или азотирования. Зубчатые колеса из углеродистой стали подвергаются поверхностной закалке.

Расчеты и степени точности

В конической паре шестерен зубчатое колесо изначально характеризуется модулем (длина делительной окружности, приходящаяся на один зуб) и числом зубьев. Диаметры впадин и выступов определяют по таблице. Расчету подлежат параметры зуба (толщина, высота и длина) и его элементов — ножки и головки, а также делительный диаметр. Используется коэффициент ширины зубчатого венца, определяется угол наклона косых зубьев. В расчет также принимаются угол профиля, коэффициенты перекрытия и смещения, линии зацепления.

Для конических зубчатых колес приняты четыре степени точности из 12-ти существующих, каждая из которых определяется скоростью передаваемого вращения. Значения разрешенных круговых скоростей следующие:

Методы изготовления

Операции фрезерования и прорезки зубьев не позволяют достичь требуемой точности, поэтому их обычно дополняют обкаткой. Обкатка представляет собой способ обработки зубчатого колеса, при котором припуск на его боковых поверхностях срезается режущими кромками инструмента непосредственно в процессе главного движения резания заготовки. После обкатки пара помещается на специальный стенд, где производится притирка конических зубчатых колес. И, наконец, финальным этапом является процесс закалки зубьев.

В настоящее время оснащение современных металлообрабатывающих предприятий позволяет изготавливать конические пары любых размеров, видов и технологических профилей. Качество готовой продукции проверяется как визуально, так и в лабораторных условиях с применением передовых методов диагностики и сканирования.

Более 8 лет на рынке инжиниринговых услуг во всех сферах машиностроения.

Источник

Конические зубчатые передачи. Классификация, термины и определения

Классификация зубчатых передач

Классификация зубчатых передач

Классификация пространственных зубчатых передач

Классификация пространственных зубчатых передач

Классификация Конических зубчатых передач

Классификация Конических зубчатых передач

Классификация Конических зубчатых передач

Коническая зубчатая передача относится к классу Пространственных зубчатых передач, которые применяются для передачи вращения между валами, оси которых пересекаются или скрещиваются. К ним относятся, также: смешанные конические передачи, гиперболические передачи, винтовые передачи, гипоидные передачи, червячные передачи, спироидные передачи.

Коническая зубчатая передача осуществляет передачи между валами с пересекающимися осями, у зубчатых колёс которых аксоидные начальные и делительные поверхности конические. В конической передаче начальные поверхности совпадают с аксоидами. Линии зубьев конической передачи могут быть прямыми, тангенциальными, круговыми наклонными, круговыми «зерол», паллоидными. Вершины конусов пары конических зубчатых колес должны совпадать с точкой пересечения их осей.

Коническая передача (рис. 2.1) состоит из шестерни 1, имеющей меньшее число зубьев z1 и колеса 2 с большим числом зубьев z2, относительное движение которых можно представить как качение без скольжения друг по другу их начальных конусов (аксоидов). Линии пересечения начальных конусов и боковых поверхностей зубьев называют линиями зубьев.

Прямозубая коническая передача

Прямозубая коническая передача. Дифференциал

Оси конических колес прямозубой зубчатой передачи составляют прямой угол, и их зубья обычно нарезаются по радиусам. Прямозубые конические колёса применяют при невысоких окружных скоростях (до 2. 3 м/с, допустимо до 8 м/с). Прямозубые конические передачи обеспечивают передаточное отношение до 3.

Тангенциальная коническая передача

Если зубья конических колес прямые, но идут не по радиусам, то они называются тангенциальными и могут работать с окружной скоростью до 12 м/с.

Конические передачи с криволинейными зубьями

Конические колеса с криволинейными зубьями бывают трех разновидностей:

Коническое зубчатое колесо с круговыми зубьями, у которого угол наклона зубьев (угол спирали) в одной из точек делительной средней линии зуба равен нулю называют, также, коническое зубчатое колесо с нулевым углом наклона зубьев или «Зерол».

Различают конические зубчатые колеса с внешним нулевым, средним нулевым и внутренним нулевым углом наклона круговых зубьев, у которых соответственно равны нулю внешний делительный, средний делительный и внутренний делительный углы наклона средней линии зуба конического зубчатого колеса с круговыми зубьями.

Благодаря наклону и бочкообразной форме зубьев конические колеса с круговым зубом, более прочны, бесшумны и допускают большие отклонения при монтаже, чем прямозубые.

Конические передачи с круговыми зубьями имеют в зацеплении одновременно не менее двух зубьев, обеспечивая за счет формы зуба непрерывный контакт, бесшумность и плавность даже при высоких скоростях вращения. При этом передаваемые мощности на 30 % больше, чем у прямозубых конических колес.

Колеса типа Зерол, как и прямозубые конические колеса, работают с минимальными осевыми нагрузками. Они легко шлифуются после термообработки, благодаря чему достигается высокая точность. Поэтому колеса типа Зерол применяют в высокоскоростных передачах (с окружной скоростью более 76 м/с), используемых в авиастроении. Их можно устанавливать также в приводах, где ранее применялись прямозубые колеса.

Гипоидные зубчатые передачи

Гипоидные зубчатые передачи

Гипоидные зубчатые передачи

Гипоидные колеса за счет увеличения угла наклона зубьев β n и коэффициента перекрытия работают более плавно и бесшумно, чем передачи с круговыми зубьями. Они широко применяются в автомобилестроении, так как благодаря смещению осей шестерни и колеса дают возможность конструировать низко опущенные кузова автомобилей.

Гипоидная зубчатая передача: 1 — ведомая шестерня, 2 — ведущая шестерня Гипоидная передача (гиперболоидная) — вид винтовой зубчатой передачи, осуществляемой коническими колёсами (с косыми или криволинейными зубьями) со скрещивающимися осями (обычно 90°). Гипоидная передача имеет смещение по оси между большим и малым зубчатыми колесами. Данный тип передачи характеризуется повышенной нагрузочной способностью, плавностью хода и бесшумностью работы. Часто используется как главная передача в приводах ведущих колёс автомобилей, сельскохозяйственной техники, а также в качестве привода в станках и прочих индустриальных машинах для обеспечения высокой точности при большом передаточном числе.

Отличается от спиральной тем, что ось ведущей шестерни смещена относительно оси ведомого колеса на величину гипоидного смещения.

Спироидные зубчатые передачи

Спироидные зубчатые передачи

Типы станков для обработки конических колес

Колёса с прямыми зубьями обрабатывают, обычно, на зубодолбежных или зубострогальных станкахпо методу обкатки одним или чаще двумя резцами. На этих станках воспроизводится зацепление нарезаемого зубчатого колеса с воображаемым плоским производящим зубчатым колесом; при этом два зуба последнего представляют собой зубострогальные резцы, совершающие возвратно-поступательное движение, боковые поверхности каждого из зубьев нарезаемого зубчатого колеса формируются в результате движения резцов и обработки находящихся в зацеплении плоского и нарезаемого зубчатых колёс. Процесс нарезания зубьев происходит при движении резцов к вершине конуса заготовки, а обратный ход является холостым (в этот период резцы отводятся от заготовки).

Пример зубострогальных станков:

Конические зубчатые колёса с круговыми зубьями нарезаются на зуборезных станках методом обкатки с применением зуборезной резцовой головки, представляющей собой диск с вставленными по его периферии резцами, обрабатывающими профиль зуба с двух сторон (первая половина резцов обрабатывает одну сторону, вторая половина — другую).

Пример зуборезных станков:

Точность зубчатых колес и методы зубонарезания

Для зубчатых цилиндрических колес по ГОСТ 1643-81 Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические. Допуски установлено 12 степеней точности: с 1-й по 12-ю. Чем меньше степень, тем точнее колесо. Степени точности 1-я, 2-я и 12-я пока не регламентированы.

Для каждой степени точности установлены нормы кинематической точности, плавности зацепления и контакта зубьев.

Нормы кинематической точности определяют величину наибольшей погрешности угла поворота зубчатых колес в зацеплении за один оборот. Эта погрешность возникает при нарезании зубчатых колес за счет погрешностей взаимного расположения заготовки и режущего инструмента, а также кинематической погрешности станка. Показателями погрешности кинематической точности являются: накопленная погрешность окружного шага и колебание длины общей нормали.

Нормы плавности зацепления колеса определяют величину составляющей полной погрешности угла поворота колеса, многократно повторяющуюся за один поворот колеса. Показателями плавности являются: циклическая погрешность (средняя величина размаха колебаний кинематической погрешности за цикл), предельные отклонения основного шага и погрешность профиля.

Нормы контакта зубьев определяют точность выполнения сопряженных зубьев в передаче в зависимости от относительных размеров пятна контакта в процентах по длине и высоте зуба.

Точность каждой степени характеризуется числовыми нормами по элементам сопряжения.

Устанавливается также величина наименьшего бокового зазора между зубьями и допуск на него.

Боковым зазором называется зазор между зубьями сопряженных колес в передаче, обеспечивающий свободный поворот одного колеса относительно другого. Для передач установлено четыре вида сопряжений с гарантированным зазором: С — с нулевым, Д — с пониженным, X — с нормальным и Ш — с повышенным.

Нормы бокового зазора назначают в соответствии с эксплуатационными требованиями передачи и не зависят от норм точности.

Условное обозначение норм точности зубчатых колес состоит из четырех знаков: первые три означают степень точности в порядке их перечисления, а четвертый характеризует сочетание по боковому зазору. Например: 7-8-8-X.

Источник

Конические зубчатые передачи

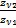
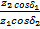
Конические зубчатые передачи применяют при пересекающихся (см. рис. 7.1, д, е, ж) или скрещивающихся осях (см. рис. 7.1, з — гипоид­ная передача). Межосевой угол Σ может изменяться в широком диапа­зоне значений (10° «> = = utgδ₂ = u 2 ;

Подставив в ранее выведенную формулу для проверочного расчета цилиндрических колес параметры эквивалентного колеса

а также введя коэффициент понижения нагрузочной способности, равный 0,85, получим формулу для проверочного расчета зубьев конических прямозубых передач на контактную усталость:

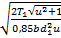
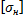
σ_н = Z K_Hβ K_Hν ≤ ,

где Z = 462·10 3 Па 1/2 для стальных колес.

Поскольку основным размером, определяющим габариты конической передачи, является внешний диаметр колеса, то формулу для проектного расчета прямозубых передач можно преобразовать и использо­вать в следующем виде:

Расчет зубьев конической передачи на усталость при изгибе. Ос­новным видом проектного расчета закрытых конических передач с низ­кой и средней твердостью зубьев является расчет на контактную уста­лость активных поверхностей зубьев, а расчет на усталость зубьев при изгибе применяется как проверочный. Исключением являются пере­дачи с высокой твердостью активных поверхностей зубьев (H > 50 HRC_э, их нагрузочная способность лимитируется изгибной прочностью); пара­метры таких передач определяют из расчета зубьев на изгиб, причем ос­новным расчетным параметром является модуль.

Проектным расчетом открытых передач также является расчет на ус­талость зубьев при изгибе.

Формула проверочного расчета на изгиб прямозубых конических передач имеет вид

где Y_F — коэффициент формы зуба, определяемый по табл. 7.7 по эквивалент­ному числу зубьев z_ν; параметр w_Ft = 2T₁ K_Fβ K_Fv / d₁b); m — средний модуль.

Формула проектного расчета на изгиб прямозубых конических пе­редач имеет вид

m = K_m ,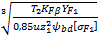

где К_т = 1,4; коэффициент неравномерности нагрузки К_Fβ определяется по графику на рис. 7.23; числом зубьев шестерни задаются, обычно z₁ = 18. 30; ψ_bd ≈ 0,166 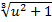(расчет ведется по шестерне).

Допускаемые напряжения для расчетов конических передач опреде­ляются так же, как для цилиндрических.

Для обеспечения примерной равнопрочности зубьев на контактную усталость и изгиб внешний окружной модуль можно ориентировочно оп­ределять по формуле

m_te ≥

(для прямозубых передач K_Fk = 0,85).

Коэффициент формы зуба для криволинейных зубьев определяется по табл. 7.7 по биэквивалентному числу зубьев

полученному двойным приведением: конического колеса к цилиндриче­скому и криволинейного зуба к прямому.

Гипоидная и спироидная передачи.Зубчатые передачи со скрещи­вающимися осями — гиперболоидные, так как их начальные кони­ческие поверхности, строго говоря, являются частью гиперболоидов вра­щения. У гипоидной передачи шестерня обычно является коническим колесом с тангенциальными или круговыми зубьями; у спироидной пере­дачи коническая шестерня-червяк имеет винтовые зубья.

Достоинства гипоидных и спироидных передач заключаются в следующем: валы и их опоры для обоих колес могут быть выведены за пределы передачи в обоих направлениях (см. рис.7.1, з), что исключает консольные нагрузки на валы; передачи характеризуются высокой нагру­зочной способностью и плавностью работы.

Характерный недостаток гиперболоидных передач — повы­шенное скольжение активных поверхностей зубьев, вызванное смещени­ем осей колес, отсюда сравнительно невысокий КПД и склонность к заеданию; такие передачи смазывают специальным противозадирным так называемым гипоидным маслом, содержащим специальные присадки. Применяют в автомобилях, тракторах, тепловозах, металлорежущих станках и других машинах. Спироидные передачи вследствие слож­ности изготовления и низкого КПД распространения не получили.

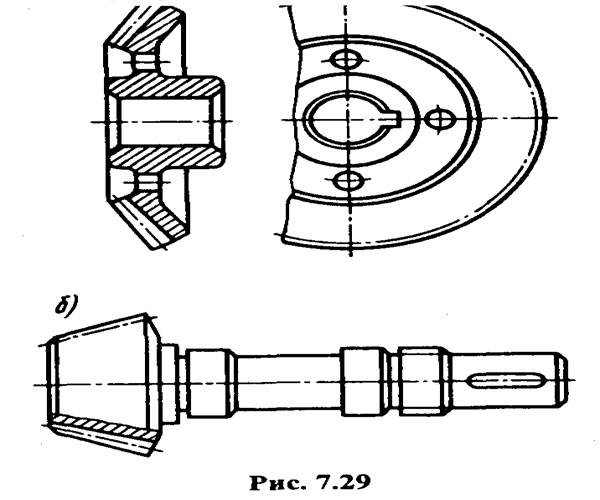
Конструкция конических колес.На рис. 7.29 показаны наибо­лее распространенная в конических редукторах конструкция колес (а) и вала-шестерни (б); насадные колеса небольшого диаметра делают моно­литной конструкции (см. рис. 7.26). Для экономии высококачественной стали применяют бандажированные конструкции колес, у которых зуб­чатый венец насаживается на колес­ный центр, изготовляемый из чугуна или стального литья.

В единичном и мелкосерийном производстве колеса небольшого (до 150 мм) диаметра изготовляют из прутков, а большого диаметра из поковок; в круп­носерийном и массовом производстве заготовками стальных колес обычно яв­ляются штамповки. Чугунные колеса всегда изготовляют отливкой. Стальные колеса большого диаметра (более 500 мм) отливают или делают сварными.

Методы образования зубьев конических колес.Нарезание прямых и тангенциальных зубьев конических колес производится методом обкатки на зубострогальных станках (рис. 7.30, а). Для понимания плоском производящем колесе, под которым понимается воображаемое коническое колесо с прямолинейным профилем зубьев и уг­лом при вершине делительного конуса 2δ = 180°; сечение зубьев вообра­жаемого колеса соответствует стандартному исходному контуру. На зу­бострогальных станках функции плоского производящего колеса выпол­няют два резца с прямолинейными кромками, движущимися возвратно-поступательно (движение резания), а резцовая головка получает согласо­ванное возвратно-вращательное движение (движение обкатки). Недос­таток зубострогальных станков — большое число холостых ходов и, следовательно, низкая производительность.

Круговые зубья нарезаются методом обкатки на специальных высо­копроизводительных станках резцовой головкой. На рис. 7.30, б показано нарезание зубьев конической шестерни 1 резцовой головкой 3; тонкими линиями показано воображаемое плоское производящее колесо 2.

Источник

Для каких целей используют конические зубчатые передачи

Одним из основных параметров зацепления Новикова является расстояние от полюса зацепления Р до точки контакта К, которое определяет положение линии зацепления ( прямой К-К параллельной осям вращения и проходящей через точку контакта К ) относительно оси мгновенного относительного вращения Р-Р. Согласно рекомендациям работы [ 14.1 ], это расстояние выбирается в зависимости от величины передаваемой мощности в пределах

Радиус окружности вершин колеса с выпуклыми зубьями:

где

где — глубина захода зубьев.

Радиус окружности впадин колеса с выпуклыми зубьями:

Радиус окружности впадин колеса с вогнутыми зубьями :

Преимущества зубчатых передач с зацеплением Новикова:

К недостаткам передач Новикова можно отнести

Конические зубчатые передачи.

Конической называется зубчатая передача, предназначенная для передачи и преобразования вращательного движения между звеньями, оси вращения которых пересекаются.

Передаточное отношение конической передачи

Так как тo

Тогда углы начальных ( делительных при х=0 ) конусов

Геометрия зацепления в конической зубчатой передаче:

Так как то :

После определения чисел зубьев эквивалентного цилиндрического зацепления, приближенный расчет геометрических параметров для внешнего торца конического зацепления можно проводить по рассмотренным выше формулам цилиндрического эвольвентного зацепления. Радиус внешней сферы (длина образующей начального или делительного конуса)

По форме линии зуба конические зубчатые передачи различаются на: прямозубые; косозубые; с круговым зубом; с эвольвентной линией зуба; с циклоидальной линией зуба

Преимущества и недостатки конических зубчатых передач.

Червячные зубчатые передачи.

Виды червячных передач и червяков ( по ГОСТ 18498-73 ).

Геометрия зацепления цилиндрической червячной передачи

Связь между ходом винтовой линии pz1 и шагом многозаходного винта p1

Расчет геометрии зацепления.

Расчет геометрических параметров.

витков червяка

зубьев червячного колеса в средней торцовой плоскости

червяка

червячного колеса

Геометрические показатели качества зацепления.

Преимущества и недостатки червячных зубчатых передач

Зубчатые передачи с циклоидальными профилями.

Теорема Камуса доказывает что профили выполненные по циклоидальным кривым будут при определенных условиях сопряженными и взаимоогибаемыми. Теорема Камуса. Кривые, описываемые какой-либо точкой жестко связанной с некоторой вспомогательной центроидой при перекатывании ее по центроидам, определяющим относительное движение рассматриваемых звеньев, будут взаимоогибаемыми в относительном движении этих звеньев.

Преимущества и недостатки циклоидального зацепления

1. Какие зубчатые передачи используются для передачи вращения между параллельными и пересекающимися осями?(стр.1)

2. Чем отличаются эвольвентные зубчатые передачи от передач с круговинтовым зацеплением Новикова?(стр.1)

3. Укажите достоинства и недостатки зубчатых передач Новикова (стр.2-3)

4. Для каких целей используются конические зубчатые передачи?(стр.3-4)

5. Каковы особенности геометрии конических колес и передач?(стр.4-5)

6. Укажите достоинства и недостатки конических зубчатых передач(стр.6)

7. Как определить углы вершин начальных конусов в конической передаче при известном передаточном отношении и межосевом угле? (стр.4)

8. Какие виды червячных передач используются в механизмах?(стр.6-7)

9. Какими особенностями кинематики червячных передач вызвано скольжение зубьев?(стр.8-10)

Источник