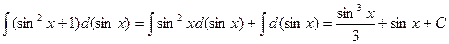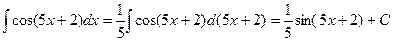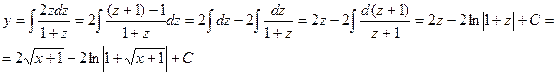для каких функций существует первообразная на заданном интервале

Первообразная функция и неопределенный интеграл

Первообразная

Определение первообразной функции

Можно прочесть двумя способами:

Правила вычисления первообразных

Запомни!

Любая функция F(x) = х 2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.

Связь между графиками функции и ее первообразной:

Неопределенный интеграл

Определение:

Свойства неопределённого интеграла

Таблица первообразных и неопределенных интегралов

Функция

Первообразная

F(x) + C

Неопределенные интегралы

\int f(x) dx = F(x) + C

Формула Ньютона–Лейбница

Пусть f (х) данная функция, F её произвольная первообразная.

То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.

Площадь криволинейной трапеции

Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

Площадь криволинейной трапеции находят по формуле Ньютона-Лейбница:

Источник

Для каких функций существует первообразная на заданном интервале

Изучая математику, мы не раз сталкивались со взаимно-обратными операциями.
Примерами взаимно-обратных операций являются:

Операция, обратная дифференцированию, называется интегрированием, а процессом, обратным нахождению производной, является процесс нахождения первообразной.

Или Первообразной для функции F(x) называется функция, производная которой равна данной.

Зад ача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. Важную роль в решении этой задачи играет признак постоянства функции:
Если

Все первообразные функции а можно записать с помощью одной формулы, которую называют общим видом первообразных для функции f.

Основное свойство первообразных:
Любая первообразная для функции f на промежутке I может быть записана в виде

где F(x) – одна из первообразных для функции f(х) на промежутке I, а С – произвольная постоянная.

В этом утверждении сформулированы два свойства первообразной
1) какое бы число ни подставить вместо С, получим первообразную для f на промежутке I;
2) какую бы первообразную Ф для f на промежутке I ни взять, можно подобрать такое число С, что для всех х из промежутка I будет выполнено равенство Ф(х) = F(x) + C.

Геометрический смысл первообразной

Пример 1. Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1).

Решение: F'(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F'(x) = f(x), следовательно, F(x) является первообразной для функции f(x).

Пример 2. Найти все первообразные функции f(x): f(x) = х 4 + 3х 2 + 5

Решение: Используя таблицу и правила нахождения первообразных, получим:

Ответ:

Задание № 1
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю

Источник

Первообразная и неопределенный интеграл, их свойства

Определение первообразной

Определение неопределенного интеграла

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

∫ f ( x ) d x ‘ = F ( x ) + C ‘ = f ( x )

∫ d ( F ( x ) ) = ∫ F ‘ ( x ) d x = ∫ f ( x ) d x = F ( x ) + C

∫ f ( x ) ± g ( x ) ) d x = ∫ f ( x ) d x ± ∫ g ( x ) d x

Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.

Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:

k · ∫ f ( x ) d x ‘ = k · ∫ d ( x ) d x ‘ = k · f ( x ) ∫ f ( x ) d x ± ∫ g ( x ) d x ‘ = ∫ f ( x ) d x ‘ ± ∫ g ( x ) d x ‘ = f ( x ) ± g ( x )

Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.

Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.

Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.

Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.

Решение

Используя таблицу производных основных элементарных функций получаем

d ( ln x ) = ( ln x ) ‘ d x = d x x = f ( x ) d x ∫ f ( x ) d x = ∫ d x x = ∫ d ( ln ( x ) )

Ответ: f ( x ) = 1 x = ln ( x ) + 1

Необходимо найти неопределенный интеграл ∫ 2 sin x 2 cos x 2 d x и проверить результат вычисления дифференцированием.

Решение

Используем таблицу производных для тригонометрических функций, получим:

Проверим полученный результат дифференцированием.

В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Подробнее эту тему мы рассмотрим в следующем разделе «Таблица первообразных (таблица неопределенных интегралов)».

Источник

Первообразная

Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого .

Операция нахождения первообразной функции f(x), называется интегрированием.

Неопределенный интеграл

Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:

,

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.

Дифференциал-произвольное, бесконечно малое приращение переменной величины.

Свойства неопределённого интеграла

Таблица основных неопределённых интегралов

В виде

,

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.

Определённый интеграл

Определенный интеграл— Приращение одной из первообразных функции f(x) на отрезке [a;b].

Общий вид определённого интеграла:

где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал

Свойства определённого интеграла: см. св-ва определённого интеграла.

Определённый интеграл вычисляется по формуле Ньютона –Лейбница:

Применение определённого интеграла:

1. Нахождение площади криволинейной трапеции

2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е

Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.

Решение:

3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.

Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.

Решение:

Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.

Источник

Раздел 5. Неопределенный интеграл.

Первообразная. Неопределенный интеграл.

Определение: Функция F(x), дифференцируемая на интервале (a, b), называется первообразной для функции f(x) на данном интервале, если для всех значений х, принадлежащих этому интервалу, выполняется равенство: .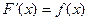

Например: является первообразной для , так как , но , тоже первообразная функции и т.п., следовательно, вся совокупность функций есть первообразные функции .

Если для некоторой функции существует хотя бы одна первообразная, то можно утверждать, что для нее существует бесчисленное множество первообразных, различающихся между собой на постоянные величины.

Определение: Совокупность всех первообразных функций F(x)+C для функции f(x) называется неопределенным интегралом этой функции и обозначается

При этом f(x) называют подынтегральной функцией. А выражение f(x)dx – подынтегральным выражением.

Процесс нахождения первообразной функции называется интегрированием, причем аргумент х подынтегральной функции выступает здесь также в качестве переменной интегрирования.

Интегрирование – действие, обратное дифференцированию, его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной.

Всегда ли существует первообразная для заданной функции f(x)?

Примем без доказательства, что если функция непрерывна на (a, b), то она имеет первообразную, а, следовательно, и неопределенный интеграл на этом интервале.

Геометрический смысл неопределенного интеграла.

Пример: Известно, что график функции f(x) проходит через точку А(2,5), а скорость изменения данной функции имеет вид 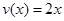. Построить график функции f(x).

Так как функция f(x) является первообразной для функции v(x), то значение ее можно найти, взяв неопределенный интеграл от функции v(x). . Ответ получен с точностью до константы С, найти которую можно из дополнительного условия: график функции f(x) должен проходить через точку А(2,5). Подставим в выражение функции f(x) координаты точки А и получим: . Тогда искомая функция будет иметь вид: — это парабола.

Чтобы научиться находить первообразную функции, в первую очередь необходимо выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она получается в результате обращения соответствующих формул дифференцирования. Например, если , то . Далее необходимо знать свойства неопределенного интеграла и освоить простейшие приемы интегрирования.

Таблица основных интегралов

Свойства неопределенного интеграла

Рассмотрим простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции.

1) Производная от неопределенного интеграла функции f(x) равна самой этой функции:

.

2) Дифференциал от неопределенного интеграла равен подынтегральному выражению:

.

3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до константы:

.

Пример:

4) Постоянный множитель можно выносить за знак интеграла:

.

Пример:

5) Интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций, т.е.

Пример: .

Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если , то , где — произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.

Пример: , поэтому

, . Сравните с .

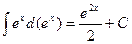
В интегральном исчислении нет универсального способа интегрирования. Применение различных методов приводит данный интеграл к табличному, который надо узнать с учетом свойства инвариантности.

Методы интегрирования

1) Непосредственное интегрирование.

Этот метод заключается в прямом использовании табличных интегралов и их свойств.

Пример:

Пример:

Пример:

Следует отметить, что хотя при взятии каждого интеграла появляется своя константа, однако окончательный результат выражается через одну произвольную постоянную, являющуюся их линейной комбинацией.

Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул.

Пример:

Пример:

Пример;

3) Метод подведения под знак дифференциала.

В данном методе для приведения искомого интеграла к табличному виду преобразовывают дифференциал аргумента функции. Дифференциал не меняется, если к переменной прибавить или отнять постоянную величину, а если переменную увеличить в несколько раз, то дифференциал необходимо умножить на обратную величину, то есть .

Пример:

Пример:

Пример:

4) Метод выделения полного квадрата из квадратичного трехчлена.

Пример:

Пример: .

5) Метод замены переменных

Замечание.Подведение под знак дифференциала является частным случаем замены переменной, так как выполняются те же действия, только не вводится новая переменная.

Пример:∫ .

Введем новую переменную z=x+2. Найдем из этого уравнения связь между дифференциалами старой и новой переменной. Для этого продифференцируем левую и правую часть уравнения z=x+2. Получим: dz=dx.

Тогда наш интеграл примет вид:

= =ln│z│+c= ln│x+2│+c

Пример : .

Если внимательно посмотреть на числитель и знаменатель подынтегрального выражения, то можно заметить, что числитель с точностью до постоянного множителя представляет собой дифференциал знаменателя. Тогда можно ввести новую переменную z=x +7. Тогда связь между dz и dx можно найти из последнего выражения, продифференцировав левую и правую его части: dz=2x∙dx. Тогда наш интеграл примет вид табличного интеграла:

= = = ln│z│+c= ln│x +7│+c

Перейдя к старой переменной в конечном результате, получим искомое решение интеграла.

Пример:

Введем замену переменной: , так, чтобы избавиться от квадратного корня в знаменателе. Тогда . Затем продифференцируем данное выражение: . Значит, .

Подставим замену в исходное выражение и возьмем интеграл:

Пример:

Введем замену переменной: .

Продифференцируем данное выражение: .

Выразим dx через dz. Получим: .

Подставим замену в исходное выражение и возьмем интеграл:

Пример: .

Введем замену u=cosx. Продифференцируем данное выражение:

Пример: .

Используем подстановку u=sinx и du=cosx∙dx. Тогда

= = =

6) Интегрирование по частям.

Этот метод основан на использовании формулы интегрирования по частям: , где u(x) и v(x) – функции, имеющие непрерывные производные в некотором промежутке. При использовании данной формулы нахождение исходного интеграла сводится к нахождению интеграла , причем эту процедуру имеет смысл проводить лишь в том случае, если новый интеграл проще исходного и может быть найден с использованием рассмотренных выше способов интегрирования.

1) Интегралы вида , , , где

Р(х)- многочлен решаются по частям при замене dv=P(x)dx, и u – другие сомножители.

Пример:

Подынтегральное выражение подставим виде udv. Через u следует обозначить lnx, а через dv=xdx.

Тогда du= 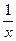dx, а v= . Согласно формуле интегрирования по частям:

Пример: .

Обозначим u=arcsinx, тогда .

Пусть dv=dx, тогда .

Искомый интеграл будет равен:

Интеграл в правой части можно взять методом подстановки.

Введем подстановку: 1-x =z, dz=-2xdx. Тогда

Теперь подставим полученную формулу в первоначальный интеграл:

= .

2) Интегралы вида , , , где

Р(х) –многочлен, к – константа решаются по частям, при обозначении u=P(X), а dv – все остальные сомножители.

Пример: , где обозначили u=x, тогда , а , тогда .

3) Интегралы вида , .

Здесь надо сначала сделать замену переменной, а затем интегрировать по частям.

Пример: , где сделали сначала замену переменной x=t², тогда dx=2tdt, а затем взяли интеграл по частям по аналогии с предыдущим примером.

4) Интегралы вида , , где a и b – константы берутся следующим образом: за u можно взять , sin(bx) или cos(bx). Замена производится дважды.

Пример :

Обозначим u=e , тогда du=e dx.

Обозначим dv=cosxdx, тогда v= =sinx.

Применим формулу интегрирования по частям:

— .

Тогда

Подставим значение полученного интеграла в выражение исходного интеграла, получим:

Перенесем последний интеграл правой части в левую сторону уравнения и получим:

, тогда = .

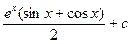
Следует отметить, что, несмотря на то, что последний способ интегрирования представляется наиболее сложным из рассмотренных, универсальным он не является, и его следует использовать лишь в тех случаях, когда предыдущие способы не дают необходимого результата.

Источник