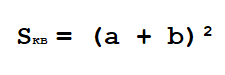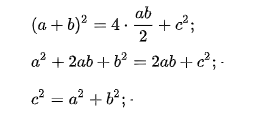для каких треугольников применяется теорема пифагора
Теорема Пифагора: история, формулы и доказательства
Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.
Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.
После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.
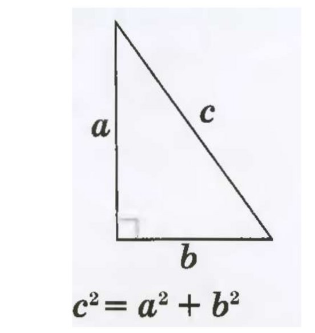
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть ВС = а; АС = b; АВ = с.
Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:
А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему «Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора».
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.
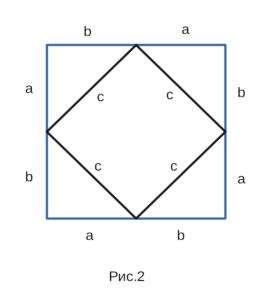
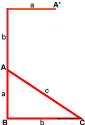
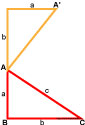
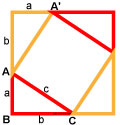
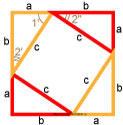
Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.
Площадь этого квадрата можно будет найти благодаря формуле:
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:
Итак, теорема Пифагора доказана.
2. Доказательство Евклида
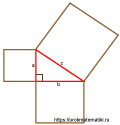
Доказательство Евклида также называется «Пифагоровы штаны». Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.
На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.
В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе «Учебники по геометрии за 8 класс».
Пример задачи на применение теоремы Пифагора
Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.
Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:
АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.
Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу «ГДЗ и решебники по геометрии за 8 класс».
А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе «Онлайн уроки за 8 класс по геометрии». Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.
Теорема Пифагора
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Пошаговое доказательство:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?
значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136
Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?
Ответ: треугольник не является прямоугольным.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Теорема Пифагора.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника.
Будет полезно сохранить таблицу Пифагора.
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
Для всякой тройки положительных чисел a, b и c, такой, что

существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей, аксиоматические и экзотические доказательства (например,
с помощью дифференциальных уравнений).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим
её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC.


или 
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

треугольника так, как показано на рисунке
Четырёхугольник со сторонами c – квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
записать следующее соотношение для бесконечно
малых приращений сторон с и a (используя подобие
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b). Тогда для константы интегрирования получим:
Теорема Пифагора
Теорема Пифагора является одной из важнейших теорем в геометрии.
Формулировка у теоремы такая:
в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Зная формулировку теоремы Пифагора и две стороны прямоугольного треугольника:
два катета либо катет и гипотенузу, можно найти третью сторону треугольника,
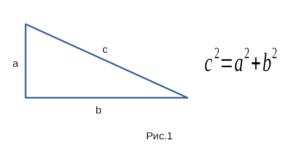
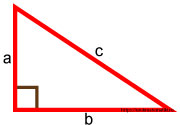
соответственно: гипотенузу либо катет. На рисунке 1 изображен
прямоугольный треугольник и формулировка теорема Пифагора.
Доказательство теоремы Пифагора
Для доказательства этой теоремы, нарисуем прямоугольный треугольник.
Ради удобства обозначим гипотенузу латинской буквой с, а катеты латинскими
буквами a и b. Докажем, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов, или иначе \( c^2=a^2+b^2 \).
Теорема доказана.
Следствия из теоремы Пифагора
У этой теоремы много следствий, которые используются при доказательстве
других теорем и некоторых свойств. Перечислим основные из них:
Теорема Пифагора
Теорема Пифагора — пожалуй, одна из самых известных теорем в математике вообще и геометрии в частности. На самом деле несмотря на то, что она названа именем Пифагора, она была известна еще за тысячу лет до него.
Если вы построите вместо квадратов любые подобные фигуры, допустим полуокружности, то сумма этих площадей, построенных на катетах, все равно будет равняться площади фигуры, построенной на гипотенузе.
Доказательство теоремы Пифагора
На сегодняшний день известно более 200 различных доказательств теоремы Пифагора. Мы воспользуемся одним из них.
Преобразовав описанное выше в формулу, получаем:
a + b 2 = 4 · 1 2 a b + c 2
Раскроем формулу квадрата суммы:
a 2 + b 2 + 2 a b = 2 a b + c 2
a 2 + b 2 + 2 a b = 2 a b + c 2
Мы доказали теорему Пифагора.
Задачи на тему «Теорема Пифагора»
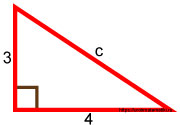
Египетский треугольник
Требуется найти его гипотенузу.
Решение:
Обозначим гипотенузу как c и воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
3 2 + 4 2 = c 2
9 + 16 = c 2
25 = c 2
c = 5
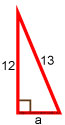
Пифагорова тройка
Требуется найти второй катет.
Обратите внимание, что в первом и втором примерах стороны треугольников получились целыми числами. Такие числа, которые удовлетворяют теореме Пифагора, называются пифагоровыми тройками.
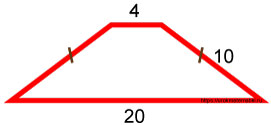
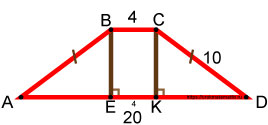
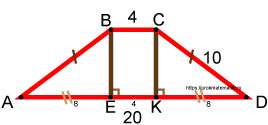
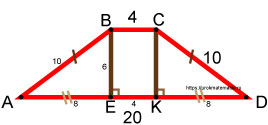
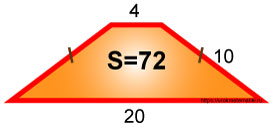
Равнобедренная трапеция
Так как наша трапеция равнобокая, то левый и правый треугольники равны между собой, т.к. имеют одинаковые катеты и одинаковые гипотенузы. По признакам равенства прямоугольных треугольников они равны. Это означает, что отрезки AE и KD равны между собой.
Применение теоремы Пифагора
Наиболее частое применение теоремы Пифагора можно увидеть в строительстве. В современные дальномеры встраивается функция, косвенно определяющая размеры стороны (треугольника) при измерении двух других сторон.
Рассмотрим два теоретических примера, когда необходимо произвести расчёт конструкции крыши, а в другом примере научимся позиционировать стены дома относительно друг друга под углом 90°.
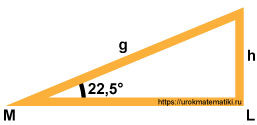
Расчет стропильной системы крыши
Задача крайне упрощённая для точных расчётов стропильной системы крыши, но достаточно понятная, чтобы донести принципы расчёта по теореме Пифагора.
Требуется найти длину стропила ( g ) и высоту стойки ( h ).
Теперь подставляем в формулу известные значения для определения высоты стойки ( h ) по теореме синусов:
sin 22,5° h = sin 67,5° ML
h = 5 · sin 22,5° sin 67,5° = 2.0710678118655
Также по теореме синусов можно найти и длину ( g ), но нас интересует теорема Пифагора.
Поэтому зная, что квадрат гипотенузы (в нашем случае это g ) равен сумме квадратов катетов (в нашем случае это h и расстояние между точками ML ), получаем:
Подставляя в формулу ранее вычисленные и известные значения, получаем:
Египетский треугольник
Ещё одним примером практического применения теоремы Пифагора в строительстве может служить использование египетского треугольника.
Соедините верёвку в треугольник, как показано на изображении, и натяните стороны полученного треугольника.
Угол между сторонами 3, 4 всегда будет равен 90°. По нему можно разметить стены или фундамент будущего дома.