для какой цели в формулах используют трехмерные ссылки в excel
Использование трехмерных ссылок
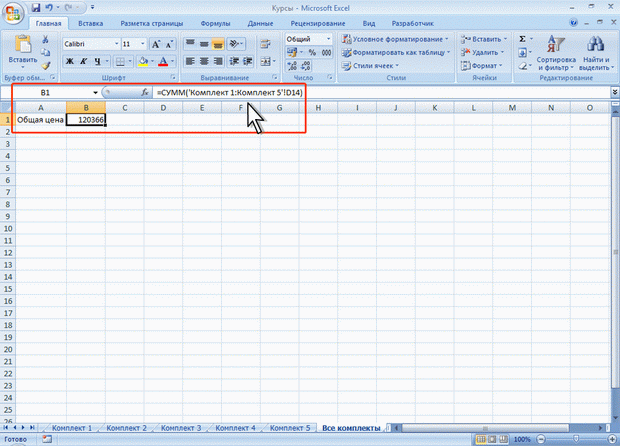
Трехмерные ссылки используются при выполнении действий с данными из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка включает в себя ссылку на ячейку или диапазон, перед которой ставятся имена листов. При этом в формулу включаются все листы, хранящиеся между начальным и конечным именами, указанными в ссылке. Например, формула =СУММ(Июль:Сентябрь!С2) суммирует все значения, содержащиеся в ячейке С2 на всех листах в диапазоне от Июль до Сентябрь включительно (рис. 6.17).
увеличить изображение
Рис. 6.17. Использование трехмерных ссылок
Трехмерные ссылки могут быть использованы для создания ссылок на ячейки на других листах, определения имен и создания формул с использованием следующих функций: СУММ, СРЗНАЧ, СЧЁТ, МАКС, МИН, ПРОИЗВЕД, и некоторых других.
Использование имен ячеек и диапазонов
Использование имен
Имя – слово или строка знаков, представляющих ячейку, диапазон ячеек, формулу или константу. Имена можно использовать в любом листе книги.
Присваивание имен
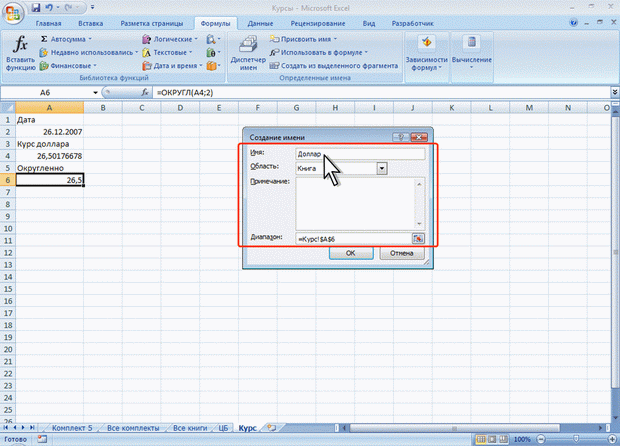
Имя можно присвоить ячейке или диапазону ячеек.
увеличить изображение
Рис. 6.18. Присвоение имени ячейке
Для удобства работы рекомендуется создавать имена короткие и хорошо запоминающиеся. Первый знак в имени должен быть буквой или знаком подчеркивания. Остальные знаки имени могут быть буквами, числами, точками и знаками подчеркивания. Пробелы не допускаются. Также не допускаются имена, которые имеют такой же вид, как и ссылки на ячейки, например Z$100 или R1C1. В имени может быть больше одного слова. В качестве разделителей слов могут быть использованы знаки подчеркивания и точки, например: Год_2007 илиГод.2007. Имя может содержать до 255 знаков. Имя может состоять из строчных и прописных букв, но Excel их не различает.
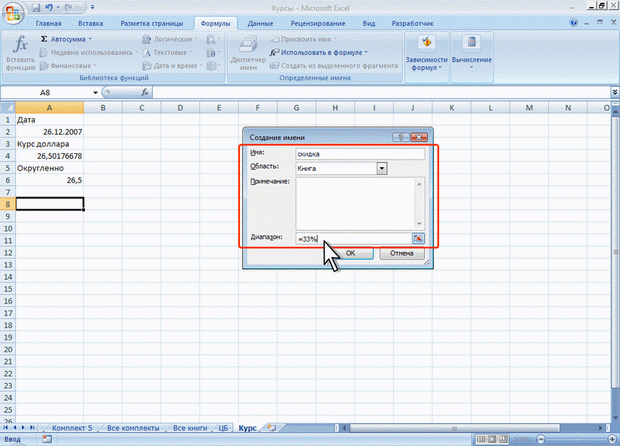
Имя можно присвоить формуле или постоянному значению (константе). Например, имя “Скидка”, которому присвоено значение 33процента, можно использовать в любом месте для вычисления цены со скидкой.
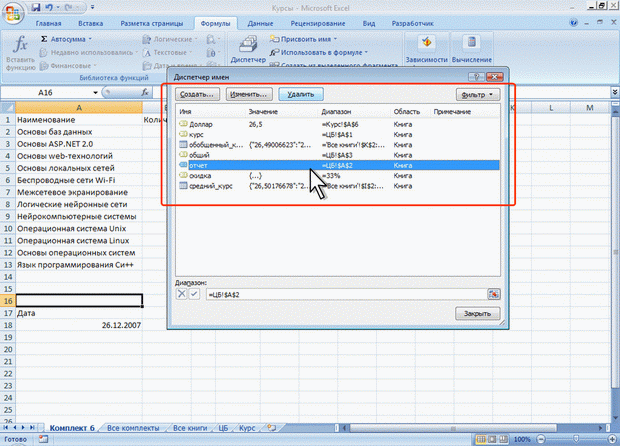
Для присвоения имени формуле или константе в поле Диапазон окна Создание имени следует ввести знак равенства (=) и формулу или константу (рис. 6.19).
увеличить изображение
Рис. 6.19. Присвоение имени константе
Применение имен
При создании формул короткие имена можно вводить с клавиатуры.
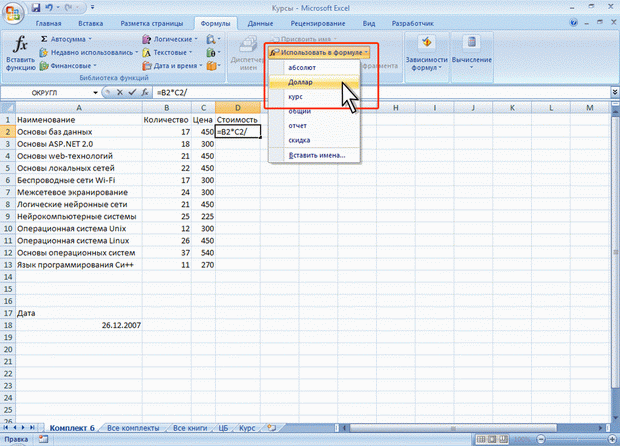
Во избежание возможных ошибок при использовании имен в процессе создания формулы следует в группе Определенные имена вкладкиФормулы щелкнуть кнопку Использовать в формуле и выбрать нужное имя в списке имен (рис. 6.20).
увеличить изображение
Рис. 6.20. Вставка имени в формулу
Если нужное имя не отображается в списке, выберите команду Вставить имена (см. рис. 6.20), а затем в окне Вставка имени выберите вставляемое имя.
Имена ячеек являются абсолютными ссылками.
Удаление имени
Ненужное или ошибочное имя можно удалить.
увеличить изображение
Рис. 6.21. Удаление имени
Трехмерные ссылки в формулах Excel
Если в формуле ссылка ссылается на другой лист или другую книгу, то такая ссылка в Excel считается трехмерной.
Чаще всего пользователь Excel использует формулы, которые обрабатывают текущие данные одного и того же листа где находиться сама формула (например, =В32 или =АВ123). Тогда исходные адреса ячеек и формулы лежат в одной плоскости, поэтому их адреса являются двумерными.
Расширение адреса ссылки за границы текущего листа (например, =Лист2!В32), позволяет выступить в трехмерном пространстве ячеек. Рассмотрим конкретные примеры.
Пример использования трехмерных ссылок в Excel
Создайте новую книгу с 4-ма листами: «1 квартал», «Январь», «Февраль», «Март». На каждом листе введите в диапазон A1:A4 одинаковые значения: «Оплата», «Телефон», «Интернет», «Спутниковое ТВ».
В ячейках B2:B4 каждого листа месяца введите разные суммы определяющие расходы на конец месяца. Сумам присвойте денежный формат ячеек.
На листе «1 квартал» в диапазон B2:B4 введите трехмерные формулы, которые суммируют суммы каждого месяца соответственно типу расходов. А в ячейке B6 просуммируйте итоговую сумму расходов двумерной формулой.
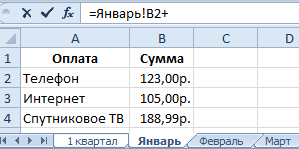
Вводим трехмерную формулу. Способ1:
Изначально можно ввести трехмерную формулу в ячейку B2 листа «1 квартал» написав все названия листов вручную: =Январь!B2+Февраль!B2+Март!B2.
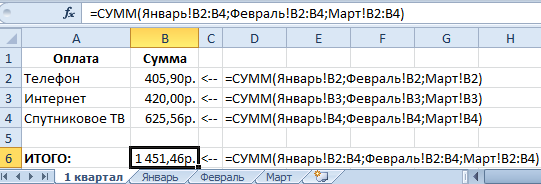
Способ 2: Так же можно использовать в формуле функцию СУММ(). Например, =СУММ(Январь!B2;Февраль!B2;Март!B2).
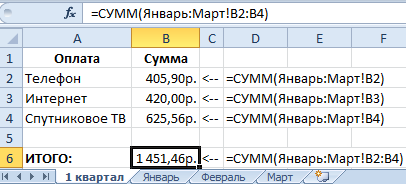
Способ 3: Можно использовать сокращенный вариант аргументов функции СУММ() с помощью указания трехмерных диапазонов. Например, =СУММ(Январь:Март!B2). Данный способ показывает, как можно эффективно использовать диапазоны в трехмерных ссылках.
Обратите внимание на формулу в ячейке B6 данного рисунка. Пример, =СУММ(Январь:Март!B2:B4).
Все три способа ввода трехмерных формул имеют свои преимущества и недостатки. Например, если у нас мало используется листов и ячеек с небольшим количеством данных в диапазонах, то удобнее использовать 1 способ. А если много листов и большие объемы данных (например, диапазон B2:B527). Тогда рационально использовать способ №3.
Функция ДВССЫЛ в трехмерных ссылках: примеры использования
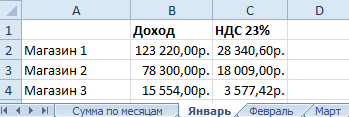
Создайте листы и заполните их данными для всех месяцев одинаково, лишь числовые значения должны отличаться, так как указано на рисунке:
На листе «Сумма по месяцам» следует составить таблицу, так чтобы отдельно отображалась сумма доходов и сумма налогов соответствующего месяца.
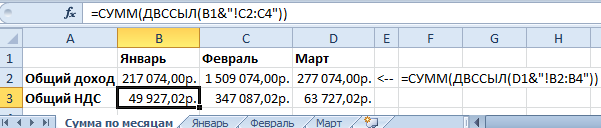
Внимание! Названия заголовков столбцов в диапазоне B2:D2 должны совпадать с названиями имен листов. Это даст нам возможность использовать в формуле очень удобную функцию =ДВССЫЛ(), которая конвертирует текст в адрес ссылки.
Символ «&» (конкатенации) соединяет два текста в один. Так же обратите внимание, что параметры функции ссылаются на ячейку B2, которая содержит навязывание месяца и соответственно имя нужного нам листа – «Январь». Текстовое значение ячейки B2 конвертируется в адрес ссылки с помощью функции =ДВССЫЛ() и в результате получаем адрес трехмерной ссылки «Январь!B2:B4».
Основы вычислений
Использование ссылок в формулах
Ссылки на ячейки других листов и книг
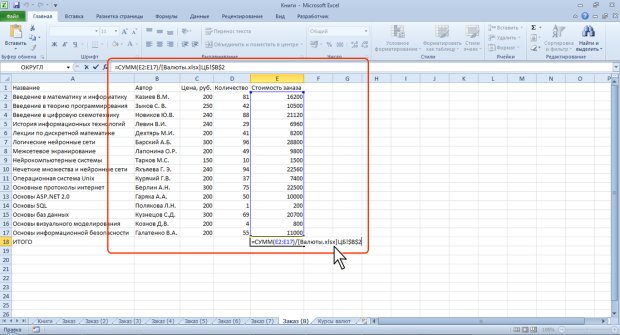
Например, в формуле в ячейке Е18 в таблице на рис. 6.13 использована ячейка В2 листа Курсы валют текущей книги.
Относительные и абсолютные ссылки
По умолчанию ссылки на ячейки в формулах относительные, то есть адрес ячейки определяется на основе расположения этой ячейки относительно ячейки с формулой. При копировании ячейки с формулой относительная ссылка автоматически изменяется. Именно возможность использования относительных ссылок и позволяет копировать формулы.
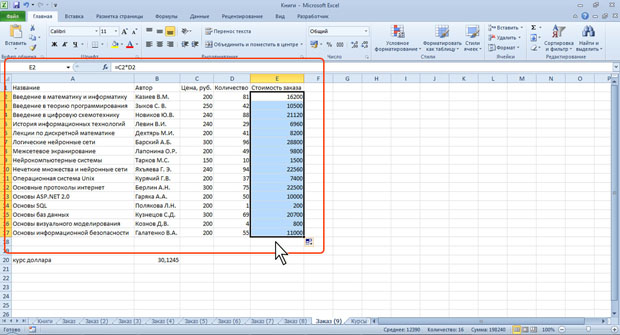
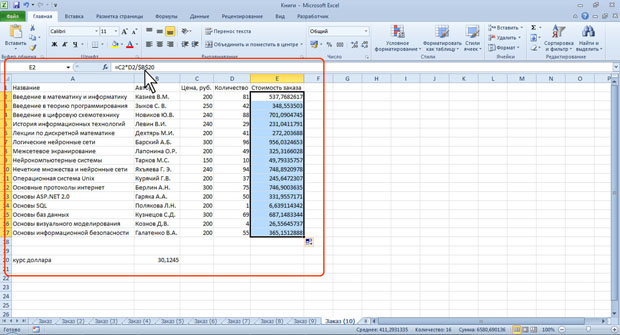
В некоторых случаях использование относительных ссылок недопустимо. Например, в таблице на рис. 6.16 при копировании ячейки Е2 на нижерасположенные ячейки ссылка на ячейки С2 и D2 должны изменяться, а ссылка на ячейку В20 должна оставаться неизменной.
Чтобы ссылка на ячейку была абсолютной, после указания ссылки на ячейку следует нажать клавишу F4. Ссылку можно преобразовать из относительной в абсолютную и при редактировании ячейки с формулой. К заголовкам столбца и строки в адресе ячейки следует добавить служебный символ $. Например, для того чтобы ссылка на ячейку В20 стала абсолютной, необходимо ввести $В$20.
Ссылка может быть не только относительной или абсолютной, но и смешанной.
Ссылка формата A$1 является относительной по столбцу и абсолютной по строке, т.е. при копировании ячейки с формулой выше или ниже, ссылка изменяться не будет. А при копировании влево или вправо будет изменяться заголовок столбца.
Ссылка формата $A1 является относительной по строке и абсолютной по столбцу, т.е. при копировании ячейки с формулой влево или вправо ссылка изменяться не будет. А при копировании выше или ниже будет изменяться заголовок строки.
Например, в ячейке Е2 таблицы на рис. 6.16 достаточно было ввести смешанную ссылку В$20.
Использование трехмерных ссылок
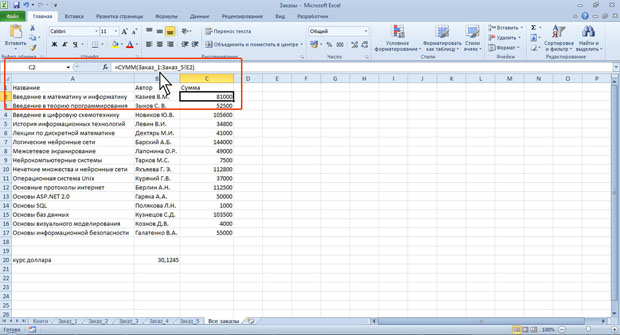
Трехмерные ссылки используются при выполнении действий с данными из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка включает в себя ссылку на ячейку или диапазон, перед которой ставятся имена листов. При этом в формулу включаются все листы, хранящиеся между начальным и конечным именами, указанными в ссылке. Например, в ячейке C2 формула =СУММ(Заказ_1:Заказ_5!Е2) суммирует все значения, содержащиеся в ячейке E2 на всех листах в диапазоне от Заказ_1 до Заказ_5 включительно (рис. 6.17).
Трехмерные ссылки могут быть использованы для создания ссылок на ячейки на других листах, определения имен и создания формул с использованием следующих функций: СУММ, СРЗНАЧ, СЧЁТ, МАКС, МИН, ПРОИЗВЕД, и некоторых других.
Хитрости использования ссылок на ячейки в Excel
Стили ссылок
Ссылки в Excel бывают двух стилей:
Ссылка стиля А1 использует буквенную нумерацию столбцов и числовую нумерацию строк. Ниже приведены примеры ссылок стиля А1 из справочной системы Excel:
Ячейка или диапазон
Ячейку в столбце A и строке 10
Диапазон ячеек: столбец А, строки 10-20.
Диапазон ячеек: строка 15, столбцы B-E.
Все ячейки в строке 5.
Все ячейки в строках с 5 по 10.
Все ячейки в столбце H.
Все ячейки в столбцах с H по J.
Диапазон ячеек: столбцы А-E, строки 10-20.
Смысл использования этого непривычного способа записи ссылок станет понятен, когда мы разберемся с относительными и абсолютными ссылками.
Абсолютные и относительные ссылки
В зависимости от поведения при копировании ячеек различают абсолютные, относительные и смешанные ссылки.
Относительные ссылки при копировании ячейки будут автоматически корректироваться, “сдвигаться” относительно ячейки так, что смещение влияющей ячейки (той, на которую мы ссылаемся) относительно зависимой (той, в которую введена формула сос ссылкой) останется прежним.
Например, в ячейку А1 введена формула =В1*2.
При копировании формулы в ячейку А2 она будет автоматически откорректирована на формулу =В2*2.
Как в первом, так и во втором случае, ссылка смещена относительно ячейки с формулой на одну ячейку вправо и находится в той же строке.
Если мы скопируем формулу в ячейку С1, формула превратится в =D1*2. Теперь корректировка коснулась столбца, а смещение осталось прежним.
Абсолютные ссылки при копировании не корректируются.
Формула из нашего примера в абсолютной нотации будет выглядеть так: =$B$1*2.
Теперь, куда бы мы ни копировали формулу, она все равно будет ссылаться на ячейку В1.
Повторное нажатие F4 преобразует ссылку в смешанную. Преобразования происходят в такой последовательности:
Вы уже наверняка догадались, что у смешанных ссылок “закреплены” либо столбец, либо строка, в зависимости от того, перед чем стоит знак доллара.
Стиль R1C1 записи гораздо удобнее, например, если вы работаете с макросами и используете циклы обхода ячеек.
Зачем нужны абсолютные и смешанные ссылки?
Допустим, нам нужно проанализировать структуру продаж за два года.
Данные по продажам представлены в таблице следующего вида
Трехмерный движок на формулах Excel для чайников
В этой статье я расскажу, как мне удалось портировать алгоритм рендера трехмерных сцен на формулы Excel (без макросов).
Для тех, кто не знаком с компьютерной графикой, я постарался как можно проще и подробнее описать все шаги. В принципе, для понимания формул должно быть достаточно знания школьного курса математики (+умение умножать трехмерную матрицу на вектор).
Также я сделал небольшое веб-приложение, где можно потренироваться в создании формул для произвольных фигур и сгенерировать свой файл Excel.
Осторожно: 19 картинок и 3 анимации под катом.
Что получилось
В случае скачивания своего Excel-файла с ObservableHQ, ячейки необходимо раскрасить вручную. Нужно выделить все маленькие квадратные ячейки и выбрать «Условное форматирование» → «Цветовые шкалы».
Ray marching
Алгоритм Ray Marching был популяризован Iñigo Quilez в 2008 году после презентации «Rendering Worlds with Two Triangles» о компактном трехмерном движке для демосцены.
После этого Iñigo Quilez создал сайт Shadertoy, и большая часть отправляемых туда работ использует описанную методику. Оказалось, что при помощи нее можно создавать фотореалистичные сцены, посмотрите, например эту галерею.
Ray Marching — это очень простой в реализации и эффективный алгоритм, позволяющий рендерить довольно сложные сцены. Почему тогда он не используется на видеокартах? Дело в том, что видеокарты заточены под работу с трехмерными фигурами, состоящими из треугольников, для чего Ray Marching не так эффективен.
Update: См. также этот комментарий от DrZlodberg о недостатках этого метода.
Принцип работы движка
Описание объекта
Можно придумать три способа описания трехмерного объекта:
SDF получает на вход точку пространства и возвращает расстояние до ближайшей точки объекта. Для точек внутри она равна расстоянию до границы объекта со знаком «минус»
Нахождение пересечения луча и объекта
Допустим, у нас есть луч, исходящий из камеры, и мы хотим найти точку его пересечения с объектом.
В голову приходит несколько способов найти эту точку:
Это простой алгоритм, который работает только с SDF.
Давайте параметризуем луч по расстоянию от его начала функцией .
Тогда — это сама камера. Вот алгоритм:
Число это расстояние от камеры, в пределах которого мы ожидаем найти объект.
Почему алгоритм работает
Всегда ли алгоритм дойдет до точки пересечения с объектом (точнее, будет стремиться к ней)? Объект может иметь сложную форму и другие ее части могут близко приближаться к лучу, не давая алгоритму сойтись к точке пересечения. На самом деле такого быть не может: другие части объекта обязательно будут на некотором ненулевом расстоянии от луча (иначе он бы их пересекал), которое мы обозначим 0$” data-tex=”inline”/>. Тогда функция SDF будет больше
для любой точки луча (кроме точек, совсем близких к точке пересечения). Поэтому рано или поздно он приблизится к точке пересечения.
С другой стороны, если алгоритм сошелся к некоторой точке, то расстояние между соседними итерациями стремится к нулю SDF (расстояние до ближайшей точки объекта) тоже стремится к нулю
в пределе
алгоритм сходится к точке пересечения луча с объектом.
Получение цвета пикселя по точке пересечения
Представим, что для каждого пикселя мы нашли точку пересечения с объектом. Мы можем нарисовать эти значения (то есть расстояние от камеры до точки пересечения) напрямую и получить такие картинки:
С учетом того, что это было получено при помощи Excel, неплохо. Но хочется узнать, нельзя ли сделать цвета больше похожими на то, как мы видим предметы в жизни.
В компьютерной графике базовым методом вычисления цвета является затенение по Фонгу. По Фонгу, итоговый цвет складывается из трех компонент: фоновой, зеркальной и диффузной. С учетом того, что мы не стремимся к фотореалистичным рендерам, достаточно использовать лишь диффузную компоненту. Формула для этой компоненты следует из закона Ламберта и утверждает, что цвет пикселя пропорционален косинусу угла между нормалью к поверхности и направлением к источнику света.
Далее, для упрощения вычислений, предположим, что источник света и камера совпадают. Тогда нам, по сути, требуется найти синус угла между лучом, исходящим из камеры и поверхностью объекта:
Искомый угол я обозначил одной дугой на чертеже. Значение его синуса обозначено как
.
Обычно, когда используется метод Ray Marching, для нахождения нормали к объекту делают следующее: считают значение SDF в шести точках (несложно уменьшить число точек до четырех) рядом с точкой пересечения и находят градиент этой функции, который должен совпадать с нормалью. Мне показалось, что это слишком много вычислений для Excel, и хотелось бы находить искомый угол проще.
Если смотреть на скорость сходимости алгоритма, можно заметить, что если угол между лучом и предметом прямой, то достаточно одной итерации. Если же угол маленький, то алгоритм будет сходиться очень медленно.
Нельзя ли получить информацию об угле к поверхности исходя из скорости сходимости алгоритма? Если это так, что вообще никаких дополнительных вычислений не потребуется: достаточно проанализировать значения предыдущих итераций.
Нарисуем чертеж. Обозначим и
— точки, полученные на соседних итерациях алгоритма. Предположим, что точки находятся достаточно близко к объекту, что его можно заменить на плоскость, угол с которой мы хотим найти. Пусть
,
— расстояния от точек
и
до плоскости. Тогда, согласно алгоритму, расстояние между
и
равно
.
С другой стороны, если обозначить — точку пересечения луча и фигуры, то
, а
, следовательно
То есть интенсивность пикселя равна единица минус отношение функций SDF соседних итераций!
Описываем простые фигуры
Примеры SDF для сферы, куба и тора:
 | |
 | |
 |
Фигуры можно перемещать и сжимать вдоль осей:
 | |
 |
Фигуры также можно объединять, пересекать и вычитать. То есть SDF поддерживает основные операции конструктивной сплошной геометрии:
 | |
 | |
 |
Внимательный читатель мог заметить, что у некоторых фигур (например, куба), а также для некоторых операций (например, сжатия), приведенные формулы не всегда возвращают расстояние до ближайшей точки объекта, то есть формально не являются SDF. Тем не менее, выяснилось, что их все равно можно подавать на вход движку SDF и он будет их корректно отображать.
Это малая часть того, что можно делать при помощи SDF, полный список фигур и операций можно найти на странице www.iquilezles.org/www/articles/distfunctions/distfunctions.htm
Совмещая все приведенные формулы, получаем первую фигуру:
 |
Формула чайника
С чайником немного сложнее: нужен план
Аккуратно записываем формулу:
И подбираем нужный ракурс. Готово:
Камера
Все, что нам осталось — для данного пикселя на экране найти соответствующий ему луч в пространстве, выходящий из камеры. Если точнее, то надо уметь находить точку этого луча по расстоянию до камеры. То есть нам нужна функция , где
— координаты пикселя, а
— расстояние от начала луча (камеры).
Для удобства вычислений координаты пикселей будут задаваться относительно центра экрана. С учетом того, что экран состоит из строк и
столбцов, мы ожидаем координаты в пределах
Далее необходимо определиться с типом проекции камеры: ортогональная, перспективная или «рыбий глаз». По сложности реализации они примерно одинаковы, но на практике чаще всего используется перспективная, поэтому мы будем использовать ее.
Большей части вычислений в этой главе можно было бы избежать, например, поместив камеру в точку и направив вдоль оси
. Но с учетом того, что фигуры также выровнены вдоль осей, в итоге получился бы не очень интересный ракурс. Так в случае куба мы бы видели его как квадрат.
Чтобы обеспечить возможность поворота камеры, нужно аккуратно провести некоторое количество вычислений с Эйлеровыми углами. Таким образом мы получаем три переменные на входе: угол , угол
и расстояние
. Они определяют как положение, так и направление камеры (камера всегда смотрит в начало координат).
При помощи WolframAlpha находим матрицу поворота:
Если применить ее к вектору , получим координаты камеры (не спрашивайте меня, куда пропал минус):
Последующие вычисления будут специфичны для перспективной проекции. Основной объект — экран (на рисунке он красного цвета, в тексте — курсивом). Это воображаемый прямоугольник на некотором расстоянии перед камерой, имеющий, как можно догадаться, однозначное соответствие с пикселями обычного экрана. Камера фактически просто является точкой с координатами . Лучи, соответствующие пикселям, начинаются в точке камеры и проходят через соответствующую точку экрана.
У экрана нет точного местоположения и размера. Точнее, они зависят от расстояния до камеры: если экран отодвинуть дальше, его потребуется сделать больше. Поэтому условимся, что расстояние от камеры до экрана равно 1. Тогда мы можем вычислить значение вектора , соединяющего точку камеры и центр экрана (он такой же как и у центра камеры, только домноженный не на
, а на
):
Теперь нам надо определить размер экрана. Он зависит от угла обзора камеры, который измеряется в градусах и соответствует тому, что в видеокамерах называется «zoom». Пользователь задает его при помощи переменной (field of view). Так как экран не квадратный, необходимо уточнить, что имеется в виду вертикальный угол обзора.
Итак, чтобы определить высоту экрана, нужно найти основание равнобедренного треугольника с вершинным углом и высотой 1: вспоминая тригонометрию, получаем
. На основании этого можно определить размер одного пикселя на экране:
Далее, применяя матрицу поворота к векторам и
, получаем вектора
и
, задающие горизонтальные и вертикальные направления экрана (для упрощения расчетов они также предварительно домножены на
):
Таким образом у нас теперь есть все компоненты, чтобы найти направление луча, выходящего из камеры и соответствующего пикселю с координатами
Это почти то, что нужно. Только надо учесть, что начало луча находится в точке камеры и что вектор направления нужно нормировать:
Так мы получили искомую функцию , которая возвращает точку луча на расстоянии
от его начала, соответствую пикселю с координатами
.
Excel
Файл Excel, который получается в результате, является книгой, состоящей из >6 листов:
| Лист N | ||
| pixelSize: | =TAN(R!AI1 / 2) / (R!I1 / 2) | |
| =1 / КОРЕНЬ(СТЕПЕНЬ(X!AN + X!X2; 2) + СТЕПЕНЬ(Y!AN; 2) + СТЕПЕНЬ(Z!AN + Z!X2; 2)) | ||
| Лист i1 | ||
| dist0: | =formula(X!I1, Y!I1, Z!I1) | |
| =I1 + formula(X!I1 + X!XN * I1, Y!I1 + Y!XN * I1, Z!I1 + Z!XN * I1) | ||
Тот движок подходит только для рендера лабиринтов и эллипсоидов. Используется одномерный Raycaster, из данных которого вверх и вниз рисуются полосы, создающие иллюзию стен. Но зато там реализована полноценная игровая логика, здесь же целью является только трехмерный движок.