для какой логической операции заполнена данная таблица истинности

Логические выражения и таблица истинности

Логические выражения и таблица истинности

Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.

Логическое выражение — составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения таблицы истинности:

1. подсчитать количество переменных n в логическом выражении;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов: число переменных + число операций;

6. выписать наборы входных переменных;

7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

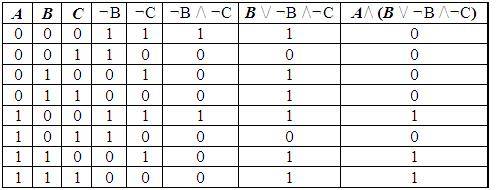
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.

Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.

1. В выражении две переменные А и В (n=2).

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).

5. К_{столбцов}=n+5=2+5=7 столбцов.

Источник

Для какой логической операции заполнена данная таблица истинности

2) Логическое сложение или дизъюнкция:

Таблица истинности для дизъюнкции

3) Логическое отрицание или инверсия:

Таблица истинности для инверсии

4) Логическое следование или импликация:

«A → B» истинно, если из А может следовать B.

Обозначение: F = A → B.

Таблица истинности для импликации

5) Логическая равнозначность или эквивалентность:

Источник

Для какой логической операции заполнена данная таблица истинности

Логическая функция F задаётся выражением (x ≡ ( w ∨ y)) ∨ ((w → z ) ∧ (y → w)).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Рассмотрим данное выражение. Преобразуем логическое выражение (x ≡ ( w ∨ y)) ∨ ((w → z ) ∧ (y → w)) и получим систему, при которой оно ложно:

Заметим, что первый и четвёртый столбцы таблицы истинности это y и w. Из условия следует, что переменная x соответствует второму столбцу таблицы истинности. Следовательно, третьему столбцу соответствует переменная z.

Приведем другое решение.

Составим таблицу истинности для выражения (x ≡ ( w ∨ y)) ∨ ((w → z ) ∧ (y → w)) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные будем записывать в порядке х, y, z, w. Получим следующие наборы: (0, 0, 0, 1), (0, 1, 0, 0), (0, 1, 0, 1), (0, 1, 1, 0).

Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

Первая строка таблицы (как минимум две единицы) может соответствовать либо набору (0, 1, 0, 1), либо набору (0, 1, 1, 0).

Третья строка таблицы также может соответствовать одному из этих двух наборов.

Заметим, что в каждом из этих двух наборах переменная y принимает значение 1, следовательно, ей соответствует первый столбец таблицы.

В данных наборах единичные значения принимают также переменные z и w. Заметим, что переменная z принимает единичное значение в единственном наборе переменных, следовательно, ей не может соответствовать четвертый столбец. Тогда переменной z соответствует третий столбец, а переменной w — четвертый столбец.

Следовательно, переменной х соответствует второй столбец.

Логическая функция F задаётся выражением ((y → x) ≡ (x → w)) ∧ (z ∨ x).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Рассмотрим данное выражение. Преобразуем логическое выражение ((y → x) ≡ (x → w)) ∧ (z ∨ x) и получим систему, при которой оно истинно:

Заметим, что четвёртый столбец таблицы истинности это z, тогда третий столбец таблицы истинности это переменная x. Из условия следует, что переменная y соответствует первому столбцу таблицы истинности, а переменная w соответствует второму столбцу таблицы истинности.

Рассмотрим, как будет выглядеть полная таблица истинности. Одна из переменных z или x должна принимать значение 1, поэтому в третьем столбце в первой строке будет стоять единица, и в четвёртом столбце во второй и третьей строках будут стоять единицы. Исходя из условия можно заключить, что в первом столбце в последней строке будет стоять ноль, а в первой и третьей строках второго столбца будут стоять единицы.

Логическая функция F задаётся выражением ((y → z) ∨ (¬x ∧ w)) ≡ (w ≡ z).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Подберём переменные так, чтобы, выражение было истинно и при этом все переменные кроме одной были равны 0. Такой набор переменных: x = 1, y = 0, z = 0, w = 0. Сопоставляя полученные значения со второй строкой таблицы, получаем, что четвёртая переменная — это переменная x.

Рассмотрим первую строку таблицы. Последовательно рассмотрим случаи, когда y = 1, z = 1, w = 1. В первых двух случаях выражение ложно, а в третьем — истинно, следовательно, вторая переменная — переменная w.

Рассмотрим третью строку таблицы. Заметим, что w = 1, значит, для того, чтобы выражение было истинно z должно быть равно 0. Вторая и четвёртая переменные — w и x, первая переменная равна 0, следовательно, z — первая переменная.

Таким образом, оставшаяся переменная, переменная 3 — это переменная y.

Приведем другое решение.

Составим таблицу истинности функции F и выпишем наборы переменных, при которых функция принимает значение 1. В наборах будем указывать переменные в порядке x, y, z, w. Получим следующие наборы:

(0, 0, 0, 0), (0, 0, 1, 1), (0, 1, 1, 1), (1, 0, 0, 0), (1, 0, 1, 1), (1, 1, 0, 1), (1, 1, 1, 1).

Рассмотрим вторую строку заданной таблицы. Она может соответствовать только набору переменных: x = 1, y = 0, z = 0, w = 0. Тогда четвертый столбец таблицы — это переменная x.

Рассмотрим первую строку заданной таблицы. Заметим, что в первой колонке должна стоять 1, так как наборов переменных, где были бы три нуля, больше нет. Тогда вторая строка может соответствовать только набору x = 0, y = 0, z = 1, w = 1. Следовательно, первая и вторая колонки соответствуют переменным z или w, а третья колонка — это переменная y.

Рассмотрим третью строку таблицы. В ней одна из переменных z или w равна 1, а другая 0. Следовательно, третьей строке может соответствовать только набор переменных x = 1, y = 1, z = 0, w = 1. Тогда первый столбец таблицы — это переменная z, а второй столбец — это переменная w.

Источник

Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.

Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.

Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина

введите функцию или её вектор

Построено таблиц, форм:

Как пользоваться калькулятором

Видеоинструкция к калькулятору

Используемые символы

Для смены порядка выполнения операций используются круглые скобки ().

Обозначения логических операций

Что умеет калькулятор

Что такое булева функция

Что такое таблица истинности?

Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.

Логические операции

Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).

Таблица истинности логических операций

Как задать логическую функцию

Есть множество способов задать булеву функцию:

Рассмотрим некоторые из них:

Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c

Способы представления булевой функции

С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:

Совершенная дизъюнктивная нормальная форма (ДНФ)

Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.

Например, ДНФ является функция ¬a bc ∨ ¬a ¬b c ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.

Совершенная конъюнктивная нормальная форма (КНФ)

Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.

Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.

Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.

Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1

Алгоритм построения СДНФ для булевой функции

Алгоритм построения СКНФ для булевой функции

Алгоритм построения полинома Жегалкина булевой функции

Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.

Примеры построения различных представлений логических функций

Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬a b∨ ¬b c∨ca

1. Построим таблицу истинности для функции

Построение совершенной дизъюнктивной нормальной формы:

Найдём наборы, на которых функция принимает истинное значение: < 0, 0, 1 > < 0, 1, 0 > < 0, 1, 1 > < 1, 0, 1 >

В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:

Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:

Построение совершенной конъюнктивной нормальной формы:

Найдём наборы, на которых функция принимает ложное значение: < 0, 0, 0 > < 1, 0, 0 >

В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:

Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:

Построение полинома Жегалкина:

Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:

Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:

Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:

Окончательно получим такую таблицу:

Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):

Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc

Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.

Источник