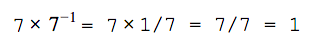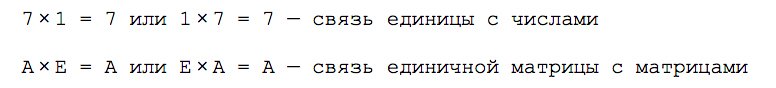для какой матрицы существует обратная к ней

Что такое обратная матрица

Сложная тема из линейной алгебры.

Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:

Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.

С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.

Читать ли эту статью?

❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.

✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.

Обратное — это как?

В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:

Обратные числа при умножении друг на друга всегда дают единицу:

Обратная матрица

В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.

Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:

Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.

Пример квадратной единичной матрицы размером 5×5. Единичная матрица может быть любого размера — состоять из любого количества строк и столбцов

Как рассчитать обратную матрицу

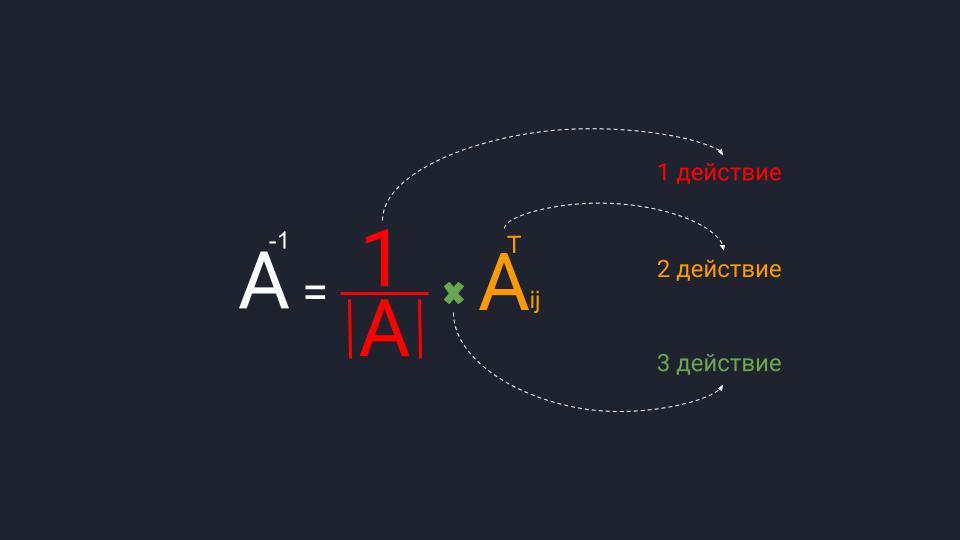
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:

Далее мы по порядку во всём разберёмся.

Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополнений

Определитель — это особое число, которое «определяет» свойства матрицы.

Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.

Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.

Формула для расчёта определителя второго порядка

Пример расчёта определителя второго порядка

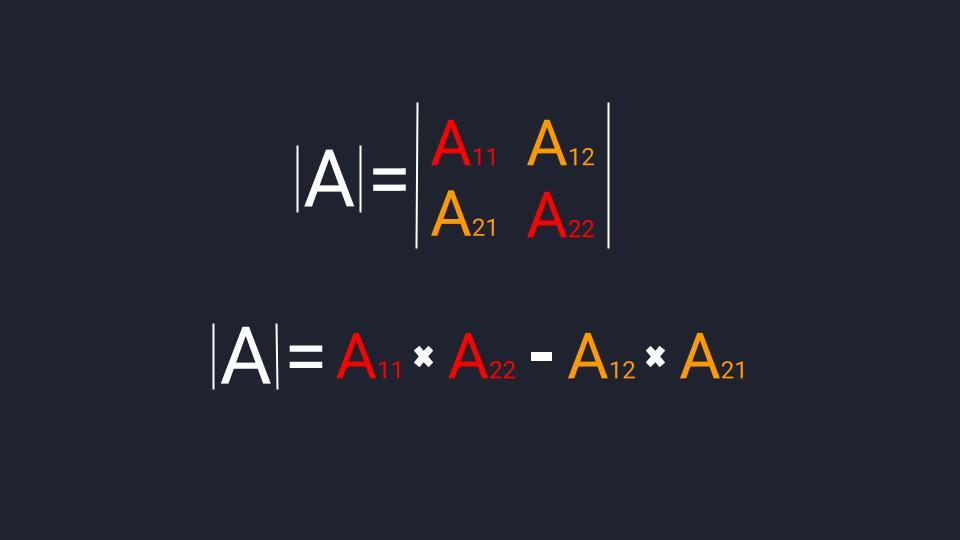
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.

Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.

Считаем определитель третьего порядка: 1-й этап — главная диагональ

Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.

Считаем определитель третьего порядка: 2-й этап — первый треугольник

Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.

Считаем определитель третьего порядка: 3-й этап — второй треугольник

Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.

Считаем определитель третьего порядка: 4-й этап — вторая диагональ

Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.

Считаем определитель третьего порядка: 5-й этап — третий треугольник

Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.

Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник

Общий вид формулы для расчёта определителя третьего порядка

Пример расчёта определителя третьего порядка

Транспонированная матрица алгебраических дополнений вычисляется в три шага:

Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.

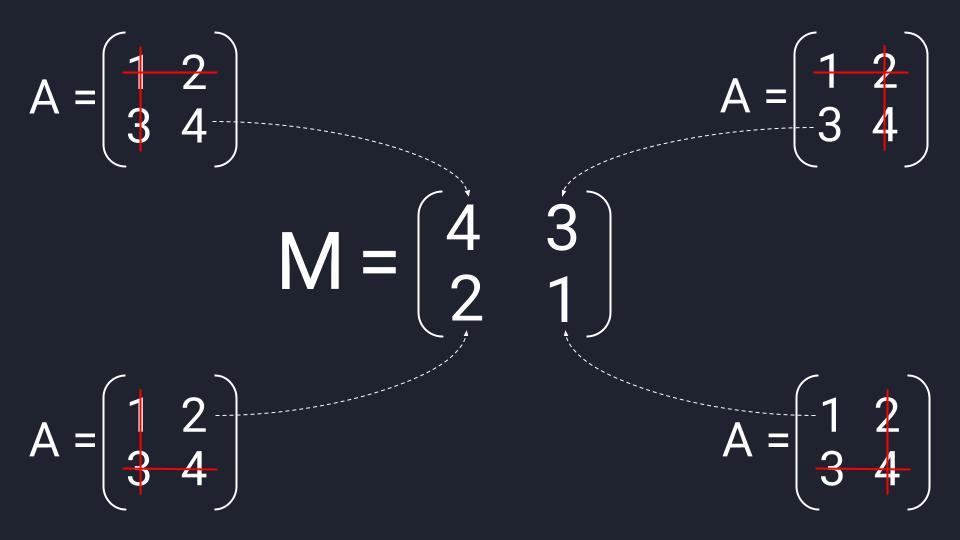
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:

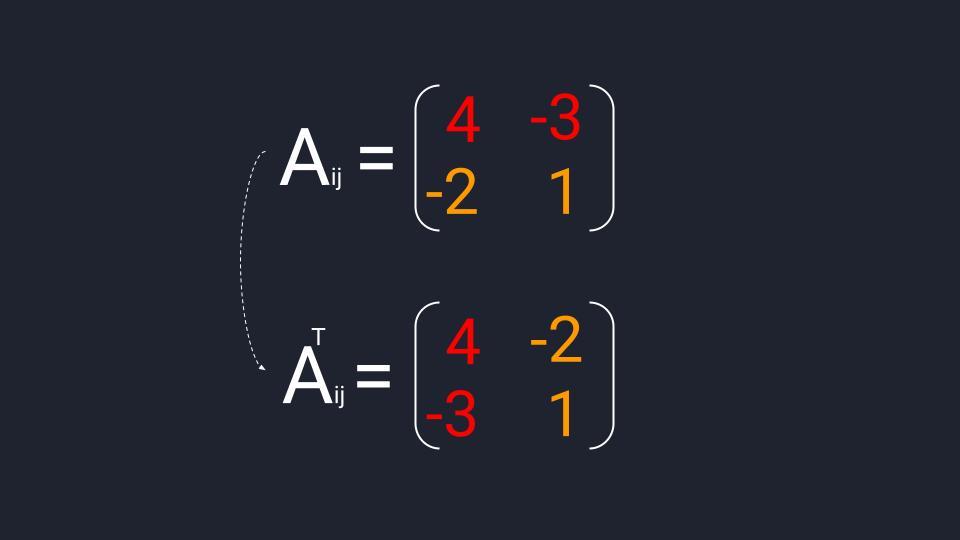
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.

Пример вычисления матрицы миноров из матрицы второго порядка

Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка

Матрица миноров третьего порядка рассчитывается по следующему принципу:

Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:

После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.

Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы

Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.

1-я строка 1-й элемент:

1-я строка 2-й элемент:

1-я строка 3-й элемент:

2-я строка 1-й элемент:

2-я строка 2-й элемент:

2-я строка 3-й элемент:

3-я строка 1-й элемент:

3-я строка 2-й элемент:

3-я строка 3-й элемент:

Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.

Получаем из матрицы третьего порядка матрицу миноров

Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка

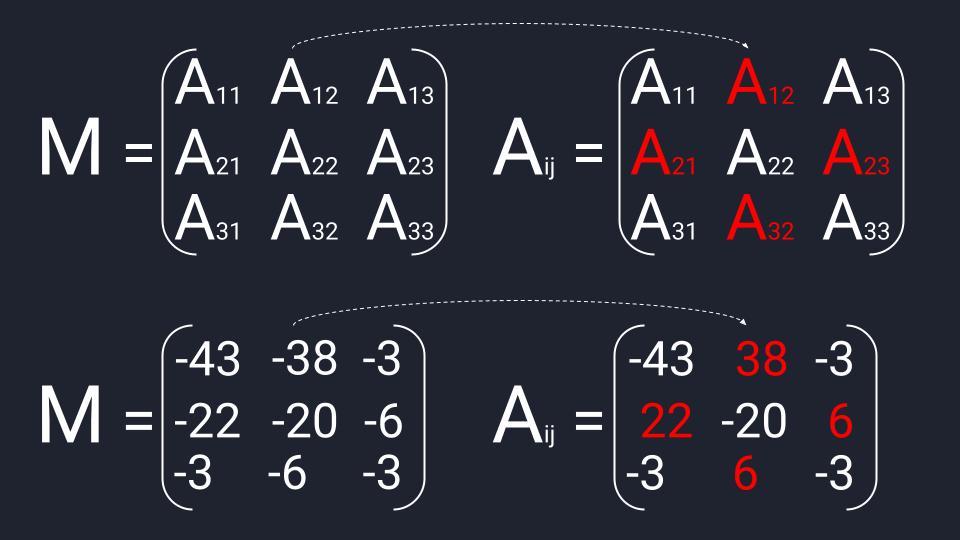
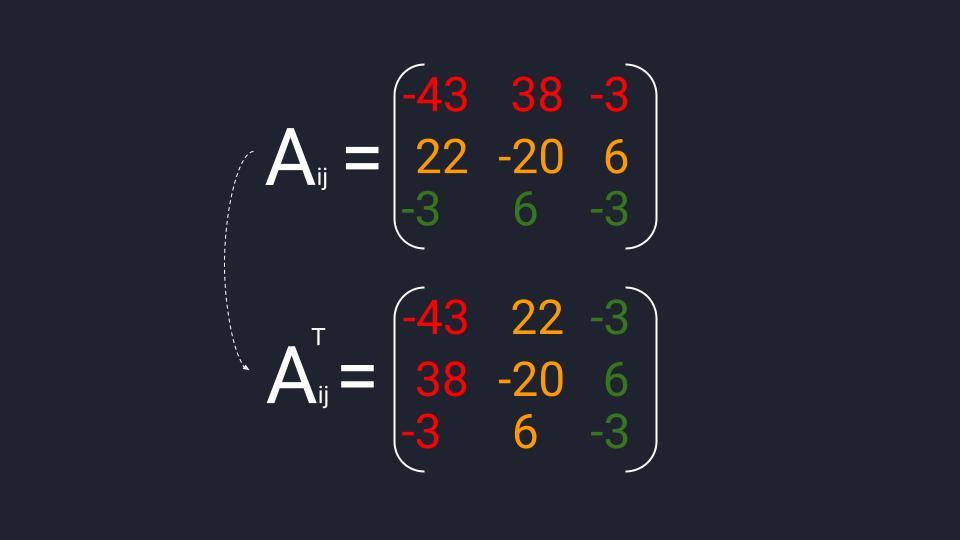
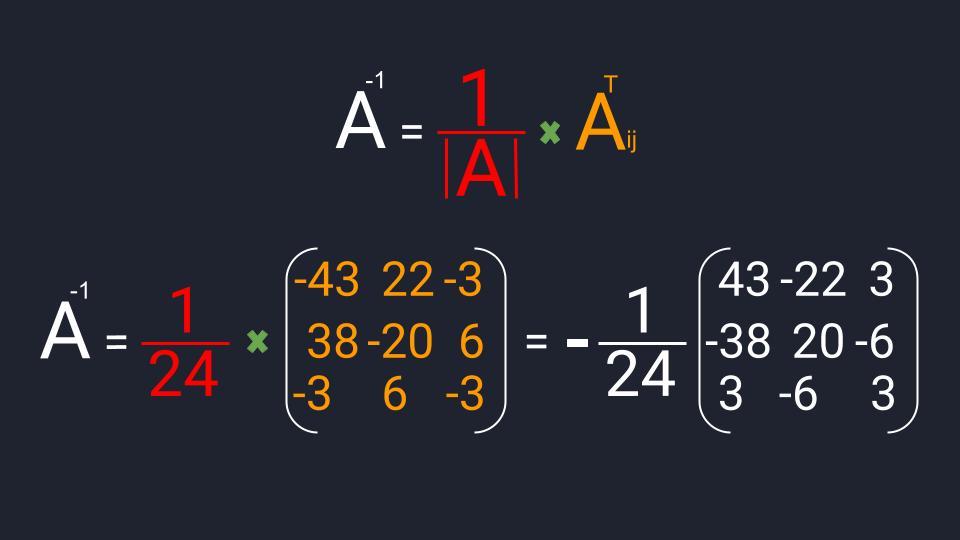
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:

Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось

Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными

Господи, зачем всё это?

Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?

Источник

Обратная матрица и её свойства

Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.

Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.

Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.

Повторение: умножение матриц

Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:

Определение индексов для клеток матрицы

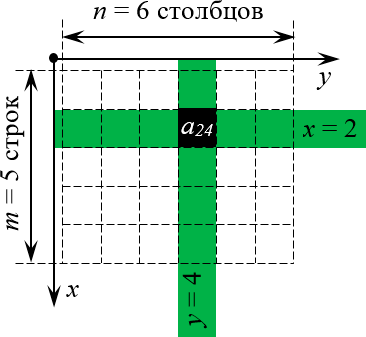
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.

В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.

Умножать можно только согласованные матрицы.

Да, вот такое суровое определение. Из него сразу следует несколько фактов:

Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.

Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)

Что такое обратная матрица

Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.

Ключевое определение

Что ж, пора познать истину.

Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:

Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.

Основные свойства

\[\begin & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end\]

\[\begin & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end\]

\[\begin & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end\]

Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.

Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:

Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.

Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.

Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:

На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.

Но для начала сформулируем «вспомогательное» определение:

Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.

Как найти обратную матрицу

Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.

Алгебраические дополнения

Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».

Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:

Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:

Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)

Что ж, всё это очень мило, но зачем это нужно? А вот зачем.

Основная теорема

А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:

Задача. Найдите обратную матрицу:

\[\left[ \begin 3 & 1 \\ 5 & 2 \\\end \right]\]

Решение. Проверим обратимость. Посчитаем определитель:

\[\left| A \right|=\left| \begin 3 & 1 \\ 5 & 2 \\\end \right|=3\cdot 2-1\cdot 5=6-5=1\]

Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:

Посчитаем алгебраические дополнения:

Итого наша союзная матрица выглядит так:

Осталось посчитать обратную:

Ну вот и всё. Задача решена.

Задача. Найдите обратную матрицу:

Решение. Опять считаем определитель:

Короче, союзная матрица будет выглядеть так:

Следовательно, обратная матрица будет такой:

Ну и всё. Вот и ответ.

Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:

Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.

Альтернативный способ

Элементарные преобразования

Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:

Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.

Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.

Присоединённая матрица

Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.

Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?

В чём прикол? А вот в чём:

\[\left[ A\left| E \right. \right]\to \left[ E\left| B \right. \right]\Rightarrow B=<^<-1>>\]

Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:

Задача. Найдите обратную матрицу:

Решение. Составляем присоединённую матрицу:

Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:

Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.

Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:

Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:

Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:

Осталось лишь поменять местами строки 1 и 3:

Готово! Справа — искомая обратная матрица.

Задача. Найдите обратную матрицу:

Решение. Снова составляем присоединённую:

Немного позалимаем, попечалимся от того, сколько сейчас придётся считать. и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:

Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:

Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:

Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:

И снова слева единичная матрица, значит справа — обратная.:)

Ну вот и всё. Проверку сделайте сами — мне в лом.:)

Источник

Обратная матрица.

Метод обратной матрицы.

Метод обратной матрицы – это один из самых распространенных методов решения матриц и применяется для решения систем линейных алгебраических уравнений (СЛАУ) в случаях, когда число неизвестных соответствует количеству уравнений.

Суть метода обратной матрицы.

Пусть есть система n линейных уравнений с n неизвестными:

Такую систему можно записать как матричное уравнение A* X = B,

где – матрица системы,

– столбец неизвестных,

– столбец свободных коэффициентов.

Обратная матрица к матрице A существует лишь тогда, когда det A ≠ 0. Ввиду этого при решении СЛАУ методом обратной матрицы первым делом находится det A. Если det A ≠ 0, то у системы есть только одно решение, которое можно получить методом обратной матрицы, если же det A = 0, то такая система методом обратной матрицы не решается.

Решение обратной матрицы.

Последовательность действий для решения обратной матрицы:

Приведенный ниже алгоритм решения обратной матрицы по сути такой же, как и приведенный выше, разница только в нескольких шагах: первым делом определяем алгебраические дополнения, а уже после этого вычисляем союзную матрицу C.

Нахождение обратной матрицы.

Нахождение обратной матрицы – это лучше всего делать с помощью присоединённой матрицы.

Теорема: Если к квадратной матрице с правой стороны приписать единичную матрицу такого же порядка и при помощи элементарных преобразований над строками преобразовать начальную матрицу, стоящую слева, в единичную, то полученная с правой стороны будет обратной к начальной.

Пример нахождения обратной матрицы.

Задание. Для матрицы найти обратную методом присоединенной матрицы.

Решение. Дописываем к заданной матрице А справа единичную матрицу 2го порядка:

Из 1й строки вычитаем 2ю:

От второй строки отнимаем 2 первых:

1ю и 2ю строки меняем местами:

От 2й строки отнимаем 2 первых:

Вторую строку умножаем на (-1), а к первой строке добавляем 2ю:

Итак, слева имеем единичную матрицу, а, значит, матрица, которая стоит справа, будет обратной к заданной изначально.

Т.о., имеем .

Ответ после нахождения обратной матрицы:

Замечание. Если на каком-либо этапе в «левой» матрице образуется нулевая строка, значит, что заданная изначально не имеет обратной.

Источник

Для какой матрицы существует обратная к ней

4.1 ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ

.

Легко показать, что

.

Рангом матрицы А (обозначается rang А или r ( A )) является наибольший порядок порожденных ею миноров (определителей), отличных от нуля. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется ее базисным минором. Строки и столбцы, участвующие в образовании базисного минора, также будут базисными. Матрица может иметь несколько базисных миноров, однако все их порядки одинаковы и равны рангу матрицы.

Ранг матрицы не изменится, если:

1) строки и столбцы матрицы поменять местами;

2) переставить местами два любых ее столбца (строки);

3) удалить из нее столбец (строку), все элементы которого равны нулю;

4) удалить из нее столбец (строку), являющийся линейной комбинацией остальных ее столбцов (строк);

5) умножить ее произвольный столбец (строку) на любое отличное от нуля число;

6) к любому ее столбцу (строке) прибавить произвольную линейную комбинацию остальных столбцов (строк) этой матрицы.

Преобразования 2) ‑ 6) называются элементарными. Две матрицы являются эквивалентными, если одна получается из другой с помощью элементарных преобразований и обозначается как А

Для рангов матриц справедливы следующие соотношения:

1) r (A + В ) r(A) + r(B),

3) r (A В ) min<r(A); r(B)>,

5) r ( A В ) = r ( A ), если В – квадратная матрица и D ( В ) 0,

Источник