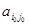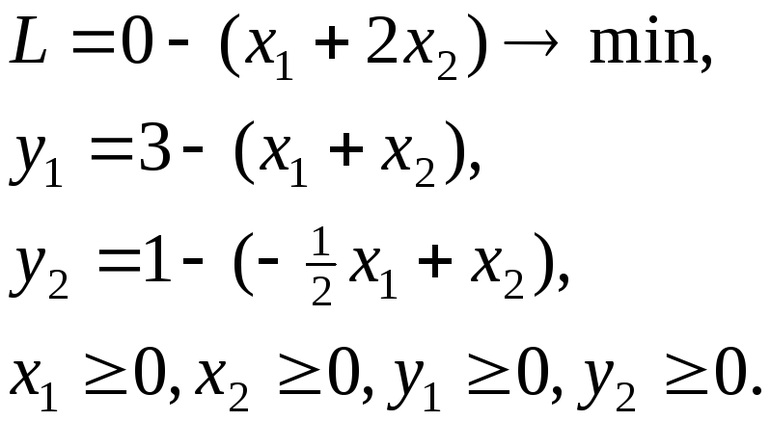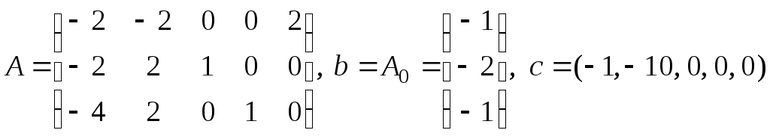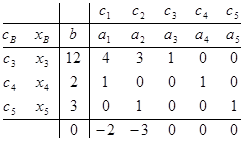для получения базисного решения каким переменным какие значения задаются

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Если система является неопределённой, указать базисное решение.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Источник

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m

Источник

Симплексный метод решения задач линейного программирования

При графическом методе решения задач ЛП мы фактически из множества вершин, принадлежащих границе множества решений системы неравенств, выбрали такую вершину, в которой значение целевой функции достигало максимума (минимума). В случае двух переменных этот метод совершенно нагляден и позволяет быстро находить решение задачи.

Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, трудно представить наглядно область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода или методом последовательных улучшений. Идея метода проста и заключается в следующем.

Рассмотрим симплексный метод на конкретном примере задачи о составлении плана.

Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т. е. имеющих базис, положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.

Рассмотрим задачу о плане производства, предварительно построив модель и приведя ее к специальному виду.

Эта задача имеет специальный вид (с базисом, правые части неотрицательны). Ее можно решить симплекс-методом.

II этап. Проверка опорного плана на оптимальность.

Данной таблице 3.4 соответствует следующий опорный план:

Возможны различные ситуации.

1. В индексной F-строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу, взятому с противоположным знаком. Переходим к IV этапу.

2. В индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция F→∞ неограниченно убывает.

3. В индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к следующему III этапу. пересчитываем таблицу, улучшая опорный план.

III этап. Улучшение опорного плана.

Из отрицательных элементов индексной F-строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим «↑».

Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов только к положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.

Выбрав разрешающий элемент, делаем перечет таблицы по правилам:

1. В новой таблице таких же размеров, что и ранее, переменные разрешающей строки и столбца меняются местами, что соответствует переходу к новому базису. В нашем примере: х₁ входит в базис, вместо х₅, которая выходит из базиса и теперь свободная (табл. 3.6).

2. На месте разрешающего элемента 2 записываем обратное ему число ½.

3. Элементы разрешающей строки делим на разрешающий элемент.

4. Элементы разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком.

5. Чтобы заполнить оставшиеся элементы таблицы 3.6, осуществляем пересчет по правилу прямоугольника. Пусть мы хотим посчитать элемент, стоящий на месте 50.

Соединяем этот элемент мысленно с разрешающим, находим произведение, вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.

Итак, . Записываем 10 на место, где было 50. Аналогично:
, , , .

После пересчета таблицы убеждаемся, что в индексной строке нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.

IVэтап. Выписывание оптимального решения.

— необходимо в план выпуска включить 20 изделий типа А, 40 изделий типа В, при этом прибыль будет максимальной и будет равна 220 руб.

В конце этого параграфа приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, но, возможно, для некоторых читателей будет более удобна в пользовании, т. к. стрелочки указывают четкую направленность действий.

Ссылки над прямоугольниками в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований. правило нахождения первоначального опорного плана будет сформулировано в пункте 3.7.

Условно стандартная задача линейного программирования

Источник

Понятие и алгоритм

Под симплексным методом понимается последовательный переход от одного базисного нахождения системы решений к другому. Эта перестановка повторяется до тех пор, пока переменная величина цели не достигнет своего наибольшего или наименьшего значения. Такой подход является универсальным, его можно использовать для решения любой задачи последовательного программирования.

Метод был разработан в 1947 году математиком из США Бернардом Данцигом. Предложенный способ оказался весьма эффективным для решения задач, связанных с оптимизацией использования ограниченных ресурсов. То есть он позволяет оценить и откорректировать параметры системы, а также получить качественные аналитические результаты.

Существует два подхода решения задачи:

Первый можно использовать для оптимизационного решения двухмерных задач. Например, существует два производственных цикла по сборке ящиков. Выпуск товара характеризуется ограничением в поставках древесины и временем формовки изделия. Для одного необходимо 30 досок, а для другого — 40. Поставщики доставляют в неделю 2 тыс. единиц материала. Первый ящик собирается за 15 минут, а второй — за 30. Нужно определить, какое количество ящиков необходимо производить за неделю на первом конвейере и на втором. При этом первое изделие приносит 10 рублей прибыли, а второе — пять. Время изготовление ограничено 160 часами.

Решение заключается в принятии за Х1 и Х2 количество выпущенных ящиков. Затем — в нахождении максимальной еженедельной прибыли и описании процесса ограничения в виде уравнения.

Это типовая двухмерная задача, условия неотрицательности которой определяются границами прямых: 30*Х1 + 4 0*Х 2 ≤ 2000 (для досок) и 20*Х 1 ≤ 50*Х 2 = 1600 (для сборки). Отложив по оси ординат Х1, а Х2 по абсцисс, и указав на них точки соответствующие уравнениям, можно будет подобрать оптимальное решение для использования сырья и времени.

Графический метод удобно применять для двухмерных задач, но его невозможно использовать при решениях, связанных с размерностью, превышающей три. При этом во всех алгоритмах оптимальный результат принимается допустимым базисному. Симплекс-метод же является вычислительной процедурой, использующей принятое положение, описываемое в алгебраической форме.

Симплекс-метод при базисном решении

Впервые способ был изложен Данцигом в книге «Линейное программирование, его обобщения и применения», изданной на русском языке в 1966 году. Эта теория основывалась на вычислительной процедуре и представлялась в виде стандартных алгебраических форм. Основное направление метода заключается в указании способа нахождения опорного решения, переходе к другому, более оптимальному расчёту и определении критериев, позволяющих остановить перебор опорных вариантов.

Алгоритм решения задачи линейного программирования симплекс методом следующий:

Другими словами, указывается оптимальное опорное решение, способ перехода от одного нахождения ответа к другому, варианты улучшения расчётов. После нахождения первоначального решения с «единичным базисом» вычисляется оценка разложения векторов по базису и заполняется симплексная таблица.

В тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи, используют метод с искусственным базисом. Это симплекс-метод с так называемой М-задачей (ММЭ), решаемый способом добавления к левой части системы уравнений искусственных единичных векторов. При этом новая матрица должна содержать группу единичных линейно-независимых векторов.

Двухфазный способ

Двойственный метод используется при анализе задач линейного программирования, записанного в форме основной задачи. При этом среди векторов, m уравнений, составленных из коэффициентов, должны быть единичные. Такой метод можно использовать, когда свободные члены уравнений являются любыми числами.

Например, существует ограниченность, описываемая функцией:

F = C 1 X 1+ C 2 X 2+…+ CnXn. Используется условие, что Х1Р1+Х2Р2+…+Х(m +1) P (m +1)+ +… XnPn = Р0, где Х j больше либо равно 0 (j =1, n). Принимается, что среди чисел bi (i =1, m) имеются отрицательные.

Решением будет выражение: х= (b1; b2;…; bm ;0;…;0), однако этот ответ не будет разрешать задание, так как к нему могут относиться и отрицательные числа. Так как векторы Р1, Р2… Рм единичные, то каждый из них можно описать линейной областью, состоящей из них же. При этом коэффициентами разложения векторов Рj по области будут числа: Xij = aij (i =1, m; j =1, n) по модулю.

Выражение х= ( b1; b2;…; bm ;0;…;0) определяется базисом. Называют его псевдоплан. Считается, что если дельта j больше либо равна нулю, то для любого: j ( j =1, n ) по модулю. В то же время если в псевдоплане с находимым базисом существует хотя бы одно отрицательное число, то тогда задача вообще не будет иметь планов. Но когда для этих отрицательных чисел верно, что аij меньше нуля, то можно будет перейти к новому псевдоплану.

Объяснение псевдоплана помогает построить алгоритм двойственного метода. Если взять за основу х = (b1; b2;…; bm ;0;…;0) и представить это выражение псевдопланом, то, учитывая исходные данные, можно составить симплекс-таблицу. В ней часть элементов будет отрицательная. Так как дельта j должна быть больше либо равна нулю, то при отсутствии таких чисел в таблице уже будет записан оптимальный план. В обратном случае выбирается по модулю наибольшее из чисел с минусом.

Принцип решения задачи включает следующее:

Если анализ оптимален, считается, что найдено верное решение. В другом случае устанавливается неразрешимость задачи либо составляется новый псевдоплан. Делается это в результате пересчёта табличных данных, например, методом Жордана-Гаусса.

Пример задачи

Использование метода линейного программирования распространено в решениях транспортных задач. Он помогает в целевых расчётах и нужен для минимизации затрат в условиях ограниченной грузоподъёмности и времени обслуживания заказчиков.

Задачи линейного программирования (ЗЛП) позволяют выбрать оптимальную загрузку при перемещении какого-либо товара из одних мест в другие. Во вводных данных указывается число пунктов отправления (м) и количество мест назначения (n). Первые обозначаются как А1, А2…Ам, а вторые – В1, В2…Вn. За аi принимается объём продукции на складе, а bi – потребность. Затраты на перевозку с i пункта в j обозначаются Сij.

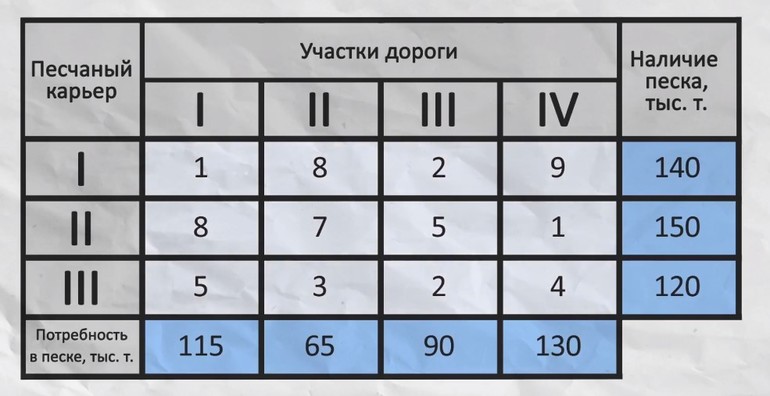
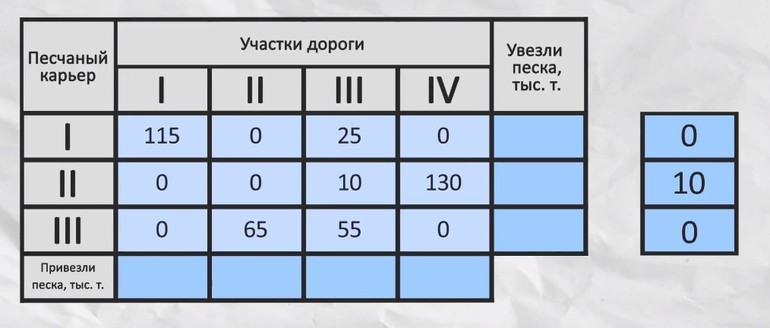
Главная задача — составить план таким образом, чтобы общая стоимость была минимальна. Пусть дано четыре песчаных карьера, с которых необходимо поставить песок на четыре склада. При этом осуществляться перевозки должны за определённую стоимость. Составляем таблицу.

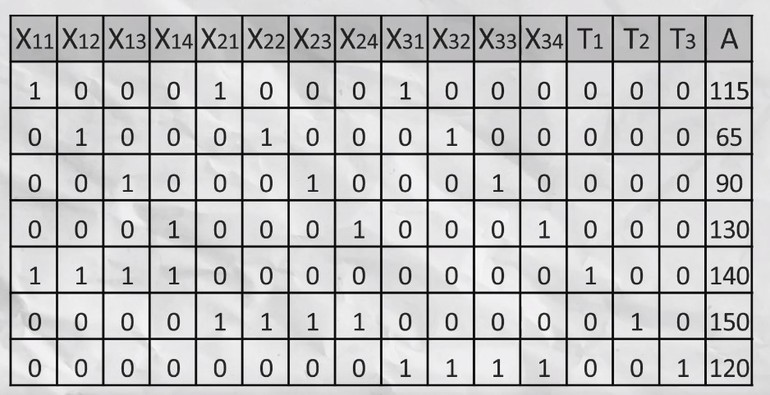
Записываем уравнение ограничения. Сумма всего перевезённого песка с первого карьера должна быть меньше или равна 140. Поэтому можно записать: x11+x12+x12+x14+T1 = 140, где Т1 переменная для хранения остатка. Сумма ограничений будет записана как х11+х21+х31 =115. Аналогичные уравнения составляют и для оставшихся карьеров.

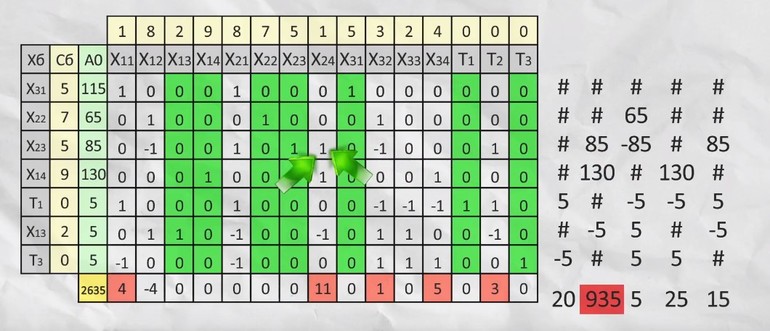
В последней строчке прямоугольника проставляют сумму произведений Сб на этот столбец и вычитают значение суммы перемножения Сб с А0. Делают дополнительное вычисление. Для каждой строки А0 делят на выделенное число, ищут наименьший результат и умножают его на положительные числа из последней строки.

Наибольшее число определяется пересечением ранее выбранных значений, на базе которых создают новый базис. После в соответствии с единичными базисами меняют Сб и Хб. Операцию повторяют до тех пор, пока не исчезнут все положительные числа из последней строки. Заполняют новую таблицу.

Расчёт в Excel

Для включения пакета анализа в программе необходимо перейти в раздел «Параметры» и выбрать строчку «Перейти». В новом окне найти строчку «Пакет анализа», кликнуть по ней и нажать кнопку ОК.

Затем понадобится загрузить и открыть шаблон для проверки в Excel. Используя манипулятор типа «мышь» или клавиатуру, выбрать ячейку G4 и выполнить команду «Сервис/Поиск решения». Далее указать исходные данные, а после нажать кнопку «Выполнить».

Полученное решение можно представить в форме отчёта, содержащего:

Онлайн-сервис для чайников

Метод решения относится к высшей математике, поэтому в нём довольно трудно разобраться даже подготовленному человеку, не говоря уже о чайнике. Существует некоторое количество сайтов с подробным онлайн-решением методом симплекса. На таких сервисах предлагается ввести количество переменных и строк (ограничений). А далее просто заполнить симплекс-таблицу и нажать расчёт. Причём при необходимости вводимые данные можно править, тем самым видеть, как изменяется результат от изменения исходной информации.

Удобным является ещё и то, что обычно на сайтах предлагается создать шаблон решения в Excel или Maple. Решаться любая задача будет почти мгновенно. Подробно можно выполнить расчёт онлайн-калькулятор по методу симплекса на следующих сайтах:

Выполнить расчёт с помощью онлайн-сервисов сможет любой. При этом вероятность ошибки в ответе стремится к нулю. Тем более что для решения задачи даже необязательно знать принцип симплекс-метода.

Источник

Базис и базисное решение

В задаче ЛП базисы и базисные решения играют ключевую роль в организации поиска оптимального решения, если оно существует. С их помощью генерируются очередные вершины области допустимых решений, и организуется переход из одной вершины в другую. Удачный выбор начального базиса и базисного решения может существенно ускорить процесс поиска.

Иллюстрируем возможность такого выбора на примере задачи с ограничениями в виде

Путем разложения А = [B, N] матричное уравнение Ax = b представляется в виде

или что эквивалентно,

Так как по определению матрица B имеет обратную матрицу, решение последнего уравнения относительно вектора х_B, получим в виде

Принимая в этом выражении x_N = 0, получим базисное решение в виде

Если оно неотрицательно, т.е. х_B ≥ 0, получим допустимое базисное решение. Этому решению соответствует вершина множества допустимых решений, которую можно определить в виде

х 1 = 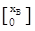. (4.5)

В этой точке значение целевой функции равно f(x 1 ) = c T x 1 = c_B T x_B.

Рассмотрим все три возможности.

Все три вершины являются допустимыми.

1.5. Табличный симплекс-метод (симплекс-алгоритм)

Пусть задача представлена в канонической форме

, (5.1)

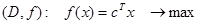
Тогда первая вершина будет равна

(СР)_j = c_j – . (5.4)

Симплекс – разности содержат в себе информацию об оптимальности текущего базисного решения, следовательно, и текущей вершины. Согласно этому правилу, если при решении задачи на максимум на каком-либо шаге (или итерации) симплексных преобразований имеет место

тогда найденное базисное решение является оптимальным. В противном случае поиск решения продолжается.

Легко заметить, что для всех базисных векторов всегда имеет место условие

т. е. векторы из В имеют нулевую симплекс – разность на всех этапах симплексных преобразований.

Пусть необходимо решить задачу

Удобно представить последующие действия в виде последовательности шагов алгоритма. Он состоит из предварительного и основного этапов.

Предварительный этап. Представить задачу в канонической форме

Шаг 1. Разложение матрицы А. Записать ограничения в виде матричного уравнения Ax = b, x ≥ 0, и представить матрицу А в виде

,

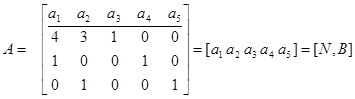
выделив в ней (mxm) – матрицу B полного ранга. Удобно в данном случае выбрать в качестве начального базиса единичную матрицу B = [a₃, a₄, a₅] = I, следовательно, N = [a₁, a₂], I_B <3, 4, 5>, I_N = <1, 2>. Как видно, B = I – единичная матрица размерности (3х3). Если получение базиса В не представляется возможным, то задача не имеет решения.

Шаг 2. Нахождение базисного решения. Начальному базису В соответствует базисное решение в виде

(СР)₁ = c₁ – ,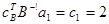

(СР)₂ = c₂ – .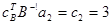

Легко заметить, что из-за нулевого вектора с_В = (0, 0, 0) Т имеет место условие

Шаг 4.Построение и преобразование исходной таблицы Т₀.

Исходная симплекс – таблица, соответствующая решаемой задаче, приведена на рис. 2.2.

Рис. 2.2. Исходная симплекс – таблица.

Шаг 5. Проверка правила остановки

Шаг 6. Выбор направляющего столбца и направляющей строки. Направляющий столбец с индексом j₀ выбирается по наибольшему значению (CP)_j > 0. В нашем случае это (CP)₂ = 3, следовательно, j₀ = 2. Направляющая строка с индексом i₀ выбирается по правилу

.

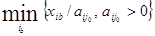
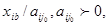
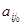
Согласно этому правилу, среди всех отношений типа где x_ib – базисные переменные (их численные значения содержатся в столбце b), — положительные элементы направляющего столбца, выбирается наименьшее отношение с индексом i₀. В нашем случае – это строка с индексом i₀ = 5. Если в направляющем столбце положительных элементов нет, задача не имеет решения из-за неограниченности целевой функции.

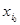
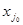
Выбору направляющей строки и направляющего столбца с индексами i₀ и j₀ соответственно соответствует исключение из базисного решения переменной и включение вместо нее переменную , причем, новой переменной в базисе присваивается значение

l₀ = .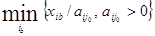

В текущей таблице элемент называется ведущим элементом и отмечается кружком.

Источник