дробь в какую сторону
Сокращение обыкновенных дробей
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:


где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.

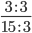
Сокращение выполнено: 
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.

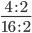
Сокращение выполнено: 
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
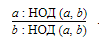
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1

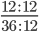
Сокращение выполнено: 
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3

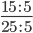
Сокращение выполнено: 
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.

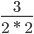
Сокращение выполнено: 
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9

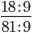
Сокращение выполнено: 
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:

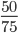
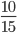
Сокращение выполнено: 
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

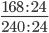
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

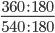
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

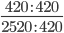
Сокращение выполнено. Дробь приведена к несократимому виду: 
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

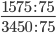
Сокращение выполнено. Дробь приведена к несократимому виду: 
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Как написать дробь на клавиатуре: все способы
Если вы заняты написанием курсовой работы или документа с расчетной частью, вам может потребоваться графический символ, который отсутствует на клавиатуре. Это может быть значок иностранной валюты, символ функции или же математическая дробь. Рассмотрим последний случай. Существует несколько способов написания дроби на клавиатуре.
Вид №1: вертикальная дробь
Предположим, вы хотите изобразить дробь с горизонтальной чертой, которая называется винкулум. Пожалуй, это наиболее привычный для многих из нас вариант, ведь именно так учат записывать дроби школьные учителя математики, и именно это выражение встречается во многих технических, научных и образовательных текстах. В случае «многоэтажных» дробей вам нужно прибегнуть к безграничным возможностям Word.
 Способ 1.
Способ 1.
 Способ 2.
Способ 2.
Стоит учесть, что написание дробей в вертикальном виде отображается далеко не везде. Например, если вы скопируете вертикальную дробь из Word в чат социальных сетей или диалоговое окно Skype, то она отобразится в горизонтальном виде.
Вид №2: солидус
Вариант, часто встречающийся в научных работах, статьях и учебниках, — это дроби с наклонной чертой, которая в математическом мире называется «солидус». Эта дробная черта наклонена вправо приблизительно на 45°, а между цифрами существует специальный интервал (кернинг). Не путайте солидус с обычной косой чертой – они выглядят по-разному!
Изобразить дробь в таком виде можно при помощи Word. Используйте принцип действий, указанный в пункте «Вид №1», только во вкладке «Дробь» выберите вариант «диагональная простая дробь».
Ввести дробь в таком виде можно также через «Microsoft Equation 3.0».
Вид №3: горизонтальная дробь
Более привычный для нас вариант, который часто встречается в публицистических и научно-популярных статьях – это горизонтальная дробь.
Горизонтальную дробь можно ввести четырьмя способами:
Самый простой и быстрый способ изобразить дроби, не прибегая к вставкам – использовать «слэш» (или косую черту, наклоненную вправо) на клавиатуре. Именно так поступает большинство пользователей Интернета, которые не желают тратить время на поиск нужных символов. Конечно же, для тех, кто занят написанием серьезных научных работ, лучше выбрать специальные изображения дробей.
Слэш располагается на клавиатуре в следующих местах:
Вы также можете набрать слэш следующим образом:
Чтобы дробь, записанная через слэш, смотрелась естественнее, можно использовать следующую последовательность:
Теперь вы знаете, как написать дробь на клавиатуре. Как видите, это можно сделать самыми разными способами, и каждый из них достаточно прост. Желаем вам успехов в дальнейшем освоении компьютерной грамоты!
Значение слова «дробь»
2. перен.; чего или какая. Частые повторяющиеся звуки, возникающие от ударов по чему-л. Впереди шел взвод солдат, и четыре барабанщика отбивали суровую, мерную дробь. Короленко, История моего современника. Из комнаты доносилась сухая дробь пишущих машинок. Шолохов, Тихий Дон.
3. (род. мн. дробе́й). Мат. Число, состоящее из частей единицы. Простые дроби. Десятичные дроби. Правильная дробь. Неправильная дробь.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Быстрые, частые, отрывистые звуки. Например, барабанная дробь. (см. барабанный рудимент)
На флоте, команда «дробь!» — прекращение огня.
«Барабанная дробь» (англ. The Sound of Drums) — эпизод британского научно-фантастического сериала «Доктор Кто».
ДРОБЬ, и, ж. 1. только ед., собир. Мелкие свинцовые шарики (употр. для стрельбы из охотничьего ружья). В утку попал весь заряд дроби. 2. Число, состоящее из частей единицы (мат.). Правильная д. (меньше единицы). Неправильная дробь (больше единицы). Десятичные дроби. Непрерывная д. 3. только ед. Разбитые, измельченные части чего-н. (спец.). В стекле много дроби. 4. перен., только ед. Ряд частых, прерывистых звуков, трель. Соловей. мелкой дробью вдруг по рощам рассыпа́лся. Крлв. Барабанная д.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
дробь
1. собир. мелкие свинцовые шарики, употребляемые обычно для стрельбы из охотничьего ружья ◆ Мы выпалили из ружья дробью поверх голов их, они все испугались, женщины и некоторые из молодых людей отступили подалее в лес, а прочие все присели. Ф. Ф. Беллинсгаузен, «Двукратные изыскания в Южном Ледовитом океане и плавание вокруг света в продолжение 1819, 20 и 21 годов, совершённые на шлюпах «Востоке» и «Мирном» под начальством капитана Беллинсгаузена командира шлюпа «Восток», шлюпом «Мирным» начальствовал лейтенант Лазарев», 1831 г. (цитата из НКРЯ)
2. матем. число, состоящее из долей единицы, нецелое число ◆ Мы присвоили последней дроби знак минус, ибо каждая из первых дробей отрицательна, вследствие того что положительно K. М. В. Остроградский, «Общие соображения относительно моментов сил», 1834 г. (цитата из НКРЯ) ◆ Было уже ему без малого пятнадцать лет, когда перешёл он во второй класс, где, вместо сокращённого катехизиса и четырёх правил арифметики, принялся он за пространный, за книгу о должностях человека и за дроби. Н. В. Гоголь, «Иван Фёдорович Шпонька и его тётушка», 1831—1832 г. ◆ Число, на которое здесь умножается r, может быть найдено только чрез приближение в десятичных дробях, его обыкновенно означают в математических книгах π, так, что величина дуги 200° будет выражаться πr. Н. И. Лобачевский, «Геометрия», 1823 г. (цитата из НКРЯ)
3. частые повторяющиеся звуки, похожие на звуки рассыпающихся шариков (трель, щелкотня, бой) ◆ Бывало, как пустит дробь языком — ну соловей, точно соловей! А. А. Бестужев-Марлинский, «Мулла-Нур», 1836 г. (цитата из НКРЯ) ◆ Выстрелы, говорит один свидетель, сыпались подобно дроби, битой десятью барабанщиками. А. С. Пушкин, «История Пугачёва», 1833 г. ◆ Пошли, тронулись, барабан рассыпается частой дробью, идём… А. А. Бестужев-Марлинский, «Письма из Дагестана», 1831 г. (цитата из НКРЯ) ◆ Овины курились за полночь, стук цепов унылою дробью разносился по всей окрестности. М. Е. Салтыков-Щедрин, «Господа Головлёвы», 1875—1880 г.
4. морск. устар. военн. сигнал на горне или барабане, приказывающий прекратить огонь (стрельбу), а также команда о прекращении огня ◆ § 67. Во всяком случае, когда обучающий захочет окончить пальбу, то приказывает барабанщику ударить дробь. Что повторяют немедленно все барабанщики во фронте. § 68. По дроби солдаты перестают стрелять; всякий, зарядив ружьё, берёт оное наизготовку и дожидает команды. «Воинский устав о пехотной службе. Часть 1. О строевой службе.», 1811 г. ◆ На стрельбу, как правило, отводится 12 залпов, после расхода боеприпасов даётся команда: «Дробь!» и принимается доклад от командиров орудий: «Канал ствола чист!». Юрий Леонидович Кручинин, «Командую кораблём», 2010 г.
5. то же, что косая черта, типографский знак, используемый для обозначения операции деления ◆ А при некоторой поддержке дом «шесть дробь один» сумеет продержаться долго и тем расстроить немецкую программу. Василий Гроссман, «Жизнь и судьба», 1960 г. (цитата из НКРЯ) ◆ В рамках дня памяти жертв сталинских репрессий и объявленного Советом Европы года преодоления коммунизма рассматривается дело Р-788, приговор Военной коллегии 4н-012045 дробь 55 по убийству Уманской Нины Константиновны. Александр Терехов, «Каменный мост», 1997-2008 г. (цитата из НКРЯ)

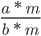
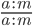
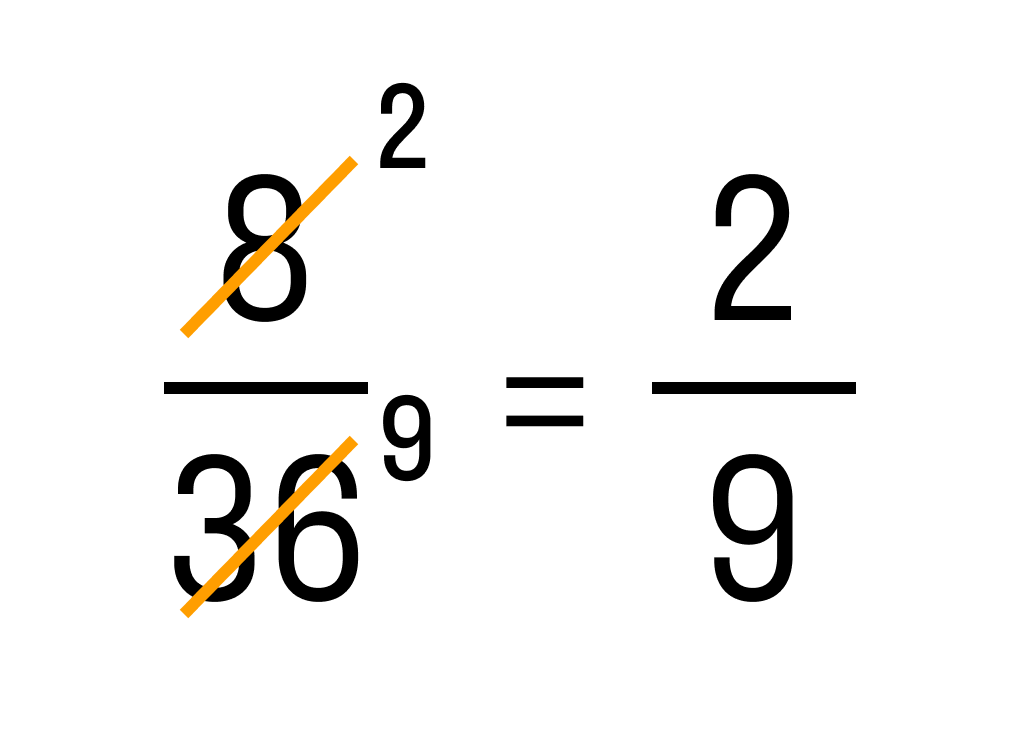
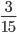
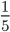
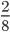
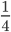
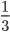
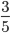
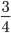
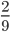
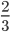
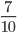
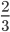
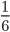
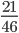
 Способ 1.
Способ 1. Способ 2.
Способ 2.






