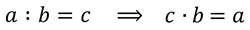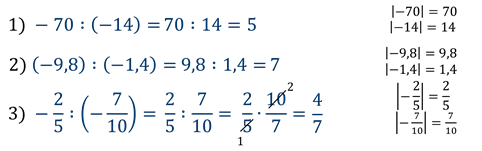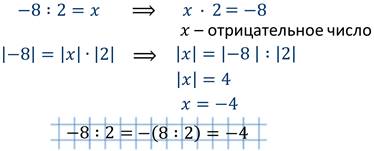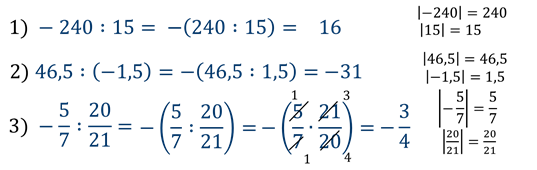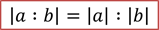если отрицательное число разделить на отрицательное число какое число получится
Почему минус на минус всегда даёт плюс?
Польза натуральных чисел
Для начала немного окунёмся в историю арифметики. Совершенно естественно, что в самом начале люди пользовались только натуральными числами — один, два, три и так далее. Их использовали для того, чтобы посчитать реальное количество предметов. Просто так, в отрыве от всего, цифры были бесполезны, поэтому стали появляться и действия, с помощью которых стало возможно оперировать числами. Абсолютно логично, что самым необходимым для человека стало сложение. Эта операция проста и естественна — подсчитать количество предметов становилось проще, теперь не нужно было каждый раз считать заново — «один, два, три». Заменить счёт теперь стало возможным с помощью действия «один плюс два равно три». Натуральные числа складывались, ответ тоже был натуральным числом.
Умножение представляло собой, по сути, такое же сложение. На практике мы и сейчас, например, совершая покупки, так же используем сложение и умножение, как это делали давным-давно наши предки. Однако порой приходилось совершать операции вычитания и деления. И числа не всегда были равнозначны — иногда число, от которого отнимали, было меньше числа, которое вычитали. То же и с делением. Таким образом и появились дробные числа.
Появление отрицательных чисел
В документах Индии записи об отрицательных числах появились в VII веке нашей эры. В китайских документах существуют более древние отметки об этом математическом «факте».
В жизни мы чаще всего отнимаем от большего числа меньшее. Например: у меня есть 100 рублей, хлеб и молоко стоят 65 рублей; 100 — 65 = 35 рублей сдачи. Если же я захочу купить ещё какой-то товар, стоимость которого превышает мои оставшиеся 35 рублей, например ещё одно молоко, то как бы я ни хотел его приобрести, а больше денег у меня нет, следовательно, отрицательные числа мне ни к чему.
Практически для таких же целей и начали впервые использовать отрицательные числа. Китайцы первыми использовали их для записи долгов или в промежуточных решениях уравнений. Но использование это было всё равно лишь для того, чтоб прийти к положительному числу (впрочем, как и наше погашение кредитки). Долгому отвержению отрицательных чисел способствовало то, что они не выражали конкретных предметов. Десять монет — это десять монет, вот они, их можно потрогать, на них можно купить товар. А что значит «минус десять монет»? Они предполагаются, даже если это долг. Неизвестно, вернётся ли этот долг, и превратятся ли «записанные» монеты в реальные. Если при решении какой-нибудь задачи получалось отрицательное число, считалось, что вышел неверный ответ или ответа вообще не существует. Такое недоверчивое отношение сохранялось у людей достаточно долго, даже Декарт (XVII век), совершивший прорыв в математике, считал отрицательные числа «ложными».
Формирование правил действий с отрицательными числами
Рассмотрим уравнение 9х-12=4х-2. Для решения уравнения нужно перенести члены с неизвестным в одну сторону, а известные числа — в другую. Это можно выполнить двумя способами.
Переносим часть уравнения с неизвестным в левую сторону, а другие числа — в правую. Получается:
Ответ найден. За все действия, что нам потребовалось выполнить, мы ни разу не прибегнули к использованию отрицательных чисел.
Теперь переносим часть уравнения с неизвестным в правую сторону, а остальные слагаемые — в левую. Получаем:
Чтобы найти решение, нам нужно одно отрицательное число разделить на другое. Однако верный ответ мы уже получили в предыдущем решении — это х, равное двум. Следовательно, остаётся вывести, что (-10)/(-5)=2.
Что доказывают нам эти два способа решения одного уравнения? Первое, что становится ясно – это то, каким образом выводилась адекватность оперирования отрицательными числами — полученный ответ должен быть таким же, что и при решении с использованием только натуральных чисел. Второй момент — это тот факт, что не нужно больше задумываться над величинами, чтобы получать непременно неотрицательное число. Можно выбирать наиболее удобный способ решения, особенно это касается сложных уравнений. Действия, которые позволили не задумываться над некоторыми операциями (что нужно сделать, чтоб были только натуральные числа; какое число больше, чтоб вычитать именно от него и т.д.), стали первыми шагами к «абстракцианизации» математики.
Естественно, не все правила действий с отрицательными числами сформировались единовременно. Копились решения, обобщались примеры, на основе чего и стали понемногу «вырисовывать» основные аксиомы. С развитием математики, с выделением новых правил, появлялись новые уровни абстракции. Например, в девятнадцатом веке стало доказано, что целые числа и многочлены имеют много общего, хотя внешне отличаются. Все их можно складывать, вычитать и перемножать. Правила, которым они подчиняются, влияют на них одним образом. Что же касается деления одних целых чисел на другие, то здесь «поджидает» занимательный факт — ответом не всегда будет целое число. Этот же закон распространяется и на многочлены.
Затем было выявлено множество других совокупностей математических объектов, над которыми возможно было производить такие операции: формальные степенные ряды, непрерывные функции. Со временем математики установили, что после исследования свойств операций результаты станет возможно применять ко всем этим совокупностям объектов. Точно так же работают и в современной математике.
Больше интересных материалов:
Сугубо математический подход
С течением времени математики выявили новый термин — кольцо. Под кольцом подразумевают множество элементов и операции, которые можно над ними производить. Основополагающими становятся правила (те самые аксиомы), которым подчиняются действия, а не природа элементов множества. Для того, чтоб выделить первостепенность структуры, возникающую после введения аксиом, как раз обычно и употребляют термин «кольцо»: кольцо целых чисел, кольцо многочленов и т. п. Используя аксиомы и исходя из них, можно выявлять новые свойства колец.
Сформулируем правила кольца, похожие на аксиомы операций с целыми числами, и докажем, что в любом кольце при умножении минуса на минус выходит плюс.
Под кольцом понимается множество с двумя бинарными операциями (в каждом действии участвуют два элемента кольца), традиционно именуемыми сложением и умножением, и следующими аксиомами:
— сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (—A)), что A + (—A) = 0;
— умножение подчиняется сочетательному закону: A · (B · C) = (A · B) · C;
— сложение и умножение связаны следующими правилами раскрытия скобок:
(A + B) · C = A · C + B · C
A · (B + C) = A · B + A · C.
Уточним, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (операция деления не всегда возможна), ни существования единицы — нейтрального элемента по умножению. Если ввести данные аксиомы, получим другие алгебраические структуры, однако со всеми действующими теоремами, доказанными для колец.
Из этого получим утверждения про единицы:
Далее следует доказать некоторые моменты. Во-первых, нужно установить существование лишь одной противоположности для каждого элемента. Допустим, наличие у элемента А два противоположных элемента: B и С. То есть A + B = 0 = A + C. Разберём сумму A + B + C. Используя переместительный и сочетательный законы, а также свойства нуля, получим, что сумма равна:
B: B = B + 0 = B + (A + C) = A + B + C
C: A + B + C = (A + B) + C = 0 + C = C.
Следовательно, B = C.
Отметим, что и A, и (-(-A)) противоположны к элементу (-A). Отсюда заключаем, что элементы A и (-(-A)) должны быть равны.
Далее, 0 = 0 · B = (A + (-A)) · B = A · B + (-A) · B,
Заметим, что 0 · B = 0 для любого элемента B.
0·B = (0 + 0) B = 0·B + 0·B,
таким образом, прибавление 0·B не изменяет сумму. Получается, это произведение равно нулю.
Урок 37 Бесплатно Деление
В прошлом уроке мы познакомились с умножением.
Сейчас перейдем к делению, узнаем правила деления для чисел с разными знаками, деления отрицательных чисел, проведем параллели между умножением и делением, а также определим, какой может быть знак результата деления в зависимости от знаков делимого и делителя.
Деление отрицательных чисел
Правило: для того, чтобы разделить одно отрицательное число на другое отрицательное число, необходимо разделить модуль первого числа на модуль второго числа.
Это правило очень похоже на правило для умножения. Откуда такая схожесть мы узнаем чуть позже, а пока посмотрим на примеры.
Пример:
Допустим надо разделить -15 на -5
1) Найдем модули от этих чисел:
2) Посчитаем частное этих двух чисел:
Пример:
Разделим -132 на -3
1) Находим модули этих чисел:
2) Посчитаем частное модулей:
Это правило работает для нецелых чисел:
2) Выполняем деление:
И еще несколько примеров уже менее подробно:
Пройти тест и получить оценку можно после входа или регистрации
Деление чисел с разными знаками
Допустим, мы знаем, что на заводе 250 работников, получающих одинаковую зарплату, также мы знаем, что вся сумма денег на выплату зарплат изменилась на -100000 рублей.
На сколько изменилась зарплата каждого конкретного работника?
Необходимо разделить общее изменение на количество работников. Иными словами, необходимо разделить отрицательное число на положительное.
Правило: чтобы разделить отрицательное число на число положительное, нужно поделить модуль первого числа на модуль второго числа и к результату деления приписать минус.
Воспользуемся им для решения задачи:
1) Берем модули чисел:
3) И приписываем к результату минус:
Получаем, что зарплата каждого работника изменилась на -400 рублей, иными словами, уменьшилась на 400 рублей.
Теперь посмотрим, как разделить положительное число на отрицательное.
Правило: чтобы разделить положительное число на число отрицательное, нужно поделить модуль первого числа на модуль второго числа и к результату приписать минус.
Допустим, необходимо разделить 161 на -7:
1) Посчитаем модули:
2) Посчитаем частное:
3) И приписываем к нему минус:
Это и будет ответом.
Заметим, что оба правила достаточно похожи, поэтому можно их обобщить и запомнить общее правило.
Правило: чтобы посчитать частное чисел с разными знаками, необходимо посчитать частное их модулей и приписать к нему минус.
Пройти тест и получить оценку можно после входа или регистрации
Сведение деления к умножению
Вы уже могли заметить, что правила для умножения и деления весьма похожи. Это вполне закономерно.
Как мы уже говорили в уроке про деление дробей, деление можно заменить умножением делимого на число, обратное делителю.
И это верно для отрицательных чисел тоже.
Посмотрим, как это происходит на примерах.
1-й способ: воспользоваться правилом для деления отрицательных чисел:
2-й способ: представить деление как умножение на число, обратное делителю, и воспользоваться правилом для умножения отрицательных чисел:
Как вы можете заметить, результаты вычислений разными подходами совпадают. Более того, совпадают даже последние действия, поэтому можете выбирать любой удобный для вас способ.
Такой же подход работает и для деления чисел с разными знаками.
Пример:
1-й способ: воспользуемся правилом для деления чисел с разными знаками:
2-й способ: заменим деление на умножение и воспользуемся правилом для умножения чисел с разными знаками:
Можно заметить, что результаты совпадают.
Так что можно выбирать любой способ для выполнения деления чисел с разными знаками.
Пройти тест и получить оценку можно после входа или регистрации
Определение знака частного
Если мы хотим определить, какой знак будет у частного, не считая его, тогда нам помогут следующие правила:
Правило: частное двух отрицательных чисел всегда число положительное
Пример:
Частное \(\mathbf<-32>\) и \(\mathbf<-4>\) будет больше нуля.
Правило: частное положительного числа и отрицательного равно нулю
Пример 1:
Частное 45 и \(\mathbf<-5>\) будет меньше нуля.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Мы уже говорили о площади круга и площади квадрата.
Эти знания нам сейчас пригодятся, потому что так мы можем найти математическую ошибку в одном литературном произведении, а именно, в романе Джека Лондона «Маленькая хозяйка большого дома».
«Посреди поля возвышался стальной шест, врытый глубоко в землю. С верхушки шеста к краю поля тянулся трос, прикреплённый к трактору. Механики нажали рычаг, и мотор заработал.
Машина сама двинулась вперёд, описывая окружность вокруг шеста, служившего его центром.
– Чтобы окончательно усовершенствовать машину, Грэхем, вам остаётся превратить окружность, которую она описывает, в квадрат.
– Да, на квадратном поле пропадает при такой системе очень много земли.
Грэхем произвёл некоторые вычисления, затем заметил:
– Теряем примерно три акра из каждых десяти.
И сейчас мы проверим, прав ли был Грэхем.
Посчитаем площадь квадрата: возводим длину сторон х в квадрат.
Так что площадь квадрата- \(\mathbf
Теперь посчитаем площадь круга: \(\mathbf<\pi(\frac
Теперь мы можем вычесть из площади квадрата площадь круга и понять, какая часть площади не используется.
Как мы видим, не используется 0.22 земли, что явно меньше 0.3, о которых говорится в тексте.
Возможно, так автор хотел изобразить математическое невежество героев, или же он просто не уделил внимание таким подробностям.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Деление
Урок 37. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Деление»
Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел. Напомним, что деление – это действие, обратное умножению.
Как известно, разделить число на а на число b – это значит найти такое число с, которое при умножении на b даёт а.
Разделим число –8 на число –2. Т.е. надо найти такое число х, которое при умножении на –2 даст число –8.
Чтобы разделить отрицательное число на отрицательное, нужно модуль делимого разделить на модуль делителя.
Запомните! Частное двух отрицательных чисел – это положительное число.
Делить отрицательные числа мы научились. Рассуждая аналогичным образом, давайте разберёмся, как делят числа с разными знаками.
Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «минус».
Обратите внимание, что не имеет значение перед делимым или делителем стоит знак «минус». Частное двух чисел с разными знаками – это отрицательное число.
Вам хорошо известны свойства числа 1, записанные следующими формулами:
Эти свойства сохраняются и когда а – отрицательное число. Убедимся в этом.
Если делимое равно 0, а делитель – любое число, отличное от 0, то частное равно 0.
Не забывайте, что на 0 делить нельзя!
Модуль частного двух чисел равен частному их модулей.
А знак частного зависит от знаков делимого и делителя: если делимое и делитель имеют одинаковые знаки (т.е. оба положительны или оба отрицательны), то частное положительно, а если разные – отрицательно.
Рассмотрим таблицу, которая наглядно показывает зависимость знака частного от знаков делимого и делителя:
Запомнить эту таблицу очень легко. Смотрите, при делении чисел с одинаковыми знаками получается положительное число, а при делении чисел с разными знаками – отрицательное.
Упражнение: определите знак произведения и частного.
Чтобы разделить отрицательное число на отрицательное, нужно модуль делимого разделить на модуль делителя.
Частное двух отрицательных чисел – это положительное число.
Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «минус».
Частное двух чисел с разными знаками – это отрицательное число.
Остаток от деления отрицательных чисел
В этой статье я расскажу о том, как правильно находить остаток от деления отрицательных чисел. Этой теме, к сожалению, уделяется очень мало внимания в школе, хотя для понимания учеником базовых основ математики она чрезвычайно важна. Именно поэтому, как репетитор по математике, на своих занятиях я разбираю это материал с учениками во всех подробностях. Это значительно упрощает дальнейшую подготовку к ЕГЭ, ОГЭ, вступительным экзаменам и олимпиадам по математике.
Итак, приступим. Чтобы разделить друг на друга два целых числа с остатком, нужно воспользоваться следующей теоремой:
Для любых целых чисел 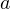 и и 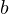 , причём , причём 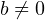 , найдётся единственная пара целых чисел , найдётся единственная пара целых чисел 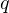 и и  , таких что , таких что 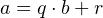 , где , где 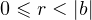 . . |
Здесь 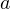
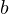
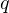


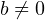
Звучит довольно сложно, но на самом деле в этой теореме нет ничего сложного. Чтобы во всём разобраться, перейдём к примерам.
Примеры нахождения остатка от деления отрицательных чисел
Пример 1. Деление с остатком положительного целого числа на положительное целое число.
Допустим, что требуется разделить с остатком 27 на 4. Вопрос состоит в том, сколько раз число 4 содержится в числе 27? Но мы знаем, что нет такого целого числа, на которое можно умножить 4, чтобы получить 27. Поэтому вопрос нужно переформулировать. На какое число нужно умножить 4, чтобы получить число, максимально близкое к 27, но не превзойти его? Очевидно, что это число 6. Если 4 умножить на 6, то получится 24. До исходного делимого 27 не хватает 3. Следовательно, остаток от деления 27 на 4 составляет 3:
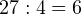
Пример 2. Деление с остатком отрицательного целого числа на положительное целое число.
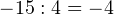
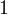
Пример 3. Деление положительного целого числа на отрицательное целое число.
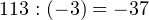
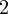
Пример 4. Деление с остатком отрицательного целого числа на отрицательное целое число.
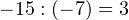
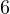
Проверьте, насколько хорошо вы поняли этот урок. Найдите самостоятельно остаток от деления отрицательных чисел:
Свои ответы пишите в комментариях, я их проверю.