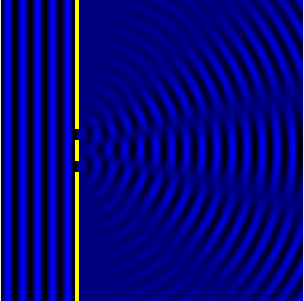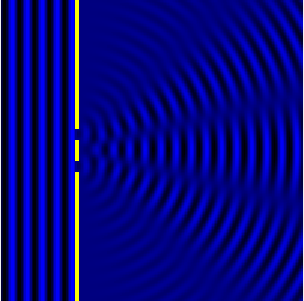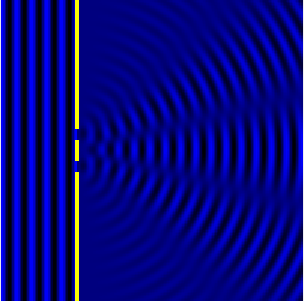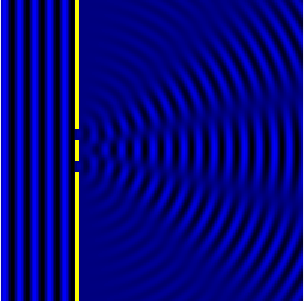
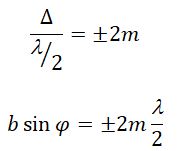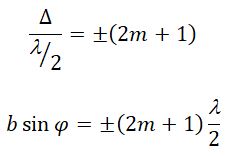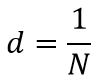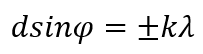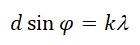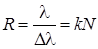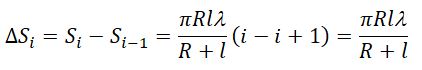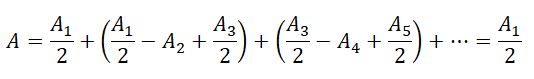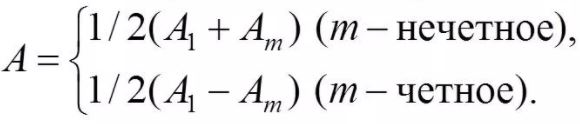если препятствие велико по сравнению с длиной волны при каких условиях можно наблюдать дифракцию
Если препятствие велико по сравнению с длиной волны при каких условиях можно наблюдать дифракцию
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Свойства дифракции:
1) Дифракция волн – характерная особенность распространения волн независимо от их природы.
3) Дифракция волн зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. В пределе при λ→0 законы волновой оптики переходят в законы геометрической оптики. Дифракция обнаруживается в тех случаях, когда размеры огибаемых препятствий соизмеримы с длиной волны.
Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.
Дифракция Фраунгофера от одной щели
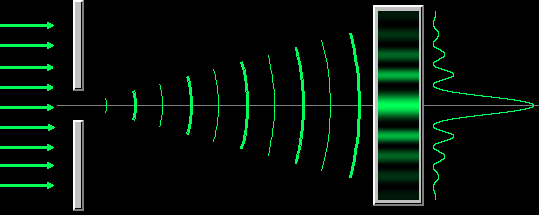
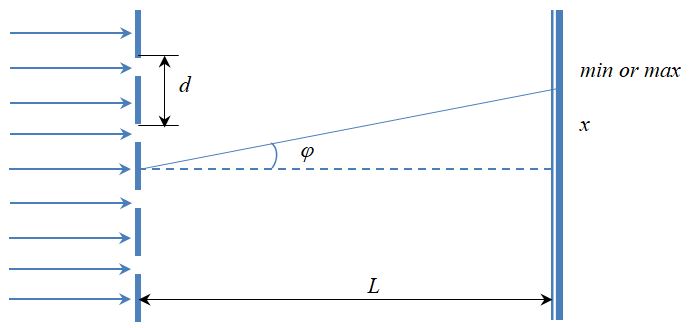
Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.
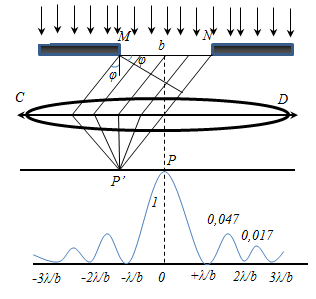
Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.
Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:
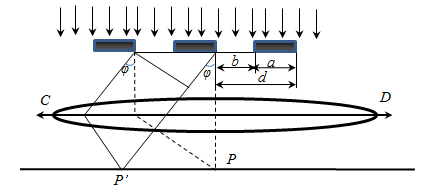
Дифракционная решетка
Совокупность большого числа щелей и промежутков между ними называется дифракционной решеткой.
В областях, в которых существует минимум при одной щели, минимумы будут и в случае N щелей, т. е. условие первичного минимума дифракционной решетки аналогично условию минимума для одной щели:
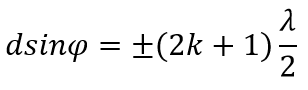
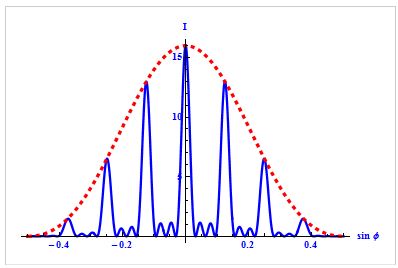
— условие главных минимумов.
Условие главных максимумов :
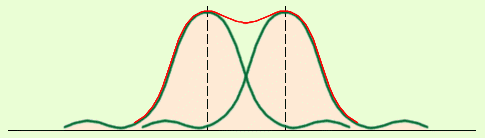
Эти максимумы расположены симметрично относительно центра (k = 0) и главного максимума.
Между главными максимумами будут расположены (N-1) дополнительных минимумов.
Разрешающая способность дифракционной решетки
Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Но в высокоточных астрономических приборах реализуется дифракционный предел качества изображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимыми от изображения одной точки.
Спектральной разрешающей способностью R решетки, характеризующей возможность разделения с ее помощью двух близких спектральных линий с длинами волн λ и λ + Δλ, называется отношение длины волны λ к минимально возможному значению Δλ
Действие оптических приборов описывается законами геометрической оптики. Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними. Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.
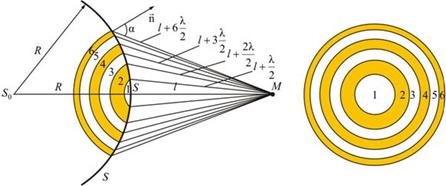
Метод зон Френеля
Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ = λ/2.
Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: A = A1 + A2 + A3 +. + Ai.
где A – амплитуда результирующего колебания, Ai – амплитуда колебаний, возбуждаемая i-й зоной Френеля.
Величина Ai зависит от площади Si зоны и угла αi между нормалью к поверхности и прямой, направленной в точку M.
Площадь одной зоны
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.
Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.
.
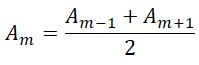
Тогда выражение для амплитуды можно записать в виде
Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда А = A1 /2.
Интенсивность излучения J
Так как радиус центральной зоны мал ( r1 = 0,16 мм), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.
Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна A1. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. J = 4J1 ). Интенсивность света увеличивается, если закрыть все четные зоны.
Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
Дифракция на простых объектах
Дифракция на щели
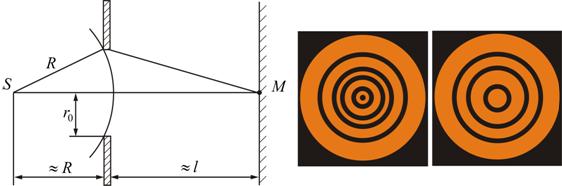
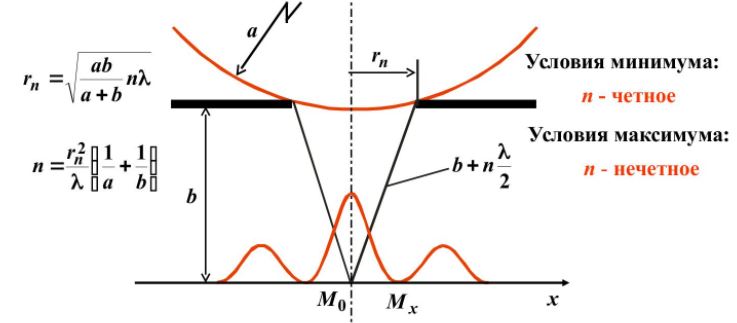
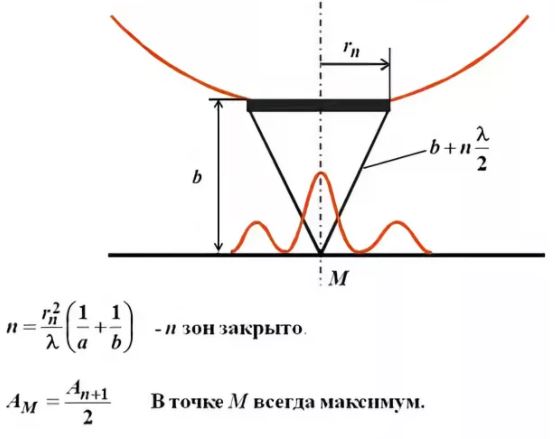
Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. К огда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю.
Дифракция на круглом отверстии при открытом чётном (слева) и не чётном (справа) числе зон.
Естественно, что если r0>>λ, то никакой дифракционной картины не будет.
Дифракция от диска
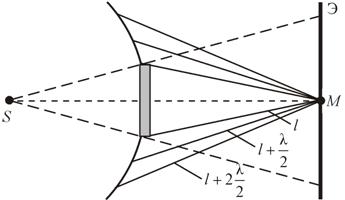
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.
В центре тени светлое пятно
Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).
Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.
Если препятствие велико по сравнению с длиной волны при каких условиях можно наблюдать дифракцию
Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.
Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
ДИФРАКЦИЯ СВЕТА
Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.
Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.
Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).
Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.
Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.
Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.
Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.
На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.
Зоны Френеля для трехсантиметровой волны
Зонная пластинка для трехсантиметровых волн
Дифракция волн.
Дифракция волн (от лат. diffractus — разломанный) — в первоначальном узком смысле — огибание волнами препятствий, в современном — более широком — любые отклонения при распространении волн от законов геометрической оптики.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
Способность волн огибать препятствия можно наблюдать на морских волнах, легко огибающих камень, размеры которого малы по сравнению с длиной волны. Звуковые волны также способны огибать препятствия, благодаря чему мы слышим, например, сигнал машины, находящейся за углом дома.
Явление дифракции волн на поверхности воды можно наблюдать, если поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны.
За экраном распространяется круговая волна, как если бы в отверстии экрана располагалось колеблющееся тело — источник волн. Согласно принципу Гюйгенса-Френеля, так и должно быть. Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.
Если размеры щели велики по сравнению с длиной волны, то волна проходит сквозь щель, почти не меняя своей формы, лишь по краям видны еле заметные искривления волновой поверхности, благодаря которым волна проникает и в пространство за экраном.
Дифракция (волн, света)
Дифракция это отклонение волны или света от прямолинейного распространения, к примеру некоторое огибание волн препятствий на поверхности воды, дифракция света почти не существует но ее можно наблюдать с помощью некоторых приборов или равномерно запыленной пластинки. Дифракцию света можно также наблюдать в полнолуние когда на небе есть как бы туман или зимой в сильный мороз, образуется одинарный или больше кругов во круг луны.
Что такое дифракция волн
Это — любое отклонение волны от прямолинейного распространения. Весьма важным случаем дифракции является огибание волной краев препятствия, расположенного на пути распространения волны.
Рассмотрим дифракцию волн на поверхности воды. Если на пути волны находится достаточно широкое плоское препятствие, например экран Э, то позади него образуется свободное от колебаний пространство, называемое тенью. Края тени ограничены лучами, проведенными из источника у краев препятствия. Если постепенно уменьшать ширину экрана, то волна начинает огибать его края и заходит в область тени на некоторый угол а.
Чем уже будет препятствие, тем сильнее будет огибание его краев волной. Наконец, если ширина препятствия станет близкой к длине волны, то тень исчезнет и волны, огибая препятствие, будут полностью замыкаться на небольшом расстоянии от него (заметим, что применительно к световой волне отсутствие тени означает невидимость тела).
Угол α, на который отклоняются от первоначального направления лучи дифрагировавшей волны называется углом дифракции. Угол дифракции а тем больше, чем меньше ширина препятствия или отверстия, через которое проходит волна, сравнительно с длиной волны. Следовательно, при данной ширине d препятствия или отверстия угол дифракции α тем больше, чем больше длина волны λ, или при данной длине волны λ угол дифракции а тем больше, чем меньше ширина d отверстия или препятствия.
Дифракция волн хорошо объясняется с точки зрения принципа Гюйгенса— Френеля. Возьмем пример дифракции волны при прохождении через узкую щель, перпендикулярную плоскости рисунка. Рассматривая точки поверх ности волны, построенной внутри щели, как центры образования вторичных круговых волн, можно построить новую поверхность волны как огибающую к ним.
Рассеяние волны
Если в среде, в которой распространяется волна, имеются мелкие инородные частицы или неоднородности в строении самой среды, то волна, дос тигая их, вызывает образование вокруг них элементарных круговых волн, распространяющихся во все стороны. Интенсивность основной волны при этом ослабляется. Это явление называется рассеянием волны и также относится к дифракции.
Образование рассеянных волн можно показать, если поместить в нашей ванне препятствие, меньшее по размерам длины волны, и затем вызвать ряд отдельных волн. Каждая из этих волн, достигая препятствия, будет вызывать образование вокруг него как центра новой круговой волны, хотя и весьма слабой по интенсивности.
Дифракция света
В практической жизни дифракция света почти не наблюдается. Это связано с тем, что большая часть окружающих тел имеет размеры, значительно превышающие длину волны света. В этом случае дифракцию можно наблюдать только при условии, что световая волна, претерпевшая дифракцию, отбрасывается на достаточно далеко (десятки метров) расположенный экран.
Эти кольца образуются в результате интерференции лучей, дифрагировавших при прохождении через запыленный слой пластинки. Подобные круги видны в морозный день вокруг солнца; роль пылинок здесь выполняют находящиеся в воздухе мельчайшие кристаллы льда. Цветные круги вокруг светящихся предметов появляются при заболеваниях глаз, связанных с помутнением прозрачных сред самого глаза, и т. д.
Дифракционное изображение
Образование дифракционного изображения щели можно объяснить на основании принципа Гюйгенса — Френеля. Отдельные точки поверхности волны, проходящей через щель, могут рассматриваться как центры вторичных круговых волн (рис. 2). Эти волны, распространяясь за пределами щели, интерферируют между собой, и картина, получающаяся на экране Э, зависит от разности хода, образующейся между ними для различных точек экрана.
Дифракционное изображение малого отверстия, освещенного параллельным пучком монохроматических лучей, представляет светлое пятно, окруженное чередующимися темными и светлыми кольцами; при освещении белым светом получается белое пятно, окаймленное цветными кольцами. Наличие интерференционных колец в изображении малого отверстия затрудняет суждение о его форме и величине, а при наличии нескольких близко расположенных отверстий может препятствовать их различению или, как называют в оптике, их разрешению.
Дифракционная решетка
Дифракционный спектроскоп. При изучении дифракционных явлений применяется дифракционная решетка. Она состоит из непрозрачной для света пластинки, в которой имеется большое число узких параллельных щелей. Решетка освещается от сильного источника пучком параллельных лучей (дифракция Фраунгофера). Результат дифракции наблюдается на экране, помещенном в фокальной плоскости собирающей линзы, расположенной впереди решетки. Линза фокусирует параллельные лучи, отклонившиеся в результате дифракции в отдельных щелях решетки.
Дифракционная решетка изготовляется из стеклянной пластинки, на которой алмазным острием наносится необходимое количество параллельных штрихов. Штрихи затираются черной краской. Неповрежденное стекло между штрихами служит щелями решетки . Расстояние d между центрами соседних щелей называется периодом или постоянной решетки.
Лучи, дифрагировавшие под различными углами, будут иметь различную разность хода. В зависимости от соотношения разности хода ∆ с длиной волны λ определится результат интерференции: усиление колебаний в точках, для которых разность хода равняется нулю или четному числу полуволн:
(рис. 3, в); 2λ, 3λ и т. д. или ослабление колебаний при разности хода, равной нечетному числу полуволн:
Досл = λ/2
(рис. 3, б); (3/2)λ; (5/2)λ и т. д. В результате дифракционная картина в фокальной плоскости линзы будет состоять из центральной светлой полосы и чередующихся темных и светлых боковых полос, постепенно убывающих по яркости.
Относительная яркость дифракционных максимумов показана в виде графика в правой части рисунка. С возрастанием порядкового номера яркость максимумов значительно убывает. Ширина дифракционных максимумов, а также расстояние между ними зависят от периода решетки: чем меньше период, тем шире полосы и тем дальше расположены они от средней линии.
В соответствии с порядком того или иного максимума, обозначаемого буквой m, будет различаться как разность хода ∆, так и угол отклонения α лучей, образующих этот максимум.
Например: для максимума 1-го порядка (m =1): ∆1 = d sin α1= λ; для максимума 2-го порядка (m = 2):
и т. д.; для максимума т порядка:
Рассмотрим дифракцию плоской монохроматической волны, падающей перпендикулярно на две узкие параллельные щели (рис. 3). Предположим, что в каждой щели образуется по одной вторичной волне. Эти волны когерентны и за щелями будут интерферировать между собой. Результат интерференции двух параллельных лучей OA и О’А’ (рис. 3, а), которые отклонились в щелях под одинаковым углом а к первоначальному направлению и которые линзой собираются в одну точку фокальной плоскости, зависит от разности хода А, образовавшейся между ними в связи с изменением их направления (преломление лучей в линзе на разность хода не влияет). Если из точки О‘, в которой луч О’А’ изменяет направление, опустить перпендикуляр на луч OA, то О’В есть фронт дифрагировавшей волны, а отрезок ОВ есть разность хода между этими лучами:
Разность хода А можно выразить через расстояние d между центрами щелей и угол α отклонения лучей: из треугольника ОО’В, в котором угол при вершине О равен углу а, находим:
∆ = d sin α
Последнее соотношение называется формулой дифракционной решетки.
Если на решетку падает белый свет, то положение максимумов одного и того же порядка для лучей с различной длиной волны будет разным, в результате чего каждый максимум состоит из системы цветных полос, которая называется дифракционным спектром.
Максимумы нулевого порядка, совпадая для всех длин волн, дают центральную белую полосу О, максимумы первого порядка отделены от нее темными промежутками N и образуют отчетливые картины спектров первого порядка, фиолетовые полосы которых расположены ближе к центру, а красные — дальше от центра. Дальше располагаются спектры более высоких порядков, однако в них уже может происходить наложение цветных полос спектров различного порядка.
В связи с тем что расположение цветных полос в дифракционном спектре более равномерно, чем в спектре, который получается с помощью призмы, этот спектр называется нормальным спектром.
Дифракционный спектроскоп
С помощью дифракционной решетки может быть измерена длина волны светового излучения. Прибор называется дифракционным спектроскопом и устроен аналогично призменному спектроскопу, только вместо призмы в центре диска Д устанавливается дифракционная решетка. При измерении зрительная труба з устанавливается по направлению соответствующего максимума. Угол αт, измеренный при этом по шкале диска Д, равен углу, под которым отклоняются лучи, образующие этот максимум. Длина волны λ находится по формуле дифракционной решетки: λ = d sin αm, где d — период решетки.
Длины волн, соответствующие основным цветам спектра, приведены в таблице.
| Цвет | Длина волны в ммк |
| Красный | 760—620 |
| Оранжевый | 620—590 |
| Желтый | 590—575 |
| Желто-зеленый | 575—550 |
| Зеленый | 550—510 |
| Голубой | 510—480 |
| Фиолетовый | 450—380 |
Дифракция при наклонном падении лучей на решетку
Рассмотрим дифракцию пучка параллельных монохроматических лучей, падающих на решетку под углом φ : проходя через щели, лучи вследствие дифракции отклоняются от первоначального направления в обе стороны на некоторые углы γ’ и γ«. Эти углы определяют направления на соответствующие дифракционные максимумы. Обозначим α1‘ и α2» углы, образуемые этими лучами, с перпендикуляром к плоскости решетки, который является оптической осью системы.
Для наших рассуждений существенно то, что при одной и той же степени дифракции угол α’ отклонения от оптической оси системы для лучей OA’ при любом угле падения φ будет меньше, а угол α» для лучей OA» больше, чем соответствующие углы при перпендикулярном падении лучей на решетку.
Поскольку лучи OA’ с меньшим отклонением от оптической оси системы будут использованы в дальнейшем изложении, определим для них разность хода при образовании максимумов того или иного порядка. При этом углы отклонения лучей будем отсчитывать от оптической оси системы. Для этого из точки изменения направления хода первого луча опустим перпендикуляры b а и bd на второй луч.
Отрезки ас и cd в сумме образуют расстояние, на которое путь второго луча больше, чем путь первого. Разность хода лучей ∆1‘ = ac + cd. Из треугольников abc и cbd отрезки ас и cd можно выразить через период d решетки и углы при вершинах этих треугольников, равные углам падения и отклонения дифрагированных лучей:
ас = d sin φ иcd = d sin α’1.
Максимум нулевого порядка будет располагаться по направлению падения лучей (разность хода ∆0 =0), максимум первого порядка — по угловому направлению, обусловленному соотношением
∆1‘ = d (sin α’1 + sin φ) = λ и т. д.
Лучи OA» представляют для нас меньший интерес. Заметим только, что, ориентируясь на систему этих лучей, можно получить большое откло нение лучей от оптической оси системы даже при малой степени дифракции, т. е. на грубых решетках с большим периодом, дифракция на которых при перпендикулярном падении лучей почти незаметна.
Рассеяние света
Одним из видов дифракции является рассеяние света на неоднородностях среды, через которую свет проходит. Прямой свет, падая на мельчайшие неоднородности среды, изменяет направление таким образом, что распространяется от них во все стороны, в связи с чем. они наблюдаются как слабо светящиеся точки (несамостоятельное свечение).
Рассеяние света может происходить, например, на частицах пыли или дыма в воздухе, на частицах тумана, на мелкодисперсной эмульсии жира в воде и т. д. Подобные среды называются мутными, а рассеяние света на них — эффектом Тиндаля.
Рассеяние света в мутной среде
Рассеяние света в мутной среде можно продемонстрировать следую щим опытом. В энергично перемешиваемую воду вливают несколько капель спиртового раствора канифоли; спирт смешивается с водой и канифоль выделяется в виде мельчайших, не различимых глазом твердых частичек. Если через такую среду пропустить узкий пучок света, то он будет виден сбоку в виде слабо светящейся полоски, прямые лучи при этом сильно ослабляются (рис. 4, а). Аналогичное явление можно наблюдать, когда узкий пучок лучей проходит сквозь запыленную атмосферу: свет рассеивается на пылинках и весь пучок становится видимым в любом направлении.
Рассеяние света на пространственных неоднородностях среды происходит тем интенсивнее, чем мельче эти неоднородности сравнительно с длиной волны света.
С точки зрения принципа Гюйгенса в основе рассеяния света лежит образование вторичных круговых волн, возбуждаемых первичной волной падающего света, вокруг центров, которыми являются мельчайшие неодн ородности среды. Эти волны и являются волнами рассеянного света.
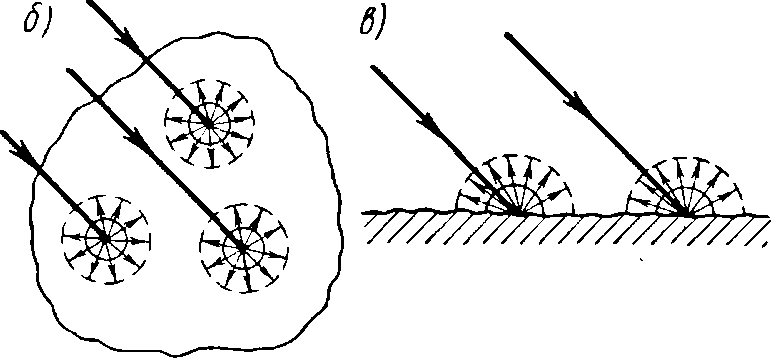
Если рассматривать ход лучей, то явление представляется таким образом: прямые лучи падают на мельчайшие неоднородности среды, от которых по всем направлениям (включая и направление, обратное падающему свету) расходятся лучи рассеянного света, значительно более слабые по интенсивности (рис. 4, б).
Рассеяние света в газе
Рассеяние света происходит также в среде чистого газа (например, атмосферного воздуха) около центров колебаний (флюктуации) плотности газа, происходящих в результате беспорядочного теплового движения молекул газа. Этот вид рассеивания называется молекулярным.
Интенсивность рассеяния зависит от длины волны света: короткие волны рассеиваются значительно сильней, чем длинные. Интенсивность Iрас рассеянного света в дисперсных средах с размерами неоднородностей, меньшими длины волны, обратно пропорциональна примерно четвертой степени длины волны (закон Рэлея).
Вследствие рассеяния в атмосфере преимущественно коротких волн цвет неба представляется нам сине-голубым, а прямое солнечное излучение приобретает желто-красный оттенок, особенно при восходе и заходе солнца, когда оно проходит более длинный путь в атмосфере.
Интенсивность света, рассеянного на относительно крупных частицах, обратно пропорциональна этой степени длины волны. Поэтому, например, мелкодисперсный туман имеет синий цвет, а состоящий из более крупных капелек — белый.
Рассеяние света происходит также на мельчайших неровностях (шероховатостях) поверхности раздела, различных по оптическим свойствам сред (рис. 4, в). Такие поверхности называются матовыми, а само явление — поверхностным рассеянием или диффузным отражением. Интенсивность рассеянного света в этом случае обратно пропорциональна второй степени длины волны. Коэффициент диффузного отражения от поверхностей называется альбедо.
Статья на тему Дифракция
Похожие страницы:
Понравилась статья поделись ей