если в общем уравнении плоскости какой либо коэффициент равен нулю то оно называется
Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
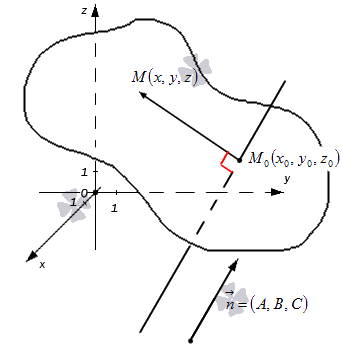
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Раскроем чуть шире смысл теорем.
Укажем пример как иллюстрацию этих утверждений.
Общее уравнение плоскости, проходящей через точку
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Решение
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Возможно получить это уравнение другим способом.
Решение
Рассмотрим два способа решения.
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
Неполное общее уравнение плоскости
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
Решение
Задачу возможно решить еще одним способом.
Решение
Уравнение плоскости, виды уравнения плоскости
В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.
Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
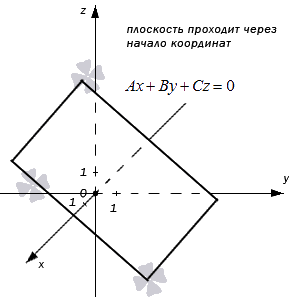
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Нормальное уравнение плоскости
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
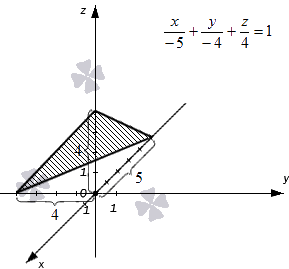
Уравнение плоскости в отрезках
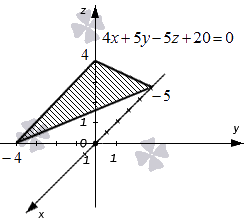
Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
Уравнение плоскости, виды уравнения плоскости.
В разделе плоскость в пространстве мы рассмотрели плоскость с позиций геометрии. В этой статье мы взглянем на плоскость с позиций алгебры, то есть, перейдем к описанию плоскости с помощью уравнения плоскости.
Сначала разберемся с вопросом: «Что такое уравнение плоскости»? После этого рассмотрим основные виды уравнения плоскости в прямоугольной системе координат Oxyz трехмерного плостранства.
Навигация по странице.
Уравнение плоскости – определение.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и задана плоскость.
Плоскость, как и любая другая геометрическая фигура, состоит из точек. В прямоугольной системе координат Oxyz каждой точке соответствует упорядоченная тройка чисел – координаты точки. Между координатами каждой точки плоскости можно установить зависимость с помощью уравнения, которое называют уравнением плоскости.
Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.
Осталось выяснить, какой вид имеет уравнение плоскости. Ответ на этот вопрос содержится в следующем пункте этой статьи. Забегая вперед, отметим, что уравнение плоскости может быть записано по-разному. Существование различных видов уравнения плоскости обусловлено спецификой решаемых задач.
Общее уравнение плоскости.
Приведем формулировку теоремы, которая дает нам вид уравнения плоскости.
Следует заметить, что уравнение вида 





Немного поясним смысл озвученной теоремы. В прямоугольной системе координат Oxyz каждой плоскости соответствует ее уравнение общего вида 

Неполными уравнениями задаются плоскости, параллельные координатным осям, проходящие через координатные оси, параллельные координатным плоскостям, перпендикулярные координатным плоскостям, совпадающие с координатными плоскостями, а также плоскости, проходящие через начало координат.
Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.
Рекомендуем ознакомиться с материалом статьи общее уравнение плоскости, где информация по теме изложена детальнее, подробно разобраны решения характерных примеров и задач.
Уравнение плоскости в отрезках.
Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках 

Для получения более полной информации обращайтесь к статье уравнение плоскости в отрезках, там показано приведение уравнения плоскости в отрезках к общему уравнению плоскости, там же Вы также найдете подробные решения характерных примеров и задач.
Нормальное уравнение плоскости.
Общее уравнение плоскости вида 



Часто можно видеть, что нормальное уравнение плоскости записывают в виде 


Приведем пример нормального уравнения плоскости.
Пусть плоскость задана в прямоугольной системе координат Oxyz общим уравнение плоскости вида 



Уравнение плоскости в нормальном виде позволяет находить расстояние от точки до плоскости.
Рекомендуем более детально разобраться с данным видом уравнения плоскости, посмотреть подробные решения характерных примеров и задач, а также научиться приводить общее уравнение плоскости к нормальному виду. Это Вы можете сделать, обратившись к статье нормальное уравнение плоскости.
Продолжим изучение темы уравнение плоскости. В этой статье мы всесторонне рассмотрим общее уравнение плоскости в трехмерном пространстве в фиксированной прямоугольной системе координат. Сначала получим вид общего уравнения плоскости, приведем примеры и необходимые пояснения. Далее остановимся на общем уравнении плоскости, проходящей через заданную точку пространстве. В заключении разберем частные случаи общего уравнения плоскости, рассмотрим общее неполное уравнение плоскости и приведем подробные решения задач.
Навигация по странице.
Прежде чем записать общее уравнение плоскости, напомним определение прямой перпендикулярной к плоскости: прямая перпендикулярна к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Из этого определения следует, что любой нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в этой плоскости. Этот факт мы используем при доказательстве следующей теоремы, которая задает вид общего уравнения плоскости.
Начнем с доказательства первой части теоремы.
Равенство 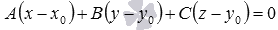

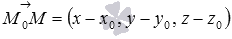
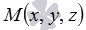
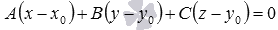

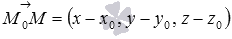
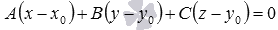

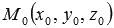
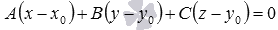

Приступим к доказательству второй части.
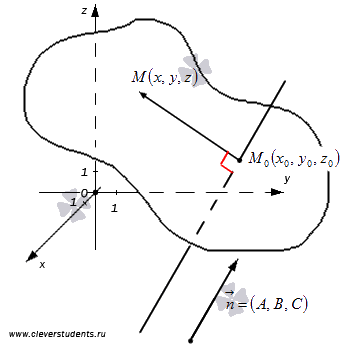
Пусть нам дана плоскость, проходящая через точку 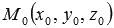


Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет 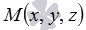

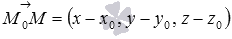
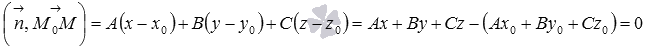
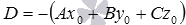

Уравнение 
Общее уравнение плоскости вида 




Немного поясним смысл теоремы.
Приведем пример, иллюстрирующий последнюю фразу.
Общее уравнение плоскости, проходящей через точку.
Еще раз повторим, что точка 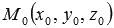

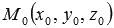

Принадлежат ли точки 


Подставим координаты точки М0 в общее уравнение плоскости: 

Проделаем такую же процедуру с координатами точки N0 : 


М0 лежит в плоскости, а N0 – не лежит.
Из доказательства теоремы об общем уравнении плоскости виден один полезный факт: вектор 

Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости 
Теперь рассмотрим обратную задачу – задачу составления уравнения плоскости, когда известны координаты ее нормального вектора. Очевидно, что существует бесконечно много параллельных плоскостей, нормальным вектором которых является вектор 
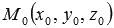

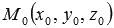
Общее уравнение плоскости с нормальным вектором 

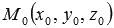
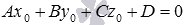

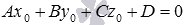
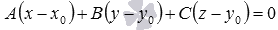
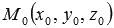

Это уравнение можно было получить и иначе.
Очевидно, что множество точек трехмерного пространства 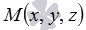

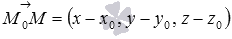

Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку 

Приведем два решения этой задачи.
Из условия имеем 
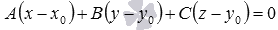
Теперь второй вариант решения.
Пусть 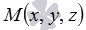




Существует множество аналогичных задач на составление общего уравнения плоскости, в которых сначала требуется найти координаты нормального вектора плоскости. Самые распространенные из них это задачи на нахождение уравнения плоскости, проходящей через точку параллельно заданной плоскости и задачи на составление уравнения плоскости, проходящей через точку перпендикулярно к заданной прямой.
Неполное общее уравнение плоскости.
Рассмотрим все возможные общие неполные уравнения плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.
Разберем решения нескольких примеров на составление неполного уравнения плоскости.
Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку 
Приведем второй способ решения этой задачи.