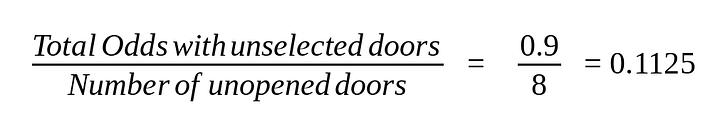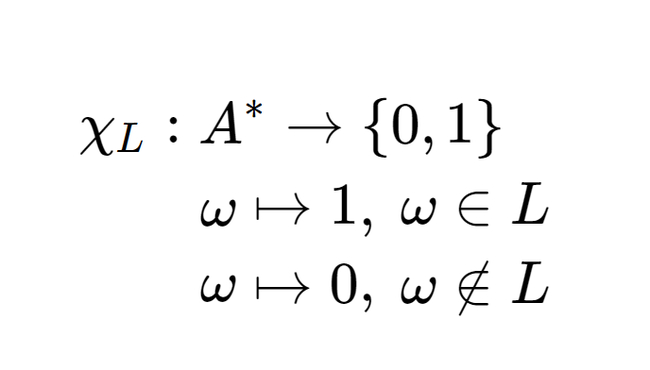есть 3 двери в какую ты зайдешь
Загадка про три двери. А ты знаешь ответ?!
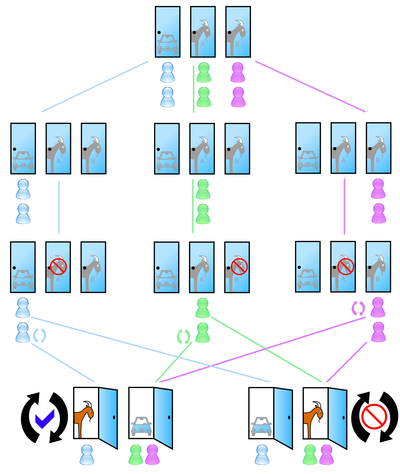
1. Вы играете в игру на телепередаче. Перед вами три двери, за одной из них приз. Вам надо выбрать. Вы прислушиваетесь к интуиции и показываете на правую дверь.
2. После выбора, ведущий не трогает вашу дверь, но открывает другую, которая находится в середине. Вы видите, что приза там нет. Приз находится либо в правой двери, которую вы выбрали, либо в левой двери, которая осталась.
3. Ведущий до сих пор не открывает вашу дверь. Теперь он предлагает изменить решение — показать на левую дверь вместо правой.
4. Вопрос — что вы будете делать? Измените решение и покажете на левую дверь? Решите, что ведущий вас запутывает, и оставите первоначальный выбор? Или скажете, что шансы 50 на 50, и решение не имеет значения?
5. Правильный ответ — нужно менять дверь. Так вы заберете приз с вероятностью 66%.
6. Для объяснения ситуации давайте рассмотрим две стратегии игры. В обеих стратегиях мы выбираем первую дверь случайным образом. Но в первой стратегии мы никогда не соглашаемся на предложение ведущего и твердо стоим на своем. Во второй стратегии наоборот — не задумываясь меняем решение.
7. Чтобы победить в первой стратегии, мы должны угадать нужную дверь на первом этапе игры. Тогда на втором этапе мы сохраним первоначальное решение и заберем приз, когда дверь откроется.
8. Чтобы победить во второй стратегии, на первом этапе игры мы должны ошибиться. Тогда мы автоматически попадем на призовую дверь, когда поменяем решение.
9. А теперь посчитаем вероятности. В стартовой точке перед нами три двери. Приз только за одной. Соответственно, вероятность указать на приз составляет ⅓, а вероятность ошибиться — ⅔. То есть, когда мы используем первую стратегию и оставляем решение, мы побеждаем один раз из трех. А когда используем вторую стратегию и меняем решение, то побеждаем два раза из трех.
10. Таким образом, сыграв в игру девять раз подряд по второй стратегии, мы шесть раз заберем приз. И три раза ошибемся.
Вывод №1. Нужно учитывать новую информацию. Если мы сделали выбор, а через минуту вышла важная новость, то есть смысл пересмотреть решение. За счет этого можно получить преимущество.
Вывод №2. Математика работает лучше интуиции. Если мы можем математически смоделировать ситуацию и оценить вероятности, то этим надо пользоваться.
Вывод №3. На сайте топикстартера есть полезный контент для инвесторов. В телеграм-канале топикстартера полезного контента еще больше. Поэтому ни на что не намекаю, но стоит подписаться, чтобы не пропустить новые материалы.
Тест: Какую дверь вы откроете? Первую, вторую или третью?
Тест-загадка на проверку внимательности и логического мышления
Тесты и логические загадки любит решать практически каждый из нас. Порою найденный ответ заставляет удивляться, иногда он оказывается настолько простым, что человек оказывается в недоумении.
В большинстве случаев ответ прячется на самом видном месте, но, чтобы его найти, нужно включить логическое мышление, построить в уме несколько ситуаций и прорабатывать их до решения теста.
К подобной категории относится тест про три двери, показывающий, насколько у человека развито образное мышление, внимательность, может ли он мыслить логически.
Условия теста
Итак, согласно условиям теста, перед вами имеется три двери. За каждой из них вас ждёт определённая опасность. За первой дверью – убийца, который так и ждёт, когда придёт его жертва. За второй дверью – свирепый лев, которого не кормили целый год. За третьей – полыхает пожар.
Вам обязательно нужно войти в одну из дверей. Подумайте немного, проанализируйте возможное развитие ситуаций, и выбирайте вашу дверь. После этого можно перейти к правильным ответам на тест.
Ответ
Вы выбрали первую дверь
И вы явно ошиблись! Хладнокровный убийца никого не пощадит.
Вы выбрали вторую дверь.
Значит, ваша логика работает так, как надо. Внимательно читающие условия теста люди, наверное, обратили внимание на то, что лев ничего не ел целый год. А без еды такое длительное время никто не выживет. Соответственно, можно без опаски сюда входить. Поздравляем! Вы остались живы!
Вы выбрали третью дверь
Простейшее объяснение парадокса Монти Холла
Парадокс Монти Холла — это одна из тех математических задач, над решением которой уже долгое время бьются многие умы, и даже всемирно известных математиков она приводит в затруднение. Хотя идея, лежащая в основе этого парадокса, предельно ясна и понятна. Задача эта, строго говоря, и не парадокс вовсе, но называется так из-за неочевидности и парадоксальности предлагаемых решений и объяснений, которые становятся поводом для самых жарких дискуссий в Интернете. Их накал уступает, пожалуй, лишь спорам из-за оптической иллюзии так называемого «платья раздора» и аудиоиллюзии «Янни и Лорел». Предлагаемое здесь объяснение призвано раз и навсегда развеять все связанные с этим парадоксом вопросы и очень доходчиво разъяснить всем интересующимся его суть.
Парадокс
Парадокс впервые был сформулирован американским математиком Стивом Селвином ещё в 1975 году, но широкую известность он приобрёл благодаря популярному игровому шоу «Давайте заключим сделку». В честь ведущего этой телевикторины, которого звали Монти Холл, парадокс и получил своё название.
В чём же суть парадокса Монти Холла?
Представьте, что перед вами три двери, как показано на рисунке ниже. За двумя дверьми находятся козы, за одной — автомобиль. Надо угадать дверь с автомобилем, и он ваш.
Казалось бы, ничего сложного. Но, как говорилось в одном фильме: «Если бы задача так просто решалась, то армянское радио этим бы не занималось». В своей передаче, после того как участник выбирал дверь, Монти всегда открывал одну из дверей с козой и предлагал ему поменять свой выбор. А вы поменяли бы или нет?
Этот вопрос многих ставит в тупик. Люди обычно думают: «Ну какая разница: остались две двери, и машина может с одинаковой вероятностью 50% оказаться как за одной, так и за другой дверью?». … И оказываются неправы. Правильный ответ — всегда менять первоначальный выбор. Поступая так, вы удваиваете свои шансы на победу.
Удивлены? Такой ответ для многих становится откровением: мало кто ожидает этого. Давайте подробно разберёмся, как так получается.
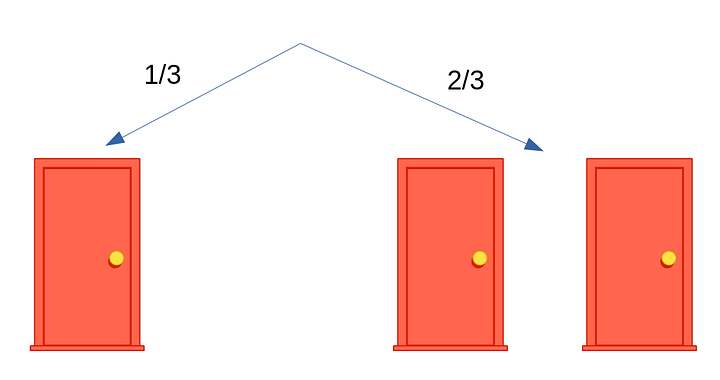
Итак, вы выбрали одну из трёх дверей. Вероятность того, что машина окажется именно за ней, составляет 1/3. А вероятность того, что она окажется за одной из двух оставшихся (то есть не выбранных вами) дверей, будет 2/3. Это должно быть понятно.
На рисунке у нас наглядно показаны эти вероятности: 1/3 слева и 2/3 справа.
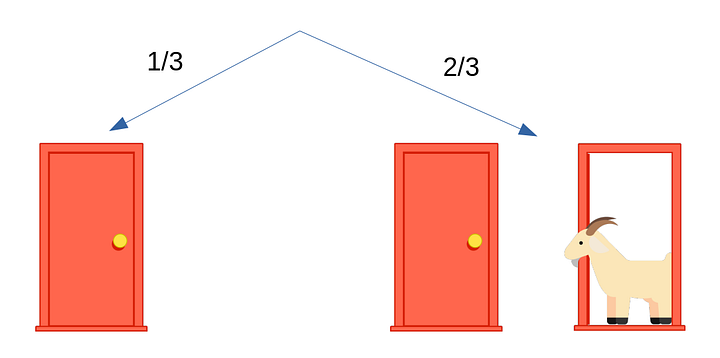
Теперь Монти открывает одну из невыбранных дверей — тех, что справа. И открывает он всегда ту, за которой коза.
Вероятности остаются неизменными: 1/3 слева (ваш первоначальный выбор) и 2/3 справа. Изменилось лишь то, что справа одна дверь теперь открыта, но вероятность для оставшейся неоткрытой двери здесь та же, что была прежде для обеих.
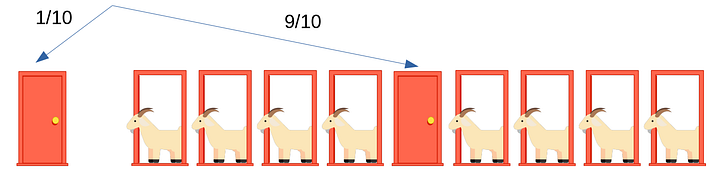
Если не совсем понятно, попробуем объяснить на примере с десятью дверьми.
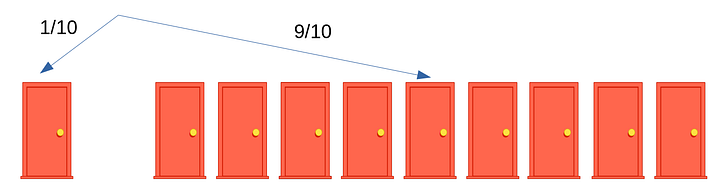
Выбранная вами дверь будет слева, остальные девять — справа (как на рисунке ниже). Вероятность того, что вы угадали дверь с машиной, будет 1/10. Вероятность того, что вы не угадали и машина окажется за одной из оставшихся девяти дверей, будет 9/10.
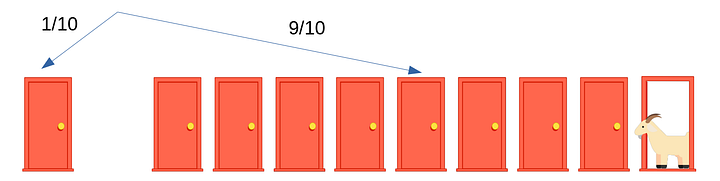
Дальше Монти открывает восемь из этих невыбранных девяти дверей, причем за всеми восемью — козы. Как поступить теперь: поменять свой выбор или нет? Конечно, поменять! Ведь теперь восемь из девяти дверей справа открыты, а вероятность того, что машина окажется за оставшейся девятой дверью (как мы уже посчитали ранее), равна 9/10.
Ответ на вопрос станет ещё очевиднее, если представить, что Монти даёт вам возможность открыть не одну оставшуюся справа неоткрытой дверь, а сразу все девять!
Вот и всё. Это так просто! Однако важно не забывать, что всегда есть вероятность проигрыша. Верное решение определяется стратегией. Правильная стратегия — делать так, чтобы шансы на победу были максимальными или хотя бы такими, которые позволяют больше выигрывать, чем проигрывать.
Усложняем задачу
Предположим, Монти хочет усложнить для вас задачу и открывает лишь одну дверь с правой стороны. Как вы поступите теперь: выберите одну из восьми закрытых дверей справа или не станете менять свой выбор?
Здесь придётся кое-что посчитать. Вероятность того, что машина окажется за одной из девяти дверей справа, равна 9/10. Разделим её на количество оставшихся неоткрытыми дверей (8):
Это будет вероятность того, что машина окажется за одной из восьми остающихся закрытыми дверей справа. И она чуть больше вероятности 0,1 (1/10), что первоначально выбранная вами дверь слева окажется с машиной. Поэтому вам всё же предпочтительнее поменять свой выбор, хотя шансы выиграть машину и в этом случае будут очень низкими. По этой же формуле можно посчитать вероятность для любого количества неоткрытых дверей.
Вот и весь парадокс Монти Холла вкратце. Не знаю, можно ли придумать более простое его объяснение? Я лишь выношу на ваш суд свой взгляд, отличный от тех, что изложены в большинстве других объяснений, в которых вы можете тоже почерпнуть много полезного. Надеюсь, что после прочтения статьи вы приблизились к пониманию парадокса Монти Холла.
Задача трёх дверей или парадокс Монти-Холла: интуитивно понятное объяснение
Оглавление: условия, объяснение, разбор популярных ошибок
Достаточно известна задача трёх дверей (парадокс Монти-Холла), о том, менять выбор или нет после убирание одного из вариантов. Напомню условия (из вики):
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Классическое объяснение подразумевает перебор вариантов. Но хоть это решение правильно с точки зрения математики, но совершенно не подходит для понимания.
Также замечу, что я вообще отказался от нумерации дверей, чтобы не привязываться к номерам. Также почти не опираюсь на то, что дверей три, чтобы можно было использовать доказательство для любого количество дверей. ключевые понят
Чтобы понять в чём соль парадокса, требуется взглянуть на шоу с другой точки зрения.
Есть первый игрок, есть ведущий (который знает правильную дверь). Переименуем ведущего во второго игрока, который тоже хочет открыть дверь с машиной (что верно, ибо открыв машину, первый игрок проиграет и выиграет ведущий). И второй игрок (ведущий) выбирает дверь вторым (выбирает дверь, которую оставить закрытой), после первого игрока и очевидно не может выбрать дверь первого игрока. После хода обоих игроков открывают все невыбранные двери и предлагают первому игроку поменять выбор на дверь второго игрока.
Условия полностью идентичны, первый игрок выбрал дверь, ведущий (мысленно) выбрал какую дверь он оставит (и потом предложит поменять на неё игроку), ведущий открыл все остальные двери, ведущий предложил игроку поменяться дверьми.
А теперь по шагам и с расчётом вероятности:
Первый игрок выбирает случайную дверь (успех с шансом 1/3).
Открывают все остальные невыбранные двери (в данном случае одну), которые очевидно пусты (машину либо угадал первый игрок, либо точно выбрал второй).
Итого, осталось две двери, одну которую выбрал первый игрок (случайно, 1/3) и вторую, которую выбрал второй игрок (ведущий, который знает где машина, 2/3). Вопрос, кто угадал вероятнее? Игрок, выбравший случайно или игрок-читер (ведущий), который только не мог выбрать дверь первого игрока?
Если понимать, что дверь, которую ведущий оставляет и на которую игроку предлагают сменить выбор не случайная, а специально задуманная ведущим, то парадокс становиться логичным и понятным.
Дверей осталось две, так что шанс 50%.
Более формальная запись: так как дверей осталось две, машина либо за одной, либо за другой, следовательно вероятности 50/50.
Для понимания ошибки вспомним анекдот: Какова вероятность выйти из дома и встретить динозавра? 50/50, либо да, либо нет.
Логика из анекдота: вариантов ответа только 2, да или нет. Следовательно вероятность 50/50.
Ошибка состоит в том, что из того факта, что дверей две, не следует что вероятности одинаковы. Следует, что суммарная вероятность найти за ними машину 100%. Две двери имели бы вероятность 50/50 если бы были случайны (что не так).
Две двери, которые остаются, случайные, так что шанс 50/50 (Усложнение предыдущей ошибки)
Если две оставшиеся двери случайны, значит, что двери одинаковы. То есть на то, какие двери остались нет никаких условий (или условия одинаковы). Дверь, выбранная первым игроком, очевидно, случайна и никаких условий не имеет. Соответственно, дверь, которая осталась (которую оставил ведущий), тоже не имеет никаких ограничений. То есть выбрана случайно. То есть ведущий выбрал дверь которую оставить случайно и открыл оставшуюся (которая тоже получается случайно). То есть из рассуждений получается, все двери (которую выбрал игрок, которую открыл ведущи, которую ведущий оставил) случайные. То есть дверь, которую открыл ведущий, случайная. А значит там может оказаться машина (вероятность 1/3). Но по условиям задачи это не так, так как она ТОЧНО без машины.
Ещё раз, две двери, которые оставляют, не случайны, так как дверь, которую оставляет ведущий, не случайная, так как дверь, которую открывает ведущий, не случайная. А не случайная, так как она точно пуста (если бы она была случайная, она бы могла случайно оказаться с машиной).
у игрока три варианта. шанс угадать 1/3
в одном случае он угадал, в двух случаях нет.
если он не угадал, и ведущий убрал лишний вариант, то чтобы выиграть, нужно поменять свой выбор.
если игрок не меняет выбор, его шансы выиграть
1/3*100% +2/3*0% =33%
если игрок меняет решение, то его шансы выиграть.
1/3*0% +2/3*100%=66%
Господа @Luros @Lude и мастер художественно запутать оппонента @targen
Официально заявляю, что я был не прав. Провел эксперимент на монетках разного достоинства, и выяснил, в чем именно я ошибался.
Не меняя выбор (т.е. сделав окончательный выбор в начале игры) игрок получает шанс выигрыша 1/3, не зависимо ни от чего, т.к. выбирал 1 вариант из 3 доступных.
Количество комментариев под этим постом было бы раз в 5 меньше, если кто-нибудь сразу предложил бы провести простой эксперимент. Или использовали бы в обсуждении аргумент, приведенный выше, а также аргументы “математически это не надо высчитывать, просто проверь”, “ты хуй” и “спорим на косарь”.
Благодарю за полемику, с вами было интересно спорить
Самое интуитивно понятное объяснение (для клинических случаев) это спор на деньги
Давайте уйдём от теории вероятности и придём к теории мошенничества. Ведущий знает за какой дверью выигрыш и знает, что игрок выбрал правильную дверь. Теперь ведущий, пользуясь аргументацией о теории вероятности, спровоцирует игрока на выбор неверной двери или не спровоцирует если игрок выбрал заведомо проигрышную дверь.
Есть 100 дверей. Одну вы выбрали, а потом ведущий открыл 98 дверей. Тут уже интуитивно понятно, что надо выбирать оставшуюся 99-ю.
@T0xaVolk, Представим, что ты, как игрок, изначально не угадал машину.
Теперь вопрос. В ситуации, когда игрок изначально не угадал машину, какова вероятность, что машина за другой дверью, на которую тебе предлагают сменить свой выбор?
“Я хочу отказаться от нумерации дверей, поэтому назову ведущего игрок номер два. “
Следите за руками за дверями. Ничего себе попроще объяснил. “В реальности всё не так, как на самом деле!”
А можно проще объяснить? Например: ведущий зная что выбранная вами дверь выигрышная, специально пытается вас сбить с толку, и именно поэтому выбранный вариант лучше оставить без изменений. Точка.
Да один черт, перед тобой три двери, за одной машина, хрен знает за какой, шансов 1\3, выбирай любую. То, что ведущий гарантированно забирает дверь с козой ничего не меняет, выбранная тобой первая дверь не становится от этого ни лучше, ни хуже.
Мужчина объясняет блогерше с тиктоком головного мозга на её вопросы
Успех гарантирован
У всего есть обратная сторона
Расслабьте яйца
Я вааще не ябу
чё хатят на бикабу
На нас обкатают, на всю страну распространят?
По новому Генплану жители, те, что ближе к побережью, обнаружили, что из дома попали в другие функциональные зоны. Было ИЖС, например, стало зона отдыха. Это значит, что люди не могут ничего построить на своей земле. Да даже дом отштукатурить нельзя! Генплан ещё не вступил в силу, а некоторые уже не могут прописаться в построенных домах.
У нас тут сейчас бурление, так сказать. Хотя, многие ещё не знают, многие ещё не верят.
Но некоторые думают, что так реализуется тот самый закон о всероссийской реновации. Когда за красивым названием стоит уничтожение прав собственности простых граждан.
Кидайтесь тапками, спорьте, ругайтесь, не верьте. Но все таки проверьте свою землю по кадастровому номеру в Росреестре. Говорят, что не только в Краснодарском крае эти ограничения 56.1 наложены
Парадокс Монти Холла (объяснение)
Я думаю, большая часть из вас, дорогие пикабушники, слышала об этом парадоксе, который по сути-то и не является настоящим парадоксом. Он назван так только потому, что простая человеческая интуиция никак не может принять обоснованный логический ответ и упорно сопротивляется. В этом посте я хотел бы рассказать об этом парадоксе тем, кто о нем не слышал, и постараться объяснить на пальцах, почему решение именно такое.
Ну что ж, начнем с самой формулировки:
“Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?”
Сначала попробуйте подумать сами над этой задачей и прийти к ответу.
Многие отвечают, что если изменить выбор двери, то ничего изменится, т.к. дверей осталось всего две, то есть вероятность выигрыша 50 на 50. Но это неверный ответ. Правильный ответ таков, что при смене двери шансы выиграть автомобиль увеличиваются аж в 2 РАЗА! Однако, казалось бы, почему если в конце произвольный выбор из двух дверей, то вероятность должна быть не 50 на 50? А все потому, что от начального выбора двери (когда их 3 закрытых),и будет зависеть то, какая дверь будет выбрана в конце.
Давай-те же теперь подробно разберемся, почему так происходит.
1)Предположим, что в начале игрок выбрал дверь с автомобилем (вероятность этого 1/3)
а)Игрок не меняет дверь, он выиграл АВТОМОБИЛЬ! (+)
б)Игрок меняет дверь и уходит домой с одной козой :(( (-)
2)Предположим, что в начале игрок выбрал дверь с козой (вероятность этого 2/3)
а)Игрок не меняет дверь и, опечалившись, уходит домой с козой (-)
б)Игрок меняет дверь и радостный уезжает на АВТОМОБИЛЕ домой (+)
Посмотрев на все возможные варианты развития событий, можно заметить, что при смене двери игрок уходит с козой, только если изначально была выбрана верная дверь, вероятность чего 1/3, а в ином случае с вероятность 2/3, он забирает ключи и валит из этого заведения на новенькой (или не очень) машине.
Ну вот и все, надеюсь Вам было интересно и понятно, что я написал. Также надеюсь, что Вам стал понятен ответ в этой вызывающей споры и большие дискуссии задаче 🙂
Всем пока и удачного дня)
P.s. Мой первый пост, однако судите, как хотите. Мне не нужны все эти “судите не строго”, мне нужна конструктивная критика.
Вероятность попадания 1-1/3=2/3. И никаких парадоксов.
У меня делема по поводу тех трех дверей. Действительно вероятность успеха при смене двери повышается в 2 раза, но зато вероятность неудачи при условии того что дверь не меняется падает в 2 раза.
Ну если на выбор 10 дверей. За одной дверью приз, за остальными нет. Вы указываете на одну дверь. Ведущий открывает оставшиеся 8 неверных дверей, кроме одной.
То это сразу понятно. А с тремя дверьми надо считать уже.
разрушители мифов по этому поводу наглядный эксперимент проводили. Очень убедительный
Не поверю, пока сам не проверю!
хоть и баян но я все равноне догоняяяюююююююююююююю
Так менять или нет. Объясни!
9l c4uTalO 4To Hy>l
Я понял =) попробую объяснить тем кто ещё не вшаривает.
Ведущий, точно зная где машина выбрал ту ячейку в которой осел и не выбрал ту которую выбрал игрок.
Проще говоря выбор во второй раз предлагают только тому кто заведомо выбрал неверный вариант!
В фильме “21” хорошо рассказано
Если вам предложат много раз выбирать и менять решение после того как открыли одну дверь, то все верно. Статистически доказано, что в большинстве раз вы будете в выигрыше. Но что будет, если вам предложат выбирать, и менять или не менять решение лишь один раз?
Вы ведь по-прежнему не знаете, за какой дверью автомобиль. Вам придется выбирать из двух дверей, а это50/50.
Вероятность
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
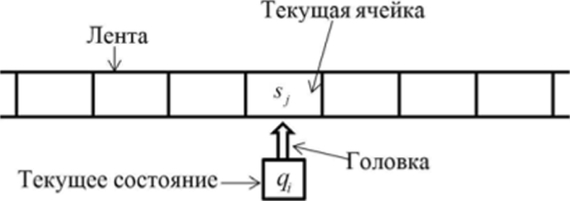
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
– выводит 1, только если w входит в язык L;
– для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
– функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
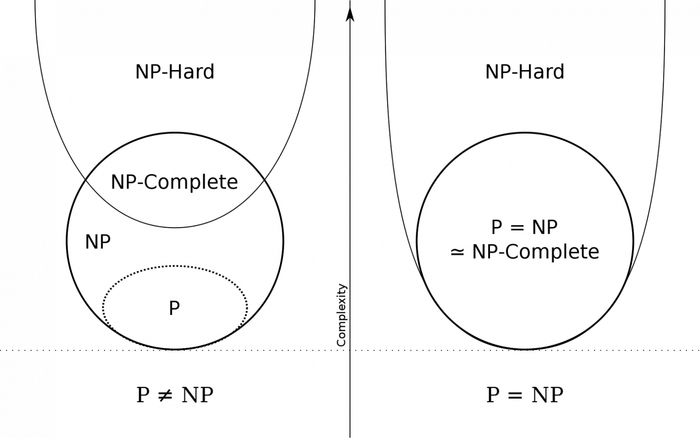
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.