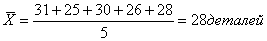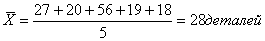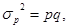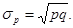коэффициент осцилляции показывает что
Коэффициент осцилляции показывает что
5.2 рПЛБЪБФЕМЙ ЧБТЙБГЙЙ
рПЛБЪБФЕМЙ ЧБТЙБГЙЙ ДЕМСФУС ОБ ДЧЕ ЗТХРРЩ : БВУПМАФОЩЕ Й ПФОПУЙФЕМШОЩЕ. тБУУНПФТЙН БВУПМАФОЩЕ РПЛБЪБФЕМЙ.
уБНЩН РТПУФЩН РПЛБЪБФЕМЕН СЧМСЕФУС ТБЪНБИ ЧБТЙБГЙЙ
 , , | (5.1) |
ЛПФПТЩК РПЛБЪЩЧБЕФ ОБУЛПМШЛП ЧЕМЙЛП ТБЪМЙЮЙЕ НЕЦДХ НЙОЙНБМШОЩН Й НБЛУЙНБМШОЩН ЪОБЮЕОЙЕН РТЙЪОБЛБ.
рПНЙНП РПЛБЪБФЕМС ТБЪНБИБ ЧБТЙБГЙЙ ДМС БОБМЙЪБ РТЙНЕОСЕФУС РПЛБЪБФЕМШ УТЕДОЕЗП МЙОЕКОПЗП ПФЛМПОЕОЙС, ЛПФПТЩК ПФТБЦБЕФ ЧУЕ ЛПМЕВБОЙС ЧБТШЙТХАЭЕЗП РТЙЪОБЛБ ПФ ПВПВЭБАЭЕК ЧЕМЙЮЙОЩ (УТЕДОЕК),ЧПЛТХЗ ЛПФПТПК РТПЙУИПДСФ ЛПМЕВБОЙС, ТБУУЕЙЧБОЙЕ ЪОБЮЕОЙК РТЙЪОБЛБ.
ьФПФ РПЛБЪБФЕМШ ПРТЕДЕМСЕФУС ЛБЛ УТЕДОЕЕ БТЙЖНЕФЙЮЕУЛПЕ ПФ УТЕДОЕК ЧЕМЙЮЙОЩ ( x ) РП УМЕДХАЭЙН ЖПТНХМБН:
 , , | (5.2) |
 . . | (5.3) |
ьФЙ ЖПТНХМЩ ДБАФ ПВЭХА ИБТБЛФЕТЙУФЙЛХ УФЕРЕОЙ ЛПМЕВМЕНПУФЙ РТЙЪОБЛБ Ч УПЧПЛХРОПУФЙ. пДОБЛП ЬФПФ РПЛБЪБФЕМШ ХУМПЦОСЕФ ТБУЮЕФЩ, ФБЛ ЛБЛ ДБЕФ ФПМШЛП РПМПЦЙФЕМШОЩЕ ПФЛМПОЕОЙС.
ч УФБФЙУФЙЮЕУЛЙИ ЙУУМЕДПЧБОЙСИ ЧБТЙБГЙЙ РТЙЪОБЛБ РТЙНЕОСАФ РПЛБЪБФЕМЙ ДЙУРЕТУЙЙ (УТЕДОЙК ЛЧБДТБФ ПФЛМПОЕОЙК).
пОБ РТЕДУФБЧМСЕФ УПВПК УТЕДОЙК ЛЧБДТБФ ПФЛМПОЕОЙК ЪОБЮЕОЙК ЙОДЙЧЙДХБМШОЩИ ЪОБЮЕОЙК РТЙЪОБЛБ ПФ ЙИ УТЕДОЙК ЧЕМЙЮЕОЩ. чЩЮЙУМСЕФУС РП ЖПТНХМБН :
 , , | (5.4) |
 . . | (5.5) |
дЙУРЕТУЙС ПВМБДБЕФ ТСДПН УЧПКУФЧ.
рТЙ ЙЪХЮЕОЙЙ ЧБТЙБГЙЙ ФБЛЦЕ РТЙНЕОСЕФУС УТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ. ьФПФ РПЛБЪБФЕМШ ТБУУЮЙФЩЧБЕФУС ЙЪЧМЕЮЕОЙЕН ЛПТОС ЛЧБДТБФОПЗП ЙЪ ДЙУРЕТУЙЙ РП ЖПТНХМБН:
 , , | (5.6) |
 . . | (5.7) |
уТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ ЙЗТБЕФ ЧБЦОХА ТПМШ Ч БОБМЙЪЕ ТСДПЧ ТБУРТЕДЕМЕОЙС. ч ХУМПЧЙСИ ОПТНБМШОПЗП ТБУРТЕДЕМЕОЙС УХЭЕУФЧХЕФ УМЕДХАЭБС ЪБЧЙУЙНПУФШ НЕЦДХ ЧЕМЙЮЙОПК УТЕДОЕЗП ЛЧБДТБФЮЕУЛПЗП ПФЛМПОЕОЙС Й ЛПМЙЮЕУФЧПН ОБВМАДЕОЙК:
– Ч РТЕДЕМБИ 
– Ч РТЕДЕМБИ 
– Ч РТЕДЕМБИ 
пФЛМПОЕОЙЕ 3 №115; НПЦЕФ УЮЙФБФШУС НБЛУЙНБМШОП ЧПЪНПЦОЩН. ьФП РПМПЦЕОЙЕ ОБЪЩЧБЕФУС “РТБЧЙМПН ФТЕИ УЙЗН”.
пФОПУЙФЕМШОЩНЙ РПЛБЪБФЕМСНЙ ЧБТЙБГЙЙ СЧМСАФУС:
1. лПЬЖЖЙГЙЕОФ ПУГЙММСГЙЙ
 | (5.8) |
2. мЙОЕКОЩК ЛПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ
 ЙМЙ ЙМЙ  | (5.9) |
3. лПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ
 | (5.10) |
юБЭЕ ЧУЕЗП ПОЙ ЧЩТБЦБАФУС Ч РТПГЕОФБИ Й ПРТЕДЕМСАФ ОЕ ФПМШЛП УТБЧОЙФЕМШОХА ПГЕОЛХ ЧБТЙБГЙЙ, ОП Й ДБАФ ИБТБЛФЕТЙУФЙЛХ ПДОПТПДОПУФЙ УПЧПЛХРОПУФЙ. уПЧПЛХРОПУФШ УЮЙФБЕФУС ПДОПТПДОПК, ЕУМЙ ЛПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ ОЕ РТЕЧЩЫБЕФ 33 % ( ДМС ТБУРТЕДЕМЕОЙС ВМЙЪЛЙИ Л ОПТНБМШОПНХ ).
йНЕАФУС ДБООЩЕ РП ЗТХРРЕ ТБВПЮЙИ:
| юЙУМЕООПУФШ ТБВПЮЙИ,ЮЕМ. | 2 | 4 | 8 | 9 | 7 | 5 | йФПЗП |
| 35 | |||||||
| чПЪТБУФ ТБВПЮЕЗП, МЕФ | 17 | 25 | 19 | 38 | 56 | 47 | – |
рП РПЛБЪБФЕМА ЧПЪТБУФБ ТБВПЮЙИ ПРТЕДЕМЙФШ: ТБЪНБИ ЧБТЙБГЙЙ, УТЕДОЕЕ МЙОЕКОПЕ ПФЛМПОЕОЙЕ, ДЙУРЕТУЙА, УТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ, ЛПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ.
1) тБЪНБИ ЧБТЙБГЙЙ ПРТЕДЕМСЕН РП ЖПТНХМЕ 5.1
2) уТЕДОЕЕ МЙОЕКОПЕ ПФЛМПОЕОЙЕ ПРТЕДЕМСЕН РП ЖПТНХМЕ 5.3. оБИПДЙН УТЕДОЙК ЧПЪТБУФ ТБВПЮЕЗП РП ЖПТНХМЕ 4.10
пРТЕДЕМСЕН
3) дЙУРЕТУЙС ПРТЕДЕМСЕФУС РП ЖПТНХМЕ 5.5
4) уТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ ПРТЕДЕМСЕН РП ЖПТНХМЕ 5.7
5) лПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ ПРТЕДЕМСЕН РП ЖПТНХМЕ 5.10
Коэффициент осцилляции показывает что
– область применения и методику расчёта степенных средних величин;
– исчислять степенные средние величины;
– формулировать вывод по полученным результатам.
Наряду со средними величинами в статистике исчисляются показатели вариации. Вариацией в статистике называются различия индивидуальных значений изучаемого признака. Возникает вариация в силу того, что отдельные значения признака статистической совокупности формируются под воздействием разнообразных факторов. Значение изучения вариации в том, что по колеблемости признаков можно судить о качественной однородности совокупности. Совокупности могут иметь одинаковые значения средней величины, но отличаться колеблемостью индивидуальных значений.
Например : По имеющимся данным о дневной выработке рабочих двух бригад определить среднюю выработку рабочего за день в каждой бригаде, сделать вывод об однородности рассматриваемых совокупностей и надёжности их средних.
Выработка в первой бригаде: 31, 25, 30, 26, 28 деталей.
Выработка во второй бригаде: 27, 20, 56, 19, 18 деталей.
Исходные данные не сгруппированы, поэтому для расчёта средней выработки применяем среднюю арифметическую простую. Средняя дневная выработка рабочего:
в первой бригаде
во второй бригаде
Среднедневная выработка рабочего в обеих бригадах одинакова, но индивидуальные значения выработки во второй бригаде подвержены значительным колебаниям. Это вызывает необходимость измерять вариацию.
К абсолютным показателям вариации относятся
размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
В нашем примере размах вариации индивидуальной выработки:
в первой бригаде R1 =31-25=6 деталей
во второй бригаде R2 =56-18=38 деталей
Сравнение этих показателей свидетельствует о том, что размах вариации индивидуальной выработки во второй бригаде на 32 детали больше, чем в первой бригаде. Однако размах вариации не улавливает колеблемости вариантов внутри изучаемой совокупности. Для получения обобщающей характеристики колеблемости всех вариантов совокупности исчисляются другие показатели вариации.
Среднее линейное отклонение даёт обобщённую характеристику степени колеблемости признака в совокупности относительно среднего уровня признака и рассчитывается как средняя арифметическая из индивидуальных линейных отклонений по формуле:
– для невзвешенных данных 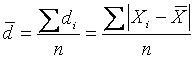
– для взвешенных данных 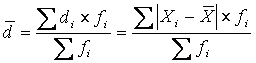
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируют состав работающих, ритмичность производства, равномерность поставок материалов; разрабатывают системы материального стимулирования. Но этот показатель усложняет расчёты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
В статистике дисперсия, центральный момент второго порядка, является оценкой одноимённого показателя теории вероятностей и оценкой дисперсии в математической статистике, что позволяет использовать теоретические положения этих дисциплин для анализа социально – экономических процессов. На дисперсии практически основаны все метод математической статистики. Большое значение имеет правило сложения дисперсий. Дисперсия рассчитывается как средний квадрат отклонений индивидуальных значений признака от среднего
значения признака по формуле:
– для невзвешенных данных 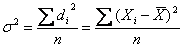
– для взвешенных данных 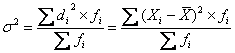
Для расчёта показателей вариации в нашем примере строим вспомогательную таблицу:
Индивидуальное линейное отклонение 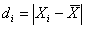
Относительные показатели вариации. Коэффициент осцилляции:



Коэффициент осцилляции:
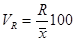
Для оценки меры вариации и ее значимости используют коэффициент вариации. Он получается путем сопоставления среднего линейного или среднего квадратического отклонения со средним уровнем явления и выражается в процентах:
Линейный коэффициент вариации:
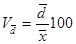
Коэффициент вариации:
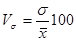
Относительные показатели вариации используются для:
1) сравнения колеблимости различных признаков в одной и той же совокупности;
2) при сравнении колеблимости одного и того же признака в нескольких совокупностях.
Значение коэффициента вариации изменяется от 0 до 1, и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности. Они дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.
Альтернативный признак – косвенный признак, имеющий две взаимоисключающие разновидности.
Альтернативные признаки принимают всего два значения:
1 – наличие признака;
0 – отсутствие признака.
Дисперсия альтернативного признака:
где p – доля единиц в совокупности, обладающих данным признаком;
q – доля единиц, не обладающих данным признаком.
Среднеквадратическое отклонение альтернативного признака:
Общая дисперсия –измеряет вариацию признака по всей совокупности от общей средней под влиянием всех факторов, обусловивших эту вариацию:
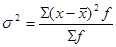
Межгрупповая дисперсияхарактеризует вариацию групповых средних от общей средней:
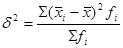
где 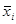
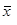
Внутригрупповая (частная) дисперсия отражает случайную вариацию, вариацию признака в группах от групповой средней:
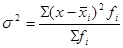
Средняя из внутригрупповых (частных) дисперсии:
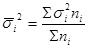
где 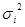
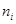
Между указанными видами дисперсий существует соотношение, которое называется правилом сложения дисперсий: общая дисперсия равна сумме средней из частных дисперсий и межгрупповой:
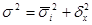
где 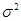
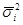
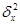
С помощью правила сложения дисперсий можно измерить силу влияния факторного признака, который положен в основу группировки, на результативный признак, вычислив коэффициенты детерминации и эмпирическое корреляционное отношение.
Эмпирический коэффициент детерминации показывает долю вариации результативного признака под влиянием факторного признака, равен отношению межгрупповой дисперсии к общей:
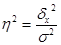
Эмпирическое корреляционное отношение показывает тесноту связи между группировочным и результативным признаками:
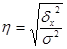
Эмпирическое корреляционное отношение варьирует в пределах от 0 до 1. При 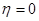
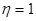
Правило сложения дисперсий для доли признака:
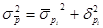
где 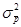
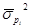
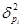
Общая дисперсия доли:
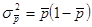
где 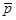
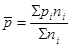
Средняя из групповых дисперсий доли:
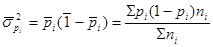
Межгрупповая дисперсия доли:
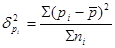
Вариация понятие, относительные и абсолютные показатели, способы их расчета
Этот термин ведёт своё происхождение от латинского слова «varito». Оно переводится как «изменение» или «различие».
Вариация это количественная мера изменения определённых данных, которая помогает исследовать её случайные изменения. Для их анализа применяют различные статистические методы.
О них будет более подробно рассказано в этой статье.
Онлайн-калькулятор показателей вариации
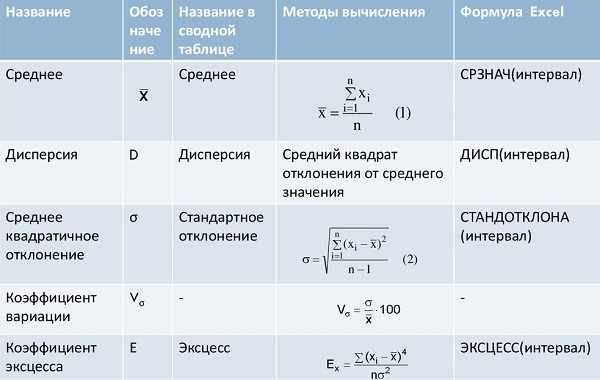
Показатели вариации в статистике
Статистика широко применяется в самых различных областях. Она доказала свою пользу не только в естественных науках, но и в изучении различных социологических явлений, изменений цен, а также в других ситуациях.
Эта наука имеет дело со случайными величинами, изменение которых требует для своего описания использования специальных характеристик. Наиболее известной из них является средняя. Однако, хотя она и включает в себя некоторый объём информации, тем не менее не даёт возможности найти информацию о разбросе случайных данных, а также дать понятие о динамике изменения и наиболее вероятных тенденциях в дальнейшем.
Математический аппарат для изучения вариационных процессов использует характеристики, способы расчёта которых можно разделить на три группы.
Показатели размаха изменений говорят о том, какова разница между максимальными отклонениями исследуемых чисел:
Данные, относящиеся ко второй категории, можно считать так:
Для расчёта относительных показателей применяется:
Далее будет рассказано о наиболее часто применяемых математических характеристиках рассматриваемого понятия.
При проведении статистических вычислениях удобно пользоваться электронными таблицами Excel.
Абсолютные показатели вариации
Когда говорят об абсолютных показателях вариации, имеют в виду следующие методы для проведения статистического анализа:
Размах вариации
При рассмотрении изменения исследуемых данных, одной из важных характеристик является размах вариации.
Он равен разности между максимальной и минимальной границами. Посмотрим, как это характеристика исчисляется.
Формула выглядит так:
РВар = ЗнМакс — ЗнМин,
Пример.
Эта формула может быть применена, например, в следующей ситуации. Предположим, рассматривается рост отобранных случайным образом людей. В этой совокупности десять человек и рост их равен: 165, 172, 179, 190, 182, 171, 191, 183, 177 и 178 сантиметров. Эти цифры составляют совокупность значений случайных данных.
Как можно увидеть в рассматриваемом случае, минимальный рост в этой группе людей составляет 165 см, а максимальный — 191 см. Разница между ними составляет 191 — 165 = 26 см. Таким образом, рассматриваемое значение для определённой таким образом совокупности данных показывает 26 см.
Отклонение вариации
Здесь рассматривается отклонение изучаемой случайной величины. Для того, чтобы его вычислить, необходимо сначала определить её среднее значение.
Чтобы посчитать, необходимо просуммировать все значения случайных данных и затем разделить на их количество. Получившаяся величина представляет собой нужный результат.
В некоторых формулах используются значения весов, придаваемых каждому значению. Кратко говоря, они назначаются в соответствии с целями проведения статистического исследования. Веса обычно подбираются таким образом, чтобы их сумма была равна единице.
Среднее линейное простое
Оценка величины отклонения рассчитывается так:
Формула выглядит таким образом:
СЛП = (|x(1) – x0| + |x(2) – x0| + … + |x(n) – x(0)|) / n,
Вертикальные чёрточки используются для того, чтобы показать, что здесь вычисляется абсолютная разность.
Среднее линейное взвешенное
Для этого потребуется формула:
СЛВ = (|x(1) – x0|*f(1) + |x(2) – x0|*f(2) + … + |x(n) – x(0)|*f(n)) / n,
Остальные обозначения рассмотрены ранее.
Среднее квадратическое отклонение
В этом случае результат определяется по другому правилу, чем в прежних случаях:
СКО = SQRT(((x(1) – x0)**2 + (x(2) – x0)**2 + … + (x(n) – x(0))**2) / n),
Дисперсия (простая, взвешенная)
Простая дисперсия равна СКО, возведённому в квадрат.
Взвешенная называется так потому, что каждое слагаемое умножается на свой вес.
Здесь применяется формула:
ДВ = (f(1)*(x(1) – x0)**2 + f(2)*(x(2) – x0)**2 + … + f(n)*(x(n) – x(0))**2) / n*(f(1) + f(2) + … + f(n)),
где: ДВ представляет собой дисперсию взвешенную.
Вариация альтернативного признака
Это понятие характеризует те ситуации, когда часть предметов выборки обладает определённым свойством, а другая — нет:
СРЕД = ((1-p) + (0-p)) / (p+q) = p,
ВАР = (q*(1-p)**2+ q*(0-p)**2) / (p+q) = pq.
Здесь СРЕД обозначает среднее, а p и q представляют собой положительные числа, в сумме дающие единицу.
ВАР обозначает искомую величину.
Относительные показатели вариации
В данном случае рассматриваются отношение отклонения и среднего конкретной выборки. Для различных характеристик используются различные способы определения среднего отклонения.
Чем меньше полученный коэффициент, тем более сгруппированы данные. Этот коэффициент не имеет единиц измерения.
Коэффициент осцилляции
Эта величина равна частному от деления размаха вариации на среднее случайной величины.
Коэффициент вариации
Такой коэффициент можно рассчитать путём деления линейного отклонения на такой же знаменатель, как в предыдущем случае.
Относительное линейное отклонение
В данном случае искомое значение рассчитывается как результат деления среднего квадратического на этот же знаменатель.
Примеры расчетов
Здесь будет приведены примеры расчётов. Рассматривается ситуация, когда пять человек устраиваются на новую работу. В данной специальности они проработали различное количество лет: 2, 3, 4, 7 и 9 лет.
X(0) = (2 + 3 + 4 + 7 + 9) / 5 = 25 / 5 = 5.
СЛП = (|x(1) – x0| + |x(2) – x0| + … + |x(n) – x(0)|)/n = (|2 5| + |3 5| + |4 5| + |7 5| + |9 – 5|) / 5 = (3 + 2 + 1 + 2 + 4) / 5 = 12 / 5 = 2,4 года.
СКО = SQRT(((x(1) – x0)**2 + (x(2) – x0)**2 + … + (x(n) – x(0))**2)/n) = SQRT(((2 – 5)**2 + (3 – 5)**2 + (4 – 5)**2 + (7 – 5)**2 + (9 – 5)**2) / 5) = SQRT((3**2 + 2**2 + 1**2 + 2**2 + 4**2)/5) = SQRT ((9 + 4 + 1 + 4 + 16) / 5) = SQRT(34 / 5) = SQRT(6,80) = 2,61 года (приблизительное значение).
Последнее значение равно СКО, возведённому в квадрат.
В большинстве случаев расчет представляет собой гораздо более сложную задачу, чем показано в приведённом примере. Для облегчения процесса вычислений можно использовать онлайн калькулятор.
Заключение
Изучение случайных процессов играет важную роль в науке, экономике и общественной жизни. Для того, чтобы получить максимальное количество информации при их изучении, нужно активно использовать статистические методы, в том числе те, которые связаны с вариацией.