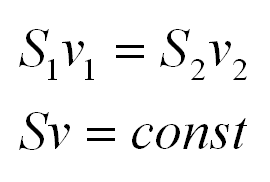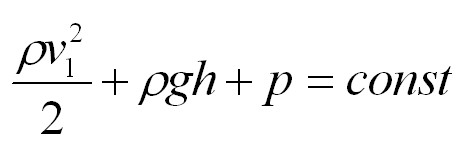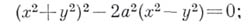кривая бернулли что это такое
Что означает кривая Бернулли на гербе бухгалтеров?
Мы знаем, что есть гербы у городов, государств, династий, воинских подразделений. А вы в курсе, что у некоторых профессий тоже есть геральдические символы? Не все они, конечно, понятны и однозначны с первого взгляда. Например, что означает кривая Бернулли на гербе бухгалтеров? Давайте разберемся!
Бухгалтерский герб
Автором данного геральдического символа стал француз Ж.-Б. Дюмарше. Ученый был одним из известных представителей бухгалтерской науки. Представил публике свое творение в 1944 году. Затем Всемирной академией бухгалтерских работников знак был признан символом всех представителей этой скрупулезной счетной профессии.

Что любопытно, слова SCIENCE-CONSCIENCE-INDEPENDANCE переводятся одинаково и с французского, и с английского языка. Но некоторые трактуют девиз и иначе. Отметим, что CONSCIENCE с французского на русский может также переводится как «добросовестность», «сознание», «доверие».

Значение символики
Перейдем к предметам на гербе и, в частности, к кривой Бернулли:
Сам же автор, Жан-Батист Дюмарше, эти символы трактовал несколько по-иному:
А вот сами бухгалтеры придумали несколько иную, ироническую трактовку и символов герба, и его девиза. Хотите посмотреть на это взглядом изнутри? Читайте далее!
Что означает кривая Бернулли?
По альтернативному мнению, кривая Бернулли выступает символом запутанности, крючкотворства, сознательной усложненности. Она непонятна зрителю, как и непосвященному человеку вся бухгалтерская наука. Бухгалтеры с чувством юмора подчеркивают именно слово «кривая». А не прямая, которая бы означала бескомпромиссность, прямолинейность, правильный путь.
Проведем небольшое исследование этого загадочного символа. Дюмарше приписывает его авторство математику Якобу Бернулли. Если мы изучим его труды, то заметим среди них только одну кривую. Она называется Лемниската Бернулли и графически представляет собой всем известный символ бесконечности.
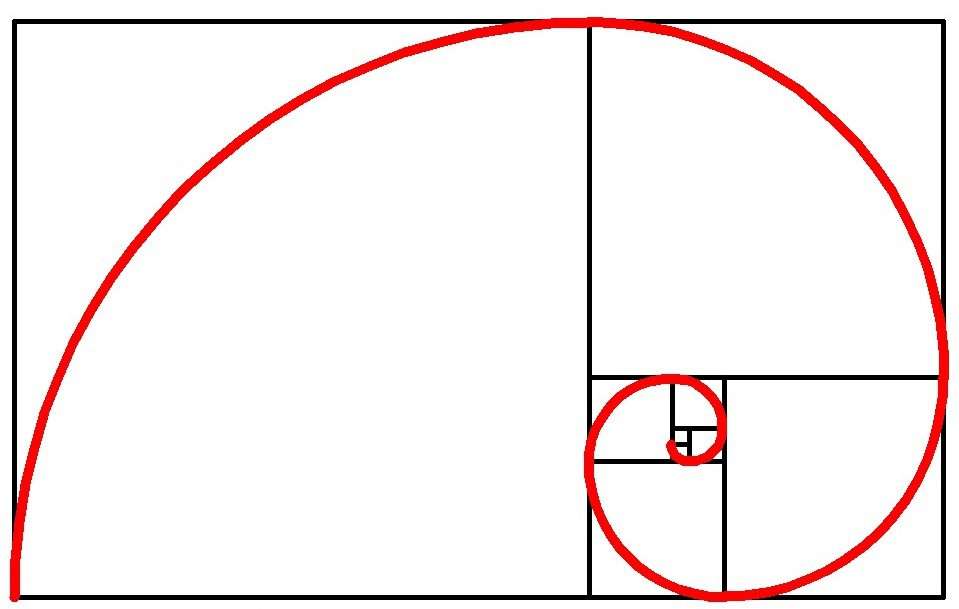
Так что же такое кривая Бернулли? Скорее всего, это один из частных случаев логарифмической спирали, названный спиралью Фибоначчи. Для бухгалтерии важно и имя этого ученого, ведь именно он способствовал распространению арабских цифр и десятичной системы счисления, без чего трудно представить современный учет.
Что означает солнце?
Также некоторые считают, что на эмблеме изображена не самая близкая к нам звезда, а ослепительно сверкающая золотая монета. Ведь солнечный свет визуально белый, а не желтый, как на эмблеме.
Что означают весы?
А вот весы воспринимаются не в качестве символа баланса, а как атрибут богини правосудия Фемиды, изображающейся с завязанными глазами. А что это может значить? При допущении ошибки в работе судьба бухгалтера вполне может оказаться на этих весах!
Некоторые представители профессии шутят, что пока глаза Фемиды завязаны, бухгалтерский отдел может спать спокойно.
Что означает фоновый цвет?
Что означает форма герба?
Сегодня часто встречается круглая форма геральдического бухгалтерского символа. Однако обратим ваше внимание на то, что исконно она все-таки была овальной. Форма напоминала «0». А именно эта цифра выступает символом устойчивости.
Альтернативная трактовка девиза
Бухгалтеры сегодня критикуют свой слоган:
Какое значение имеет кривая Бернулли на гербе бухгалтеров?
Мы знаем, что есть гербы у городов, государств, династий, воинских подразделений. А вы в курсе, что у некоторых профессий тоже есть геральдические символы? Не все они, конечно, понятны и однозначны с первого взгляда. Например, что означает кривая Бернулли на гербе бухгалтеров? Давайте разберемся!
Бухгалтерский герб
Автором данного геральдического символа стал француз Ж.-Б. Дюмарше. Ученый был одним из известных представителей бухгалтерской науки. Представил публике свое творение в 1944 году. Затем Всемирной академией бухгалтерских работников знак был признан символом всех представителей этой скрупулезной счетной профессии.
Что любопытно, слова SCIENCE-CONSCIENCE-INDEPENDANCE переводятся одинаково и с французского, и с английского языка. Но некоторые трактуют девиз и иначе. Отметим, что CONSCIENCE с французского на русский может также переводится как «добросовестность», «сознание», «доверие».
Значение символики
Перейдем к предметам на гербе и, в частности, к кривой Бернулли:
Сам же автор, Жан-Батист Дюмарше, эти символы трактовал несколько по-иному:
А вот сами бухгалтеры придумали несколько иную, ироническую трактовку и символов герба, и его девиза. Хотите посмотреть на это взглядом изнутри? Читайте далее!
Что означает кривая Бернулли?
По альтернативному мнению, кривая Бернулли выступает символом запутанности, крючкотворства, сознательной усложненности. Она непонятна зрителю, как и непосвященному человеку вся бухгалтерская наука. Бухгалтеры с чувством юмора подчеркивают именно слово «кривая». А не прямая, которая бы означала бескомпромиссность, прямолинейность, правильный путь.
Проведем небольшое исследование этого загадочного символа. Дюмарше приписывает его авторство математику Якобу Бернулли. Если мы изучим его труды, то заметим среди них только одну кривую. Она называется Лемниската Бернулли и графически представляет собой всем известный символ бесконечности.
Так что же такое кривая Бернулли? Скорее всего, это один из частных случаев логарифмической спирали, названный спиралью Фибоначчи. Для бухгалтерии важно и имя этого ученого, ведь именно он способствовал распространению арабских цифр и десятичной системы счисления, без чего трудно представить современный учет.
Что означает солнце?
Также некоторые считают, что на эмблеме изображена не самая близкая к нам звезда, а ослепительно сверкающая золотая монета. Ведь солнечный свет визуально белый, а не желтый, как на эмблеме.
Что означают весы?
А вот весы воспринимаются не в качестве символа баланса, а как атрибут богини правосудия Фемиды, изображающейся с завязанными глазами. А что это может значить? При допущении ошибки в работе судьба бухгалтера вполне может оказаться на этих весах!
Некоторые представители профессии шутят, что пока глаза Фемиды завязаны, бухгалтерский отдел может спать спокойно.
Что означает фоновый цвет?
Что означает форма герба?
Сегодня часто встречается круглая форма геральдического бухгалтерского символа. Однако обратим ваше внимание на то, что исконно она все-таки была овальной. Форма напоминала «0». А именно эта цифра выступает символом устойчивости.
Альтернативная трактовка девиза
Бухгалтеры сегодня критикуют свой слоган:
Закон Бернулли для чайников и учёных
Предисловием можно считать «За что физики не любят математиков»: http://proza.ru/2015/11/16/160
«Наука должна быть весёлая, увлекательная и простая. Таковыми же должны быть и учёные» (П.Л. Капица). и преподаватели. Но более всего наука должна быть честная. И «Ни один человек не должен покидать стены наших университетов без понимания того, как мало он знает» (Роберт Оппенгеймер). и как мало знают учёные. А чтобы так оно и было, нужно срезать профессора математической лженауки на первой же лекции. И прежним занудой он уже не будет. Знаю, что говорю, и привожу очередной пример.
Правильный ответ: неподвижные поверхностные манометры на картинке вверху показывают давление потоков, так как для измерения давления в потоках нужны такие манометры или датчики давления, которые находились бы внутри потоков и двигались вместе с ними. Давление внутри потоков, знаете ли, почти всегда статично. Но таких мобильных манометров, которые могли бы быть неподвижными относительно ламинарных потоков, нет в опытах к теме «Закон Бернулли». Однако вывод сделан такой, словно они есть, словно давление внутри потоков уже измерено. «Для физика должно существовать только то, что измерено» (Нильс Бор). а не то, что можно подумать, придумать, недодумать и сосчитать. Сосчитать то, чего нет, может каждый.
А тем-то он и хуже, что никакой научности и сложности для понимания в нём нет. К тому же, давление потока на поперечную поверхность или «скоростной напор» измеряется с помощью Г-образной «трубки Пито», вставляемой в поток загнутым концом навстречу потоку. Отсюда: давление в самом потоке примерно равно среднему арифметическому от показаний «трубки Пито» и «трубки у Бернулли». Более того, в ньютоновской механике уменьшение силы давления на параллельную потоку или телу поверхность с увеличением скорости потока или тела и одновременное увеличение давления потока или тела на поперечную поверхность можно объяснить простым векторным разложением силы давления потока или тела. Чем больше скорость автомобиля, тем меньше его вес и давление на дорожное полотно; чем больше скорость потока, тем меньше его давление на стенки трубы. Пусть пока будет так.
Конечно, наши выводы профессору будут сильно не по нутру. Но если он будет ещё в состоянии что-то говорить и продолжит настаивать на том, что «С увеличением скорости потока давление внутри потока уменьшается», то срежем его вторым вопросом: «Почему причина и следствие в формулировке общепризнанного закона Бернулли переставлены местами?».
Можно короче: «Чем больше падение давления в потоке или на данном участке трубы, тем больше здесь и скорость самого потока». И это будет тривиальный закон потоков, у которого уже есть все пять обязательных признаков новой истины: простота, ясность, универсальность, «предсказательная сила» и антинаучность. Опровергнуть этот закон сможет только тот, кто создаст поток жидкости или газа, движущийся из области пониженного давления в область повышенного давления, то есть против действия превосходящих сил давления и упругости. Шутка.
Инженер-аэродинамист сформулирует свой закон потоков примерно так: «Давление потока на параллельную или отрицательно наклонную поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока или поверхности (верхней поверхности крыла); а давление потока на поперечную или положительно наклонную поверхность всегда тем больше давления в самом потоке, чем больше скорость потока или поверхности (нижней поверхности атакующего крыла)». И это будет качественный закон взаимодействия потоков с поверхностями, так как в каждом конкретном случае величина давления потока на поверхность зависит не только от скорости потока, но и от физических свойств потока и поверхности, поэтому она не вычисляется, а только измеряется. Следовательно, математикам и в аэродинамике делать особо нечего.
Действие этих двух законов во многих опытах и явлениях складывается или накладывается, поэтому наблюдаемый результат нельзя объяснять действием только какого-то одного закона. Но объединённого закона Бернулли или третьего математического закона потоков никогда не было, поэтому как определить «личную долю» каждого закона в результате того или иного опыта к теме «Закон Бернулли» не знает ни один математик. но знает каждый инженер. Он просто измеряет с помощью манометров и динамометров давление в потоке и давление потока при различной скорости потока, а потом лишь сравнивает результаты измерений. и никаких теорий потоков для него словно не существует. Действительно, зачем вычислять, если можно измерить.
Качественный закон потоков гласит: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». Можно короче: «Давление потока на параллельную поверхность всегда тем меньше, чем больше хаос в движении частиц потока».
В гидродинамике давление всегда первично, а скорость потока вторична; в аэродинамике скорость крыла всегда первична, а давление неподвижной атмосферы на него всегда вторично. Плоское крыло самолёта или птицы не изменяет давление в неподвижной атмосфере, а изменяется с увеличением скорости и угла атаки лишь взаимодействие быстрого крыла с атмосферой. Но в наших рассуждениях крыло чаще всего неподвижно, а это атмосфера «набегает» на крыло, словно всё происходит в аэродинамической трубе или в статическом (стационарном) потоке. Просто так нам удобнее рассуждать и объяснять.
У инженеров всё, что летает, делает это по причине совсем небольшой положительной разницы или асимметрии атмосферного давления на крыло. Появление подъёмной силы как раз и обусловлено качественным законом потоков: «Давление атмосферного потока на верхнюю отрицательно наклонную поверхность быстрого крыла тем меньше давления в самой атмосфере, чем больше хаос и разрежение частиц воздуха над ней; а давление потока на нижнюю положительно наклонную поверхность крыла тем больше атмосферного давления, чем больше скорость крыла, его угол наклона или атаки и деформация или уплотнение упругого воздуха под быстрым крылом». Как диагональ делит прямоугольник на два равных треугольника, так и плоское атакующее крыло делит набегающий поток на две самостоятельные и равнозначные причины возникновения подъёмной силы.
Вспомним, атмосферное давление на уровне моря равно 1,0033 кг/см2. Это очень большая сила, которая давит на неподвижное плоское крыло совершенно одинаково и сверху, и снизу. Если атмосферное давление со стороны одной из поверхностей крыла убрать, то со стороны противоположной поверхности тут же возникнет сила равная 10033 кг/м2. Да, 10 тонн на каждый квадратный метр крыла! И что мы имеем: орёл весом 4 кг, имея площадь «несущих поверхностей» как раз 1м2, почти неподвижно парит в вышине при положительной разнице атмосферных давлений на его крылья всего 0,04% от теоретически возможного 1 кг/см2; АН-2 («кукурузник») летает горизонтально на разности 0,4% атмосферного давления; а скоростному современному пассажирскому авиалайнеру для горизонтального полёта достаточно и 5% от 1 кг/см2 или 50 г/см2.
Идеальный или самый эффективный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло. И это для передовых инженеров уже аксиома или «новая аэродинамика», а Природа это знала ещё со времён первых летающих насекомых и птеродактилей. Так вот, асимметричное атмосферное давление на совершенно плоское крыло возникает и при его нулевом угле наклона к вектору движения набегающего атмосферного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая. В воде «эффект хаоса над крылом» проявляется ещё значительно сильнее.
Это утверждение доказано самой эволюцией живой природы и передовой практикой авиастроения. Смотрим на расправленное крыло любой птицы: сверху оно бархатистое и может играть всеми цветами радуги, что физику говорит о дисперсии света на мельчайших неровностях на поверхности, а снизу – всегда очень плотное, гладкое и со стальным отливом. Смотрим на современный пассажирский «Боинг»: сверху он словно матовый, а снизу – зеркально гладкий. И пусть та положительная разница в атмосферном давлении на крыло, которая возникает только по причине различного качества покрытия его аэродинамических поверхностей, будет и недостаточной для полёта, но именно она и позволит самолёту или птице лететь горизонтально с меньшим углом атаки, то есть с меньшим лобовым сопротивлением, экономя топливо и силы.
Инженеры «Боинга» говорят, что уже экономят на «эффекте хаоса над крылом» до 7-ми процентов топлива, а это огромные деньги. Смотрите фотографии «Боингов» и читайте по запросу «Аэродинамика Боинг». А наши дурни из Сколково одной краской покрывают весь Боинг. Смотрите по запросу «Красим Боинг». Кожа акулы тоже только кажется гладкой, а на ощупь она сравнима с наждачной бумагой. Шершавая кожа способствует образованию хаоса в пограничном слое воды, что ещё больше уменьшает её давление на быструю акулу. И таких примеров «мильён».
Однако вторым законом потоков объясняются не только опыты к теме «Закон Бернулли», но ещё один раз доказывается нечто совсем другое, позволяющее увидеть истоки математического идеализма в физике и похоронить математическую физику, как науку о природе. «Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру» (А. Эйнштейн). Сейчас мы эту словесную формулу математического идеализма просто-напросто докажем. Вернее, я докажу, а вы. согласитесь.
«Все жидкости и газы на Земле имеют вес и находятся под давлением веса собственных и выше расположенных слоёв» (Архимед). Поэтому все прозрачные жидкости и газы состоят из примерно одинаковых, равноудалённых и условно неподвижных (колеблющихся или дрожащих) частиц, находящихся в состоянии взаимного отталкивания и относительного (или чуткого) равновесия и взаимно отталкивающихся в газах на расстояниях много больших, чем в жидкостях. Отсюда: давление в любой точке водоёма или атмосферы равно напряжению взаимного отталкивания равноудалённых частиц в этой точке, и по силе оно равно весу всех частиц над этой точкой. Уберите атмосферное давление, и капля воды тут же исчезнет, разлетевшись на молекулы, а аквариум с водой словно взорвётся. И повинно в том будет как раз-таки «напряжение взаимного отталкивания равноудалённых частиц». Смотрите по запросу «Современный Архимед. Трактат «О плавающих телах» и «К физике антигравитонов». Там есть опыты, позволяющие буквально увидеть неподвижность колеблющихся частиц в жидкостях и в газах. Особенно показателен опыт по мгновенному замерзании переохлаждённой воды при её встряхивании в пластиковой бутылке. Многие его знают, но не понимают.
Способность атомов и молекул к движению взаимного отталкивания пропорциональна температуре. А температура – это «опосредованное мерило» интенсивности атомных и внутриатомных движений и величины гравитационных моментов (квантов, импульсов) атомов, передающихся от атома к атому путём индукции.
И ещё. Всем теоретикам и преподавателям на засыпку: «Какой теорией руководствовались братья Райт, когда делали свой воздушный винт, который у них получился с КПД 78-80%, если научной аэродинамики ещё не было, а КПД самых современных пропеллеров из дерева не превышает 85%?».
Хотелось бы услышать возражения или замечания, но их почему-то нет. Видимо, с тем, что мы живём в эпоху математических лженаук, уже никто не спорит.
Воображеньем прозорливым
К догадкам верным нас несло…
Но сонм учёных кропотливых
Свернул наш поиск — на число.
И лязгом счёта оглушённый
Забыл наш ум — решенья ключ…
Стал слепнуть, в шоры цифр втеснённый.
А был так зряч и так могуч!
Уж цифре памятник построен,
Распята Истина на нём.
Поклонник счёта, жрец и воин
Простёрся ниц перед числом:
Не осознать бедняге в заблужденье,
Как много лжи за ширмой исчисленья!
Течение жидкости и уравнение Бернулли для новичков
Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».
Кто такой Бернулли?
Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».
Д. Бернулли (1700-1782)
Идеальная жидкость и течение идеальной жидкости
Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.
Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.
Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.
Поток жидкости– совокупность частиц движущейся жидкости.

Вывод уравнения Бернулли
Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.
Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2. При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.
Данное уравнение – уравнение неразрывности струи.
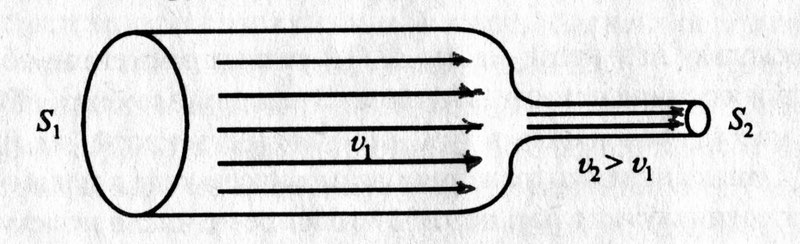
Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:
Смысл уравнения Бернулли
Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.
Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.
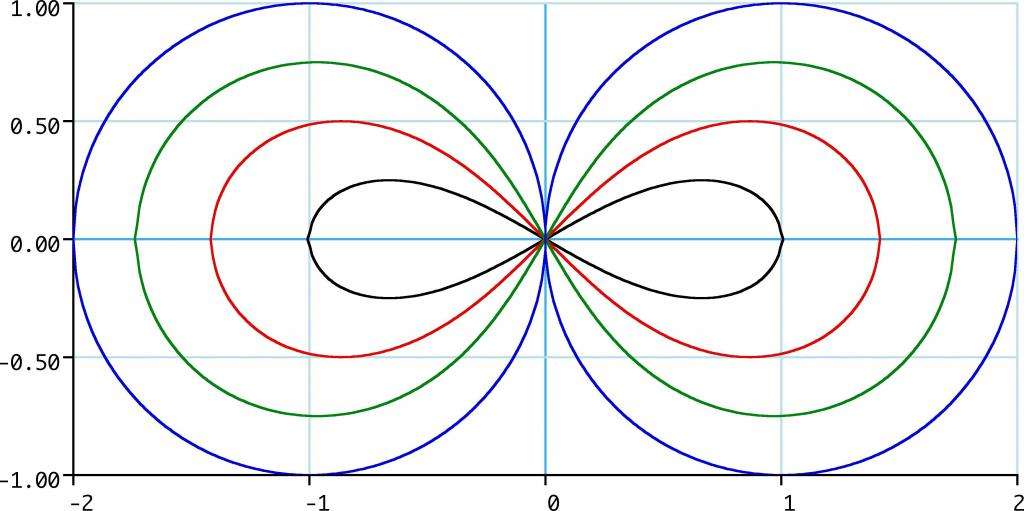
БЕРНУЛЛИ ЛЕМНИСКАТА
— плоская алгебраич. кривая 4-го порядка, уравнение к-рой в декартовых прямоугольных координатах имеет вид:
в полярных координатах
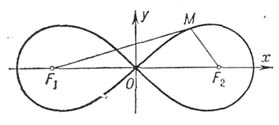
Б. л. симметрична относительно начала координат О(см. рис.), к-рое является узловой точкой с касательными 

Произведение расстояний каждой точки МБ. л. до двух данных точек 

Б. л. названа по имени Я. Бернулли (J. Bernoulli), в статье к-рого впервые встречается уравнение этой кривой (1694).
Лит.:[1] Саве лов А. А., Плоские кривые, М., 1960.
Смотреть что такое «БЕРНУЛЛИ ЛЕМНИСКАТА» в других словарях:
Лемниската Бута — Лемниската Бута плоская алгебраическая кривая четвёртого порядка, частный случай кривой Персея. Названа в честь Джеймса Бута. Уравнение в прямоугольных декартовых координатах … Википедия
Лемниската Бернулли — Лемниската и её фокусы Лемниската Бернулли плоская алгебраическая кривая. Определяется как геометрическое место точек, произведени … Википедия
Лемниската Жероно — плоская кривая, удовлетворяющая уравнению … Википедия
ЛЕМНИСКАТА Бернулли — (от лат. lemniscatus, буквально украшенный лентами), плоская кривая, имеющая вид восьмерки; множество точек M, произведение расстояний r1 и r2 которых до двух данных точек F1, F2 (фокусов) равно квадрату междуфокусного расстояния. Алгебраическая… … Энциклопедический словарь
ЛЕМНИСКАТА Бернулли — (от лат. lemniscatus буквально украшенный лентами), плоская кривая, имеющая вид восьмерки; множество точек M, произведение расстояний r1 и r2 которых до двух данных точек F1, F2 (фокусов) равно квадрату междуфокусного расстояния. Алгебраическая… … Большой Энциклопедический словарь
ЛЕМНИСКАТА — (греч., от lemniskos лента). В геометрии кривая линия четвертой степени, имеющая форму цифры 8. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЛЕМНИСКАТА в геометрии кривая линия, имеющая форму цифры 8. Словарь… … Словарь иностранных слов русского языка
ЛЕМНИСКАТА — Бернулли (от лат. lemniscatus, буки. украшенный лентами), плоская кривая, имеющая вид восьмёрки (рис.); множество точек М, произведение расстояний r1и r2 к рых до двух данных точек F1, F2(фокусов) равно квадрату междуфокусного расстояния. Алгебр … Естествознание. Энциклопедический словарь
Бернулли (семья) — У этого термина существуют и другие значения, см. Бернулли. Семья Бернулли (Bernoulli) швейцарская протестантская семья, многие члены которой в XVII XVIII веках внесли существенный вклад в науку. В частности, к этой династии принадлежат 9… … Википедия
Бернулли, Якоб — Якоб Бернулли Jakob Bernoulli … Википедия