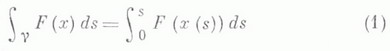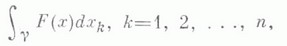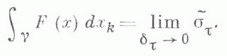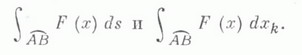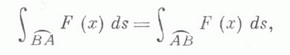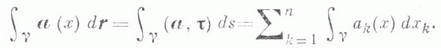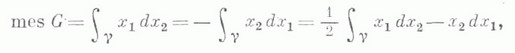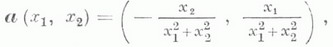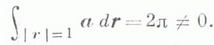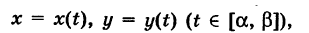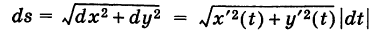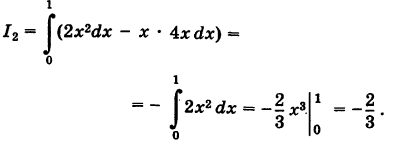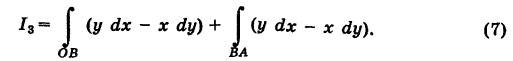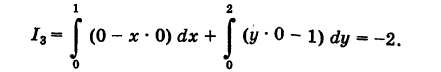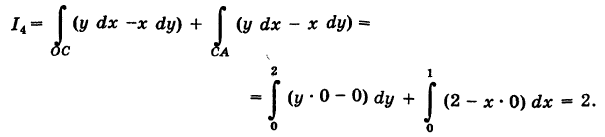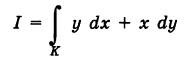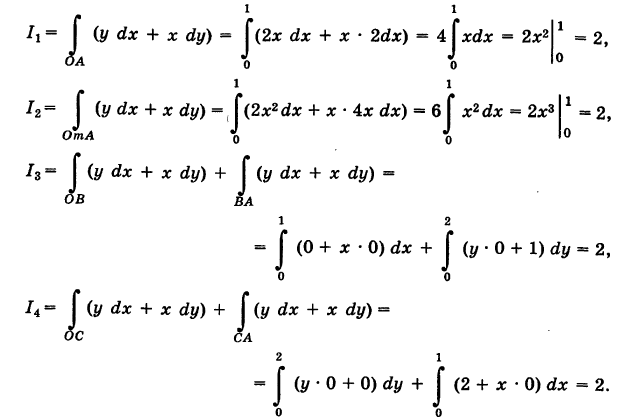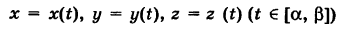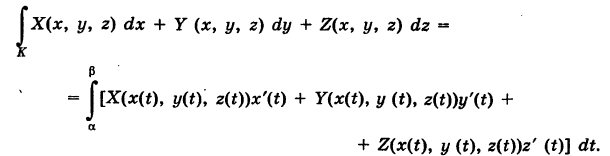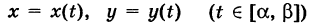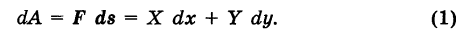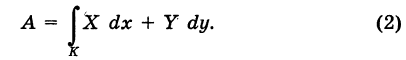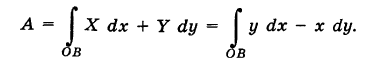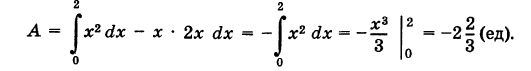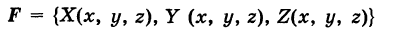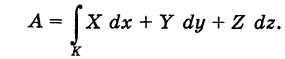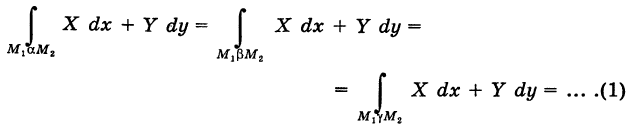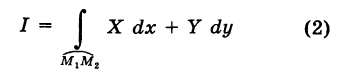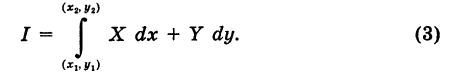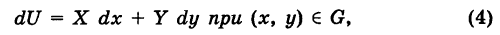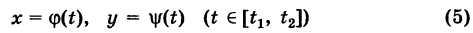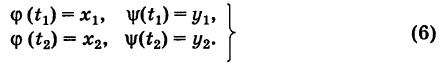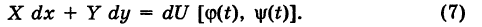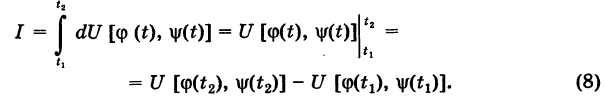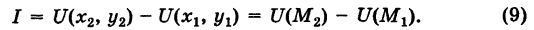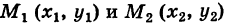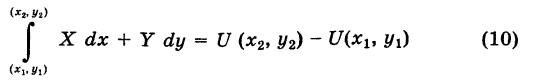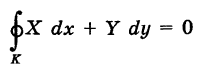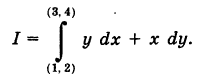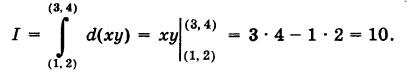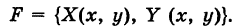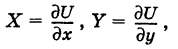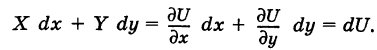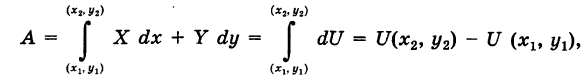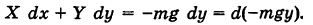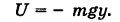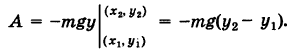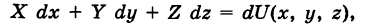криволинейный интеграл что это

Криволинейный интеграл

Главная > Учебные материалы > Математика: Криволинейный интеграл

1.Криволинейный интеграл 1-го рода. 2.Свойства криволинейного интеграла 1-го рода. 3.Криволинейный интеграл 2-го рода. 4.Свойства криволинейного интеграла 2-го рода.

1.Криволинейный интеграл 1-го рода.

Пусть на плоскости Оxy задана функция материальной кривой f (x) рис.1. В каждой точке кривой f (x) АВ определена линейная плотность масс этой кривой. Линейная плотность материальной кривой в каждой точке N ( N∈ab ) равна ординате точки N (x;y), т.е. ρ(N) = y. Линейной плотностью дуги кривой называется предел отношения массы к длине дуги кривой, т.е.

где

Если взять предел последнего выражения, то можно рассчитать точное значение массы кривой.

то этот предел называется криволинейным интегралом первого рода от функции f ( x; y ).

Криволинейный интеграл обозначается:

Для вычисления криволинейного интеграла первого рода используется формула сведения его к определенному интегралу.

Допустим кривая АВ задана параметрически, т.е.

Тогда криволинейный интеграл рассчитывается по формуле:

Если кривая АВ задана явным уравнением вида y = f (x), то формула для рассчета будет иметь следующий вид:

2.Свойства криволинейного интеграла 1-го рода.

1. Величина интеграла не зависит от направления на дуге, т.е.

2.В случае, если дуга АВ состоит из двух частей АС и СВ, то

3.Криволинейный интеграл 2-го рода.

то этот предел называется криволинейным интегралом 2-го рода по кривой АВ.

Допустим, что на кривой АВ определены две функции P (x,y) и Q (x,y) и существуют интегралы

тогда сумма этих интегралов называется полным криволинейным интегралом 2-го рода.

Криволинейный интеграл 2-го рода рассчитывается по формуле:

Если кривая АВ задана явно, т.е. y = f (x), то формула примет вид:

4.Свойства криволинейного интеграла 2-го рода.

1. Если меняется направление обхода кривой АВ, то интеграл меняет знак.

2.Если кривая АВ состоит из частей, то полный интеграл равен сумме интегралов каждой части.

Источник

КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ

интеграл по кривой. Пусть в тг-мерном евклидовом пространстве 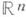задана спрямляемая кривая — длина дуги и на кривой g задана функция F=F(x(s)). К. и.

К. и. первого рода не зависит от ориентации кривой:

а К. и. второго рода меняет знак при изменении ориентации кривой:

и тем самым интегралы, стоящие в правой части этих равенств, не зависят от выбора параметра на кривой g. Если — единичный касательный вектор к кривой g, то К. н. второго рода выражается через К. и. первого рода по формуле

Если кривая g задана векторным представлением 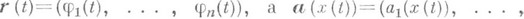— векторная функция, определенная на g, то, по определению,

Связь между К. и. и интегралами других видов устанавливается Грина формулой и Стокса формулой.

С помощью К. и. можно вычислять площади плоских областей: если конечная плоская область Gограничена спрямляемым простым контуром g, то ее площадь равна

Если F(х) — напряженность силового поля (т. е. сила, действующая на единицу массы), тогда

равен работе силового поля вдоль кривой Y при перемещении вдоль g единичной массы. К. и. используются в теории векторных полей. Если непрерывное векторное поле определено на нек-рой л-мерной области G, n>1, то следующие три свойства эквивалентны.

1) Для любой замкнутой спрямляемой кривой 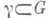справедливо равенство (векторное поле, обладающее этим свойством, наз. потенциальным).

2) Для любой пары точек и для любых двух спрямляемых кривых с началом в точко Аи концом в точке В:

3) В области Gсуществует такая функция и(х).(называемая потенциальной функцией векторного поля а(х)), что т. е. при этом для любых и любой кривой

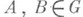
4) Вихрь векторного поля в области G равен нулю:

определенного на плоскости с выброшенным началом координат, имеем но

Лит.:[1] Ильин В. А., П о з н я к Э.

Полезное

Смотреть что такое «КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ» в других словарях:

КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ — интеграл от функции, заданной вдоль какой либо кривой на плоскости или в пространстве. Его можно свести к определенному интегралу, а при некоторых дополнительных условиях к двойному интегралу (Грина формула) или поверхностному интегралу (Стокса… … Большой Энциклопедический словарь

Криволинейный интеграл — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Криволинейн … Википедия

криволинейный интеграл — интеграл от функции, заданной вдоль какой либо кривой на плоскости или в пространстве. Его можно свести к определённому интегралу, а при некоторых дополнительных условиях к двойному интегралу (Грина формула) или поверхностному интегралу (Стокса… … Энциклопедический словарь

криволинейный интеграл — kreivinis integralas statusas T sritis fizika atitikmenys: angl. curvilinear integral; path integral vok. Kurvenintegral, n rus. криволинейный интеграл, m pranc. intégrale curviligne, f … Fizikos terminų žodynas

Криволинейный интеграл — интеграл, взятый вдоль какой либо кривой на плоскости или в пространстве. Различают К. и. 1 го и 2 го типов. К. и. 1 го типа возникает, например, при рассмотрении задачи о вычислении массы кривой переменной плотности; он обозначается… … Большая советская энциклопедия

КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ — интеграл от функции, заданной вдоль к. л. кривой на плоскости или в пространстве. Его можно свести к определ. интегралу, а при нек рых дополнит. условиях к двойному интегралу (Грина формула) или поверхностному интегралу (Стокса формула) … Естествознание. Энциклопедический словарь

Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия

ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… … Математическая энциклопедия

ГИЛЬБЕРТА ИНВАРИАНТНЫЙ ИНТЕГРАЛ — криволинейный интеграл от замкнутой дифференциальной формы, являющейся производной действия функционала вариационного исчисления. Для функционала ищется вектор функция наз. полем, так, чтобы интеграл не зависел от пути интегрирования. Если такая… … Математическая энциклопедия

Поверхностный интеграл — интеграл от функции, заданной на какой либо поверхности. К П. и. приводит, например, задача вычисления массы, распределённой по поверхности S с переменной поверхностной плотностью f (M). Для этого разбивают поверхность на части s1, s2 … Большая советская энциклопедия

Источник

Содержание:

Криволинейные интегралы

Криволинейный интеграл первого рода

Пусть К — некоторая гладкая (или кусочно-гладкая) плоская кривая

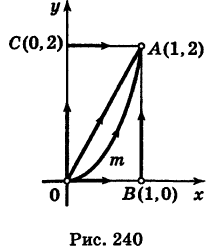
3) На основании свойства 2 имеем

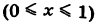
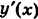
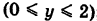
Так как уравнение ОВ есть у = 0 , то = 0. Далее, уравнение ВА записывается так: х = 1 ; поэтому х'(у) = 0. Из формулы (7) получаем

Заметим, что здесь интеграл I при фиксированных концах пути интегрирования К зависит от вида этого пути.

Пример:

вдоль линий К, указанных в примере 1.

Воспользовавшись приведенными выше уравнениями линии К, последовательно имеем:

Таким образом, здесь интеграл I имеет одно и то же значение для различных путей, соединяющих точки О и А. Принципиальное различие примеров 1 и 2 будет разъяснено. Если

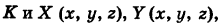
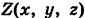
есть кусочно-гладкая пространственная кривая — тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл

Физический смысл криволинейного интеграла второго рода

Пусть 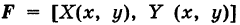— непрерывно меняющаяся переменная сила и

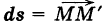
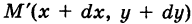
— путь К, пробегаемый точкой ее приложения (рис. 241); обозначим через бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку (мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = . Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна

Интегрируя выражение (1) вдоль кривой К, получим работу силы

Выражение (2), очевидно, есть соответствующий криволинейный интеграл второго рода.

Итак, криволинейный интеграл второго рода представляет собой работу переменной силы вдоль пути интегрирования, проекциями которой на координатные оси являются соответствующие коэффициенты при дифференциалах переменных.

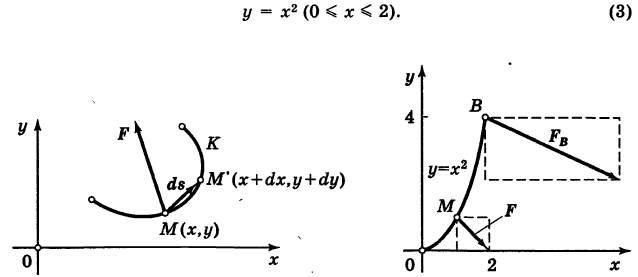
Пример:

Найти работу А переменной силы 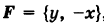, точка приложения которой описывает параболу ОВ (рис. 242)

Решение:

Согласно формуле (2) имеем

Из уравнения (3) получаем dy = 2х dx, поэтому

Аналогично, работа пространственной силы

вдоль пути К: 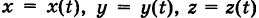выражается криволинейным интегралом второго рода

Условие независимости криволинейного интеграла второго рода от вида пути интегрирования

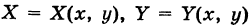
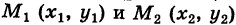
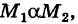
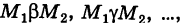
Пусть — непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки области и всевозможные пути соединяющие эти точки (М₁ — начало пути, М₂ — конец пути) и не выходящие за пределы области G. Может случиться, что

В таком случае говорят, что криволинейный интеграл второго рода

не зависит от вида пути интегрирования в данной области G.

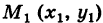
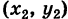
Если выполняются условия (1), то для интеграла (2) нет необходимости указывать путь интегрирования, а достаточно отметить лишь его начальную точку и его конечную точку М₂ пути. Поэтому здесь употребляется обозначение

Справедлива следующая теорема:

Теорема: Если в области G подынтегральное выражение X dx + Y dy является полным дифференциалом некоторой функции U = U (х, у), т. е.

то криволинейный интеграл (2) не зависит от пути интегрирования в области G.

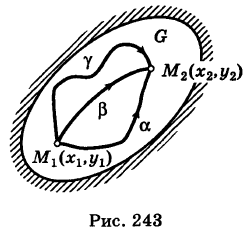
Доказательство: Пусть

— произвольный путь К в области G, соединяющий точки 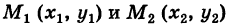, причем

Из формулы (4) имеем

Далее, используя соотношения (6), будем иметь

Таким образом, значение интеграла I одно и то же при любом выборе функций 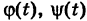, и, следовательно, интеграл I не зависит от вида пути, соединяющего точки

Следствие 1. Если выполнено соотношение (4), то в силу (9) имеем

(обобщенная формула Ньютона — Лейбница).

Следствие 2. Если подынтегральное выражение X dx + Y dy есть полный дифференциал и путь интегрирования К замкнутый, то

(кружок при интеграле обозначает интегрирование вдоль замкнутого пути).

Пример:

Решение:

Так как у dx + х dy = d (ху), то, независимо от вида пути, соединяющего точки 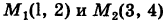, имеем

Работа потенциальной силы

Теорема предыдущего параграфа имеет физическое содержание. Пусть в области G определено силовое поле

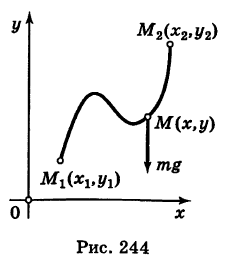
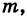
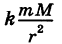
Примером силового поля может служить поле силы тяжести у поверхности Земли, где на любую материальную точку массы т действует сила mg (g — ускорение свободного падения). Более общим примером силового поля является гравитационное поле, создаваемое массой М. Здесь на материальную точку массы находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила (k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.

Если существует функция 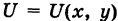такая, что

то говорят, что поле потенциальное (иначе, F — потенциальная сила), а функцию U называют потенциалом поля. В этом случае, очевидно,

Отсюда для работы А потенциальной силы F вдоль пути, соединяющего точки 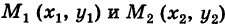, имеем

т. е. работа потенциальной силы не зависит от вида пути и равна разности потенциалов силы для конечной и начальной точек пути.

В частности, если путь замкнут, то работа А = 0.

Пример:

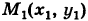
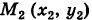
Найти работу А силы тяжести при перемещении в вертикальной плоскости Оху (вблизи поверхности Земли) точки массы т из положения в положение (рис. 244).

Решение:

Поэтому за потенциал поля силы тяжести можно принять

Отсюда работа силы тяжести, независимо от пути 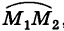, равна

Замечание. Аналогичные результаты справедливы для криволинейного интеграла, взятого по пространственной кривой. В частности, если

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник