На чем основано измерение отрезков
Математика. 5 класс
Конспект урока
Перечень рассматриваемых вопросов:
– понятие длины отрезка;
– равные отрезки на чертежах;
– определение длины отрезков.
Длина отрезка – число, которое показывает, сколько раз в отрезке содержится единичный отрезок.
Единичный отрезок – это отрезок, длина которого принята за единицу измерения.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. –М.: Просвещение, 2009. – 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95с.
Теоретический материал для самостоятельного изучения
Каждому человеку неоднократно приходилось что-то измерять: свой рост, длину прыжка, высоту потолка и многое другое. Все эти действия означают вычисление величины какого-нибудь отрезка. Каким же образом можно измерить длину отрезка? На этот вопрос ответим в ходе урока.
За свою историю человечество придумало много разных единиц длины. Позже появились меры, заимствованные из природы:
– пядь – расстояние между растянутыми большим и указательным пальцами;
– вершок – длина основной фаланги указательного пальца;
– локоть – расстояние от локтевого сустава до конца вытянутого среднего пальца руки.
Некоторые названия сохранились до сих пор: ярд, фут, пядь, дюйм.
Ну, а герои одного известного мультфильма измеряли длину удава в попугаях. В зависимости от того, в ком измеряли удава, он становился то длиннее, то короче.
Два слонёнка, пять мартышек или тридцать восемь попугаев.
«А в попугаях я гораздо длиннее!» – воскликнул удав.
На самом деле мы с вами понимаем, что его размеры не менялись. Тогда возникает вопрос: в чём измерять? Что брать за единицу длины? Слонёнка, попугая или мартышку.
Измерить длину какого-нибудь отрезка в заданных единицах измерения – значит найти число, показывающее, сколько единичных отрезков поместится в данном отрезке.
Длиной отрезка называют число, которое показывает, сколько раз в отрезке содержится единица измерения.
Отрезок, длина которого принята за единицу измерения, называется единичным отрезком.
Чем же можно измерить длину отрезка?
Наиболее древними геометрическими инструментами являются линейка и циркуль, последний был изобретён в первом веке в Древней Греции.
Для более точных измерений используют миллиметровую линейку и штангенциркуль.
Далее построим отрезок ВК заданной длины –например, 8см. Для этого отметим точку В и приложим к ней линейку, совместив точку В с нулём. Затем отмеряем с помощью линейки 8 см, отмечаем точку К и соединяем обе точки линией.
Такой отрезок можно построить и с помощью циркуля. Для этого отметим точку В. Приложим к линейке циркуль, выставив его ножки на восемь сантиметров. Перенесём циркуль к точке В, поместив на неё одну ножку, а другой ножкой поставим точку К. Соединив обе точки линией, получим отрезок с длиной 8 см.
Отрезки можно сравнить с помощью измерителя –например, циркуля. Для этого попеременно подставляем ножки циркуля ко всем предложенным для сравнения отрезкам. При этом они должны быть выставлены по одному из отрезков. Если длины отрезков одинаковы, то отрезки считают равными и пишут CD = КМ.
Если один из отрезков является частью другого, следовательно, он короче. Например, ЕН короче EF, так как отрезок EH является частью EF.
Рассмотрим ещё одно свойство длин.
Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ. Пишут: АВ = АС + СВ.
Наши органы чувств – это один из способов получения информации об окружающем нас мире, но информация полученная таким образом, бывает искажена.
Посмотрите на рисунки и ответьте на вопрос, равны ли отрезки?
На первый взгляд покажется, что правый отрезок больше, чем левый, но при сравнении с помощью линейки окажется, что отрезки равны.
Такая же ситуация, складывается и со следующей картинкой. Кажется, что нижний отрезок больше, чем верхний, но при наложении линейки окажется, что отрезки равны.
В другом же случае на тот же вопрос о равенстве отрезков ответ очевиден.
Таким образом, можно сделать вывод, что глазомерные оценки геометрических реальных величин неточны.
Разбор решения заданий тренировочного модуля
№1. Тип задания: выбор элемента из выпадающего списка.
Сравните длины горизонтального и вертикального отрезков?
Правильный ответ: при выполнении данного задания нужно использовать линейку, нужно измерить длину каждого отрезка и сравнить их. В результате измерений мы увидим, что отрезки равны.
№2. Тип задания: выделение цветом.
Точка К расположена на прямой между точками А и В. Длина отрезка АК = 8 см, длина отрезка КВ на 2 см больше длины отрезка АК. Какова длина отрезка АВ?
Выберите правильный ответ: 6 см; 10 см; 12 см; 18 см.
Решение: изобразим условие задачи на рисунке.
Измерение отрезков
Цели урока:
2) Развивающая: развитие умений применять полученные теоретические знания на практике, развитие внимания, аналитических способностей.
3) Воспитывающая: воспитание интереса к изучению математики, ответственности, самостоятельности.
Литература: «Геометрия 7 — 9 класс» Л. С. Атанасян и др.
План урока:
1. Организационный момент.
2. Актуализация опорных знаний.
3. Получение знаний.
4. Закрепление нового материала.
6. Домашнее задание.
Ход урока:
1. Организационный момент.
Приветствие учащихся. Ставятся цели и определяются задачи урока.
Объявляется тема урока. Учащиеся записывают тему урока и дату в рабочих тетрадях.
2. Актуализация опорных знаний.
На прошлом уроке мы говорили о сравнении двух отрезков способом наложения их друг на друга.
– Скажите, в каком случае два отрезка называют равными? (если их можно совместить наложением)
Сегодня на уроке мы снова поговорим об измерении отрезков, а точнее научимся измерять отрезки и выражать их длину в миллиметрах, сантиметрах, метрах.
Для начала, давайте, ответим на несколько вопросов.
– Что называют серединой отрезка?
– Что называют биссектрисой угла?
3. Получение знаний.
В повседневной жизни нам часто приходится сталкиваться с измерением высот зданий, сооружений, а также с измерением расстояний, которые мы прошли или проехали. С точки зрения геометрии мы имеем в таких случаях дело с измерением отрезков.
Измерение отрезков основано на сравнении их с некоторым отрезком, принятым за единицу измерения. Такой отрезок также называют масштабным отрезком.
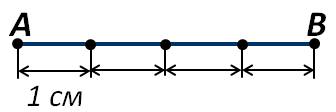
Давайте определим длину некоторого отрезка АВ, приняв за единицу измерения сантиметр (рисунок 1). Видим, что в данном отрезке АВ сантиметр укладывается ровно четыре раза, а это означает, что его длина равна четыре сантиметра. Обычно говорят кратко: «Отрезок АВ равен четыре сантиметра». А записывают так: АВ = 4 см.
Рисунок 1.
Но может оказаться так, что отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке.
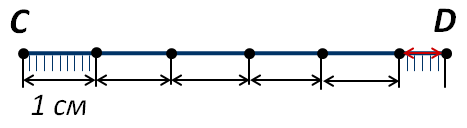
Возьмём отрезок CD (рисунок 2). Сантиметр укладывается в отрезок пять раз, но при этом получается остаток. В таком случае единицу измерения необходимо разделить на равные части, обычно делят на десять равных частей, и определить, сколько таких частей укладывается в остатке. В нашем случае в остатке шесть раз укладывается десятая часть отрезка, поэтому длина отрезка CD равна пять целых шесть десятых сантиметра. Отметим, что одну десятую часть сантиметра называют миллиметром (мм).
Рисунок 2.
Однако может возникнуть ситуация, когда и миллиметр не будет укладываться в остатке целое число раз, и получится новый остаток. Тогда и миллиметр можно разделить на 10 частей и продолжить процесс измерения.
Единицей измерения отрезка может быть не только сантиметр, но и другой отрезок.
Выбрав единицу измерения, можно измерить любой отрезок, выразить его длину некоторым положительным числом.
Исходя из проделанного выше, можно сказать, что это число показывает, сколько раз единица измерения и её части укладываются в измеряемом отрезке.
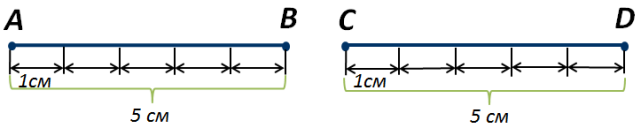
Возьмём два равных отрезка АВ и СD (рисунок 3). Единицы измерения в этих отрезках укладываются одинаковое число раз, равные отрезки имеют равные длины.
Рисунок 3.
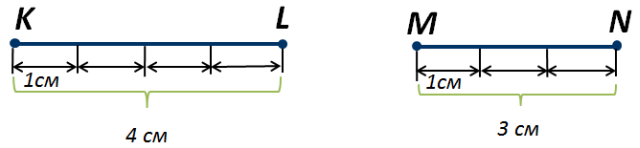
Если же мы возьмём два неравных отрезка KL и MN (рисунок 4), то увидим, что в меньшем отрезке MN единица измерения укладывается меньшее число раз, чем в отрезке KL, меньший отрезок имеет меньшую длину.
Рисунок 4.
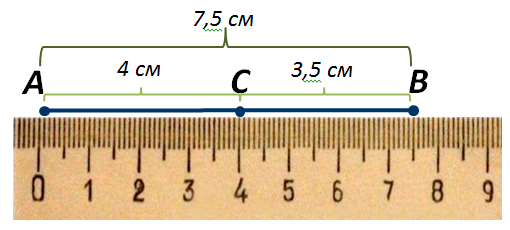
Теперь рассмотрим отрезок АВ (рисунок 5). Точка С делит его на два отрезка: АС и СВ. Измерим эти отрезки. Видим, что отрезок АС равен четыре сантиметра, отрезок СВ равен три целых пять десятых сантиметра и отрезок АВ равен семь целых пять десятых сантиметра. Получили:
Таким образом, сформулируем следующее.
Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Рисунок 5.
Следует сказать, что если длина некоторого отрезка АВ в k раз больше отрезка CD, то записывают это следующим образом: АВ=kCD.
Отметим также, что длина отрезка называется расстоянием между концами этого отрезка.
Поговорим о единицах измерения. Для измерения отрезков и нахождения расстояний используются различные единицы измерения. Стандартной международной единицей измерения отрезков является метр — отрезок, который приблизительно равен 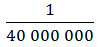
В одном метре сто сантиметров (1 м =100 см), а один сантиметр содержит десять миллиметров (1 см = 10 мм).
При измерении небольших расстояний, например, расстояния между точками на листе бумаги или нахождении длины карандаша за единицу измерения принимают сантиметр или миллиметр. Высоту дерева можно измерить в метрах. А вот расстояние, которое мы пройдём на лыжах, можно измерить в километрах.
Можно также использовать и такие единицы измерения, как дециметр (1 дм = 10 см), морская миля, равная одной целой восьмистам пятидесяти двум тысячным километра (1 миля = 1,852 км). А вот для измерения очень больших расстояний в астрономии используется такая единица измерения, как световой год (это путь, который проходит свет в течение одного года).
Для измерения расстояний могут использоваться различные инструменты. Например, в техническом черчении используется масштабная миллиметровая линейка. Для измерения расстояний на местности пользуются рулеткой. А вот для измерения диаметра трубки можно воспользоваться штангенциркулем.
4. Закрепление нового материала.
Для закрепления материала учащимся предлагается выполнить следующие практические задания.
Задание 1. На прямой отмечены точки А, В и С. Отрезок АВ = 50 мм, а отрезок АС = 1,7 дм. Найдите длину отрезка ВС в сантиметрах. Рассмотрите различные варианты взаимного расположения точек.
Решение: Переведём значения длин отрезков в сантиметры.
АВ = 50 мм = 5 см; АС=1,7 дм =17 см.
Рисунок 6.
ВС = АС — АВ, ВС = 17 см — 5 см = 12 см.
Рисунок 7.
ВС = АВ + АС, ВС = 5 см + 17 см = 22 см.
Рисунок 8.
В данном случае задача не имеет решения, так как АС > АВ.
Ответ: 12 см или 22 см.
Задание 2. На прямой MN лежит точка L. Найдите длину отрезка MN, если ML = 7 см, а LN = 4ML.
Решение: MN = ML + LN = ML + 4ML = 5ML;
Рисунок 9.
Ответ: 35 см.
Задание 3. Точка О — середина отрезка KL, длина которого равна 8,4 см. От точки О на прямой KL отложены отрезки ОМ = 2 см и ON = 5 см. Найдите длины отрезков КМ и KN, если MN = 3 см.
Рисунок 10.
Решение: Так как О — середина отрезка KL, то KO = ОL = 4,2 см.
KM = KO + OM = 4,2 + 2 =6,2 см.
Из последнего выражения видим, чтобы найти длину отрезка KN, нам необходимо найти длину отрезка LN.
Так как ОL = 4,2 см и ON = 5 см, то LN = ON — ОL = 5 — 4,2 = 0,8 см.
Тогда KN = 8,4 + 0,8 = 9,2 см.
Ответ: 6,2 см; 9,2 см.
5. Рефлексия.
Подводятся итоги урока, обсуждается, что учащиеся узнали. Учащиеся задают вопросы, возникшие при изучении нового материала и выполнении практических заданий. Затем ребята по кругу высказываются одним предложением, выбирая начало фразы записанной на доске:
4. я выполнял задания…
7. у меня получилось …
Оценивается работа учащихся на уроке.
6. Домашнее задание: § 4, № 26, 34.
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Середина отрезка – это точка, делящая его пополам, т.е. на два равных отрезка.
Две фигуры, имеющие одинаковую форму и одинаковые размеры, называют равными.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Длина отрезка – это расстояние между концами этого отрезка.
1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Теоретический материал для самостоятельного изучения.
«Измерь самого себя – и ты станешь настоящим геометром!» – однажды сказал средневековый философ Марсилио Фичино.
И в этом есть доля правды, ведь измерения – это одно из важных действий в геометрии.
Поэтому сегодня мы будем измерять данный отрезок с помощью линейки и выражать результат в выбранной единице измерения.
В жизни часто приходится измерять длины, будь то длина дороги или ширина комнаты. В геометрии мы будем измерять отрезки. На чём же основано измерение отрезков?
Основа любого измерения – это сравнение величин с другими, принятыми за единицу измерения этой величины.
То же самое и с измерением длины отрезка. Т.е. измерение отрезка – это сравнение длины отрезка с некоторым другим отрезком (масштабным), выбранным за единицу измерения.
Если взять за единицу измерения сантиметр, то, определяя длину отрезка, мы узнаём, сколько раз в заданном отрезке укладывается сантиметр.
Например, один сантиметр укладывается в отрезке АВ семь раз, следовательно, длина отрезкасемь сантиметров.
Если масштабный отрезок не укладывается целое число раз в измеряемом отрезке, то единицу измерения делят ещё на части, обычно на десять. Далее, определяют, сколько такая часть укладывается в остатке.
Например, в отрезке АВ один сантиметр укладываетсятри раза, в остатке ровно 7 раз укладывается десятая часть сантиметра, а десятая часть сантиметра это миллиметр, т.е. длина отрезка АВ три сантиметра семь миллиметров или три целых семь десятых сантиметра.
Но бывает, что и при меньшем масштабном отрезке есть остаток, тогда говорят, что длина отрезка приближенно равна определенному значению.
Для более точного измерения этого отрезка указанную часть единицы измерения (в данном случае миллиметр) можно разделить на 10 равных частей и продолжить процесс измерения, но обычно так не делают, оставляют приближенное значение длины отрезка.
Стоит отметить, что за единицу измерения можно принимать не только сантиметр, но и любой другой отрезок. Например, метр, милю. А выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.
Два отрезка считаются равными, если единица измерения и её части укладываются в этих отрезках одинаковое число раз, т.е. равные отрезки имеют равные длины.
Если один отрезок меньше другого, то единица измерения (или её часть) укладываются в этом отрезке меньшее число раз, чем в другом, т.е. меньший отрезок имеет меньшую длину.
AD= 4 см + 1,2 см + 1,3 см = 6 см.
Таким образом, длина отрезка – это расстояние между концами этого отрезка.
Для измерения длины отрезкаиспользуют различные приборы: линейка, штангенциркуль, рулетка.
Итак, сегодня вы получили представлениео том, как измерять данный отрезок с помощью линейки и выражать результат в выбранной единице измерения.
Возьмём несколько отрезков и соединим их между собой друг за другом под углом, не равным 180 градусам, полученная фигура называется ломаной. Она может выглядеть так.
Если начало и конец ломанной совпадут, то она считается замкнутой ломаной.
При этом у ломаной можно определить длину, т.к. она состоит из отрезков, длину которых можно измерить. Поэтому длина ломанойравна сумме длин отрезков, из которых она состоит.
При этом,длина незамкнутой ломаной не меньше длины отрезка, соединяющего ее концы.
1. Какова длина отрезка АВ, если точка О делит отрезок АВ на две части, при этом АО = 5см, ОВ = 2,3 см?
По условию задачи, точка О делит отрезок АВ на две части, следовательно, длина отрезка АВ = АО + ОВ = 5см + 2,3 см =7,3 см.
2. На прямой а отмечены точки А, С, E, причём АС = 5 см, СE = 7 см. Чему может быть равна длина отрезка АE?
Для решения задачи нужно нарисовать рисунок в соответствии с условием. Тогда:
АЕ = АС + СЕ = 5см + 7см = 12 см.
А если точки поменять местами, АЕ = СЕ – СА = 7см – 5см = 2см. Других вариантов быть не может, поэтому получается два ответа.
§ 4. Измерение отрезков
Длина отрезка
На рисунке 27 в отрезке АВ сантиметр укладывается ровно два раза. Это означает, что длина отрезка АВ равна 2 см. Обычно говорят кратко: «Отрезок АВ равен 2 см» — и пишут: АВ = 2 см.
Может оказаться так, что отрезок, принятый за единицу измерения, не укладывается целое число раз в измеряемом отрезке — получается остаток. Тогда единицу измерения делят на равные части, обычно на 10 равных частей, и определяют, сколько раз одна такая часть укладывается в остатке. Например, на рисунке 27 в отрезке АС сантиметр укладывается 3 раза, и в остатке ровно 4 раза укладывается одна десятая часть сантиметра (миллиметр), поэтому длина отрезка АС равна 3,4 см.
Возможно, однако, что и взятая часть единицы измерения (в данном случае миллиметр) не укладывается в остатке целое число раз, и получается новый остаток. Так будет, например, с отрезком AD на рисунке 27, в котором сантиметр укладывается три раза с остатком, а в остатке миллиметр укладывается восемь раз вновь с остатком. В таком случае говорят, что длина отрезка AD приближённо равна 3,8 см.
Для более точного измерения этого отрезка указанную часть единицы измерения (миллиметр) можно разделить на 10 равных частей и продолжить процесс измерения. Мысленно этот процесс можно продолжать и дальше, измеряя длину отрезка со всё большей точностью. На практике, однако, пользуются приближёнными значениями длин отрезков.
За единицу измерения можно принимать не только сантиметр, но и любой другой отрезок. Выбрав единицу измерения, можно измерить любой отрезок, т. е. выразить его длину некоторым положительным числом. Это число показывает, сколько раз единица измерения и её части укладываются в измеряемом отрезке.
Если два отрезка равны, то единица измерения и её части укладываются в этих отрезках одинаковое число раз, т. е. равные отрезки имеют равные длины. Если же один отрезок меньше другого, то единица измерения (или её часть) укладывается в этом отрезке меньшее число раз, чем в другом, т. е. меньший отрезок имеет меньшую длину.
На рисунке 28 изображён отрезок АВ. Точка С делит его на два отрезка: АС и СВ. Мы видим, что АС = 3см, СВ = 2,7 см, АВ = 5,7 см.
Таким образом, АС + СВ = АВ. Ясно, что и во всех других случаях, когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Если длина отрезка CD в k раз больше длины отрезка АВ, то пишут CD = kAB.
Длина отрезка называется также расстоянием между концами этого отрезка.
Единицы измерения. Измерительные инструменты
Для измерения отрезков и нахождения расстояний на практике используют различные единицы измерения. Стандартной международной единицей измерения отрезков выбран метр — отрезок, приближённо равный 1/40 000 000 части земного меридиана. Эталон метра в виде специального металлического бруска хранится в Международном бюро мер и весов во Франции. Копии эталона хранятся в других странах, в том числе и в России. Один метр содержит сто сантиметров. В одном сантиметре десять миллиметров.
При измерении небольших расстояний, например расстояния между точками, изображёнными на листе бумаги, за единицу измерения принимают сантиметр или миллиметр. Расстояние между отдельными предметами в комнате измеряют в метрах, расстояние между населёнными пунктами — в километрах. Используются и другие единицы измерения, например дециметр, морская миля (1 миля равна 1,852 км). В астрономии для измерения очень больших расстояний за единицу измерения принимают световой год, т. е. путь, который свет проходит в течение одного года.
Мы назвали единицы измерения расстояний, которые используются на практике в наше время. В старину в разных странах существовали свои единицы измерения. Так, на Руси использовались аршин (0,7112 м), сажень (2,1336 м) и др.
На практике для измерения расстояний пользуются различными инструментами. Например, в техническом черчении употребляется масштабная миллиметровая линейка. Для измерения диаметра трубки используют штангенциркуль (рис. 29). С его помощью можно измерять расстояния с точностью до 0,1 мм. Для измерения расстояний на местности пользуются рулеткой, которая представляет собой ленту с нанесёнными на ней делениями (рис. 30).
Практические задания
24. Измерьте ширину и длину учебника геометрии и выразите их в сантиметрах и в миллиметрах.
25. Измерив толщи: у учебника геометрии без обложки, найдите толщину одного листа.
26. Найдите длины всех отрезков, изображённых на рисунке 31, если за единицу измерения принят отрезок: a) KL; б) АВ.
27. Начертите отрезок АВ и луч h. Пользуясь масштабной линейкой, отложите на луче h от его начала отрезки, длины которых равны
28. Начертите прямую и отметьте на ней точки А и В. С помощью масштабной линейки отметьте точки С и D так, чтобы точка В была серединой отрезка АС, а точка D — серединой отрезка ВС.
29. Начертите прямую АВ. С помощью масштабной линейки отметьте на этой прямой точку С, такую, что АС = 2 см. Сколько таких точек можно отметить на прямой АВ?
Ответ
Задачи к § 4
30. Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.
31. Точка В делит отрезок АС на два отрезка. Найдите длину отрезка ВС, если:
а) АВ = 3,7 см, АС = 7,2 см;
б) АВ = 4 мм, АС = 4 см.
32. Точки А, Б и С лежат на одной прямой. Известно, что АВ = 12 см, ВС = 13,5 см. Какой может быть длина отрезка АС?
33. Точки В, D и М лежат на одной прямой. Известно, что BD= 7 см, MD= 16 см. Каким может быть расстояние ВМ?
34. Точка С — середина отрезка АВ, равного 64 см. На луче СА отмечена точка D так, что СD = 15см. Найдите длины отрезков BD и DA.
35. Расстояние между Москвой и С.-Петербургом равно 650 км. Город Тверь находится между Москвой и С.-Петербургом в 170 км от Москвы. Найдите расстояние между Тверью и С.-Петербургом, считая, что все три города расположены на одной прямой.
36. Лежат ли точки А, Б и С на одной прямой, если АС = 5 см, АВ = 3 см, ВС = 4 см?
Если точки А, В и С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (АВ + ВС) равна 7 см. Поэтому точки А, В и С не лежат на одной прямой.
37. Точка С — середина отрезка АВ, точка О — середина отрезка АС. Найдите:
а) АС, СВ, АО и ОВ, если АВ = 2 см;
б) АВ, АС, АО и ОВ, если СВ = 3,2 м.
38. На прямой отмечены точки О, А и В так, что ОА = 12 см, ОВ = 9 см. Найдите расстояние между серединами отрезков О А и ОВ, если точка О:
а) лежит на отрезке АВ;
б) не лежит на отрезке АВ.
39. Отрезок, длина которого равна а, разделён произвольной точкой на два отрезка. Найдите расстояние между серединами этих отрезков.
40. Отрезок, равный 28 см, разделён на три неравных отрезка. Расстояние между серединами крайних отрезков 16 см. Найдите длину среднего отрезка.
Ответы к задачам
31. а) 3,5 см; б) 36 мм.
32. 25,5 см или 1,5 см.
34. BD = 47 см, DA = 17 см.
37. а) АС = 1см, СВ = 1см, АО = 0,5см, ОВ=1,5см; б) АВ = 6,4м, АС = 3,2м, АО = 1,6 м, ОВ = 4,8м.