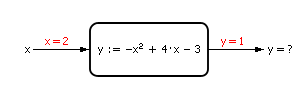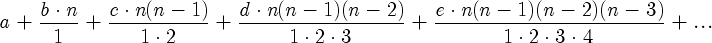На чем основано моделирование
Моделирование данных: зачем нужно и как реализовать
Моделирование данных ощутимо упрощает взаимодействие между разработчиками, аналитиками и маркетологами, как и сам процесс создания отчетов. Поэтому я перевела статью IBM Cloud Education о ценности моделирования и от себя добавила инфо о способах трансформации данных для моделирования.
Моделирование данных
Узнайте, как моделирование данных использует абстракцию для представления и лучшего понимания природы данных в информационной системе предприятия.
Что такое моделирование данных
Моделирование данных — это создание визуального представления о всей информационной системе либо ее части. Цель в том, чтобы проиллюстрировать типы данных, которые используются и хранятся в системе, отношения между этими типами данных, способы группировки и организации данных, их форматы и атрибуты.
Модели данных строятся на основе бизнес-потребностей. Правила и требования к модели данных определяются заранее на основе обратной связи с бизнесом, поэтому их можно включить в разработку новой системы или адаптировать к существующей.
Данные можно моделировать на различных уровнях абстракции. Процесс начинается со сбора бизнес-требований от заинтересованных сторон и конечных пользователей. Эти бизнес-правила затем преобразуются в структуры данных. Модель данных можно сравнить с дорожной картой, планом архитектора или любой формальной схемой, которая способствует более глубокому пониманию того, что разрабатывается.
Моделирование данных использует стандартизированные схемы и формальные методы. Это обеспечивает последовательный и предсказуемый способ управления данными в организации или за ее пределами.
В идеале модели данных — это живые документы, которые развиваются вместе с потребностями бизнеса. Они играют важную роль в поддержке бизнес-процессов и планировании ИТ-архитектуры и стратегии. Моделями данных можно делиться с поставщиками, партнерами и коллегами.
Преимущества моделирования данных
Моделирование упрощает просмотр и понимание взаимосвязей между данными для разработчиков, архитекторов данных, бизнес-аналитиков и других заинтересованных лиц. Кроме того, моделирование данных помогает:
Уменьшить количество ошибок при разработке программного обеспечения и баз данных.
Унифицировать документацию на предприятии.
Повысить производительность приложений и баз данных.
Упростить отображение данных по всей организации.
Улучшить взаимодействие между разработчиками и командами бизнес-аналитики.
Упростить и ускорить процесс проектирования базы данных на концептуальном, логическом и физическом уровнях.
Типы моделей данных
Разработка баз данных и информационных систем начинается с высокого уровня абстракции и с каждым шагом становится все точнее и конкретнее. В зависимости от степени абстракции модели данных можно разделить на три категории. Процесс начинается с концептуальной модели, переходит к логической модели и завершается физической моделью.
Концептуальные модели данных. Также они называются моделями предметной области и описывают общую картину: что будет содержать система, как она будет организована и какие бизнес-правила будут задействованы. Концептуальные модели обычно создаются в процессе сбора исходных требований к проекту. Как правило, они включают классы сущностей (вещи, которые бизнесу важно представить в модели данных), их характеристики и ограничения, отношения между сущностями, требования к безопасности и целостности данных. Любые обозначения обычно просты.
Логические модели данных уже не так абстрактны и предоставляют более подробную информацию о концепциях и взаимосвязях в рассматриваемой области. Они содержат атрибуты данных и показывают отношения между сущностями. Логические модели данных не определяют никаких технических требований к системе. Этот этап часто пропускается в agile или DevOps-практиках. Логические модели данных могут быть полезны для проектов, ориентированных на данные по своей природе. Например, для проектирования хранилища данных или разработки системы отчетности.
Физические модели данных представляют схему того, как данные будут храниться в базе. По сути, это наименее абстрактные из всех моделей. Они предлагают окончательный дизайн, который может быть реализован как реляционная база данных, включающая ассоциативные таблицы, которые иллюстрируют отношения между сущностями, а также первичные и внешние ключи для связи данных.
Процесс моделирования данных
Моделирование данных начинается с договоренности о том, какие символы используются для представления данных, как размещаются модели и как передаются бизнес-требования. Это формализованный рабочий процесс, включающий ряд задач, которые должны выполняться итеративно. Сам процесс обычно выглядят так:
Определите сущности. На этом этапе идентифицируем объекты, события или концепции, представленные в наборе данных, который необходимо смоделировать. Каждая сущность должна быть целостной и логически отделенной от всех остальных.
Определите ключевые свойства каждой сущности. Каждый тип сущности можно отличить от всех остальных, поскольку он имеет одно или несколько уникальных свойств, называемых атрибутами. Например, сущность «клиент» может обладать такими атрибутами, как имя, фамилия, номер телефона и т.д. Сущность «адрес» может включать название и номер улицы, город, страну и почтовый индекс.
Определите связи между сущностями. Самый ранний черновик модели данных будет определять характер отношений, которые каждая сущность имеет с другими. В приведенном выше примере каждый клиент «живет по» адресу. Если бы эта модель была расширена за счет включения сущности «заказы», каждый заказ также был бы отправлен на адрес. Эти отношения обычно документируются с помощью унифицированного языка моделирования (UML).
Полностью сопоставьте атрибуты с сущностями. Это гарантирует, что модель отражает то, как бизнес будет использовать данные. Широко используются несколько формальных шаблонов (паттернов) моделирования данных. Объектно-ориентированные разработчики часто применяют шаблоны для анализа или шаблоны проектирования, в то время как заинтересованные стороны из других областей бизнеса могут обратиться к другим паттернам.
Назначьте ключи по мере необходимости и определите степень нормализации. Нормализация — это метод организации моделей данных, в которых числовые идентификаторы (ключи) назначаются группам данных для установления связей между ними без повторения данных. Например, если каждому клиенту назначен ключ, этот ключ можно связать как с его адресом, так и с историей заказов, без необходимости повторять эту информацию в таблице с именами клиентов. Нормализация помогает уменьшить объем дискового пространства, необходимого для базы данных, но может сказываться на производительности запросов.
Завершите и проверьте модель данных. Моделирование данных — это итеративный процесс, который следует повторять и совершенствовать под потребности бизнеса.
Типы моделирования данных
Моделирование данных развивалось вместе с системами управления базами данных (СУБД), при этом типы моделей усложнялись по мере роста потребностей предприятий в хранении данных.
Иерархические модели данных представляют отношения «один ко многим» в древовидном формате. В модели этого типа каждая запись имеет единственный корень или родительский элемент, который сопоставляется с одной или несколькими дочерними таблицами. Эта модель была реализована в IBM Information Management System (IMS) в 1966 году и быстро нашла широкое применение, особенно в банковской сфере. Хотя этот подход менее эффективен, чем недавно разработанные модели баз данных, он все еще используется в системах расширяемого языка разметки (XML) и географических информационных системах (ГИС).
Реляционные модели данных были предложены исследователем IBM Э. Ф. Коддом в 1970 году. Они до сих пор встречаются во многих реляционных базах данных, обычно используемых в корпоративных вычислениях. Реляционное моделирование не требует детального понимания физических свойств используемого хранилища данных. В нем сегменты данных объединяются с помощью таблиц, что упрощает базу данных.
Реляционные базы данных часто используют язык структурированных запросов (SQL) для управления данными. Эти базы подходят для поддержания целостности данных и минимизации избыточности. Они часто используются в кассовых системах, а также для других типов обработки транзакций.
В ER-моделях данных используют диаграммы для представления взаимосвязей между сущностями в базе данных. ER-модель представляет собой формальную конструкцию, которая не предписывает никаких графических средств её визуализации. В качестве стандартной графической нотации, с помощью которой можно визуализировать ER-модель, была предложена диаграмма «сущность-связь» (Entity-Relationship diagram). Однако для визуализации ER-моделей могут использоваться и другие графические нотации, либо визуализация может вообще не применяться (например, только текстовое описание).
Объектно-ориентированные модели данных получили распространение как объектно-ориентированное программирование и стали популярными в середине 1990-х годов. Вовлеченные «объекты» — это абстракции сущностей реального мира. Объекты сгруппированы в иерархии классов и имеют связанные черты. Объектно-ориентированные базы данных могут включать таблицы, но могут также поддерживать более сложные связи. Этот подход часто используется в мультимедийных и гипертекстовых базах данных.
Размерные модели данных разработал Ральф Кимбалл для быстрого поиска данных в хранилище. Реляционные и ER-модели делают упор на эффективное хранение и уменьшают избыточность данных, а размерные модели упорядочивает данные таким образом, чтобы легче было извлекать информацию и создавать отчеты. Это моделирование обычно используется в системах OLAP.
Две популярные размерные модели данных — это схемы «звезда» и «снежинка». В схеме «звезда» данные организованы в факты (измеримые элементы) и измерения (справочная информация), где каждый факт окружен связанными с ним измерениями в виде звездочки. Схема «снежинка» напоминает схему «звезда», но включает дополнительные слои связанных измерений, что усложняет схему ветвления.
Инструменты для моделирования данных
Сегодня широко используются многочисленные коммерческие и CASE-решения с открытым исходным кодом, в том числе различные инструменты моделирования данных, построения диаграмм и визуализации. Вот несколько примеров:
erwin Data Modeler — это инструмент моделирования данных, основанный на языке IDEF1X, который теперь поддерживает и другие нотации, включая нотацию для размерного моделирования.
Enterprise Architect — это инструмент визуального моделирования и проектирования, который поддерживает моделирование корпоративных информационных систем и архитектур, программных приложений и баз данных. Он основан на объектно-ориентированных языках и стандартах.
ER/Studio — это программа для проектирования баз данных, совместимая с некоторыми из самых популярных СУБД. Она поддерживает как реляционное, так и размерное моделирование данных.
Бесплатные инструменты моделирования данных включают решения с открытым исходным кодом, такие как Open ModelSphere.
Для того, чтобы преобразовать данные в структуру, которая соответствует требованиям модели, можно использовать встроенный механизм регулярных запросов, которые выполняются в Google BigQuery, Scheduled Queries и AppScript. Их легко можно освоить, потому что это привычный SQL, но проводить отладку в Scheduled Queries практически нереально. Особенно, если это какой-то сложный запрос или каскад запросов.
Есть специализированные инструменты для управления SQL-запросами, например, dbt и Dataform.
dbt (data build tool) — это фреймворк с открытым исходным кодом для выполнения, тестирования и документирования SQL-запросов, который позволяет привнести элемент программной инженерии в процесс анализа данных. Он помогает оптимизировать работу с SQL-запросами: использовать макросы и шаблоны JINJA, чтобы не повторять в сотый раз одни и те же фрагменты кода.
Главная проблема, которую решают специализированные инструменты — это уменьшение времени, необходимого на поддержку и обновление. Это достигается за счет удобства отладки.
Моделирование
Моделирование — это метод воспроизведения и исследования определённого фрагмента действительности (предмета, явления, процесса, ситуации) или управления им, основанный на представлении объекта с помощью его копии или подобия — модели (см. Модель). Модель обычно представляет собой либо материальную копию оригинала, либо некоторый условный образ, представленный в абстрактной (мысленной или знаковой) форме и содержащий существенные свойства моделируемого объекта. Процедуры создания моделей широко используются как в научно-теоретических, так и в прикладных сферах человеческой деятельности.
В научном познании (см. Наука) модель рассматривается как «объект-подобие» или «объект-заместитель» объекта-оригинала, воспроизводящий определённые его характеристики. В этом смысле модель всегда соответствует объекту-оригиналу — в тех свойствах, которые подлежат изучению, но в то же время отличается от него по ряду других признаков, что делает модель удобной для исследования изучаемого объекта. Результаты разработки и исследования моделей при определённых условиях, принимаемых в методологии науки и специфических для различных областей и типов моделей, распространяются на оригинал. Использование метода моделирования в научном познании диктуется необходимостью раскрыть такие стороны объектов, которые либо невозможно постигнуть путём непосредственного изучения, либо непродуктивно изучать их таким образом в силу каких-либо ограничений.
В научном познании возможны два способа моделирования:
Модели, применяемые в научном познании, разделяются на два больших класса:
Соответственно указанным различениям выделяют основные разновидности моделирования. Каждое из них применяется в зависимости от особенностей изучаемого объекта и характера познавательных задач.
Предметно-физическое моделирование широко используется как в научной практике, так и в сфере материального производства. Такое моделирование всегда предполагает, что модель должна быть сходна с оригиналом по физической природе и отличаться от него лишь численными значениями ряда параметров. Наряду с этим в практике научного исследования часто используется и такой вид моделирования, при котором модель строится из объектов иной физической природы, чем оригинал, но описывается одинаковой с ним системой математических зависимостей. В отличие от предметно-физического этот вид моделирования называют предметно-математическим. Предметная модель становится здесь объектом испытания и изучения, в результате которого создаётся её математическое описание. Последнее затем переносится на моделируемый объект, характеризуя его структуру и функционирование.
В развитой науке, особенно при переходе к теоретическим исследованиям, широко используется моделирование с применением идеальных моделей. Этот способ получения знаний об объектах может быть охарактеризован как моделирование посредством идеализированных представлений. Он является ведущим инструментом теоретического исследования. Активно используя модельные представления, научное исследование вместе с тем применяет и так называемое знаковое моделирование, которое основано на построении и испытании математических моделей некоторого класса явлений, без использования при этом вспомогательного физического объекта, который подвергается испытанию. Последнее отличает знаковую модель от предметно-математической. Такой вид моделирования иногда называют также абстрактно-математическим. Он требует построения знаковой модели, представляющей некоторый объект, где отношения и свойства объекта представлены в виде знаков и их связей. Эта модель затем исследуется чисто логическими средствами, и новое знание возникает в результате дедуктивного развёртывания модели без обращения к предметной области, на основании которой выросла данная знаковая модель. В абстрактно-математическом моделировании модель — это конструкция, изоморфная моделируемой системе. При таком моделировании каждому объекту системы ставится в соответствие определённый элемент моделирующей конструкции, а свойствам и отношениям объектов соответствуют свойства и отношения элементов.
Классическими примерами моделей, основанных на изоморфизме, являются модели аксиоматических систем в математике. Они задают семантику формальных построений и создают возможность для содержательной интерпретации аксиом. Сами аксиомы, как и следствия из них, считаются предложениями некоторого формального языка. Кроме того, задана область интерпретаций, представляющая собой множество индивидных объектов. Изоморфизм задаётся функцией, сопоставляющей каждому имени языка некоторый объект из заданного множества, а каждому выражению языка некоторое отношение объектов этого же множества. Если любое высказывание, которое выведено из аксиом, истинно в области интерпретаций (то есть соответствует реальным отношениям объектов), то эта область называется моделью системы аксиом. Моделирование в математике используется, например, для доказательства непротиворечивости формальных систем.
Этот вид моделирования используется не только в чистой математике, но также при математическом описании природных, общественных, технологических и других сложных систем. Смысл такого описания состоит в том, что отношения между элементами системы выражаются с помощью уравнений, причём так, чтобы каждому термину содержательного описания системы соответствовала какая-либо величина (константа или переменная) или функция, фигурирующая в уравнении. Сами уравнения называются при этом моделью. Как правило, абстрактно-математическое моделирование требует абстракции (см. Абстракция), то есть отвлечения от некоторых свойств и отношений в моделируемой системе. Это позволяет достичь общности модели и утверждать, что она, игнорируя частности, описывает достаточно широкий круг процессов или систем. К тому же без таких упрощений моделирование оказывается бессмысленным ( чрезмерной сложности модели) или вообще невозможным. Другим важным гносеологическим условием моделирования является измеримость всех описываемых объектов и отношений. Чтобы построить модель, необходимо найти их числовое представление. Всякий моделируемый процесс должен быть полностью охарактеризован с помощью параметров, поддающихся измерению.
Другая разновидность моделирования с применением идеальных моделей основана на понятии «чёрный ящик». Этим термином принято называть объект, внутренняя структура которого недоступна для наблюдения и о котором можно судить только по его внешнему поведению, в частности по тому, как он преобразует приходящие на вход сигналы. Если некоторая система слишком сложна, то нет смысла искать её математическое описание. Проще попытаться построить вместо неё другую систему, которая при заданных условиях будет вести себя точно так же. Такое моделирование часто используется при исследовании отдельных систем живых организмов с помощью компьютерной симуляции. Описать работу живого организма уравнениями крайне тяжело или вообще невозможно. Но возможно построить компьютерную схему, которая при подаче на вход определённого стимула давала бы на выходе реакцию, тождественную или близкую к реакции моделируемой системы. Если спектр совпадающих входных и выходных процессов достаточно широк, то можно ожидать, что построенная схема точно воспроизводит исследуемый объект.
Лекция 01.
Понятие моделирования.
Способы представления моделей
Моделирование – способ, процесс замещения оригинала его аналогом (моделью) с последующим изучением свойств и поведения оригинала на модели.
Модель вместо исходного объекта используется в случаях, когда эксперимент опасен, дорог, происходит в неудобном масштабе пространства и времени (долговременен, слишком кратковременен, протяжен ), невозможен, неповторим, ненагляден и т. д. Проиллюстрируем это:
| |
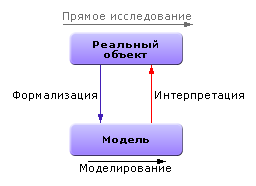
| Рис. 1.1. Процесс моделирования (базовый вариант) |
Если требуется уточнение, эти этапы повторяются вновь и вновь: формализация (проектирование), моделирование, интерпретация. Спираль! Вверх по кругу.
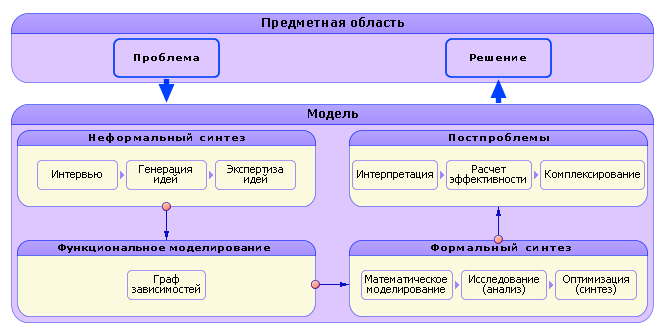
Более подробно весь цикл разработки показан на рис. 1.14, где отражены методы, способы, приёмы, с помощью которых реализуется каждый из этапов.
Поскольку моделирование способ замещения реального объекта его аналогом, то возникает вопрос: насколько аналог должен соответствовать исходному объекту?
Вариант 1: соответствие 100%. Очевидно, что точность решения в этом случае максимальна, а ущерб от применения модели минимален. Но затраты на построение такой модели бесконечно велики, так как объект повторяется во всех своих деталях; фактически, создаётся точно такой же объект путём копирования его до атомов (что само по себе не имеет смысла).
Вариант 2: соответствие 0%. Модель совсем не похожа на реальный объект. Очевидно, что точность решения минимальна, а ущерб от применения модели максимален, бесконечен. Но затраты на построение такой модели нулевые.
Конечно, варианты 1 и 2 это крайности. На самом деле модель создаётся из соображений компромисса между затратами на её построение и ущербом от неточности её применения. Это точка между двумя бесконечностями. То есть, моделируя, следует иметь в виду, что исследователь (моделировщик) должен стремиться к оптимуму суммарных затрат, включающих ущерб от применения и затраты на изготовление модели (см. рис. 1.2 ).
| |
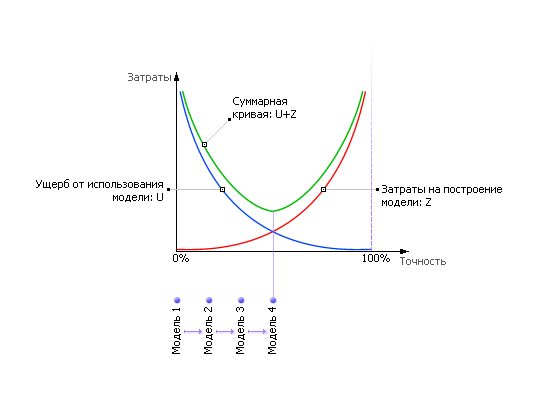
| Рис. 1.2. Соотношение суммарных затрат и точности для различных вариантов детализации прикладной модели |
Просуммируйте две кривые затрат получится одна кривая общих затрат. Найдите оптимум на суммарной кривой: он лежит между этими крайними вариантами. Видно, что неточные модели не нужны, но и абсолютная точность тоже не нужна, да и невозможна. Частое и распространённое заблуждение при построении моделей требовать «как можно точнее».
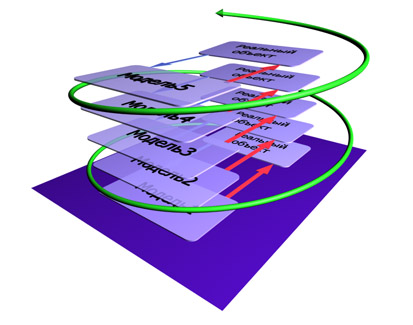
К сожалению, указанная на рис. 1.2 кривая является умозрительной и реально до начала моделирования построена быть не может. Поэтому на практике действуют таким образом: двигаются по шкале точности слева направо, то есть от простых моделей («Модель 1», «Модель 2» ) ко все более сложным («Модель 3», «Модель 4» ). А процесс моделирования имеет циклический спиралевидный характер: если построенная модель не удовлетворяет требованиям точности, то её детализируют, дорабатывают на следующем цикле (см. рис. 1.3 ).
| |
| Рис. 1.3. Спиралевидный характер процесса проектирования и уточнения прикладных моделей |
Улучшая модель, следят, чтобы эффект от усложнения модели превышал связанные с этим затраты. Как только исследователь замечает, что затраты на уточнение модели превышают эффект от точности при применении модели, следует остановиться, поскольку точка оптимума достигнута. Такой подход всегда гарантирует окупаемость вложений.
Из всего сказанного следует, что моделей может быть несколько: приближенная, более точная, ещё точнее и так далее. Модели как бы образуют ряд. Двигаясь от варианта к варианту, исследователь совершенствует модель. Для построения и совершенствования моделей необходима их преемственность, средства отслеживания версий и так далее, то есть моделирование требует инструмента и опирается на технологию.
Инструмент типовое средство, позволяющее достичь оригинальный результат и обеспечивающее сокращение затрат на выполнение промежуточных операций (имиджи, стандартные библиотеки, мастера, линейки, резинки ).
Технология набор стандартных способов, приёмов, методов, позволяющий достичь результата гарантированного качества с помощью указанных инструментов за заранее известное время при заданных затратах, но при соблюдении пользователем объявленных требований и порядка.
Среда совокупность рабочего пространства и инструментов на нем, поддерживающая хранение и изменение, преемственность проектов и интерпретирующая свойства объектов и систем из них.
Иногда модели пишут на языках программирования, но это долгий и дорогой процесс. Для моделирования можно использовать математические пакеты, но, как показывает опыт, в них обычно не хватает многих инженерных инструментов. Оптимальным является использование среды моделирования.
В нашем курсе в качестве такой среды выбрана «Система проектирования и моделирования Stratum-2000». Лабораторные работы и демонстрации, которые вы встретите в курсе, следует запускать как проекты среды Stratum-2000.
Модель, выполненная с учётом возможности её модернизации, конечно, имеет недостатки, например, низкую скорость исполнения кода. Но есть и неоспоримые достоинства. Видна и сохранена структура модели, связи, элементы, подсистемы. Всегда можно вернуться назад и что-то переделать. Сохранен след в истории проектирования модели (но когда модель отлажена, имеет смысл убрать из проекта служебную информацию). В конце концов, модель, которая сдаётся заказчику, может быть оформлена в виде специализированного автоматизированного рабочего места (АРМа), написанного уже на языке программирования, внимание в котором уже, в основном, уделено интерфейсу, скоростным параметрам и другим потребительским свойствам, которые важны для заказчика. АРМ, безусловно, вещь дорогая, поэтому выпускается он только тогда, когда заказчик полностью оттестировал проект в среде моделирования, сделал все замечания и обязуется больше не менять своих требований.
Моделирование является инженерной наукой, технологией решения задач. Это замечание очень важное. Так как технология есть способ достижения результата с известным заранее качеством и гарантированными затратами и сроками, то моделирование, как дисциплина:
Смежными моделированию предметами являются: программирование, математика, исследование операций.
Программирование потому что часто модель реализуют на искусственном носителе (пластилин, вода, кирпичи, математические выражения ), а компьютер является одним из самых универсальных носителей информации и притом активным (имитирует пластилин, воду, кирпичи, считает математические выражения и т. д.). Программирование есть способ изложения алгоритма в языковой форме. Алгоритм один из способов представления (отражения) мысли, процесса, явления в искусственной вычислительной среде, которой является компьютер (фон-Неймановской архитектуры). Специфика алгоритма состоит в отражении последовательности действий. Моделирование может использовать программирование, если моделируемый объект легко описать с точки зрения его поведения. Если легче описать свойства объекта, то использовать программирование затруднительно. Если моделирующая среда построена не на основе фон-Неймановской архитектуры, программирование практически бесполезно.
Какова разница между алгоритмом и моделью?
Алгоритм это процесс решения задачи путём реализации последовательности шагов, тогда как модель совокупность потенциальных свойств объекта. Если к модели поставить вопрос и добавить дополнительные условия в виде исходных данных (связь с другими объектами, начальные условия, ограничения), то она может быть разрешена исследователем относительно неизвестных. Процесс решения задачи может быть представлен алгоритмом (но известны и другие способы решения). Вообще примеры алгоритмов в природе неизвестны, они суть порождение человеческого мозга, разума, способного к установлению плана. Собственно алгоритм это и есть план, развёрнутый в последовательность действий. Следует различать поведение объектов, связанное с естественными причинами, и промысел разума, управляющий ходом движения, предсказывающий результат на основе знания и выбирающий целесообразный вариант поведения.
Математика наука, предоставляющая возможность исчисления моделей, приводимых к стандартному (каноническому) виду. Наука о нахождении решений аналитических моделей (анализ) средствами формальных преобразований.
Исследование операций дисциплина, реализующая способы исследования моделей с точки зрения нахождения наилучших управляющих воздействий на модели (синтез). По большей части имеет дело с аналитическими моделями. Помогает принимать решения, используя построенные модели.
Проектирование процесс создания объекта и его модели; моделирование способ оценки результата проектирования; моделирования без проектирования не существует.
Смежными дисциплинами для моделирования можно признать электротехнику, экономику, биологию, географию и другие в том смысле, что они используют методы моделирования для исследования собственного прикладного объекта (например, модель ландшафта, модель электрической цепи, модель денежных потоков и т. д.).
| |
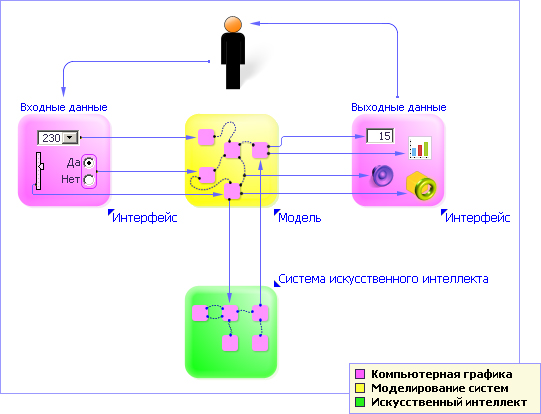
| Рис. 1.4. Основные подсистемы при проектировании комплексных моделей |
Компьютерная графика помогает организовать удобный естественный интерфейс для управления моделью, для наблюдения за её реакциями. Важно понимать, что пользователь взаимодействует с моделью не напрямую, а именно через интерфейс: с одной стороны он посылает ей исходные (входные) данные (например, с помощью окон ввода, кнопок, движков, командной строки и т. д.), с другой смотрит на результат работы модели, то есть воспринимает посредством интерфейса выходные данные.
Искусственный интеллект подразумевает построение высших моделей (например, адаптивных, которые умеют самонастраиваться, умеют создавать друг друга и т. д.). Подразумевается, что модель интеллекта в состоянии сама строить модели прикладных объектов и систем; объяснение того, как это делается, даётся в курсе «Модели и методы искусственного интеллекта». Вместе с тем заметим, что ряд исследователей, говоря об искусственном интеллекте, имеют в виду применение моделей (обучения, воспроизведения, языка и т. д.) для изучения и имитации одной из самых сложных систем во Вселенной человека.
Заметим, что искусственный интеллект достаточно большая модель, которая содержит обширную информацию об окружающем мире и мета-модели, умеющие её достраивать. Мета-модели имеют большое подобие с имитируемым ими человеком.
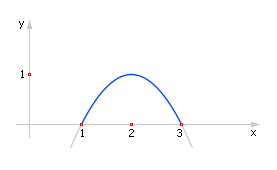
В зависимости от носителя различают модели: натурные, мысленные, математические, имитационные, графические, фотографические и так далее. Каждая из моделей обладает различной способностью к прогнозу свойств объекта. Например, по фотографии человека в анфас вряд ли можно верно представить, как выглядит его затылок. Приближение в виде трёхмерной модели намного лучше, но можно ли с её помощью определить, когда, например, у виртуального человека вырастут волосы длиной 50 см? Имитационная модель ещё более информативна. Но наибольшей ценностью обладают модели, пригодные для решения задач, то есть обладающие прогностическими свойствами, умеющие отвечать на вопросы. Следует различать два понятия «модель» и «задача». Модель связывает переменные между собой законами. Эти законы действуют независимо от того, какая сейчас задача стоит перед нами. Модель объективна, она подобна миру, который нас окружает, и содержит в себе информацию об этом. Структура мира (в общем смысле) неизменна, фундаментальна, модель, следовательно, тоже. А человек, как существо субъективное, имеющее собственные цели, часто меняющиеся желания, ставит, в зависимости от своих потребностей, каждый раз новые задачи, требует решить возникающие у него проблемы. Он ставит вопросы к окружающему миру, с законами которого нельзя не считаться. Удобно ставить вопросы к модели, которая содержит нужную информацию о мире. Поэтому задача это совокупность вопроса и модели. Можно к модели задавать все новые и новые вопросы и при этом не менять модель, но менять задачу.
| |
| Рис. 1.5. Траектория движения тела, брошенного под углом к горизонту |
Теперь модель и вопрос вместе образовали задачу:
Трактовать задачу можно так: при каких значениях x тело окажется на поверхности Земли?
Модель подразумевает, что исследователь может решать с её помощью прямые и обратные задачи.
| |
| Рис. 1.6. Вид модели для решения прямой задачи |
И в первом, и во втором случае мы в разной мере преобразовывали модель, но всегда так, чтобы на входе у неё была известная величина, а на выходе неизвестная.
Способность модели преобразовываться с помощью алгебры даёт возможность в дальнейшем использовать её многократно для решения различных задач, делать на ней прогнозы.
Сравните: телефонный справочник это тоже своеобразная модель, но какие прогнозы вы можете сделать, какие обратные задачи решить? Как вычислить фамилию абонента по номеру телефона? Какую алгебру вы используете?
Поэтому, создавая модель, следует обязательно думать о том, какой алгеброй она будет преобразовываться. Создавать алгебру следует параллельно с моделью или использовать уже готовую алгебру и не отходить при построении модели от её правил.
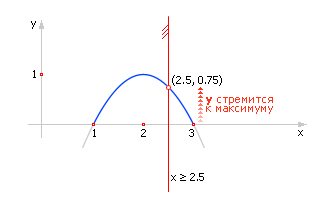
Ещё один тип задач, который приходится решать на моделях задачи настройки модели.
 | y = a · x 2 + 4 · x 3 y = 9 x = 2 |
 | 9 = a · 2 2 + 4 · 2 3 |
| |
| Рис. 1.7. Структурное изображение модели в среде моделирования |
Модель закономерность, преобразующая входные значения в выходные. А как известно из математики, с выражением Y = M(X) можно решить три вида задач, которые приведены в табл. 1.1.
| Таблица 1.1. Формы записи модели и типы решаемых задач | |||||||||||||||
|
В целом получается обратная задача. А то, что надо определить управляемая переменная. То есть интересуются: как следует изменить входной параметр (управление), чтобы обеспечить выполнение законов, не выйти за ограничения и чтобы при этом критерий принял наилучшее значение?
| |
| Рис. 1.8. Графическая иллюстрация решения задачи с ограничениями |
Отметим, что создать модель бывает проще, чем сразу дать себе ответ на интересующий вопрос. Наверное, на практике вы замечали, что часто гораздо проще составить уравнения, чем угадать решение задачи. Например: решено разделить огромный шар размером с Землю на две половинки, полученную половинку снова поделить пополам и так далее. Попробуйте ответить на вопрос: сколько раз ( n ) надо провести такую операцию, чтобы размер делимой частички в результате достиг размера атома? Наверняка, сразу ответить на этот вопрос не удастся, интуиция подводит, придётся составить модель.
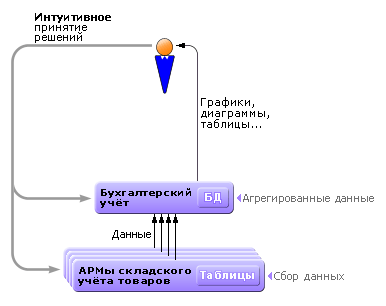
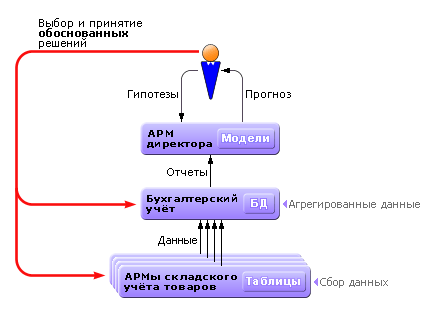
Заметим, что недооценка в современных условиях понятия моделирования ведёт к использованию в АРМах коммерческого назначения только данных. Именно поэтому такие АРМы не способны решать прогностические задачи и решают, в основном, только учётные задачи (см. рис. 1.9 ).
| |
| Рис. 1.9. Типовая схема взаимодействия АРМов в АСУ (без решения задач прогнозирования) |
Чтобы проиграть ситуацию на предприятии на будущее, узнать, к чему приведёт то или иное решение, следует в состав АРМов включать модели (см. рис. 1.10 ).
| |
| Рис. 1.10. Схема взаимодействия АРМов в АСУ (при постановке задач прогнозирования) |
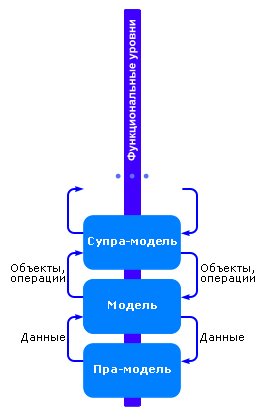
На рис. 1.11 показана пирамида моделей, различных по степени прогностичности.
| |
| Рис. 1.11. Соотношение типов моделей по степени прогностичности |
Обратите внимание: уровень «Модель» «питается» информацией, структурированной по типу предыдущего уровня «Пра-модель», то есть она потребляет на входе данные, перерабатывает их и возвращает тоже данные, то есть модели более низкого уровня (пра-модели). Подчеркнём ещё раз, что данные это тоже модели! Уровень «Супра-модель» потребляет на входе модели в виде объектов и операций, перерабатывает их и возвращает модели (примером таких супра-моделей могут служить грамматики, способные преобразовывать модели (уравнения). Более детально см. рис. 1.12). Данный принцип справедлив и для всех последующих (вышестоящих) уровней. Пирамида на рис. 1.11 представлена в виде функциональных уровней; это означает, что каждый последующий уровень мощнее предыдущего, то есть он позволяет получить больший, более мощный качественный результат.
Модели могут принимать различную форму, в зависимости от способа мышления исследователя, его взгляда на мир, используемой алгебры. Использование различных математических аппаратов впоследствии приводит к различным возможностям в решении задач.
Феноменологические модели сильно привязаны к конкретному явлению. Изменение ситуации часто приводит к тому, что моделью воспользоваться в новых условиях достаточно сложно. Это происходит оттого, что при составлении модели её не удалось построить с точки зрения подобия внутреннему строению моделируемой системы. Феноменологическая модель передаёт внешнее подобие.
Абстрактная модель воспроизводит систему с точки зрения её внутреннего устройства, копирует её более точно. У неё больше возможностей, шире класс решаемых задач.
Активные модели взаимодействуют с пользователем; могут не только, как пассивные, выдавать ответы на вопросы пользователя, когда тот об этом попросит, но и сами активируют диалог, меняют его линию, имеют собственные цели. Все это происходит за счёт того, что активные модели могут самоизменяться.
Статические модели описывают явления без развития. Динамические модели прослеживают поведение систем, поэтому используют в своей записи, например, дифференциальные уравнения, производные от времени.
Дискретные и непрерывные модели. Дискретные модели изменяют состояние переменных скачком, потому что не имеют детального описания связи причин и следствий, часть процесса скрыта от исследователя. Непрерывные модели более точны, содержат в себе информацию о деталях перехода.
Детерминированные и стохастические модели. Если следствие точно определено причиной, то модель представляет процесс детерминировано. Если из-за неизученности деталей не удаётся описать точно связь причин и следствий, а возможно только описание в целом, статистически (что часто и бывает для сложных систем), то модель строится с использованием понятия вероятности.
Распределённые, структурные, сосредоточенные модели. Если параметр, описывающий свойство объекта, в любых его точках имеет одинаковое значение (хотя может меняться во времени!), то это система с сосредоточенными параметрами. Если параметр принимает разные значения в разных точках объекта, то говорят, что он распределён, а модель, описывающая объект, распределённая. Иногда модель копирует структуру объекта, но параметры объекта сосредоточенны, тогда модель структурная.
Функциональные и объектные модели. Если описание идёт с точки зрения поведения, то модель построена по функциональному признаку. Если описание каждого объекта отделено от описания другого объекта, если описываются свойства объекта, из которых вытекает его поведение, то модель является объектно-ориентированной.
Каждый подход имеет свои достоинства и недостатки. Разные математические аппараты имеют разные возможности (мощность) для решения задач, разные потребности в вычислительных ресурсах. Один и тот же объект может быть описан различными способами. Инженер должен грамотно применять то или иное представление, исходя из текущих условий и стоящей перед ним проблемы.
Приведённая выше классификация является идеальной. Модели сложных систем обычно имеют комплексный вид, используют в своём составе сразу несколько представлений. Если удаётся свести модель к одному типу, для которого уже сформулирована алгебра, то исследование модели, решение задач на ней существенно упрощается, становится типовым. Для этого модель должна быть различными способами (упрощением, переобозначением и другими) приведена к каноническому виду, то есть к виду, для которого уже сформулирована алгебра, её методы. В зависимости от используемого типа модели (алгебраические, дифференциальные, графы и т. д.) на разных этапах её исследования используются различные математические аппараты.
| |
| Рис. 1.13. Схема процесса моделирования (уточнённый вариант) |
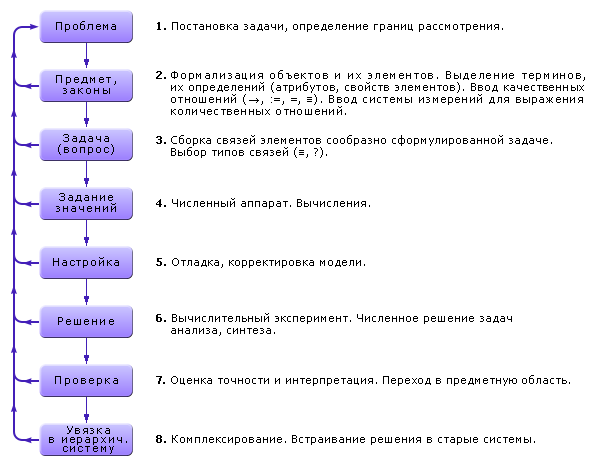
На рис. 1.15 представлены этапы построения модели.
| |
| Рис. 1.15. Этапы процесса моделирования |
Общее описание технологии моделирования расположено в файле справки системы «Stratum-2000» в разделе «Теория моделирования» («Помощь» > «Теория моделирования»). Сначала данный раздел стоит прочитать бегло, а затем подробно после того, как вы усвоите весь курс и накопите опыт описания объектов на примерах и опыте, приобретённом в ходе выполнения курсовой работы.
Здесь можно упомянуть два направления. Первое инструментальное. Проектировщику необходим инструмент для формального описания рассматриваемого им объекта. Известно несколько таких инструментов: RationalRose, «Аналитик», IDEF по технологии SADT, Stratum. Есть инструменты, подсказывающие решения, есть просто пассивные наборы, библиотеки. Одним из инструментов нахождения решений является технология АЛРИЗ; следуя её алгоритму, отвечая на вопросы этой технологии, можно гарантированно придти к решению.
Второй путь аналитические системы, выводящие из фактов знания. О них пойдёт речь в следующем нашем курсе «Модели и методы искусственного интеллекта».
В качестве примера посмотрим, как можно обнаружить, а потом описать закономерность.
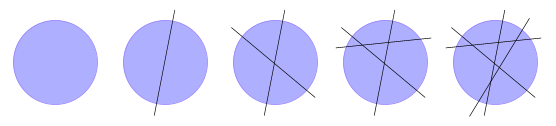
Допустим, что нам нужно решить «Задачу о разрезаниях», то есть надо предсказать, сколько потребуется разрезов в виде прямых линий, чтобы разделить фигуру ( рис. 1.16 ) на заданное число кусков (для примера достаточно, чтобы фигура была выпуклой).
Попробуем решить эту задачу вручную.
| |
| Рис. 1.16. Задача о разрезании фигуры на заданное число кусков |
Составим таблицу, связывающую известные нам числа кусков и разрезов.
| Таблица 1.2. Таблица соответствия разрезов и получающихся фрагментов фигуры | ||||||||||||
|
| Таблица 1.3. Таблица соответствия разрезов и получающихся фрагментов фигуры | ||||||||||||||||||
|
Уже кое-какая закономерность проявилась, не правда ли?
Вычислим вторые разности.
| Таблица 1.4. Таблица соответствия разрезов и получающихся фрагментов фигуры | |||||||||||||||||||||||
|
Очевидно, что далее продолжать процедуру вычисления разностей смысла нет.
Функция f есть частный случай формулы Ньютона:
| Таблица 1.5. Таблица соответствия разрезов и получающихся фрагментов фигуры | |||||||||||||||||||||||
|
Итак, закономерность есть, и она такова:
Подведём итоги (обратите на это внимание!).
Сразу угадать решение мы не смогли. Поставить эксперимент оказалось затруднительно. Пришлось построить модель, то есть найти закономерность между переменными. Модель получилась в виде уравнения. Добавив к уравнению вопрос и уравнение, отражающее известное условие, образовали задачу. Поскольку задача оказалась типового вида (канонического), то её удалось решить одним из известных методов. Поэтому задача оказалась решена.
И ещё очень важно отметить, что модель отражает причинно-следственные связи. Между переменными построенной модели действительно есть крепкая связь. Изменение одной переменной влечёт за собой изменение другой. Мы ранее сказали, что «модель играет системообразующую и смыслообразующую роль в научном познании, позволяет понять явление, структуру изучаемого объекта, установить связь причины и следствия между собой». Это означает, что модель позволяет определить причины явлений, характер взаимодействия её составляющих. Модель связывает причины и следствия через законы, то есть переменные связываются между собой через уравнения или выражения.
Но. Сама математика не даёт возможности выводить из результатов экспериментов какие-либо законы или модели, как это может показаться после рассмотренного только что примера. Математика это только способ изучения объекта, явления, и, причём, один из нескольких возможных способов мышления. Есть ещё, например, религиозный способ или способ, которым пользуются художники, эмоционально-интуитивный, с помощью этих способов тоже познают мир, природу, людей, себя.
Итак, гипотезу о связи переменных А и В надо вносить самому исследователю, извне, сверх того. А как это делает человек? Посоветовать внести гипотезу легко, но как научить этому, объяснить это действо, а значит, опять-таки как его формализовать? Подробно мы покажем это в будущем курсе «Моделирование систем искусственного интеллекта».
А пока, чтобы «не подорваться на ерунде», вам надо быть настороже и проверять все здравым смыслом. Приведём пример, старую известную шутку из фольклора физиков.
Огурцы вас погубят! Каждый съеденный огурец приближает вас к смерти. Удивительно, как думающие люди до сих пор не распознали смертоносности этого растительного продукта и даже прибегают к его названию для сравнения в положительном смысле («как огурчик!»). И, несмотря ни на что, производство консервированных огурцов растёт.
С огурцами связаны все телесные недуги и вообще все людские несчастья.
Есть данные и о том, что вредное действие огурцов сказывается очень долго: среди людей, родившихся в 1889 году и питавшихся впоследствии огурцами, смертность равна 100%. Все лица рождения 18891909 годов имеют дряблую морщинистую кожу, потеряли почти все зубы, практически ослепли (если болезни, вызванные потреблением огурцов, не свели их уже давно в могилу).
Ещё более убедительный результат, полученный известным коллективом учёных-медиков: морские свинки, которым принудительно скармливали по 20 фунтов огурцов в день в течение месяца, потеряли аппетит!
Единственный способ избежать вредного действия огурцов изменить диету. Ешьте суп из болотных орхидей. От него, насколько нам известно, ещё никто не умирал.
Движемся дальше. Сложность задачи часто диктует тот способ представления модели, который будет использоваться при её описании. Покажем это на примере простейшей задачи.
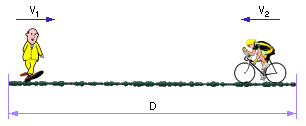
Задача 1. Пусть два объекта (например, пешеход и велосипедист) движутся друг другу навстречу ( рис. 1.17 ) со скоростями V1 и V2 соответственно. Необходимо узнать: когда и где встретятся эти объекты?
| |
| Рис. 1.17. Задача о встрече |
Аналитический способ представления задачи 1
Аналитический явный способ
|
| |
| Рис. 1.18. Схема решения задачи о встрече (аналитический явный способ) |
Аналитический неявный способ
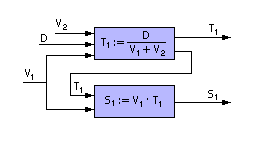
В данной формулировке за счёт использования знака уравнивания получена связь переменных f(T, V1, V2, D, S) = 0 в виде системы уравнений. Устанавливая знак «?» на различные переменные, можно формулировать при необходимости целый ряд произвольных задач, например так:
При этом задачи формулируются пользователем и не предусматриваются специально моделировщиком. То есть модель имеет вид объекта. Мы получили более качественную модель. Идеализация её велика, но за счёт неявной формы записи появилась возможность изменения задачи, изучения на ней целого ряда проблем.
Имитационный способ представления задачи 1
При имитационном способе решения обязательным является наличие некоего счётчика, который позволяет моделировать процесс по шагам или по деталям процесса.
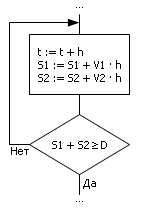
Имитационный алгоритмический способ
| |
| Рис. 1.19. Блок-схема решения задачи о встрече (имитационный алгоритмический способ) |
На формально-математическом языке алгоритм выглядит так, как показано ниже.
|
|
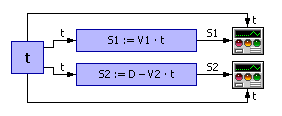
Имитационный геометрический способ
| |
| Рис. 1.20. Схема решения задачи о встрече (имитационный геометрический способ) |
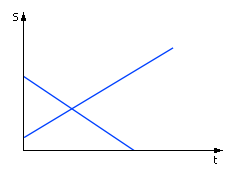
На рис. 1.21 вы видите картину, образованную двумя осциллограммами. Точка, в которой пересекаются осциллограммы, является предполагаемой точкой встречи двух объектов.
| |
| Рис. 1.21. Вид решения задачи о встрече (имитационный геометрический способ) |
Имитационная статистическая постановка задачи
Главное отличие имитационных моделей от аналитических, которые мы рассмотрели выше, состоит в том, что имитационную модель можно постепенно усложнять, при этом результативность модели не падает.
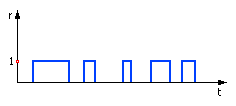
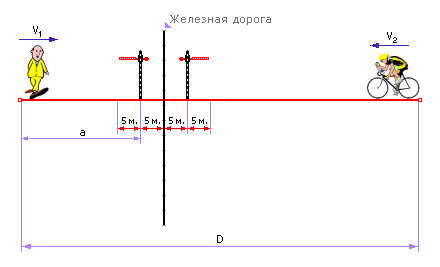
Усложним задачу 1, введя в неё дополнительное условие. Представим, что на пути первого и/или второго объекта встретится помеха пусть это будет участок железной дороги со шлагбаумом, который работает по случайному закону. Если шлагбаум открыт, то объект может переходить железную дорогу, в противном случае он не имеет права этого делать.
| |
| Рис. 1.22. Вид функции случайных помех (к задаче о встрече) |
На рис. 1.23 дана иллюстрация усложнённой задачи 1.
| |
| Рис. 1.23. Иллюстрация к усложнённой задаче о встрече |
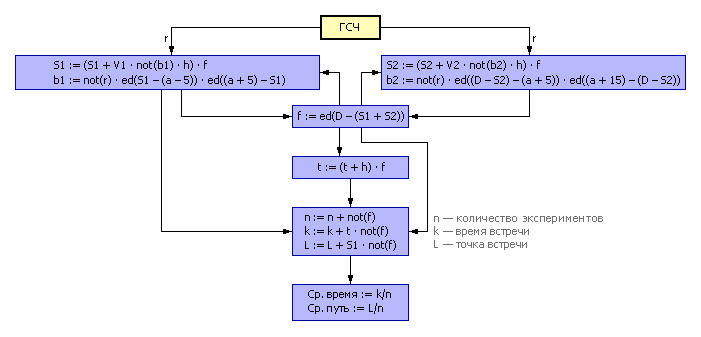
На рис. 1.24 представлена алгоритмическая схема задачи.
| |
| Рис. 1.24. Схема решения задачи о встрече (имитационный статистический способ) |
Поскольку алгоритм использует случайные числа в качестве исходных данных, придётся сделать несколько экспериментов и найти средние значения выходных величин. Результат одного эксперимента случаен и ни о чем не говорит. Среднее значение более информативно. Ещё более информативны сведения о первом и втором моменте среднем и разбросе значений вокруг него (дисперсии) и так далее.
Имитационный критериальный способ
Этот способ ещё один шаг к усложнению модели и приближению её к реальным условиям. Если во всех предыдущих случаях скорость V была известна, то теперь она непредсказуема, даже статистически, что чаще всего и наблюдается в реальных условиях. Скорость V объекта принимается из некоторых дополнительных моделей. Причём эти модели могут быть с обратными связями. Например, скорость может зависеть от обстановки, степени достижения цели, плана, целесообразности поведения, знания местности, желания двигаться (психологический мотив). Такая постановка ведёт к адаптивным системам и системам искусственного интеллекта.
Например, если объект (пешеход) имеет возможность осмотреть местность с обзорной башни, то он может заранее просчитать свой путь и затем следовать ему. Без обзорной башни пешеход может зайти в безвыходный тупик или бесконечно долго перебирать варианты пути. Для адаптивных систем вводится критерий для оценки перспективности выбора направления движения.
Итак, подведём итог.
Модель способ замещения реального объекта, используемый для его исследования, когда натуральный эксперимент невозможен, дорог, опасен, долговременен.
Примеры. Поскольку исследование Луны небезопасно для человека, для этой цели используют луноход как модель исследователя; поскольку реальные эксперименты над экономикой страны дороги по своим последствиям, то используют математические модели экономики для изучения последствий управляющих решений; поскольку процесс обработки металлов взрывом скоротечен во времени, то его изучают на модели в увеличенном масштабе времени, а процесс коррозии в уменьшенном; атом изучается в увеличенном масштабе пространства, а космогонические процессы в уменьшенном масштабе пространства; поскольку при проектировании объекта его попросту не существует, то исследование будущих свойств объекта ведётся на модели.
Модель несёт системообразующую и смыслообразующую роль в научном познании. На модели изучают неизвестные свойства предметов. Модель стремится как можно более ярко выразить структуру явления, его главные аспекты. Модель является концентрированным выражением сущности предмета или процесса, выделяя только его основные черты.
Знания это модели окружающего мира, фиксируемые человеком в его мозгу или на технических носителях. Модели обладают повышенной наглядностью, выделяя главные аспекты сущности, и активно используются в процессах познания и обучения. Человек, решая, как ему поступить в той или иной ситуации, всегда пытается представить себе последствия решения, для этого он проигрывает ситуацию, представляет её себе мысленно, строя модель в голове. Компьютер является усилителем для производства данной деятельности, инструментом информационной технологии. Компьютерные модели ускоряют процесс исследования, делают его более точным.
Алгоритмы знания, выстраиваемые человеком (или, шире, разумным существом) в цепочку так, чтобы соединить исходное состояние с желаемым, целью; это один из вариантов ряда мероприятий, шагов, приводящих к цели.
Таким образом, модели это основа разумной мыслительной деятельности; модели играют роль базиса, а моделирование роль инструмента для прогнозирования.
Процесс моделирования состоит из трёх стадий: формализации (переход от реального объекта к модели), моделирования (исследование и преобразования модели), интерпретации (перевод результатов моделирования в область реальности).
Набор моделей образует научную дисциплину (механика, физика, горное дело и т. д.) Модель может быть расширена путём учёта в ней дополнительных параметров. Тогда область её применения становится шире.
Объект может быть представлен в виде аналитической или имитационной модели.
Аналитическое представление подходит лишь для очень простых и сильно идеализированных задач и объектов, которые, как правило, имеют мало общего с реальной (сложной) действительностью, но обладают высокой общностью. Аналитические модели обычно применяют для описания фундаментальных свойств объектов (поэтому ими так широко пользуется теоретическая физика), так как фундамент прост по своей сути. Сложные объекты редко удаётся описать аналитически.
Имитационное моделирование позволяет разлагать большую модель на части (объекты, «кусочки»), которыми можно оперировать по отдельности, создавая другие, более простые или, наоборот, более сложные модели. Таким образом, имитационное моделирование тяготеет к объектно-ориентированному представлению, которое естественным образом описывает объекты, их состояние, поведение, а также взаимодействие между ними. Имитационную модель можно постепенно усложнять и усложнять; аналитический способ этого не допускает или допускает, но с большими ограничениями.
Модель может быть соединена с другими моделями. Математически это означает совместное решение моделей (пересечение) и наложение тождеств на связываемые переменные. При связывании модели образуют систему, которая имеет определённую структуру (вложенную, параллельную, последовательную, смешанную, с обратными связями и т. д.)
Если к построенной модели добавить вопрос, то с помощью неё можно решить задачу, получить ответ, который заранее не очевиден. Если ответ заранее очевиден, то модель не строят. Обычно одна и та же модель годится для решения множества задач. Решая задачи, человек обычно строит модели в своей голове и оживляет (интерпретирует) их там же или на искусственном носителе (в среде моделирования).
В виде условий могут быть любые дополнительные выражения: равенства, присваивания начальных данных, неравенства, цели, функционалы и т. д., имеющие смысл ограничений, условий, дополнительных связей.
В виде вопроса может служить одна (или несколько) из неизвестных переменных.
Задача доопределяет свободные переменные модели, сужает область возможных решений.
Роль модели
Построив модель, исследователь может:
Адекватность модели
Поскольку модель является выражением конечного ряда и только важнейших для конкретного исследования аспектов сущности, то она не может быть абсолютно идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для познания. Поэтому нет смысла стремиться к бесконечной точности при построении модели. Для выяснения необходимой степени адекватности обычно строят ряд моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и точным. Как только затраты на построение очередной модели начинают превышать планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные шаги производятся в каком-либо существующем универсальном моделирующем пакете. После одобрения модели под неё пишется специализированный пакет. Необходимость в этом возникает в случае, если функционирование модели в универсальной среде моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).
В задачи данного курса входит изучение приёмов и способов, необходимых для формализации, изучения и интерпретации систем.
Моделирование прикладная инженерная наука класса технологических. Моделирование дисциплина, ставящая целью построение моделей и их исследование посредством собственных универсальных методов, а также специфических методов смежных с ней наук (математика, исследование операций, программирование).