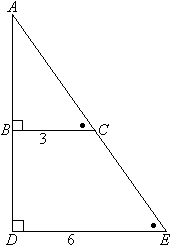На что похож треугольник
Презентация «Игра «Найди предмет, похожий на треугольник»
Если ребёнок захочет повторить свой успех, то на последнем слайде также необходимо нажать на треугольник в правом нижнем углу слайда и игра начнётся сначала.
Прикреплённые файлы:


Дидактическая игра-занятие «Отгадай предмет» (младшая группа) Дидактическая игра-занятие «Отгадай предмет» младшая группа (дети 3–4 года) Цель игры: описывать предметы,выделяя признаки: материал, основные.
Игра «Найди клад» Задачи: 1. Развивать у детей умение ориентироваться на местности используя рисунок (карту). 2. Формировать дружеские и доброжелательные.
Презентация «Игра «Найди лишнее» для развития мышления и речи дошкольников» Мышление — это процесс анализа и систематизации новой информации об окружающем мире, полученной с помощью органов чувств. Человек наделен.
Презентация к дидактической игре по математике «Найди на картинке и сосчитай» для детей 6–7 лет Презентация к дидактической игре по математике «Найди на картинке и сосчитай» для детей 6-7 лет. Назначение игры – закрепление знаний детей.
Подобие треугольников (ЕГЭ — 2022)
Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.
А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?
Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!
Читай эту статью, смотри вебинар по 16 задаче и все поймешь!
Подобие треугольников — коротко о главном
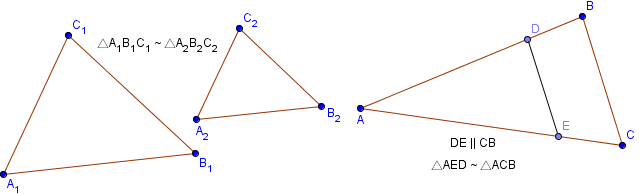
Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия \( \displaystyle k\).
\( \angle A = \angle
Отношение периметров подобных треугольников равно коэффициенту подобия: \( \displaystyle \frac<<
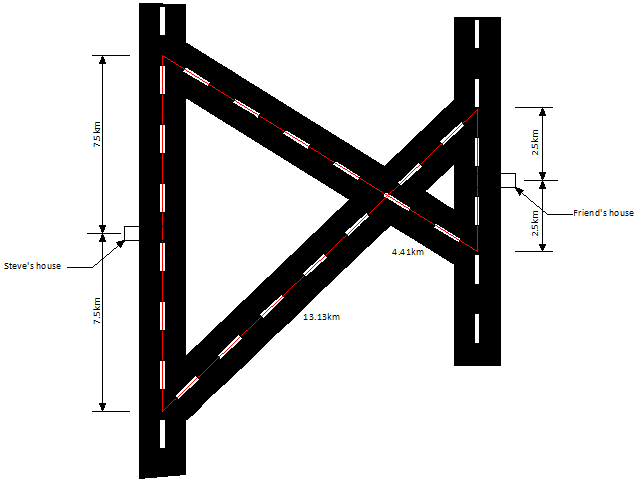
_ _<<_<1>><_<1>>< Отношение площадей подобных треугольников равно квадрату коэффициента подобия: \( \displaystyle \frac<< Признаки подобия треугольников: По двум углам: По одному углу и отношению заключающих его сторон: По отношению трех сторон: Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы: Но что такое подобные треугольники? Вот, например, такой и такой: Похожи эти треугольники? Ты скажешь, конечно же нет! А вот такой и такой? Посмотри внимательно, тоже похожи. А теперь строго математически! Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны. То есть все углы равны и все стороны одного треугольника в \( \displaystyle 5\), или, в \( \displaystyle 7\), или в \( \displaystyle 8,21\) (или и т.д.) больше сторон другого треугольника. Записываются слова «треугольник \( \displaystyle ABC\) подобен треугольнику \( \displaystyle <_<1>><_<1>>< То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы \( \displaystyle k\). \(\angle A = \angle Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон. Помнишь еще, что «\( \displaystyle \sim<\ >\)» обозначает слова «подобен»? Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак. Но есть и еще два. Смотри. Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным? Ну вот, что же хорошего? А то, что тогда… Все элементы одного треугольника ровно в \( \displaystyle 2\) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника. Не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д. Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы. В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение. Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем. Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств). Проанализируем пару треугольников, которые визуально похожи. Стороны второго треугольника в соотношении со сторонами первого меньше в два раза: Под соотношением отрезков AB и А1В1 понимается соотношение их длин. Если соотношения пар отрезков равны, то указывают, что отрезки пропорциональны: У представленных треугольников углы попарно тождественны. Стороны, расположенные напротив одинаковых углов, соразмерны. Такие треугольники именуют подобными. Стороны, расположенные напротив одинаковых углов, принято обозначать как сходственные. Следовательно, подобными называются треугольники, у которых углы попарно тождественны, а сходственные стороны соразмерны. Подобие треугольников обозначается так: Соотношение сходственных сторон подобных фигур именуют коэффициентом подобия. В представленном примере он равен двум. Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты. Два треугольника являются подобными если: 1. Каждый угол одного треугольника равен соответствующему углу другого треугольника: 2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой: Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников: Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными. Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации: 1) три угла каждого треугольника (длины сторон треугольников знать не нужно). 2) длины сторон каждого треугольника (углы знать не нужно); 3) длины двух сторон и угол между ними. Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников. Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными. Решение: Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR. Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно: Пример №3: Определите длину AB в данном треугольнике. Решение: ∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными. $\frac Пример №4:Определить длину AD (x) геометрической фигуры на рисунке. Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C. AB || DE, CD || AC и BC || EC Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны. Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1. Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера. Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень. Решение: Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке. Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно, Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта. А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом: Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем. Решение: Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке. Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно: В условии задачи сказано, что: AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км Используя эту информацию, мы можем вычислить следующие расстояния: Стив может добраться к дому своего друга по следующим маршрутам: Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву. Пример 7: Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания. Решение: Геометрическое представление задачи показано на рисунке. Сначала мы используем подобность треугольников ΔABC и ΔADE. $\frac Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант. Например, все круги похожи друг на друга, все квадраты похожи друг на друга, а все равносторонние треугольники похожи друг на друга. С другой стороны, не все эллипсы похожи друг на друга, не все прямоугольники похожи друг на друга, а не все равнобедренные треугольники похожи друг на друга. Если два угла треугольника имеют меры, равные размерам двух углов другого треугольника, то треугольники подобны. Соответствующие стороны подобных многоугольников пропорциональны, а соответствующие углы подобных многоугольников имеют одинаковую меру. В этой статье предполагается, что масштабирование может иметь коэффициент масштабирования 1, так что все конгруэнтные формы также похожи, но некоторые школьные учебники специально исключают конгруэнтные треугольники из своего определения похожих треугольников, настаивая на том, что размеры должны быть разными, если треугольники должны квалифицируются как аналогичные. [ необходима цитата ] Есть несколько утверждений, каждое из которых необходимо и достаточно для того, чтобы два треугольника были похожими: Когда два треугольника △ ABC и △ A′B′C ′ подобны, пишется [9] : с. 22 Есть несколько элементарных результатов о подобных треугольниках в евклидовой геометрии: [10] Понятие подобия распространяется на многоугольники с более чем тремя сторонами. Для любых двух похожих многоугольников соответствующие стороны, взятые в одной и той же последовательности (даже если по часовой стрелке для одного многоугольника и против часовой стрелки для другого), пропорциональны, а соответствующие углы, взятые в той же последовательности, равны по мере. Однако пропорциональности соответствующих сторон недостаточно для доказательства подобия многоугольников за пределами треугольников (в противном случае, например, все ромбы были бы подобны). Точно так же равенства всех углов в последовательности недостаточно, чтобы гарантировать подобие (в противном случае все прямоугольники были бы подобны). Достаточным условием подобия многоугольников является пропорциональность соответствующих сторон и диагоналей. Некоторые типы кривых обладают тем свойством, что все примеры этого типа похожи друг на друга. К ним относятся: Сходства сохраняют плоскости, линии, перпендикулярность, параллельность, середины, неравенства между расстояниями и отрезками линий. [19] Сходства сохраняют углы, но не обязательно сохраняют ориентацию, прямые подобия сохраняют ориентацию, а противоположные подобия изменяют ее. [20] Эта более слабая версия применяется, когда метрика является эффективным сопротивлением на топологически самоподобном множестве. Эти самоподобные множества имеют автомодельную меру μ D размерности D, задаваемой формулой ∑ s ∈ S ( р s ) D знак равно 1 <\displaystyle \sum _ Определение сходства может варьироваться среди авторов в зависимости от желаемых свойств. Основные общие свойства: Интуиция к понятию геометрического подобия уже появляется у человеческих детей, как это видно на их рисунках. [24]__<<_<1>><_<1>><Подобные треугольники — подробнее
Признак подобия треугольников «по двум углам»
Признак подобия треугольников «две пропорциональные стороны и угол между ними»
Признак подобия треугольников «три пропорциональные стороны»
Самый главный «секрет» подобия треугольников
Читать далее…
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Треугольник. Подобные треугольники. Свойства подобных треугольников.
.
Подобные треугольники
Определение
∠A1 = ∠A2, ∠B1 = ∠B2 и∠C1 = ∠C2
$\fracПрактические задачи с подобными треугольниками
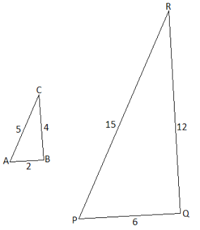
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:
$\frac
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.
∠BAC = ∠EDC и ∠ABC = ∠DECПрактические примеры
$\frac
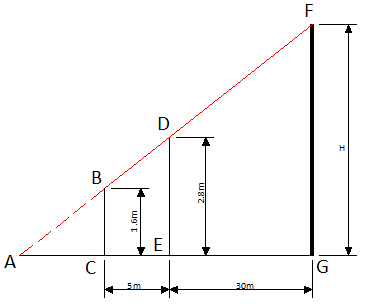
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.
Сходство (геометрия)
СОДЕРЖАНИЕ
Подобные треугольники [ править ]
Другие похожие многоугольники [ править ]
Подобные кривые [ править ]
В евклидовом пространстве [ править ]
Соотношения сторон, площадей и объемов [ править ]
В общих метрических пространствах [ править ]
)^Топология [ править ]
Самоподобие [ править ]
Психология [ править ]