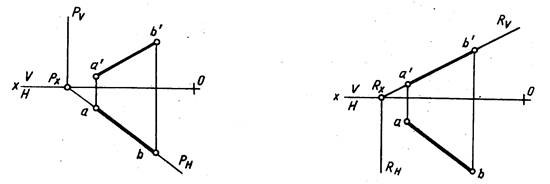на каком эпюре задана плоскость
СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЭПЮРЕ
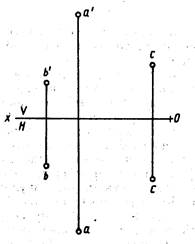
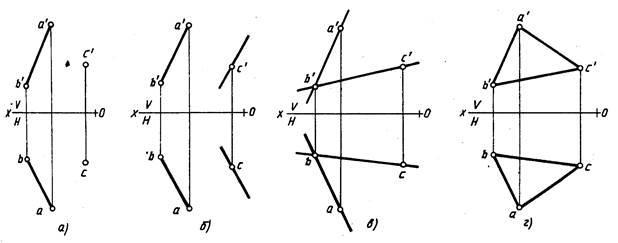
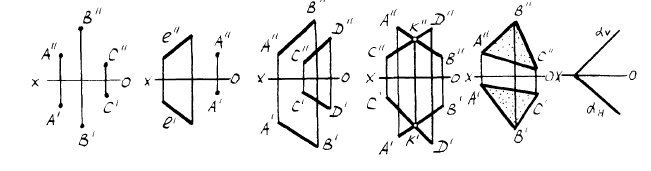
Положение плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой. Поэтому чтобы задать на эпюре плоскость, достаточно задать три ее точки (рис. 206). Плоскость можно задать точкой и прямой (рис. 207, а), двумя параллельными прямыми (рис. 207, б), двумя пересекающимися прямыми (рис. 207, в), треугольником (рис. 207, г).
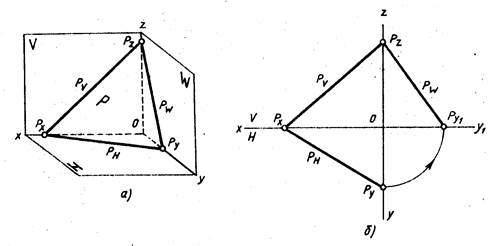
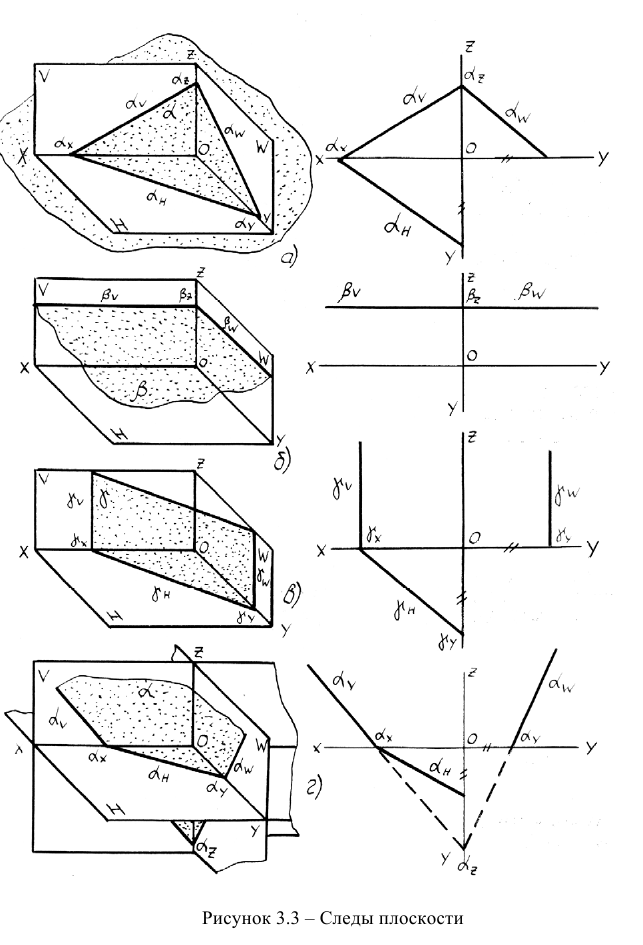
Можно задать плоскость следами. Следом плоскости называют прямую, по которой данная плоскость пересекает плоскость проекций. На рис. 208 Pv — фронтальный след плоскости Р, Рн — горизонтальный след плоскости Р, Pw — профильный след плоскости Р.
Различные случаи расположения плоскостей относительно плоскостей проекций
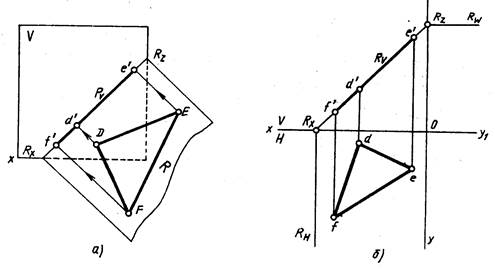
Плоскость общего положения — плоскость, расположенная наклонно ко всем плоскостям проекций (рис. 208). Такая плоскость пересекается с тремя плоскостями проекций по прямым, которые являются следами этой плоскости. Каждая пара следов сходится в точке, которая называется точкой схода следов плоскости и располагается на оси проекций. Плоскость общего положения имеет три точки схода, которые обозначаются Рх, Ру, Рz. В этих точках плоскость пересекает оси координат. Плоские фигуры, лежащие в плоскости общего положения, проецируются проекций с искажением.
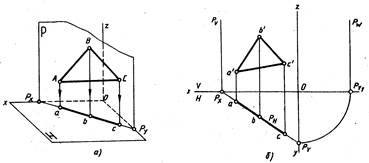
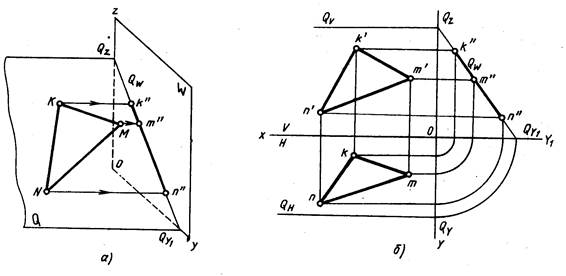
Проецирующая плоскость проецируется на плоскость проекций, к которой она перпендикулярна, в прямую. Па рис. 209 плоскость Р горизонтально-проецирующая, ΔАВС, лежащий в плоскости Р, проецируется в отрезок прямой линии, который совпадает со следом плоскости Рн. На рис. 210 ΔDEF, принадлежащий фронтально-проецирующей плоскости R, проецируется в отрезок, совпадающий со следом плоскости Rv. На рис. 211 ΔKMN, лежащий в профильно-проецирующей плоскости Q, проецируется на плоскость W в отрезок, совпадающий со следом плоскости Qw. Поэтому проецирующие плоскости часто используются в качестве вспомогательных при различных построениях. Например, чтобы через прямую AB провести горизонтально-проецирующую плоскость (рис. 212), достаточно через горизонтальную проекцию прямой ab провести горизонтальный след этой плоскости, так как все, что в этой плоскости лежит, в том числе и прямая AB, проецируется на ее горизонтальный след. Фронтальный след фронтально-проецирующей плоскости совпадает с фронтальной проекцией прямой a’b’ (рис. 213). Следы проецирующих плоскостей на других плоскостях проекций перпендикулярны соответствующим осям проекций (см. рис. 209, 210, 211).
Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости проекций. Геометрические фигуры, лежащие в этих плоскостях, проецируются без искажения на ту плоскость проекций, которой параллельна данная плоскость (рис. 214, 215; 216). Называются такие плоскости так же, как и плоскость проекций, параллельно которой они расположены: горизонтальная плоскость (рис. 214), фронтальная плоскость (рис. 215), профильная плоскость (рис. 216).
На каком эпюре задана плоскость
Способы задания плоскости на эпюре
Из курса элементарной геометрии известно, что через три точки не лежащие на одной прямой можно провести плоскость и при том только одну. Таким образом, положение плоскости в пространстве логично определить (задать) тремя точками (точки А, В, С, табл. 3.1, п1.)
Кроме этого, положение плоскости в пространстве определяют: прямая АВ и точка С, не лежащая на прямой (табл. 3.1, п.2), две пересекающиеся прямые АВ и CD (табл. 3.1, п.3), две параллельные прямые АВ и CD (табл. 3.1, п.4), плоская фигура, т.е. часть плоскости, ограниченная линиями (треугольник, квадрат, круг, ромб и т.д.).
На эпюре (табл. 3.1) плоскость может быть задана соответственно проекциями трех точек, не лежащих на одной прямой, прямой и точки, не лежащей на прямой, двух пересекающихся или параллельных прямых, проекцией плоской фигуры.
Плоскости условимся обозначать прописными латинскими буквами, следующими за буквой P по алфавиту: R, S, T и т.д.
Таблица 3.1 Способы задания плоскости в пространстве и на эпюре
Задание плоскости в пространстве
Задание плоскости на эпюре
Тремя точками, не лежащими на одной прямой
Проекциями трех точек, не лежащих на одной прямой
Прямой и точкой, не лежащей на прямой
Проекциями прямой и точки, не лежащими на одной прямой
Двумя пересекающимися прямыми
Проекциями двух пересекающихся прямых
Двумя параллельными прямыми
Проекциями двух параллельных прямых
Проекциями плоской фигуры
Положение плоскости в пространстве может быть определено ее следами. Следами плоскости называются прямые линии, по которым данная плоскость пересекается с плоскостями проекций.
В общем случае плоскость имеет три следа – горизонтальный, фронтальный и профильный.
На рис. 3.1. и в таблице 3.1. п.6 они обозначены соответственно P1, P2, P3 (буквой Р обозначена заданная плоскость, а индексы 1, 2, 3 означают, с какой из плоскостей проекций пересекается плоскость Р).
В точках Px, Py, Pz, лежащих на осях координат, следы плоскости пересекаются. Эти точки называются точками схода следов плоскости.
Следы плоскости всегда можно построить, если положение плоскости в пространстве задано одним из перечисленных выше способов.
Если прямая АВ (рис.3.1. а и б) лежит в плоскости Р, то она пересечет плоскость П1 в точке М1 расположенной на линии Р1, т.е. горизонтальный след прямой, лежащей в плоскости, расположен на горизонтальном следе плоскости.
Плоскость П2 прямая АВ пересечет в точке N, расположенной на линии Р2.
Иными словами, следы прямой, лежащей в плоскости, расположены на одноименных следах плоскости.
Отсюда следует, что следы плоскости должны проходить через одноименные следы прямых, лежащих в плоскости.
Чтобы построить след плоскости, необходимо определить следы двух прямых, лежащих в плоскости.
На рис. 3.1. плоскость задана двумя пересекающимися прямыми АВ и СD. Чтобы построить горизонтальный след плоскости необходимо найти горизонтальный след прямой АВ – точку М и прямой СD – точку М1. Горизонтальный след плоскости будет проходить через точки М и М1.
Фронтальный след плоскости Р2 строится аналогично. Следует отметить, что для построения следа Р2 достаточно иметь фронтальный след только одной прямой, так как второй точкой, определяющей положение следа Р2 будет точка Рх схода следов (точка пересечения ранее построенного следа Р1 с осью х).
Эпюра плоскости
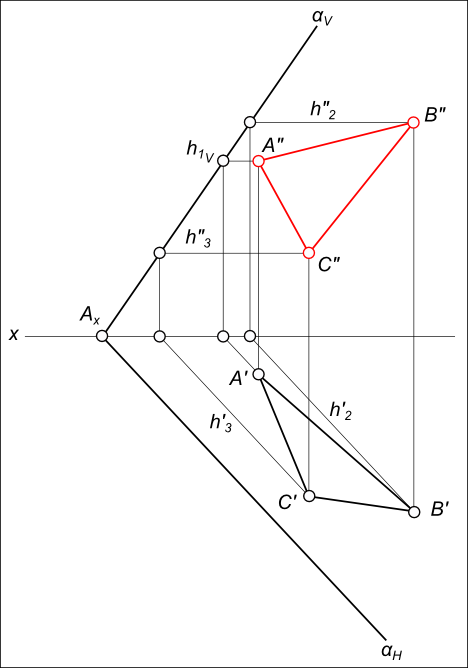
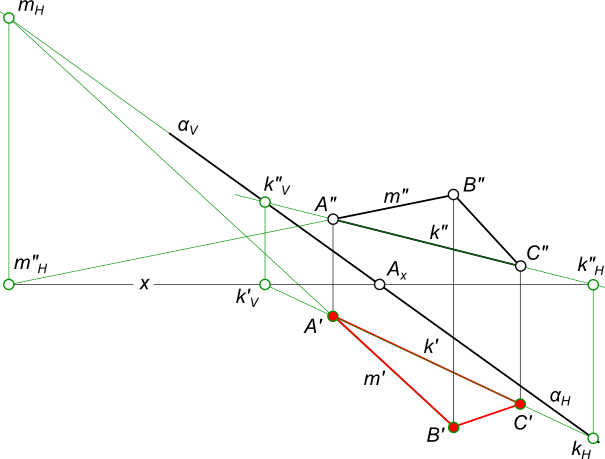
Задача № 1. Эпюра плоскости α задана следами αH и αV. Треугольник ∆ABC, лежащий в плоскости α, задан проекцией ∆A`B`C`. Построить недостающую проекцию треугольника ∆A”B”C”, используя главные линии плоскости
HTML код таблицы, примеры
| Выполняемое действие | Задаваемое положение | Достигнутая цель |
| A ∈ h1 ∧ h1 ∈ α | h`1 ║ αH ⇒ h”1 ║ оси x | h”1 ∩ A`AxA” = A” |
| B ∈ h2 ∧ h2 ∈ α | h`2 ║ αH ⇒ h”2 ║ оси x | h”2 ∩ B`BxB” = B” |
| C ∈ h3 ∧ h3 ∈ α | h`3 ║ αH ⇒ h”3 ║ оси x | h”3 ∩ C`CxC” = C” |
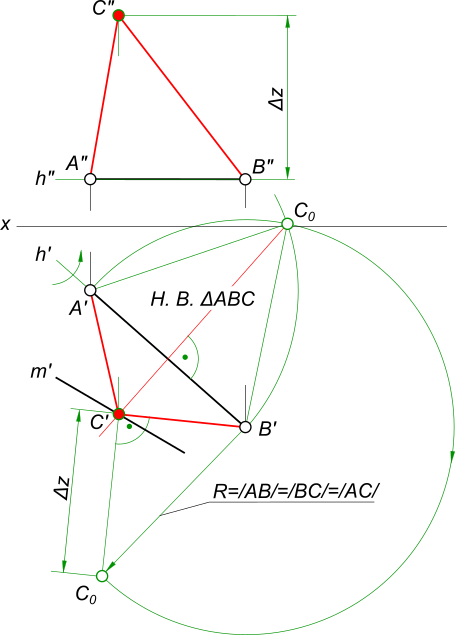
Задача № 2. На построение эпюра плоскости равностороннего треугольника ABC,
Задача № 3. Эпюра плоскости α задана следами αH и αV. Треугольник ∆ABC, лежащий в плоскости α, задан проекцией ∆A”B”C”. Построить недостающую проекцию треугольника ∆A`B`C`, используя прямые общего положения в плоскости
Плоскость на эпюре Монжа в начертательной геометрии с примерами
Плоскость на эпюре Монжа:
Плоскость на эпюре может быть задана шестью способами: тремя точками, не лежащих на одной прямой; прямой и точкой, не лежащей на прямой; двумя параллельными прямыми; двумя пересекающимися прямыми; любой плоской фигурой и следами (рисунок 3.1).
Плоскости аналогично прямым делятся на плоскости общего и частного положения. На рисунке 3.2 представлены пространственные чертежи плоскостей.
У проецирующих плоскостей два следа всегда перпендикулярны осям. Третий след наклонен к соответствующей оси и называется собирательным следом. Он называется так потому, что, если в плоскости находится какой-либо геометрический объект (точка, прямая или кривая линия, треугольник и т.д.), то он проецируется на этот след в линию, совпадающую со следом (след “собирает” на себя проекцию объекта).
У плоскостей, параллельных плоскостям проекций, один след отсутствует, а два других следа являются продолжением друг друга и параллельны соответствующим осям проекций.
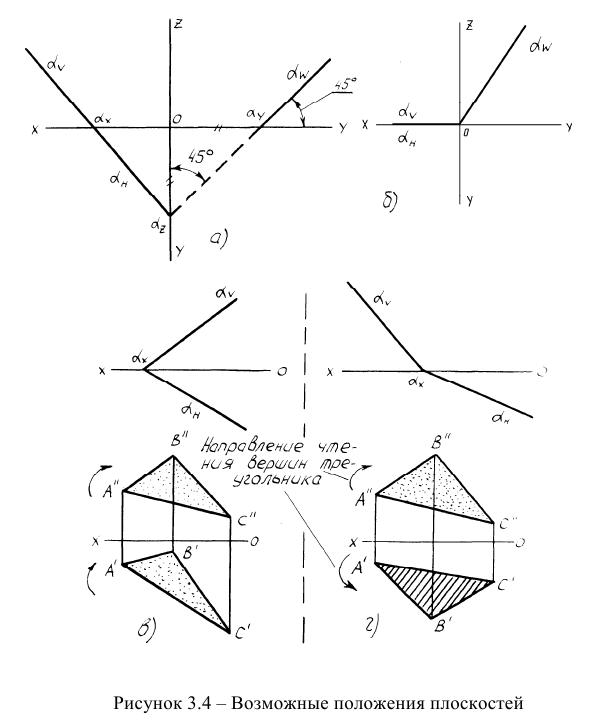
Если плоскость в пространстве равнонаклонена к какой-либо паре плоскостей проекций, то следы такой плоскости вырождаются в прямую линию (рисунок 3.4а).
Плоскости, перпендикулярные к одной из плоскостей проекций и проходящие через ось проекций, называются осевыми плоскостями. Два их следа сливаются с соответствующими осями (рисунок 3.46).
Плоскости общего положения дополнительно делятся на плоскости с односторонней (рисунок 3.4в) и двухсторонней (рисунок 3.4г) видимостью. Признаком односторонней видимости является, например, одинаковое направление чтения букв вершин треугольника на проекциях.
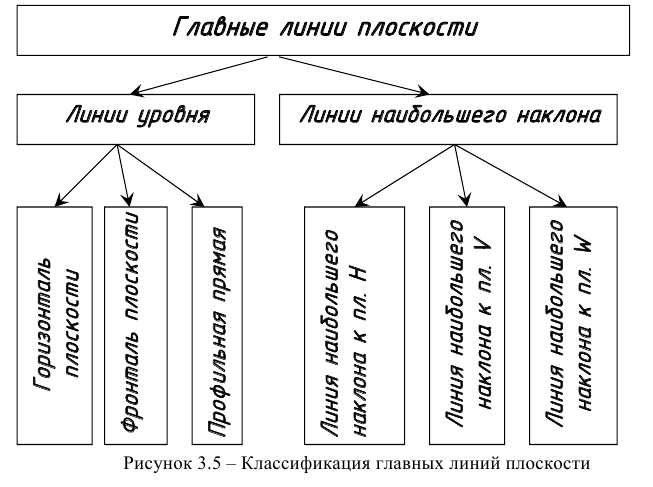
Главные линии плоскости
Главные линии плоскости делятся на линии уровня и линии наибольшего наклона.
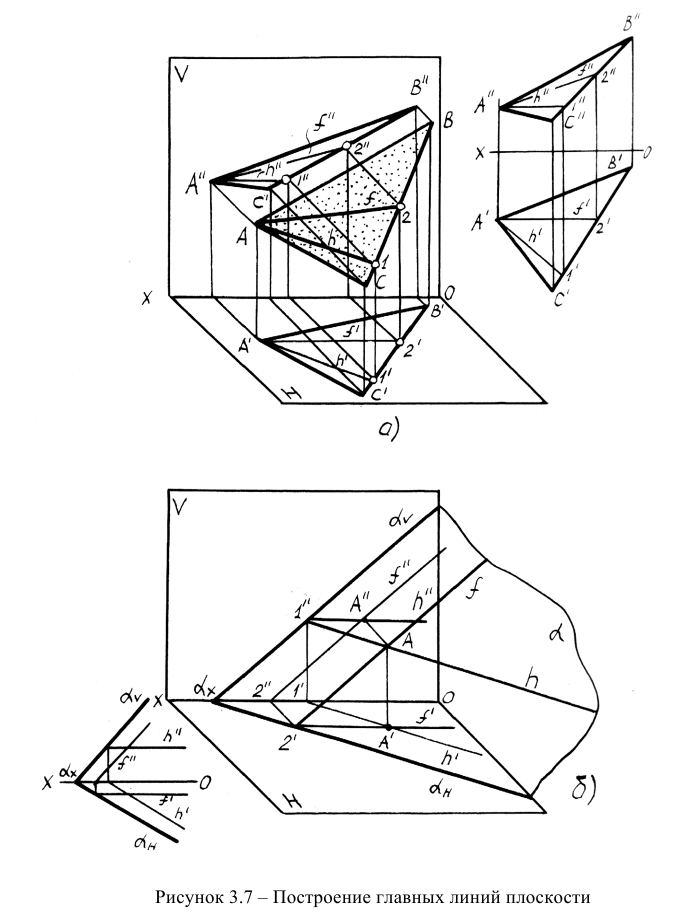
К линиям уровня относятся горизонталь, фронталь и профильная прямая плоскости. Они принадлежат плоскости и проводятся в ней по тем же правилам, что и обычные прямые. В каждой плоскости можно провести бесчисленное множество линий уровня. На рисунке 3.7 показано проведение горизонтали и фронтали в плоскостях, заданных плоской фигурой и следами.
При проведении горизонтали и фронтали в плоскости, заданной треугольником, целесообразно взять одну из вершин треугольника за точку, принадлежащую плоскости, и строить проекции h и f из этой вершины, что упрощает построения.
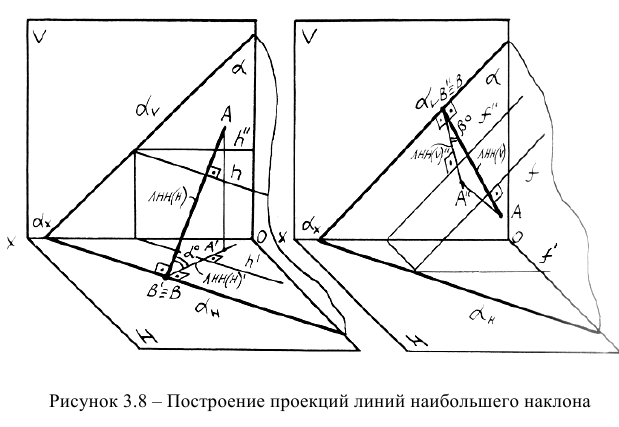
Линия наибольшего наклона плоскости к плоскости проекций Н проводится перпендикулярно к горизонтальному следу плоскости или к горизонтали плоскости. Линия наибольшего наклона плоскости к плоскости проекций V проводится перпендикулярно к фронтальному следу плоскости или к фронтали (рисунок 3.8).
Принцип методики построения проекций ЛНН основывается на теореме прямого угла: если один из катетов прямого угла параллелен какой-либо плоскости, то на эту плоскость прямой угол проецируется в натуральную величину (см. рисунок 2.8).
Проекции 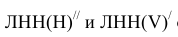
Угол наклона плоскости к плоскости проекций Н (угол 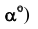
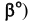
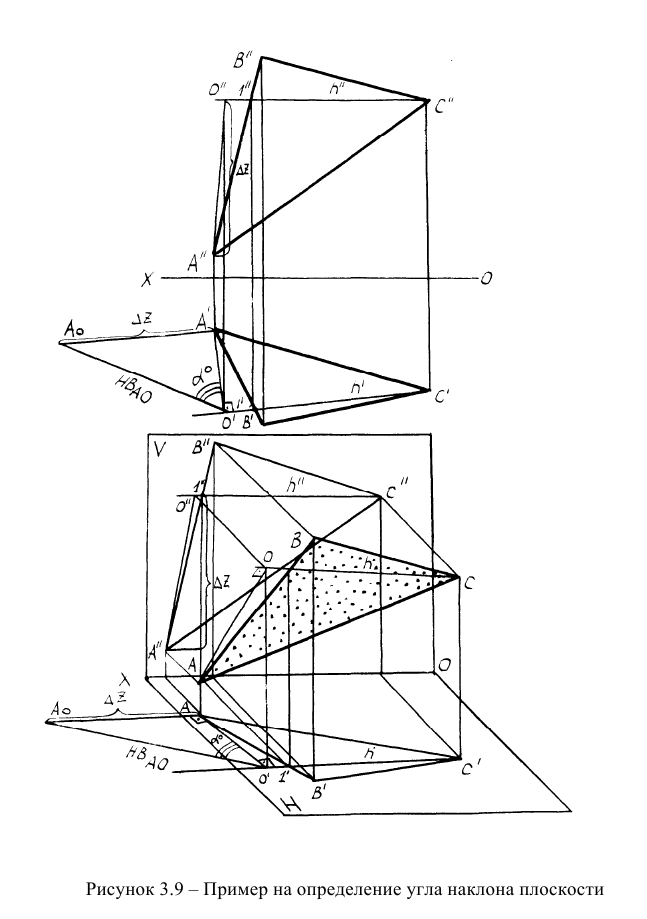
Пример: Определить угол наклона плоскости ЛВС к плоскости проекций Н (рисунок 3.9).
Решение: Для определения угла 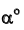
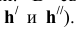
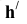
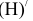
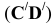
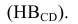
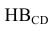
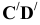
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Лекция 3. Плоскость
3.1. Способы задания плоскости на ортогональных чертежах
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
Рисунок 3.6 – Принадлежность прямой плоскости
\left.\begin
Упражнение
Рисунок 3.7 – Решение задачи
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
\alpha=m\cap n\\\left.\begin
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Упражнение
Алгоритм решения задачи :
\left.\begin
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи :
\left.\begin
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.