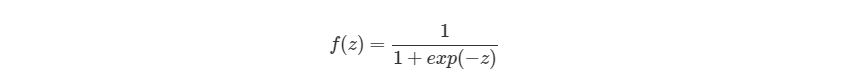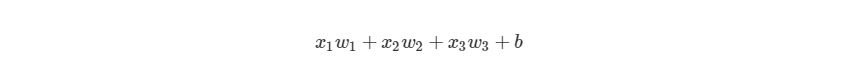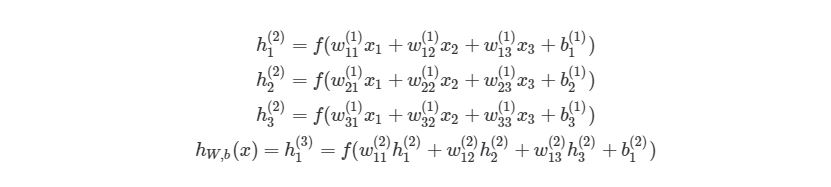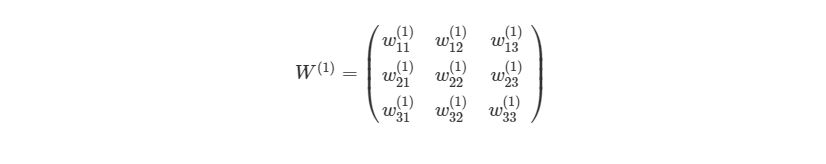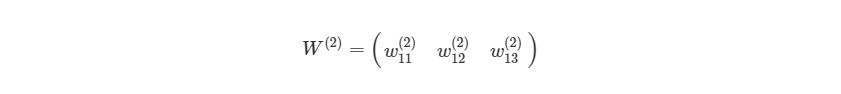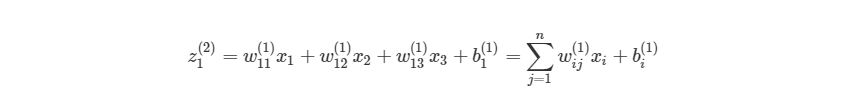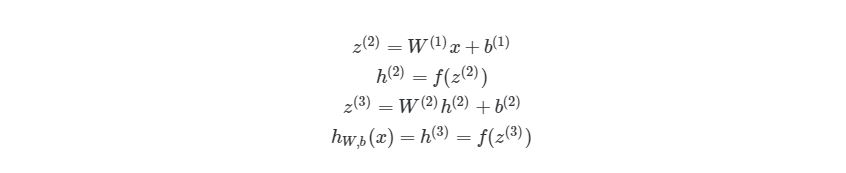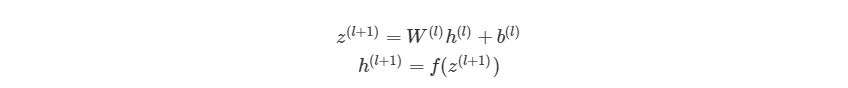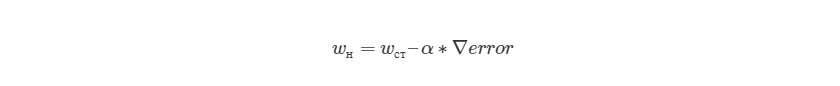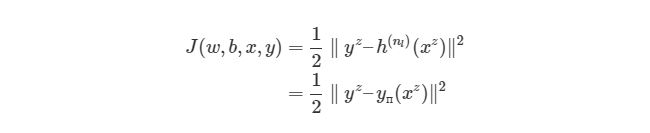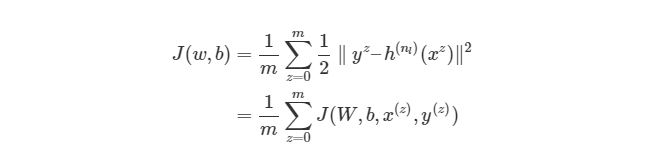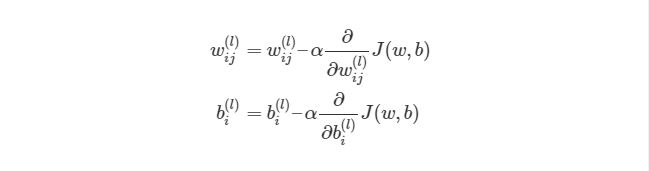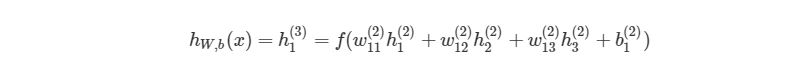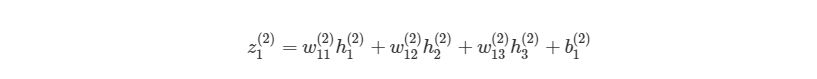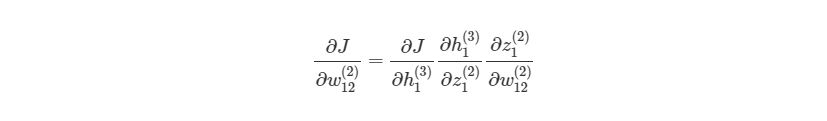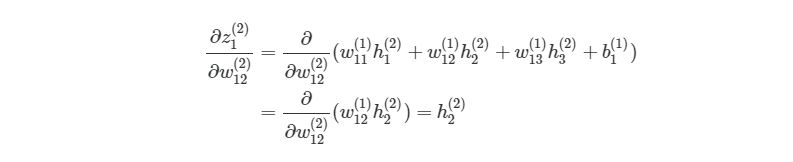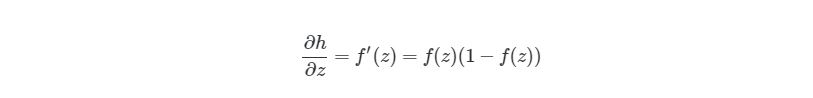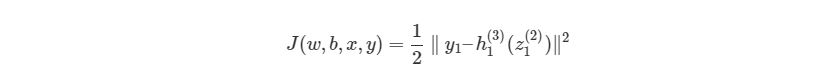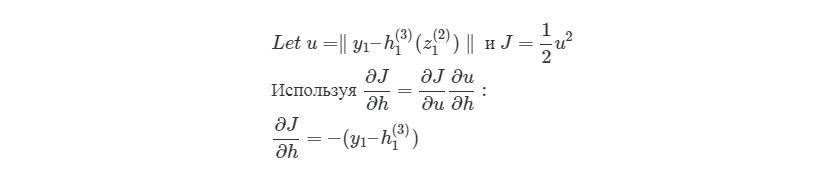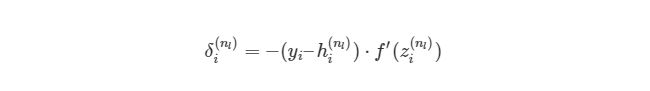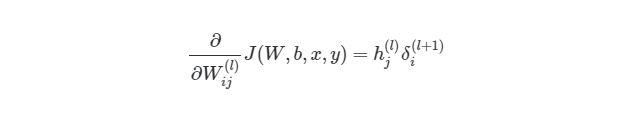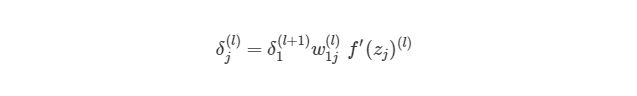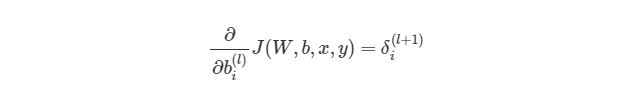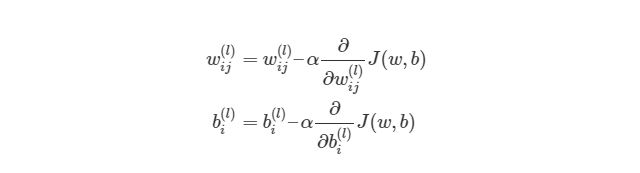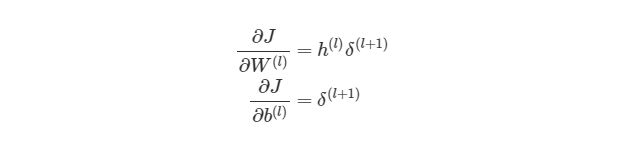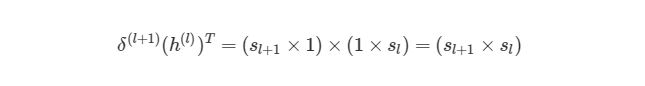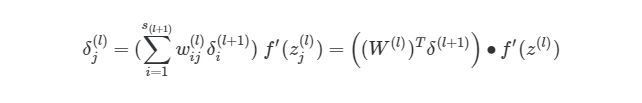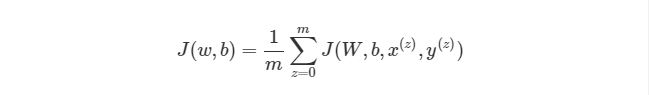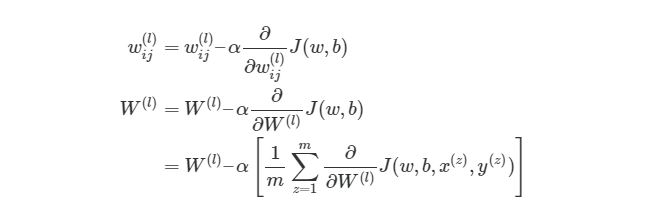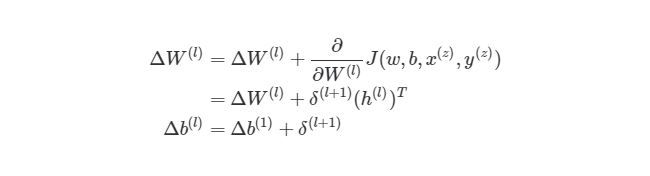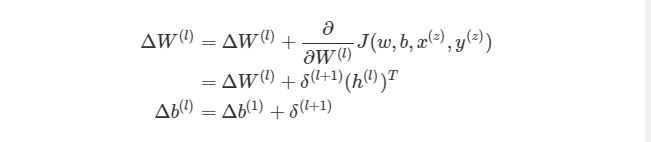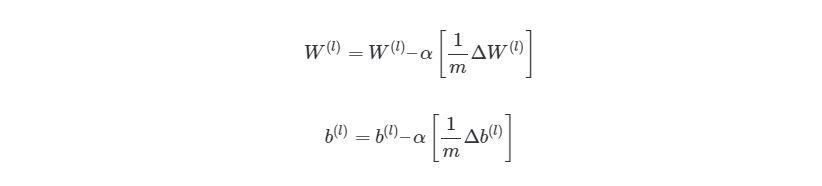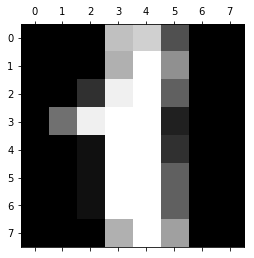на каком языке программирования пишут нейросети

Топ-10 фреймворков для искусственного интеллекта: часть первая

Материал подготовили эксперты компании Hey Machine Learning.

Машинное обучение и искусственный интеллект определённо являются технологическим прорывом. Приложения для подстановки лиц и их состаривания. Голосовые помощники, способные забронировать столик или заказать билет.

Решения, распознающие мерцательную аритмию и сердечный приступ. И это лишь то, что произошло буквально недавно. Популярность ИИ-технологий растёт, а значит, растёт и спрос на них. Это приводит к увеличению всего сообщества разработчиков и к появлению фреймворков ИИ, упрощающих обучение и работу.

Давайте разберёмся, что такое фреймворк. Фреймворк — это набор инструментов и стандартных реализаций для обеспечения более быстрой разработки какого-либо программного продукта. Его часто путают с библиотекой, которая же, в свою очередь, является набором стандартных реализаций, функций и структур данных, облегчающих решение какой-либо задачи.

Если перейти во вселенную метафор, то фреймворк — это как мастерская, в которой вы можете сесть и, например, собрать автомобиль или стул. Тогда с этой точки зрения библиотека — молоток.

Мы в Hey Machine Learning работаем с ИИ-фреймворками ежедневно, поэтому решили написать для вас статью о десяти самых известных из них. На основе собственного использования выделили их положительные и отрицательные стороны, а также добавили информацию о самом эффективном их применении. В первую часть обзора вошли Tensorflow, PyTorch, Keras, Darknet и XGBoost.

TensorFlow — это комплексная платформа для машинного обучения с открытым исходным кодом. Она была разработана командой Google Brain как продолжение закрытой системы машинного обучения DistBelief, однако в ноябре 2015 года компания передумала и открыла фреймворк для свободного доступа.

Как и большинство фреймворков глубокого обучения, TensorFlow имеет API на Python поверх механизма C и C ++, что ускоряет его работу.

TensorFlow имеет гибкую экосистему инструментов, библиотек и ресурсов сообщества. Это позволяет исследователям использовать самые современные МО-технологии, а разработчикам — создавать и развёртывать приложения на базе машинного обучения.

Платформа предоставляет интуитивно понятные высокоуровневые API-интерфейсы, например Keras, с быстрым выполнением, что обеспечивает немедленную итерацию модели и простую отладку. За счёт мультиплатформенности решение позволяет обучать и разворачивать модели в облаке и локально, независимо от используемого пользователем языка.

Если вам необходимо запустить модель машинного обучения на смартфоне или IoT-устройстве, то вам пригодится среда глубокого обучения с открытым исходным кодом TensorFlow Lite. Когда нужно создать и обучить МО-модель на JavaScript, а после развернуть её в браузере или на Node.js, то можно воспользоваться библиотекой TensorFlow.js.

Стоит отметить, что фреймворк постоянно развивается за счёт открытого исходного кода и огромного сообщества энтузиастов. Также за счёт его популярности есть множество уже решённых задач, что существенно упрощает жизнь новоиспечённым разработчикам.

Однако фреймворк не лишён недостатков. Компания Google известна своей любовью к созданию собственных стандартов, что коснулось и фреймворка. Например, если во время работы с TensorFlow в коде вылетает ошибка, то фреймворк не покажет пользователю конкретную строчку, спровоцировавшую её.

Почему так? Это связано с особенностью API TensorFlow, где все операции выполняются через класс tf.Session. В программировании есть две основные парадигмы — императивная и декларативная. В TensorFlow используется второй подход.

Рассмотрим очень грубый пример:

Если думаете, что c = 6, то спешу вас огорчить. На самом деле оно равно:

Это значит, что из-за декларативного подхода, вы не умножаете 2 * 3, а объявляете операцию, которая умножает 2 * 3.

Чтоб получить 6, необходимо выполнить операцию умножения чисел через сессию:

Теперь рассмотрим пример посложнее: сделаем вход не константным и будем использовать поэлементное умножение матриц.

Возьмём матрицы разных размеров, что должно привести к ошибке, потому что нельзя поэлементно умножить две матрицы разной формы.

Теперь даём на вход вектор из двух элементов и из трёх.

Ничего непонятно, но очень интересно.

Всё потому, что ошибка — внутри сессии.

Конечно, есть способы обезопасить себя от подобного, однако, например, в PyTorch такое вообще не возможно.

Ещё одна проблема TensorFlow, которую следует выделить, — фреймворк всегда забирает всю видеопамять. Если вы хотите его ограничить, то необходимо создавать файл конфигурации и явно указывать, что можно брать. Также фреймворк можно ограничить напрямую, например, позволить взять не больше 50% видеопамяти.

Из-за подобного поведения с памятью могут возникнуть проблемы в работе. Предположим, что в одном проекте множество различных моделей, одни из которых написаны на PyTorch, а другие — на TensorFlow. Если изначально мы создадим TensorFlow-модель и не ограничим её, то она использует всю видеопамять при том, что ей необходимо всего 0,5 ГБ, и в итоге на PyTorch-модели попросту не хватит места.

Проекты, которые используют фреймворк TensorFlow:

PyTorch — это среда машинного обучения на языке Python с открытым исходным кодом, обеспечивающая тензорные вычисления с GPU-ускорением. Она была разработана компанией Facebook и представлена в октябре 2016 года, а открыта для сторонних разработчиков — в январе 2017 года. Фреймворк подходит для быстрого прототипирования в исследованиях, а также для любителей и небольших проектов.

Фреймворк предлагает динамические графы вычислений, которые позволяют обрабатывать ввод и вывод переменной длины, что полезно, например, при работе с рекуррентными нейронными сетями. Если коротко, то за счёт этого инженеры и исследователи могут менять поведение сети «налету».

За счёт глубокой интеграции фреймворка с кодом C++ разработчики могут программировать на C и C++ с помощью API-расширения на основе FFI для Python.

В отличие от TensorFlow, PyTorch менее гибок в поддержке различных платформ. Также в нём нет родных инструментов для визуализации данных, но есть сторонний аналог, называемый tensorboardX.

Однако, снова же, в отличие от TensorFlow, если при работе с PyTorch вылетает ошибка, то это конкретная недоработка в коде и система выделит вам именно ту строчку, которая её спровоцировала.

Также при развёртке сетей на GPU PyTorch самостоятельно займёт только необходимую видеопамять.

Проекты, которые используют фреймворк PyTorch:

Keras — открытая среда глубокого обучения, написанная на Python. Она была разработана инженером из Google Франсуа Шолле и представлена в марте 2015 года.

Фреймворк нацелен на оперативную работу с нейросетями и является компактным, модульным и расширяемым. Подходит для небольших проектов, так как создать что-то масштабное на нём сложно и он явно будет проигрывать в производительности нейросетей тому же TensorFlow.

Keras работает поверх TensorFlow, CNTK и Theano и предоставляет интуитивно понятный API, который, по мнению наших инженеров, пока что является лучшим в своём роде.

Фреймворк содержит многочисленные реализации широко применяемых строительных блоков нейронных сетей, таких как слои, целевые и передаточные функции, оптимизаторы, а также множество инструментов для упрощения работы с изображениями и текстом.

Deeplearning4j использует Keras в качестве своего Python API и позволяет импортировать модели из Keras, а также через Keras из Theano и TensorFlow.

Проекты, которые используют фреймворк Keras:

Darknet — это фреймворк с открытым исходным кодом, написанный на языке C с использованием программно-аппаратной архитектуры параллельных вычислений CUDA. Он быстрый, лёгкий и удобный в использовании. Также Darknet поддерживает вычисления на базе CPU и GPU.

Обученные веса Darknet хранит в формате, который может быть распознан с помощью разных методов на различных платформах. Однако это может стать проблемой, если вы решите натренировать модель на одном сверхмощном оборудовании, а затем использовать её на другом.

Так как фреймворк написан на C и не имеет другого API, то в случае, когда требования платформы или собственные предпочтения заставят обратиться к другому языку программирования, вам придётся дополнительно заморочиться над его интеграцией. К тому же он распространяется только в формате исходного кода, и процесс компиляции на некоторых платформах может быть несколько проблематичным.

Фреймворк не рекомендуется использовать для сложных проектов, разве что вам необходимо создать сверхбыстрый детектор объектов.

Проекты, которые используют фреймворк Darknet:

XGBoost — это фреймворк с открытым исходным кодом, который предлагает систему градиентного бустинга для C++, Java, Python, R, Julia. Он разработан для обеспечения высокой эффективности, гибкости и портативности.

Этот фреймворк относится не к глубокому обучению, как все вышепредставленные, а к классическому.

Изначально это был исследовательский проект Тяньцзи Чена и Карлоса Гестрина в составе Distributed [Deep] Machine Learning Community, но позже он был расширен и представлен публике на конференции SIGKDD в 2016 году, где произвёл фурор.

После своей презентации фреймворк лидировал в соревнованиях Kaggle и до сих пор остаётся фаворитом для решения большинства задач на платформе.

XGBoost фокусируется на скорости вычислений и производительности модели и подходит для решения задач регрессии, классификации и упорядочивания. Если данные можно представить в виде таблицы, то точность и производительность будут существенно выше, чем у DeepLearning-решений. Любимый инструмент Data Scientist-ов.

Фреймворк совместим с операционными системами Windows, Linux и OS X, а также поддерживает кластеры AWS, Azure и Yarn, хорошо работает с Flink, Spark.

Так всё же, какой фреймворк к какой задаче лучше всего применить?

TensorFlow хорош для продвинутых проектов, таких как создание многослойных нейронных сетей. Может использоваться для распознавания речи, лиц, объектов и изображений, а также для работы с текстом.

PyTorch подойдёт в случае, когда вам необходимо обучить модели быстро и эффективно. Удобный для быстрого прототипирования в исследованиях, а также для любителей и небольших проектов.

Keras подходит для быстрого прототипирования. Хорош в кейсах, связанных с переводом, распознаванием изображений и речи.

Darknet подходит для небольших проектов. Хорошо работает в задачах обнаружения.

XGBoost может использоваться для решения задач регрессии, классификации, упорядочивания и пользовательских задач на предсказание.

Мы надеемся, что наша статья о топ-10 фреймворках для искусственного интеллекта расскажет вам что-то новое и полезное, а также поможет подобрать наиболее подходящее решение для вашего проекта.

Поверхностно, keras это надстройка над tf. А не отдельный фреймворк. Это как jquery для js.

только js это не фреймворк

Полностью согласен. Тока хотел тоже самое написать:)

Теоретически вы правы, однако на практике дела обстоят немного иначе.

Термин «фреймворк» является достаточно расплывчатым и может означать много разных вещей в зависимости от контекста. Фреймворком может называться всё, что используется при разработке приложений: библиотека, набор из множества библиотек, набор сценариев или любое программное обеспечение, необходимое для создания приложения.

Keras действительно является надстройкой и, кстати, не толькоTensorFlow, но и CNTK и Theano. Он может считаться фреймворком, так как используется для создания полноценных решений типа Mask R-CNN и face_classification.

Также, когда дело касается решения задач распознавания изображений и машинного перевода, Keras всегда рассматривают как альтернативу TensorFlow и PyTorch, так как он удобен в использовании, лёгок в освоении и имеет хорошую документацию.

Источник

Digitrode

цифровая электроника вычислительная техника встраиваемые системы

Языки программирования для искусственного интеллекта

Рейтинг языков программирования для ИИ и машинного обучения

Искусственный интеллект (ИИ) – это широкое и растущее технологическое поле, и это означает, что ИИ может быть реализован на разных языках программирования. Однако по-прежнему трудно определить, какой из многих языков следует использовать для разработки ИИ. Поэтому в данном материале мы приведем некоторые из лучших языков программирования ИИ, которые помогут вам реализовать его.

Julia

Julia – это высокоуровневый язык программирования общего назначения, разработанный Джеффом Безансоном, Стефаном Карпински, Вирал Б. Шахом и Аланом Эдельманом в 2009 году. Он разработан с нацеленностью на высокопроизводительный численный анализ и вычислительную науку, поэтому он не включает необходимость отдельной компиляции по скорости. Простой синтаксис и глубокие математические корни делают Julia дружественным языком программирования для аналитиков данных. Он также включает Flux, основу для машинного обучения и ИИ. В сочетании с математическим синтаксисом Julia предлагает идеальный способ выражения алгоритмов. Julia также поддерживает другие платформы машинного обучения, такие как TensorFlow и MXNet.

Haskell

Haskell – стандартизированный, универсальный язык программирования, разработанный с нестрогой семантикой и сильной статической типизацией. Первоначально разработанный в 1990 году, Haskell в основном используется в академических кругах, хотя есть и некоторые примеры его использования в промышленности и коммерции для проектов в AT&T, Facebook, Google и других. Haskell основан на семантике языка программирования Miranda и позволяет эффективным библиотекам реализовывать алгоритмы ИИ.

В отличие от других, R – уникальный язык программирования, а также бесплатная программная среда с открытым исходным кодом для статистических вычислений и графики. Разработанный в 1993 году Росом Ихакой и Робертом Джентльменом, R широко используется среди аналитиков данных для разработки статистического программного обеспечения и анализа данных. Он также используется в искусственном интеллекте нового стиля и общем машинном обучении. R предоставляет несколько парадигм программирования, таких как векторное вычисление, функциональное программирование и объектно-ориентированное программирование и рассматривается как один из основных стандартных языков для таких областей, как финансы, биология и медицина.

C++ был разработан с учетом производительности, эффективности и гибкости, что делает его идеальным выбором для многих проектов программирования ИИ, которым необходима скорость. По сравнению с другими языками программирования, C++ имеет более быстрое выполнение и более низкую задержку, что делает его полезным для поиска решений сложных проблем ИИ. Он также позволяет широко использовать алгоритмы и является эффективным средством написания статистических методов ИИ, таких как нейронные сети.

MATLAB

MATLAB (Matrix Laboratory) является патентованным языком программирования, разработанным MathWorks. Он широко используется многими разработчиками программного обеспечения и разработчиками для анализа краевых систем и проектов ИИ. Это простой в использовании язык со встроенной графикой, которая позволяет разработчикам визуализировать данные и получать от них значимую информацию. MATLAB – хороший выбор для машинного обучения и проектов ИИ при задачах визуализации и выполнения матриц.

Python

Python – широко применяемый язык программирования и может быть использован для реализации ИИ из-за простой и бесшовной структуры, которую он предлагает. Синтаксис Python позволяет легко реализовать различные алгоритмы ИИ, что также позволяет сократить время разработки по сравнению с другими доступными языками программирования. Применение Python позволяет пользователям создавать нейронные сети с набором полезных библиотек, которые могут использоваться для разработки ИИ. Другие функции включают возможность тестирования алгоритмов без необходимости их реализации. Он также поддерживает объектно-ориентированные, функциональные и процедурно-ориентированные стили программирования.

Lisp является одним из самых старых доступных языков программирования, но все же остается одним из предпочтительных вариантов разработки ИИ из-за его уникальных функций. Это, по сути, практическая математическая нотация для компьютерных программ. Разработчики склонны идти на Lisp в машинном обучении его гибкости приспосабливаться к проблеме, которая нуждается в решении. Помимо этого, Lisp также предлагает быстрые возможности прототипирования, библиотеку типов коллекций, поддержку символических выражений и другое.

Java, чрезвычайно популярный язык программирования, также может рассматриваться как хороший выбор для программирования ИИ, поскольку он обеспечивает алгоритмы поиска и нейронные сети. Это простой для понимания язык, который предлагает графическое представление, отладку и масштабируемость. Его портативность делает его предпочтительной реализацией для различных приложений на основе наличия различных встроенных типов.

Источник

Пишем свою нейросеть: пошаговое руководство

Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.

В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.

1 Что такое искусственная нейросеть?

Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.

2 Структура ИНС

2.1 Искусственный нейрон

Которая выглядит следующим образом:

2.2 Узлы

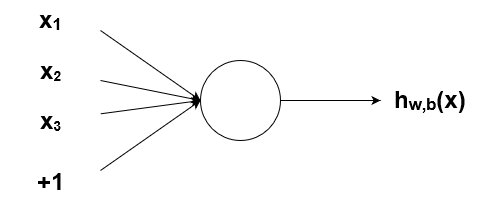
Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.

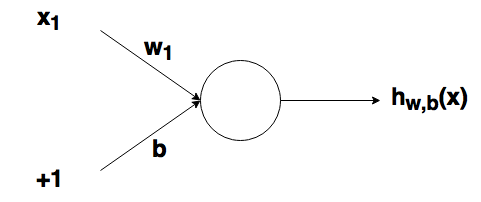
Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.

Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:

где w_i— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.

2.3 Смещение

Рассмотрим простой узел, в котором есть по одному входу и выходу:

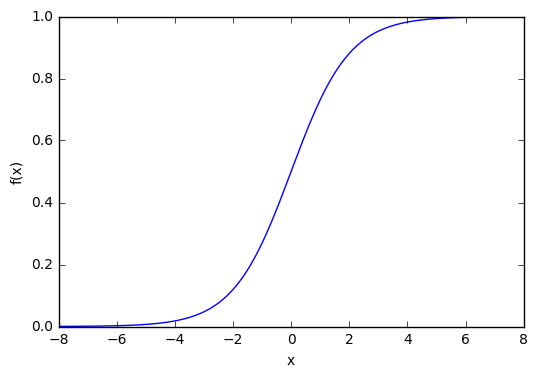
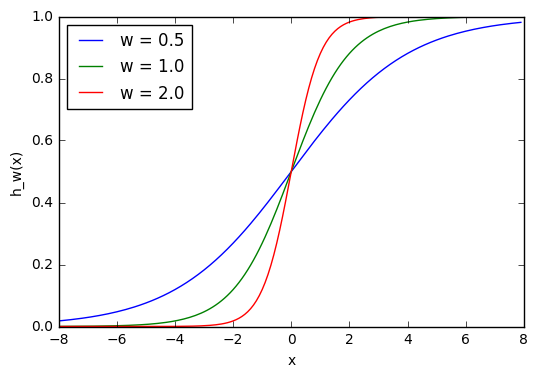
Ввод для активационной функции в этом узле просто x₁w₁. На что влияет изменение в w₁ в этой простой сети?

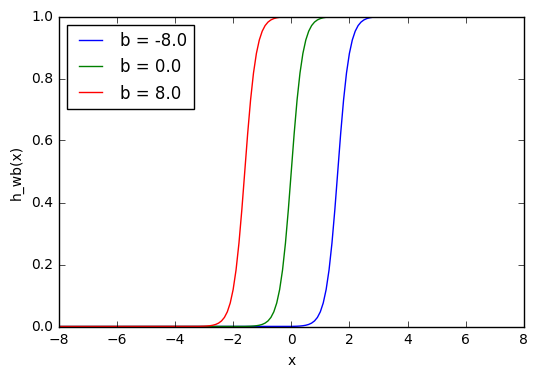
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:

Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.

2.4 Составленная структура

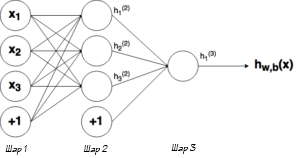
Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:

2.5 Обозначение

3 Процесс прямого распространения

Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:

3.1 Пример прямого распространения

Представим эту матрицу через массивы библиотеки numpy.

Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:

Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:

Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:

3.2 Первая попытка реализовать процесс прямого распространения

Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.

Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:

возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:

3.3 Более эффективная реализация

В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.

3.4 Векторизация в нейронных сетях

, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:

Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:

3.5 Умножение матриц

Распишем z (l+1) =W (l) h (l) +b (l) на выражение из матрицы и векторов входного слоя ( h (l) =x):

Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.

Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:

Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.

Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.

На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.

4 Градиентный спуск и оптимизация

Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L 1 (Это будет рассмотрено позже).

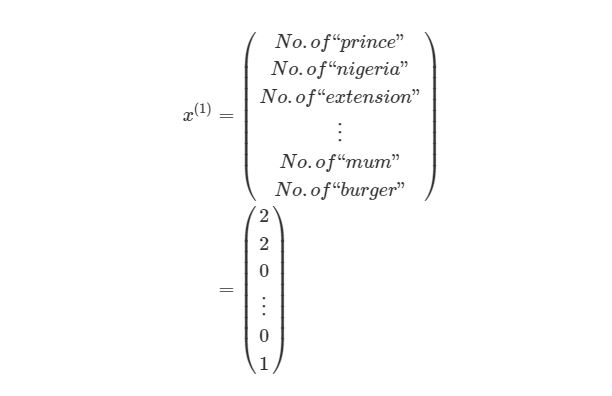
y (1) в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0. 0)для буквы а, (0,1. 0) для буквы б и т. д.

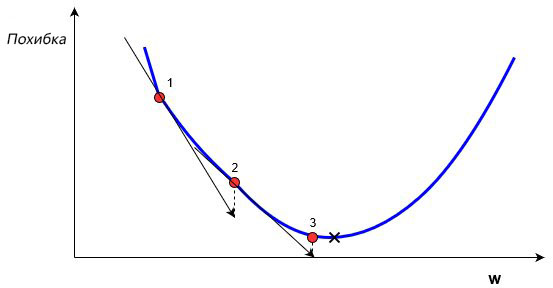
В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:

На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.

Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:

, где w_н означает новое значение w, w_ст— текущее или «старое» значение w, ∇error является градиентом погрешности на w_ст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.

4.1 Простой пример на коде

Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.

4.2 Функция оценки

Выражение является функцией оценки учебного экземпляра z_th, где h (nl) является выходом последнего слоя, то есть выход нейронной сети. h (nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L 2 погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(x z )-y z ), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.

Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:

Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.

4.3 Градиентный спуск в нейронных сетях

Градиентный спуск для каждого веса w_(ij) (l) и смещение bi(l) в нейронной сети выглядит следующим образом:

Значения ∂/∂w_ij (l) и ∂/∂b_i (l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.

4.4 Пример двумерного градиентного спуска

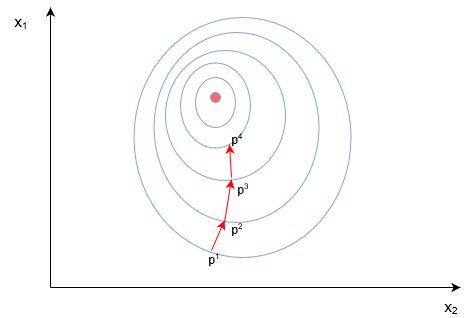
Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:

Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x₁ в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).

Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.

4.5 Углубляемся в обратное распространение

Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.

Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:

Выход этой нейронной сети находится по формуле:

Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z₁ (2) /∂w₁₂ (2) :

здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:

Мы выяснили, как находить ∂J/∂w₁₂ (2) по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:

, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:

, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.

4.6 Распространение в скрытых слоях

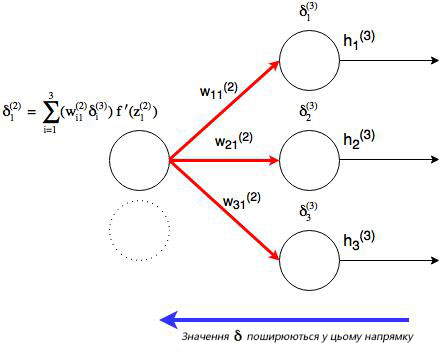
Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(y_i-h_i (nl) )имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.

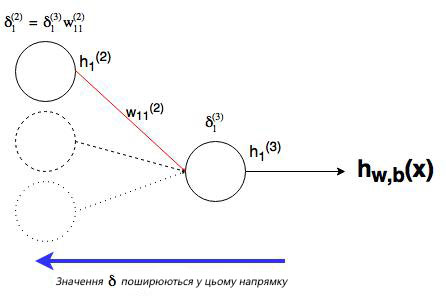
Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:

, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δ_j (l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:

Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:

Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.

4.7 Векторизация обратного распространения

Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):

Используя операцию трансформирования, мы можем достичь результата, который нам нужен.

Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:

символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W (l) ) T δ_(l+1))требует еще одного сложения весов и значений δ.

4.8 Реализация этапа градиентного спуска

Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:

Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):

4.9 Конечный алгоритм градиентного спуска

Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.

Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.

5 Имплементация нейросети языке Python

Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:

01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.

5.1 Масштабирование данных

Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:

Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:

5.2 Создание тестов и учебных наборов данных

Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:

5.3 Настройка выходного слоя

В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:

Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].

5.4 Создаем нейросеть

Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:

Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W (l) Когда итерация (l) б. Найдите значение δ ( nl) выходного слоя. Обновите ΔW (l) и Δb ( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:

Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через <>). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:

Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)

Далее запустим процесс прямого распространения через нейронную сеть:

И наконец, найдем выходной слой δ (nl) и значение δ (l) в скрытых слоях для запуска обратного распространения:

Теперь мы можем соединить все этапы в одну функцию:

И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:

После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.

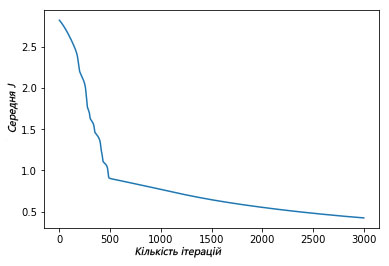
Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:

Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.

5.5 Оценка точности модели

Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:

Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.

Источник