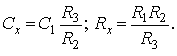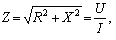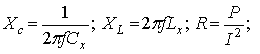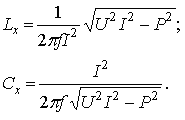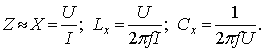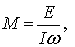Зарегистрирован: Пн: 15 мар 2010 10:48
Сообщения: 85

Вы можете отключить эти сообщения.

_________________
С уважением, Михаил.

_________________
«Сколько можно заниматься полупроводниками?! Пора заняться проводниками в целом. «

_________________
Количество металла в земле обратно пропорционально количеству мужиков, копающих её поверхность.

_________________
«Сколько можно заниматься полупроводниками?! Пора заняться проводниками в целом. «

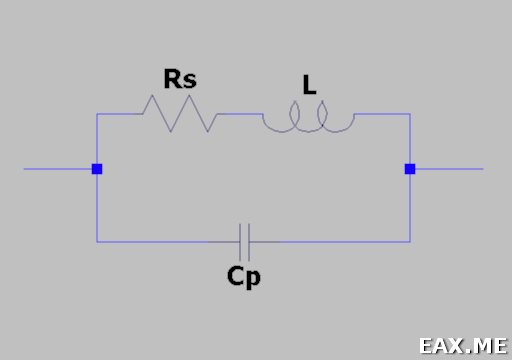
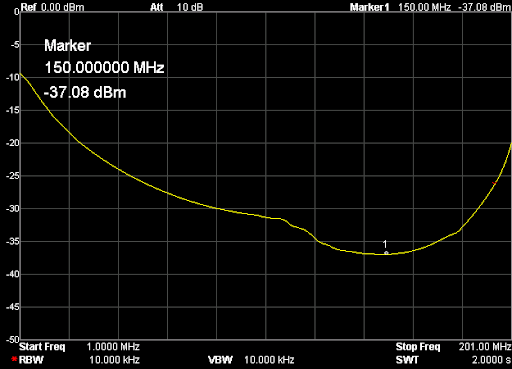
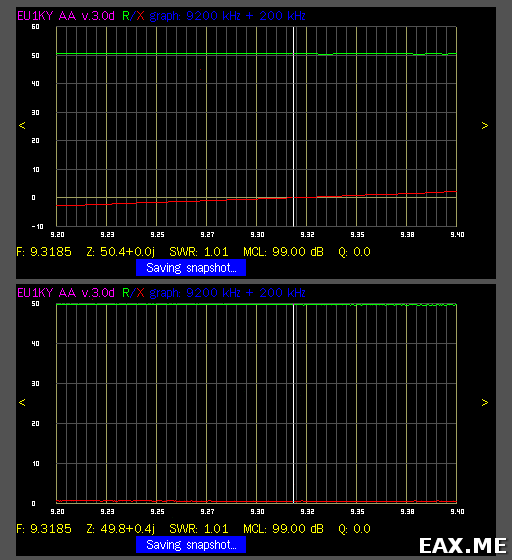
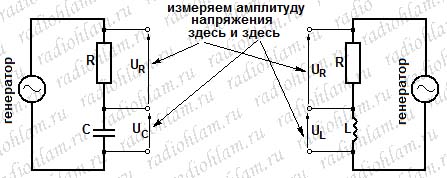
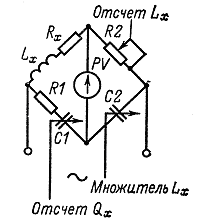
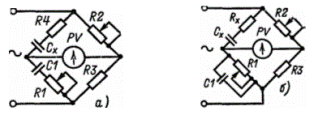
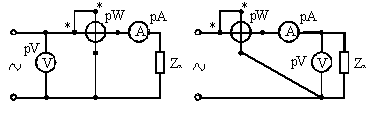
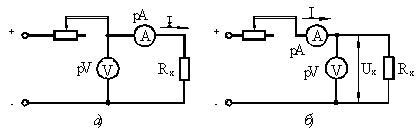
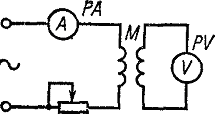
Часовой пояс: UTC + 3 часа

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1

Источник

Блог alex123al97

Измерение индуктивности катушек резонансным методом

Запись опубликована alex123al97 · 17 октября 2017

Суть метода состоит в подборе резонансной частоты для собранного колебательного контура с известной (проверенной) емкостью конденсатора. Резонансная частота засекается любым мультиметром по пику напряжения на контуре. А зная частоту и емкость можно вычислить индуктивность.

В качестве генератора частоты использовал звуковую карточку (ЗК) ПК и скачанную с интернета одну из многочисленных программ – генераторов.

Для примера проведу парочку наглядных измерений.

Опыт №1. Беру известные конденсатор 1,5uF и дроссель ДМ-0,6-50 мкГн. Собираю контур, подключаю блок к ЗК и мультиметру, запускаю генератор и прогоняю частоту в обратном порядке – начиная с 20 кГц в сторону уменьшения. Напряжение сразу начало возрастать и застыло на максимуме в пределах 18,85-18,65 кГц, откуда выбрал среднее значение – 18,75 кГц.

Далее можно проводить расчеты вручную, можно ввести формулу в Excell, можно написать программку, а можно и воспользоваться многочисленными онлайн калькуляторами, что я и сделал, используя первый попавшийся сайт: http://coil32.ru/calc/jslcc.html

Ввожу емкость, частоту и без малого получаю указанную на дросселе индуктивность.

Меряю индуктивность недавно приобретенным тестером LCR-T4 и получаю результат (с учетом разрядности) 240 мкГн.

Как видите, метод немного неудобный, заставляет подстраивать контур под ограниченные пределы частоты, но имеет право на жизнь. Насколько точно он меряет – вопрос философский, поскольку все в этом мире относительно. Лично меня в схемотехнике он не подводил и долгое время устраивал простотой и минимальными требованиями к ресурсной базе и измерительной аппаратуре.

Следует также отметить, что данным методом можно измерять и емкость конденсаторов, используя катушки известной индуктивности.

Источник

Записки программиста

Определяем добротность и частоту собственного резонанса катушки индуктивности

Как ни странно, в катушках индуктивности нас в первую очередь интересует индуктивность. Измерить индуктивность не сложно. Готовые RLC-метры стоят недорого. Если RLC-метра нет, но есть осциллограф, индуктивность можно определить с его помощью. Также нормальный антенный анализатор без труда измеряет как индуктивность, так и емкость. Но у катушек индуктивности есть еще по крайней мере два важных свойства — частота собственного резонанса и добротность. Давайте разберемся, почему эти свойства важны и как их измерить.

Суть проблемы

Катушки индуктивности, существующие в реальном мире, можно описать при помощи следующей модели:

Здесь L — это индуктивность катушки. Катушка мотается неким проводником, а реальный проводник имеет отличные от нуля потери. Резистор Rs (он же ESR, equivalent series resistance) как раз отображает эти потери. Конденсатор Cp — это паразитная емкость между витками катушки.

Можно заметить, что индуктивность L и конденсатор Cp образуют параллельный колебательный контур. У этого контура есть резонансная частота. Она и называется частотой собственного резонанса катушки (self-resonant frequency). Ниже этой частоты катушка ведет себя, как катушка. Однако выше она начинает вести себя больше как конденсатор. Определив частоту собственного резонанса, мы поймем, на каких частотах может быть использована катушка.

Rs имеет сложную природу, и работать с ним напрямую неудобно. Поэтому вместо того, чтобы говорить об Rs, говорят о добротности (quality factor или Q). Добротность — это безразмерная величина, характеризующая скорость затухания колебаний в колебательной системе. Чем больше Q, тем меньше затухания.

Для катушек индуктивности добротность определяется, как отношение реактивного сопротивления к Rs:

Реактивное сопротивление является функцией от частоты. Rs на самом деле тоже зависит от частоты. В мире любительского радио обычно говорят о Q на рабочих частотах катушки. Предполагается, что на этом интервале частот добротность меняется незначительно.

Стоит упомянуть, что различают холостую добротность (unloaded Q) и нагруженную добротность (loaded Q). В рамках этой статьи под добротностью понимается исключительно холостая добротность. Нагруженная добротность возникает, когда катушку помещают в конкретную электрическую цепь.

Испытуемый

Попробуем определить частоту собственного резонанса и добротность такой катушки:

Катушка намотана проводом МГТФ площадью сечения 0.35 кв.мм на трубе ПВХ с внешним диаметром 25 мм. Для принудительного шага я мотал два параллельных провода. Затем один провод постепенно отматывался, а второй фиксировался лаком. Длина намотки составила 30 мм, индуктивность — 2 мкГн.

Такой способ намотки был использован с целью получить не самую позорную добротность. За годы экспериментов радиолюбители выработали хорошие практики, позволяющие максимизировать добротность. Основные рекомендации:

Кое-какие подробности можно найти в 9-ой главе книги ON4UN’s Low Band DXing, 5th Edition, в разделе 3.7.2 Making or Buying High-Q Loading Coils. Отмечу, что просто следовать этим советам недостаточно. Если ваша задача — получить как можно большую добротность, нужно брать конкретные доступные материалы, мотать катушки и измерять.

На самом деле, мной было намотано пять катушек пятью разными способами. Приведенная выше имела максимальную добротность.

Ищем собственный резонанс

Для определения частоты собственного резонанса было решено воспользоваться анализатором спектра. С тем же успехом подойдет осциллограф с генератором сигналов, или RTL-SDR с генератором шума. Но анализатор спектра удобнее.

Для подключения катушки между следящим генератором и входом анализатора было использовано такое приспособление:

Экраны BNC-разъемов соединены между собой, а жилы идут к «банановым» коннекторам. К этим коннекторам и подключается катушка.

В итоге получаем такую АЧХ:

Перед нами частоты от 1 до 201 МГц, цена деления по горизонтали — 20 МГц. Собственный резонанс, если верить графику, пришелся где-то на 150 МГц. Ниже аттенюация сигнала увеличивается с ростом частоты. Так и должна работать катушка. Выше аттенюация уменьшается с ростом частоты. Это поведение конденсатора.

Какие выводы отсюда можно сделать? Катушку можно использовать на частотах где-то до 37 МГц. На частотах, приближающихся к частоте собственного резонанса, использовать катушки нельзя. Причина заключается в том, что добротность падает по мере приближения к частоте собственного резонанса. На частоте собственного резонанса добротность равна нулю. Рекомендуется использовать катушки на частотах в 4+ раза ниже частоты собственного резонанса.

Определяем добротность

Для определения добротности воспользуемся подходом из статьи Fixture for Measuring Inductor Q with your Antenna Analyzer [PDF], которую написал Phil Salas, AD5X. По инструкции из статьи было изготовлено такое устройство:

Идея довольно простая. Антенный анализатор подключается к BNC разъему, а катушка подключается к «банановым» коннекторам. В первом положении тумблера антенный анализатор измеряет эквивалент нагрузки 50 Ом. Для эквивалента нагрузки было использовано 20 соединенных параллельно резисторов 1 кОм ± 1%. Во втором положении измеряется последовательный колебательный контур, образованный этим же резистором 50 Ом, измеряемой катушкой и КПЕ.

На резонансной частоте последовательный LC-контур представляет собой КЗ, и мы увидим чисто активное сопротивление около 50 Ом:

В данном случае (первый график) резонанс попал на 9.3185 МГц. Антенный анализатор видит 50.4 Ом. Переключаем тумблер в другое положение. Видим сопротивление резистора без контура. Оно составило 49.8 Ом (второй график). Есть также небольшая реактивность в 0.4j. Ею мы пренебрежем, поскольку это всего лишь:

… 6.8 нГн, почти в 300 раз меньше измеряемых 2 мкГн.

Смотрите, что получается. С контуром было 50.4 Ом, а без контура — 49.8 Ом. Разница в 0.6 Ом включает в себя Rs катушки, а также потери на конденсаторе. Но конденсаторы обладают существенно большей добротностью (> 1000), чем катушки. Поэтому разница в 0.6 Ом приходится преимущественно на Rs катушки.

Теперь у нас есть все необходимое для вычисления добротности:

Добротность порядка 200 — это неплохой результат. Обычные покупные катушки для сквозного монтажа имеют добротность в пределах 100. Не удивительно, что бывалые радиолюбители предпочитают мотать катушки самостоятельно. Случайная самодельная катушка из медной проволоки будет иметь добротность уже порядка 100-150. Согласно Low Band DXing, после некоторой практики можно легко делать катушки с добротностью

400. В качестве потолка в различных источниках приводится Q от 800 до 1000.

Домашнее задание: Смотайте катушку с индуктивностью побольше, порядка 70 мкГн. Для такой катушки вам понадобится каркас около 70 мм и 30 витков эмалированной проволоки диаметром 0.9 мм. Каким вышел Rs? Куда попала частота собственного резонанса? Сравните с приведенными выше результатами.

Внимательный читатель может поинтересоваться, а почему номинал резистора был выбран именно 50 Ом? Это сделано лишь по той причине, что ошибка измерения антенного анализатора при таком сопротивлении минимальна. В теории, с тем же успехом можно использовать любое другое сопротивление, лишь бы оно было чисто активным.

Заключение

Допустим, мы спаяли генератор или фильтр, и он работает не так, как ожидалось. Причина может заключаться к собственном резонансе катушек. Слишком большие потери в согласующем устройстве? Причина может быть в низкой добротности компонентов. Теперь мы имеем больше шансов правильно диагностировать такие проблемы, или еще лучше — вообще избегать их.

Источник

Как измерить ёмкость и индуктивность с помощью генератора и осциллографа + online-калькулятор

Для многих любителей электроники актуальной является задача измерения емкостей конденсаторов и индуктивностей дросселей, поскольку, в отличие от резисторов, эти компоненты нередко бывают не промаркированы (особенно SMD). Между тем, имея генератор синусоидальных колебаний и осциллограф (приборы, которые должны быть в любой радиолюбительской лаборатории), эта задача довольно просто решается. Всё, что для этого нужно — это вспомнить начальный курс электротехники.

Думаю, что многие уже догадались к чему я клоню. Да-да, из последнего уравнения довольно просто вычисляется ёмкость:

C = U_R/U_C * 1/ωR или, с учетом того, что ω= 2πf, получим C = U_R/U_C * 1/2πfR ; (1)

Итак, алгоритм простой: подключаем последовательно с измеряемой ёмкостью резистор, подключаем к этой схеме генератор синусоидальных колебаний и осциллографом измеряем амплитуды напряжений на нашем конденсаторе и резисторе. Изменяя частоту, добиваемся, чтобы амплитуда напряжений на обоих элементах была примерно одинаковой (так измерение получится точнее). Далее, подставляя измеренные значения амплитуд в формулу (1), находим искомую ёмкость конденсатора.

Аналогично можно вывести формулу для подсчета индуктивности:

L = U_L/U_R * R/ω или, с учётом того, что ω= 2πf, получим L = U_L/U_R * R/2πf ; (2)

Таким образом, имея генератор синусоидальных колебаний и осциллограф, с помощью формул (1) и (2) оказывается довольно просто вычислить неизвестную ёмкость или индуктивность (благо резисторы практически всегда имеют маркировку).

Алгоритм действий следующий:

1) Собираем схему из последовательно соединённых резистора известного номинала и исследуемой ёмкости (индуктивности).

2) Подключаем эту схему к генератору синусоидальных колебаний и изменением частоты добиваемся того, чтобы амплитуды напряжений на обоих элементах схемы были примерно одинаковы.

3) По формуле (1) или (2) вычисляем номинал исследуемой ёмкости или индуктивности.

Несмотря на то, что наши элементы не идеальные, есть допуск на номинал резистора и всегда есть некоторые погрешности измерений, результат получается довольно точным (по крайней мере можно без труда идентифицировать ёмкость в стандартном ряду). Пусть у меня при измерении ёмкости получилась величина 1,036 нФ. Очевидно, что на исследуемом конденсаторе должна была быть нанесена маркировка 1 нФ.

Для того, чтобы вам легче было сориентироваться с номиналами резисторов, приведу некоторые примеры:

— для ёмкости 15 пФ в схеме с резистором 200 кОм амплитуды напряжений будут примерно равны на частоте 53 кГц;

— для ёмкости 1 нФ в схеме с резистором 10 кОм амплитуды напряжений будут примерно равны на частоте 15,9 кГц;

— для ёмкости 0,1 мкФ в схеме с резистором 680 Ом амплитуды напряжений будут примерно равны на частоте 2,34 кГц;

— для индуктивности 3 мкГн в схеме с резистором 120 Ом амплитуды напряжений будут примерно равны на частоте 6,3 МГц;

— для индуктивности 100 мкГн в схеме с резистором 120 Ом амплитуды напряжений будут примерно равны на частоте 190 кГц.

Таким образом, диапазон измеряемых емкостей и индуктивностей зависит только от диапазона частот, с которыми могут работать ваши генератор и осциллограф.

На основе этого метода можно изготовить прибор для автоматического измерения емкостей и индуктивностей.

Online-калькулятор для расчёта емкостей и индуктивностей:

(для правильности расчётов используйте в качестве десятичной точки точку, а не запятую)

Источник

Как измерить емкость и индуктивность

Приборы непосредственной оценки и сравнения

Измерение производят балансированием моста в результате попеременной подстройки двух его плеч. Отсчет показаний берется по лимбам рукояток тех плеч, которыми сбалансирован мост.

В качестве примера рассмотрим измерительные мосты, являющиеся основой измерителя индуктивности ЕЗ-3 (рис. 1) и измерителя емкости Е8-3 (рис. 2).

Рис. 1. Схема моста для измерения индуктивности

Рис. 2. Схема моста для измерения емкости с малыми (а) и большими (б) потерями

При балансе моста (рис. 1) индуктивность катушки и ее добротность определяют по формулам Lx = R1R2C2; Qx = wR1C1.

При балансе мостов (рис. 2) измеряемая емкость и сопротивление потерь определяют по формулам

Измерение емкости и индуктивности методом амперметра-вольметра

Для измерения можно воспользоваться схемами рис. 3.

Рисунок 3. Схемы измерения больших (а) и малых (б) сопротивлений переменному току

По показаниям приборов полное сопротивление

из этих выражений можно определить

Когда можно пренебречь активными потерями в конденсаторе или катушке индуктивности, используют схему рис. 4. В этом случае

Рис. 4. Схемы измерения больших (а) и малых (б) сопротивлений методом амперметра — вольтметра

Измерение взаимной индуктивности двух катушек

Измерение взаимной индуктивности двух катушек можно произвести по методу амперметра-вольтметра (рис. 5) и методу последовательно соединенных катушек.

Рис. 5. Измерение взаимной индуктивности по методу амперметра-вольтметра

Значение взаимной индуктивности при измерении по методу амперметра-вольтметра

Измерение индуктивности может быть произведено одним из описанных ранее методов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

• ← на какой частоте излучают холодные межзвездные облака водорода
• на какой частоте искать каналы на приставке →