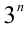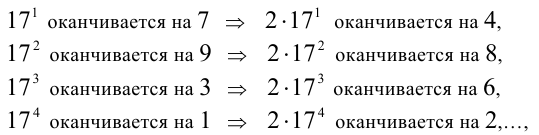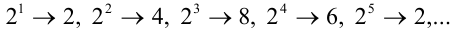на какую цифру оканчивается число 777777
Методическая разработка занятия с одаренными детьми «Степень с натуральным показателем. Сравнение степеней» (6–7-е классы)
Изучение данной темы в младших классах способствует лучшему усвоению тем связанных со степенями в старших классах, формирует познавательный интерес к изучению.
Данная методическая разработка прошла апробацию на занятиях районной очно-заочной математической школы 2006–2009 учебных годах.
Ход занятияЛекционное занятие с учащимися
– Какие из этих действий выполняются всегда? Ответ: сложение, умножение.
– А какие не выполняются? Ответ: не всегда: 15–20, 15:8.
1. Сегодня мы рассмотрим ряд задач на сравнение степеней с натуральными показателями.
Задача 1
Задача 2
Задача 3
2. Задачи на определение цифры, на которую оканчивается число.
Натуральные числа обладают следующим свойством: при умножении ряда чисел, оканчивающихся единицей или “5”, получается число, оканчивающиеся той же цифрой. Например:
581 28911 =581 581…581 = ………..1.
28911 раз
Всякая степень числа оканчивающаяся на “5”, тоже оканчивается на “5”.
Если число оканчивается “6”, то всякая степень числа оканчивается “6”.
Если число оканчивается 76, то любая его степень оканчивается “76”.
Если число оканчивается 25, то любая его степень оканчивается “25”.
Рассмотрим задачи такого типа.
Задача 1
Задача 2
Задачи на делимость
Задача 1
Первое слагаемое делится на 3, второе нет, значит, сумма не делится на 3.
Задача 2
Доказать, что разность 999993 1999 – 777777 1997 кратна 5.
3. Разность данных чисел оканчивается на 0 (7–7=0), 0:5, следовательно разность кратна “5”.
Задачи для индивидуального решения
Задача 1
Задача 2
Задача 3
Задача 4
Задачи для заочной работы
Задача 1
Задача 2
Задача 3
Задача 4
Что больше 
или 
Текстовый документ по теме «Степень числа»
Ищем педагогов в команду «Инфоурок»
Один раз мне на олимпиаде по математике попался вопрос:
„Какой цифрой оканчивается значение выражения 2 в 2013 степени?“
Определение степени я уже знала. Со свойствами степени я была знакома. Но ответить на данный вопрос не смогла. И я поставила перед собой цель:
узнать, какой цифрой оканчивается значение выражения чисел в разных степенях.
выяснить, какой цифрой оканчивается значения выражения от 2 до 10 в степени 2015;
заметить закономерность появления цифр на конце степени числа;
Оказывается, это очень просто узнать…
Если возводить в степень цифру 2,можно кое-что заметить:
2 в первой степени- 2
2 во второй степени- 4
2 в трет ь ей степени- 8
2 в четвёртой степени- 1 6
2 в пятой степени- 3 2
2 в шестой степени- 6 4
2 в седьмой степени- 12 8
2 в восьмой степени- 25 6
2 в девятой степени- 51 2
2 в десятой степени- 102 4
Из наблюдений можно составить таблицу:
Какой же цифрой оканчивается значение выражения 2 в 2013 степени?
Для этого нужно разделить 2013 на 4 с остатком.
После деления в столбик,2013/4=503(ост.1)
Остаток от деления на 4 показателя, будет 1.
Смотрим на таблицу.
И так получаем, что 2 в 2013 степени будет оканчиваться цифрой 2.
Узнаем, какой же цифрой оканчивается значение выражения 2 в 2015 степени.
Делим 2015 на 4.
Из таблицы получаем, что значение выражения 2 в 2015 степени будет оканчиваться цифрой 8.
Итак, будем возводить в степень цифру 3:
3 в первой степени-
3 во второй степени- 9
3 в третей степени-2 7
3 в четвёртой степени-8 1
3 в пятой степени- 24 3
3 в шестой степени-72 9
3 в седьмой степени-218 7
3 в восьмой степени-656 1
3 в девятой степени-1968 3
3 в десятой степени-5404 9
Решим точно так же. 2015 делим на 4 с остатком
Остаток 3. Смотрим в таблицу.
И так получаем, что 3 в 2015 степени, будет оканчиваться цифрой 7.
Рассмотрим ещё и 4 в степени от 1до 10. Имеем:
4 в первой степени: 4
4 во второй степени: 16
4 в третей степени: 64
4 в четвертой степени: 256
4 в пятой степени: 1024
4 в шестой степени: 4096
4 в седьмой степени: 16384
4 в восьмой степени: 65636
4 в девятой степени: 262144
4 в десятой степени: 10485
Если цифру 4 возводить в степень, число будет оканчиваться только на: 4, 6.
„Какой цифрой оканчивается значение выражения 4 в 2015 степени?“
Делим 2015 уже на 2. 2015/2 = 1007 (ост: 1)
Значение выражения 4 в 2015 степени будет оканчиваться цифрой 6
Степень числа 5,6, 10.
5 во второй степени: 25
5 в третьей степени: 125
5 в четвёртой степени: 625
5 в пятой степени: 3125
5 в шестой степени: 15625
5 в седьмой степени: 78125
5 в восьмой степени: 390625
5 в девятой степени: 1953125
5 в десятой степени: 9765625
Если цифру 5 возводить в степень, число будет оканчиваться только на: 5
В какую бы мы степень не возводили цифру 5. Число всё равно будет оканчиваться на 5.
Так же число 6.
В какую бы степень не возводили 6, значение выражения будет оканчиваться на 6.
Ещё число 10, тоже имеет одну цифру на конце.
Продолжим возводить в степень число7.
7 в первой степени: 7
7 во второй степени: 49
7 в третьей степени: 343
7 в четвёртой степени: 2401
7 в пятой степени: 16807
7 в шестой степени: 117649
7 в седьмой степени: 823543
7 в восьмой степени: 5764801
7 в девятой степени: 40353607
7 в десятой степени: 282475249
„Какой цифрой оканчивается значение выражения 7 в 2015 степени?“
Делим 2015 на 4.
2015/4 = 503 (ост: 3). А остатки от деления только 1и 3. Что делать?
Значение выражения 7 в 2015 степени оканчивается той же цифрой, что и 7 в третьей степени, то есть цифрой 3
Возводим в степень число 8.
8 в первой степени: 8
8 во второй степени: 64
8 в третьей степени: 512
8 в четвёртой степени: 4096
8 в пятой степени: 32768
8 в шестой степени: 262144
8 в седьмой степени: 2097152
8 в восьмой степени: 16777216
8 в девятой степени: 134217728
8 в десятой степени: 1073741824
На конце выражения степени числа8 стоят цифры- 8, 4,2,6 –всего 4 цифры.
а 4т+п имеет последней ту же цифру, что число 8 п
Какой цифрой оканчивается значение выражения 8 в 2015 степени?“
9 в первой степени: 9
9 во второй степени: 81
9 в третьей степени: 729
9 в четвёртой степени: 6561
9 в пятой степени: 59049
9 в шестой степени: 531441
9 в седьмой степени: 4782969
9 в восьмой степени: 43046721
9 в девятой степени:4782969
9 в десятой степени: 43046721
Окончание степени числа 9 только 2 числа: 9 и 1
Выражение 9 в 2015 степени оканчивается цифрой 9, так как: 2015 показатель степени нечетный.
Примеры задач.
Примеры задач взяты из интернета « Методическая разработка занятия с одаренными детьми «Степень с натуральным показателем. Сравнение степеней», составленной учителями:
если число оканчивается на 8, то его степени оканчиваются на 8,4,2,6. Повторение через 4.
оканчивается на “5” (1+4=5).
Ответ. Данное выражение оканчивается на “5”
Доказать, что разность 999993 1999 – 777777 1997 кратна 5.
Если число оканчивается на 7, то степень числа оканчивается на 7,9,3,1. повторение через 4.
Разность данных чисел оканчивается на 0 (7–7=0), 0:5, следовательно, разность кратна “5”.
Ответ. Разность кратна 5.
Если степень четная, то число оканчивается на 1, если степень нечетная, то на 9.
99 9 оканчивается на 9, т.к. 9 – нечетное число
число 99 9 – нечетное, т.к. оканчивается на 9.
((999 99 ) 9 оканчивается на 9, т.е. оно нечётное.
((999 999 ) 99 ) 9 оканчивается на 9, т.к. степень нечетная.
Наша сумма оканчивается на 5 (6+7+2=15).
Ответ. Сумма оканчивается на 5, кратна 5.
Ответ. Число оканчивается на 7.
Вывод: Я заметила закономерность появления цифр на конце степени числа. Узнала, какой цифрой оканчивается значение выражения чисел от 2 до 10 в степени 2015
Полученные знания можно применять: в математике, в логических задачах, на олимпиадах.
Литература.
« Методическая разработка занятия с одаренными детьми «Степень с натуральным показателем. Сравнение степеней», составленная учителями:
Информация о числах
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.
Сейчас изучают числа:
Число 777777
Семьсот семьдесят семь тысяч семьсот семьдесят семь
RGB(11, 222, 49) или #0BDE31
(возможное основание)
семья, любовь, доброта, забота, переживания, обида, гармония, равновесие, баланс
Описание числа 777777
Положительное нечетное число 777777 – составное. Сумма цифр: 42. Произведение цифр: 117649. 48 — количество делителей. 1455552 — сумма делителей числа. 777777 и 0.0000012857155714298572 — это обратные числа.
Данное число представляется произведением простых чисел: 3 * 7 * 7 * 11 * 13 * 37.
Косинус: 0.9426, синус: 0.3338, тангенс: 0.3542. Натуральный логарифм числа равен 13.5642. Десятичный логарифм числа: 5.8909. Если из числа извлечь квадратный корень, получится 881.9167, а если кубический — 91.9641
На какую цифру оканчивается число 777777
Задача 15:
Найдите остатки от деления
а) 1989 1990 1991 + 1992³ на 7;
Решение:
Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.
Задача 16:
Докажите, что n³ + 2n делится на 3 для любого натурального n.
Решение:
Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.
Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.
Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.
Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.
Задача 17:
Докажите, что n 5 + 4n делится на 5 при любом натуральном n.
Решение:
Указание: Переберите остатки от деления на 5.
Задача 18:
Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 3.
Задача 19:
Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 9.
Задача 20:
Докажите, что n³ – n делится на 24 при любом нечетном n.
Решение:
Указание: Докажите, что указанное число делится и на 3, и на 8.
Задача 21:
а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.
б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.
Решение:
Указание: Докажите, что указанные числа делятся и на 3 и на 8.
Задача 22:
Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.
Решение:
Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.
Задача 23:
a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.
Решение:
Проверьте, что и a и b делятся и на 3 и на 7.
Задача 24:
a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.
Решение:
Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.
Задача 25:
Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.
Решение:
Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.
Задача 26:
Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.
Решение:
Выясните возможные остатки квадратов при делении на 8.
Задача 27:
Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.
Решение:
Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.
Задача 28:
Решение:
Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 9 = 81), а за 1 – 9 (1 9 = 9).
Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.
Задача 29:
Решение:
Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.
Задача 30:
Решение:
Задача 31:
Найдите остаток от деления 2¹ºº на 3.
Решение:
Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».
Задача 32:
Найдите остаток от деления 3 1989 на 7.
Решение:
Задача 33:
Докажите, что 2222 5555 + 5555²²²² делится на 7.
Решение:
Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.
Задача 34:
Найдите последнюю цифру числа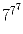 
.
Задача 35:
а) p, p + 10, p + 14 – простые числа. Найдите p.
б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.
Решение:
Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.
Задача 36:
p и 8p² + 1 – простые числа. Найдите p.
Решение:
Задача 37:
p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.
Решение:
Задача 38:
Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.
Решение:
Рассмотрите остатки по модулю 3.
Задача 39:
а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?
б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 40:
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 41:
p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.
Ответ: p = 5. Рассмотрите остатки при делении на 5.
Задача 42:
Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.
Решение:
Это число дает остаток 7 от деления на 9.
Задача 43:
Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.
Решение:
Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.
Задача 44:
Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.
Решение:
Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.
Задача 45:
x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.
Решение:
Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.
Метод анализа последней цифры числа
Метод анализа последней цифры числа
В ряде случаев удобным оказывается так называемый метод анализа последней (последних) цифры числа.
Пример №30.
Доказать, что число 19981999200020012002 не является квадратом целого числа.
Доказательство. Натуральное число п может оканчиваться на любую из десяти цифр: 0, 1,2, 3, 4, 5, 6, 7, 8, 9. Выясним, на какую цифру при этом может оканчиваться квадрат этого числа:
Среди цифр, на которые оканчивается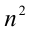 
, отсутствует цифра «2». Поэтому данное число не может являться квадратом целого числа.
Пример №31.
Доказать, что ни при каком натуральном п число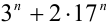 
не является квадратом натурального числа.
Решение:
Выясним, на какую цифру может оканчиваться число 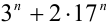. Сделаем это последовательно. Сначала оценим последнюю цифру числа 
далее эта последовательность последних цифр 3,9,7,1,3,9,7,1,… циклически повторяется. Оценим теперь последние цифры чисел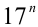 
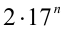
и 
:
далее последовательность последних цифр 4,8,6,2,… также циклически повторяется. Суммируя, получаем,что
и далее эта последовательность последних цифр выражения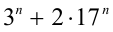 
опять-таки циклически (с периодом 4) повторяется.
Таким образом, методом анализа последней цифры удалось установить, что при любых натуральных п число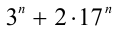 
может оканчиваться только на цифры 3 или 7. Но квадрат никакого натурального числа этими цифрами не оканчивается (квадрат натурального числа может оканчиваться только на одну из цифр 0, 1,4, 5, 6, 9), что и доказывает утверждение.
Пример №32.
Найти последнюю цифру числа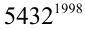 
.
Решение:
Решим сначала более простую задачу, а именно найдём последнюю цифру числа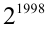 
. Выясним, на какие цифры может оканчиваться натуральная степень числа 2:
Очевидно, что при дальнейшем увеличении показателя степени последовательность последних цифр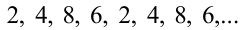 
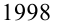
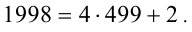
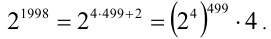
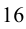
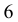
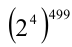
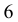
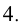
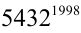
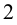
будет циклически повторяться. Представим число 
в виде: 
Имеем: 
Заметим, что число 
в скобках оканчивается цифрой 
, и поэтому любая его натуральная степень также будет оканчиваться этой цифрой. Итак, число 
оканчивается цифрой , и это число умножается на четыре. Поэтому последней цифрой их произведения будет 
Если теперь повторить проведенные рассуждения для числа 
, то окажется (сделайте это самостоятельно), что добавление одной или нескольких цифр перед 
не оказывает влияния на полученный результат.
Ответ: число оканчивается цифрой
Пример №33.
Существует ли такое натуральное число n ,что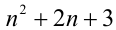 
делится нацело на 2005?
Решение:
Последней цифрой у натурального числа n может быть любая из цифр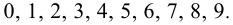 
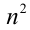
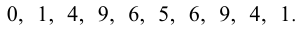
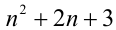
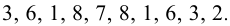
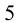
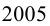
Последней цифрой у числа 
может быть соответственно 
Тогда последняя цифра у числа , как несложно посчитать, может соответственно принимать значения 
Но тогда это число не делится даже на 
, а значит, не может делиться и на 
.
Существуют задачи, решение которых опирается на знание определений и свойств специфических групп целых чисел или же на определённые понятия. К таким задачам можно отнести задачи на простые числа, а также на НОК и НОД. Для их решения разработаны, в том числе, специальные приёмы, учитывающие их специфику. Рассмотрим примеры задач этого типа.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
- на какую цифру оканчивается число 222222
- на какую цифру ставить морозильную камеру в холодильнике атлант