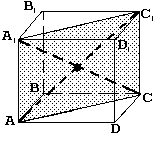
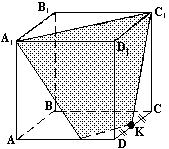
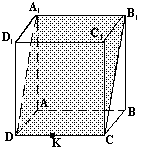
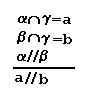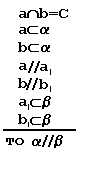На рисунке изображен куб докажите что прямые аа1 и в1с1
На рисунке изображен куб докажите что прямые аа1 и в1с1
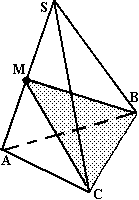
Постройте сечение куба, проходящее через точки M, N и P. Определите вид треугольника, являющегося сечением.
Точки M и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, тогда соединяем M и N сплошной линией. Аналогично строим прямую NP. Точки P и M лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок PM. Он невидимый, тогда соединяем P и N штрихом. Треугольник MNP — искомое сечение.
Так как это куб, то треугольник, являющийся сечением — равносторонний.
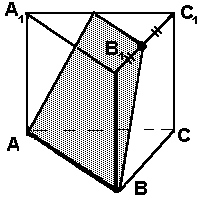
Постройте сечение куба, проходящее через точки M, N и P. Определите вид треугольника, являющегося сечением.
Аналоги к заданию № 1812: 1813 Все
Постройте сечение куба, проходящее через точки M, N и P. Определите вид треугольника, являющегося сечением.
Точки M и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он невидимый, тогда соединяем M и N штрихом. Аналогично строим прямую MP. Точки P и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок PN. Он видимый, тогда соединяем P и N сплошной линией. Треугольник MNP — искомое сечение.
Так как это куб, то треугольник, являющийся сечением — равнобедренный остроугольный.
На рисунке изображен куб докажите что прямые аа1 и в1с1
Особенность человеческого мышления такова, что даже простейшее восприятие и запоминание требуют неоднократного обращения к материалу. Начальные темы стереометрии изучаются длительное время,поэтому процесс забывания неизбежен. Следовательно, программой необходимо предусмотреть уроки тематического повторения, работающие на перспективу применения этих знаний в новой ситуации.
Каковы бы ни были формы урока все они направлены на достижение следующих целей:
Цели уроков методической разработки.
1.Дидактические.
а) Наилучший способ обучения учащихся, дающий им сознательные и прочные знания и обеспечивачший одновременное их умственное развитие заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теоретические практические задачи,решение которые дает им новые знания.
б) Обучение на немногочисленных, но хорошо подобранных задачах решаемых школьниками в основном самостоятельно, способствует вовлечению их в творческую исследовательскую работу, последовательно проводя через этапы научного поиска.
в) С помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями.
г) Усвоение материала курса через последовательное решение учебных задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой активности учащихся.
2. Общекультурные и научные (геометрические).
К ним относится развитие вербально-логического, наглядно-действенного (практического) наглядно-образного, пространственного, визуального и др. типов мышления,развитие свойств интелекта:
а) геометрическая интуиция на образы, свойства, методы построения.
б) пространственное мышление (одно-, двух-, трех мерное евклидовое пространство), пространственные абстракции, их общность, анализ и синтез геометрических образов, пространственное воображение.
в) логическое мышление (владение правилами логического вывода и построения, владение разными методами геометрии)
г) способность к конструктивно-геометрической деятельности.
д) владение символическим языком геометрии.
3. Воспитательные.
Аккуратность, коллективизм, ответственность за себя и товарищей, дружбу, любовь к предмету и др.
4. Прикладные.
Умение анализировать задачу, работать с учебником, применять свои знания в новой ситуации.
ТЕМЫ выступлений для урока
1. Аксиомы стереометрии (таблицы остаются учащимся для работы).
А 1. Через любые две точки пространства проходит единственная прямая.
А 2. Через любые три точки пространства, не лежащие на одной прямой, проходит единственная плоскость.
А 3. Если две плоскости имеют общую точку, то они пересекаются по прямой.
В ходе беседы выделяются существенные моменты теории:
а) разъяснить содержание аксиом и иллюстрировать на модели;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
г) запись содержания с помощью символов.
| Чертеж. | Формулировка. | |
|---|---|---|
| Сл.1 |  | Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. |
| Сл.2 |  | Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну. |
| Сл.3. |  | Через две пересекающиеся прямые можно провести плоскость и притом только одну. |
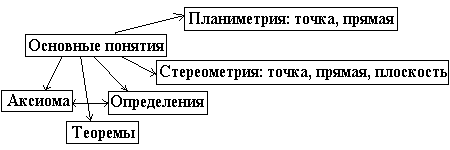
В заключение предлагается схема логического строения геометрии (заготовленная заранее):
3. а) Взаимное расположение в пространстве двух прямых.
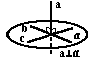
б) Взаимное расположение в пространстве прямой и плоскости.
в) Взаимное расположение в пространстве двух плоскостей.
 |  |  |  | ||
 |  |  |  | ||
 |  |  | |||
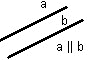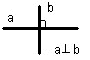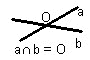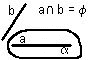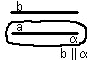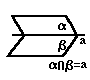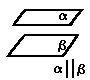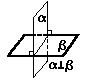г) Свойства, связывающие понятие параллельности двух плоскостей с понятием параллельности двух прямых.
Теорема. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
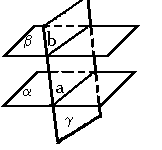
Теорема (признак). Если две пересекающиеся приямые одной плосткости соответственно параллельны двум прямым другой плосткости, то эти плоскости параллельны.
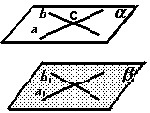
4. Способы задания плоскостей.
| Способы задания плоскостей | Рисунок | |
|---|---|---|
| I. По трем точкам | 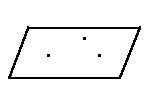 | A2 |
| 2. По прямой и непринадлежащей ей точке. | 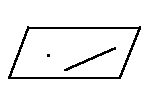 | Cл 2 |
| 3. По двум пересекающимся прямым. | 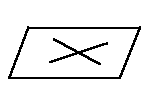 | Cл 3 |
| 4. По двум параллельным прямым. | 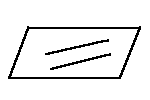 | определение параллельных прямых |
5. Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики:
Примеры и их решение приводят учащиеся (под руководством учителя).
AA1//CC1
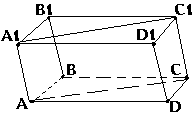
6. Постороение сечений с использованием свойств параллельных плоскостей.
P=16+8
=8(2+)см
P=8+4=4(2+)см
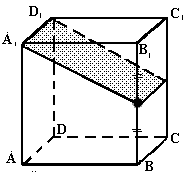
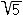
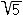
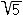
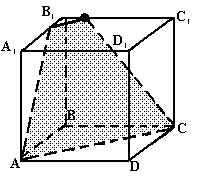
N3. Определите вид сечения (и постройте его) куба АВСДА 1 В 1 С 1 Д 1 плостокстью, проходящей через точку М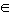 
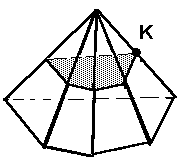
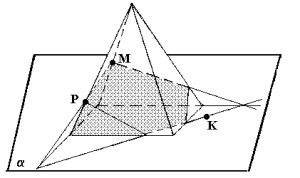
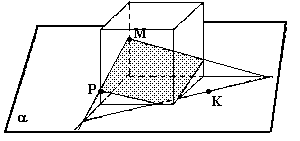
В 1 С 1 и диагональ нижнего основания.
N2. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды.
Урок 2. Лабораторная работа. (1 час).
Проведение лабораторных работ позволяет привлечь внимание учащихся к математике, сформировать интерес к ней. Форма проведения лабораторных работ отвечает индивидуальным особенностям обучения учащихся, способствует активизации их математической деятельности. Лабораторная работа проводится на два варианта (В-I, В-2).
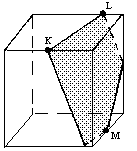
N1. Постройте сечение куба по трем точкам, расположенным так, как
а) показано на рисунке:
| В-1 | В-2 |
|---|---|
 |  |
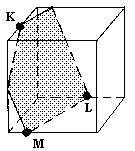б) Постороить сечение параллелепипеда плоскостью, проходящей через точки М, Р, К.
| В-1 | В-2 |
|---|---|
 |  |
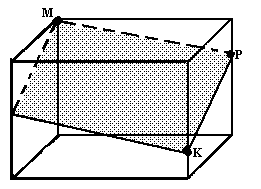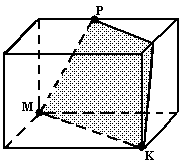N2. (Задача на использование свойств параллельности прямой и плоскости).
a)
 |  |
|---|
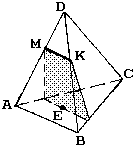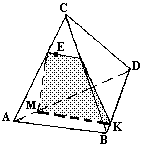б)
 |  |
|---|
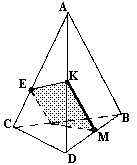N3. (Задача на использование свойств параллельных плоскостей).
N4. Постороить сечение многогранника плоскостью, проходящей через точки
В-1
N5. Творческое задание.
Составить две задачи на построение сечений многогранников с использованием полученных знаний.
Решение задач лабораторной работы должно сопровождаться работой учащихся на моделях, изготовленных из спиц, спичек, пластилина или пенопласта. Учащиеся должны изготовить сечения из картона и использовать его при выполнении чертежа на бумаге. Такой поиск решения (руками) помогает при построении сечения.
На рисунке изображен куб докажите что прямые аа1 и в1с1
Особенность человеческого мышления такова, что даже простейшее восприятие и запоминание требуют неоднократного обращения к материалу. Начальные темы стереометрии изучаются длительное время,поэтому процесс забывания неизбежен. Следовательно, программой необходимо предусмотреть уроки тематического повторения, работающие на перспективу применения этих знаний в новой ситуации.
Каковы бы ни были формы урока все они направлены на достижение следующих целей:
Цели уроков методической разработки.
1.Дидактические.
а) Наилучший способ обучения учащихся, дающий им сознательные и прочные знания и обеспечивачший одновременное их умственное развитие заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теоретические практические задачи,решение которые дает им новые знания.
б) Обучение на немногочисленных, но хорошо подобранных задачах решаемых школьниками в основном самостоятельно, способствует вовлечению их в творческую исследовательскую работу, последовательно проводя через этапы научного поиска.
в) С помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями.
г) Усвоение материала курса через последовательное решение учебных задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой активности учащихся.
2. Общекультурные и научные (геометрические).
К ним относится развитие вербально-логического, наглядно-действенного (практического) наглядно-образного, пространственного, визуального и др. типов мышления,развитие свойств интелекта:
а) геометрическая интуиция на образы, свойства, методы построения.
б) пространственное мышление (одно-, двух-, трех мерное евклидовое пространство), пространственные абстракции, их общность, анализ и синтез геометрических образов, пространственное воображение.
в) логическое мышление (владение правилами логического вывода и построения, владение разными методами геометрии)
г) способность к конструктивно-геометрической деятельности.
д) владение символическим языком геометрии.
3. Воспитательные.
Аккуратность, коллективизм, ответственность за себя и товарищей, дружбу, любовь к предмету и др.
4. Прикладные.
Умение анализировать задачу, работать с учебником, применять свои знания в новой ситуации.
ТЕМЫ выступлений для урока
1. Аксиомы стереометрии (таблицы остаются учащимся для работы).
А 1. Через любые две точки пространства проходит единственная прямая.
А 2. Через любые три точки пространства, не лежащие на одной прямой, проходит единственная плоскость.
А 3. Если две плоскости имеют общую точку, то они пересекаются по прямой.
В ходе беседы выделяются существенные моменты теории:
а) разъяснить содержание аксиом и иллюстрировать на модели;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
г) запись содержания с помощью символов.
| Чертеж. | Формулировка. | |
|---|---|---|
| Сл.1 | | Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. |
| Сл.2 | | Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну. |
| Сл.3. | | Через две пересекающиеся прямые можно провести плоскость и притом только одну. |
В заключение предлагается схема логического строения геометрии (заготовленная заранее):
3. а) Взаимное расположение в пространстве двух прямых.
б) Взаимное расположение в пространстве прямой и плоскости.
в) Взаимное расположение в пространстве двух плоскостей.
| | | | ||
| | | | ||
| | | |||
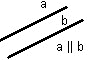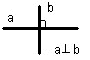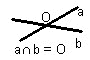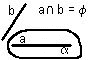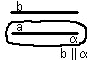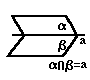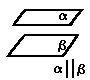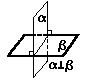г) Свойства, связывающие понятие параллельности двух плоскостей с понятием параллельности двух прямых.
Теорема. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Теорема (признак). Если две пересекающиеся приямые одной плосткости соответственно параллельны двум прямым другой плосткости, то эти плоскости параллельны.
4. Способы задания плоскостей.
| Способы задания плоскостей | Рисунок | |
|---|---|---|
| I. По трем точкам | | A2 |
| 2. По прямой и непринадлежащей ей точке. | | Cл 2 |
| 3. По двум пересекающимся прямым. | | Cл 3 |
| 4. По двум параллельным прямым. | | определение параллельных прямых |
5. Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики:
Примеры и их решение приводят учащиеся (под руководством учителя).
AA1//CC1
6. Постороение сечений с использованием свойств параллельных плоскостей.
P=16+8=8(2+)см
P=8+4=4(2+)см
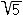
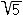
N3. Определите вид сечения (и постройте его) куба АВСДА 1 В 1 С 1 Д 1 плостокстью, проходящей через точку М В 1 С 1 и диагональ нижнего основания.
N2. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды.
Урок 2. Лабораторная работа. (1 час).
Проведение лабораторных работ позволяет привлечь внимание учащихся к математике, сформировать интерес к ней. Форма проведения лабораторных работ отвечает индивидуальным особенностям обучения учащихся, способствует активизации их математической деятельности. Лабораторная работа проводится на два варианта (В-I, В-2).
N1. Постройте сечение куба по трем точкам, расположенным так, как
а) показано на рисунке:
| В-1 | В-2 |
|---|---|
| |
б) Постороить сечение параллелепипеда плоскостью, проходящей через точки М, Р, К.
| В-1 | В-2 |
|---|---|
| |
N2. (Задача на использование свойств параллельности прямой и плоскости).
a)
| |
|---|
б)
| |
|---|
N3. (Задача на использование свойств параллельных плоскостей).
N4. Постороить сечение многогранника плоскостью, проходящей через точки
В-1
N5. Творческое задание.
Составить две задачи на построение сечений многогранников с использованием полученных знаний.
Решение задач лабораторной работы должно сопровождаться работой учащихся на моделях, изготовленных из спиц, спичек, пластилина или пенопласта. Учащиеся должны изготовить сечения из картона и использовать его при выполнении чертежа на бумаге. Такой поиск решения (руками) помогает при построении сечения.