наименьшее двузначное число это какое число
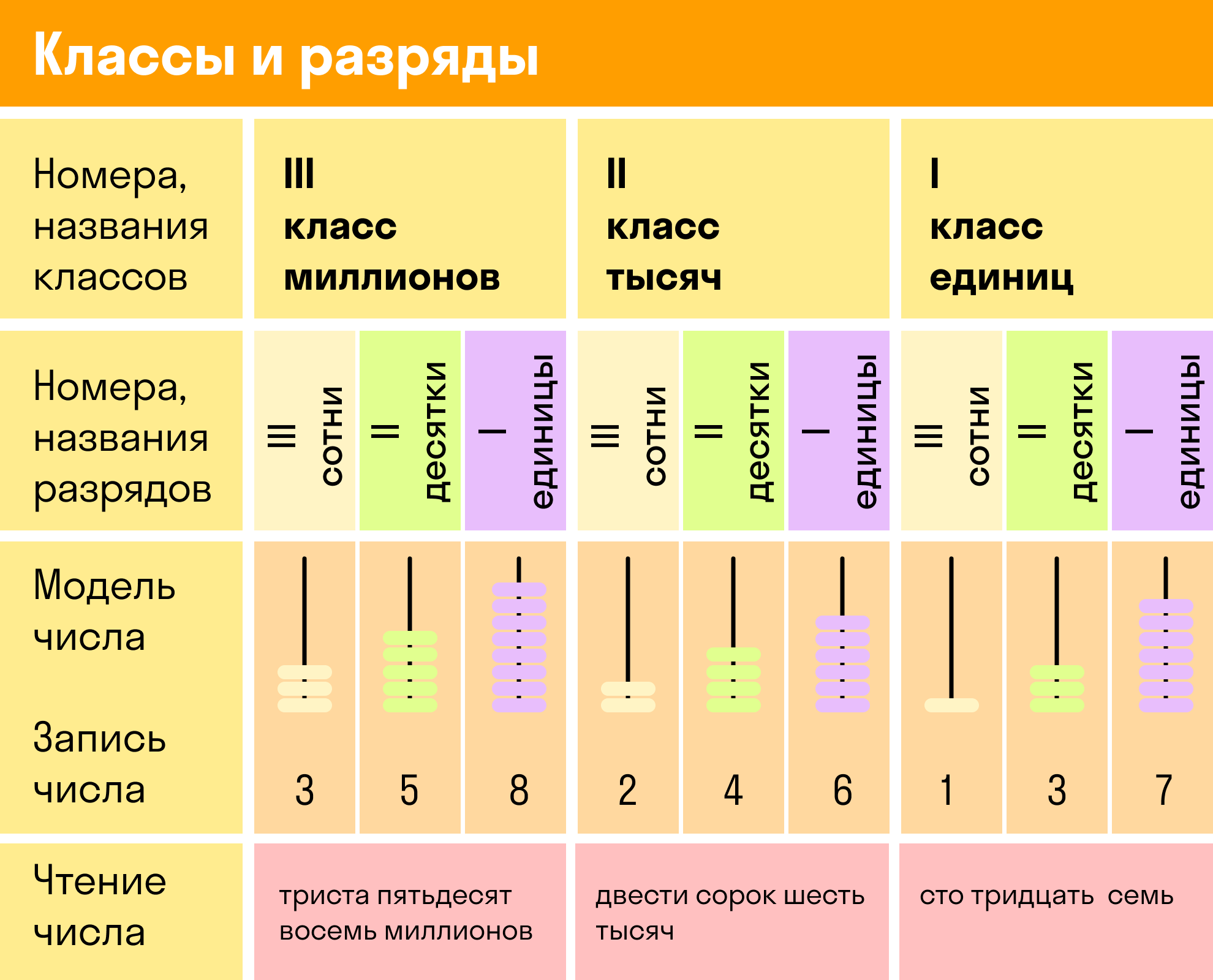
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
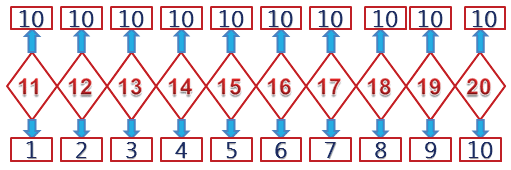
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, …
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы по математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это неправильные примеры натуральных чисел, потому что ноль расположен слева. По правилам так нельзя. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
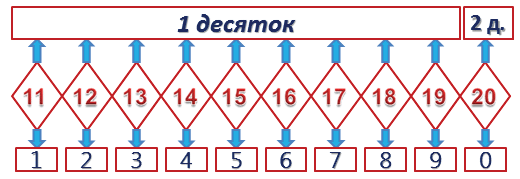
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двухзначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа на него самого | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Числа от 1 до 100. Состав числа. Круглые числа
Числа от 1 до 100
Предыдущее и последующее число
56 , 57
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
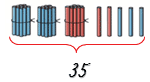
Состав двузначного числа
Всего на рисунке 35 палочкек.
35 = 30 + 5
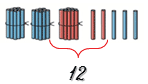
Красных палочек 12.
12 = 10 + 2
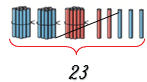
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
Круглые числа
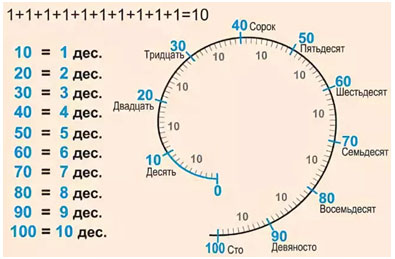
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
10 + 40 = 50
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:
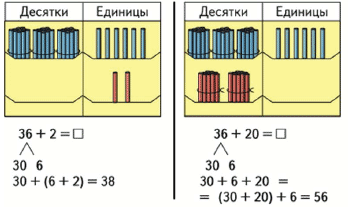
Действия с десятками и единицами
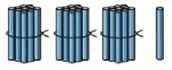
Как решить пример 34 + 25?
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
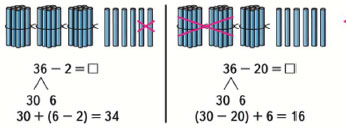
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях:
Наименьшее двузначное число. Счётная единица «десяток». Состав числа 10.
Ищем педагогов в команду «Инфоурок»
Выбранный для просмотра документ Наименьшее двузначное число. Счётная единица десяток. Состав числа 10..docx
План-конспект урока по учебнику
«Математика. 1 класс».
Автор: Н.Б. Истомина
Тема: Наименьшее двузначное число. Счётная единица «десяток». Состав числа 10.
Наименьшее двузначное число. Счётная единица «десяток». Состав числа 10
Рассмотреть все случаи записи наименьшего двузначного числа10 в виде суммы двух слагаемых, используя предметную модель десятка и единицы. Дать установку на запоминание состава числа 10.
Записывать двузначное число по его названию
Записывать двузначное число цифрами, пользуясь его предметной моделью
Использовать предметные модели (десятка и единиц) для обоснования записи и чтения двузначных чисел.
Моделировать состав числа 10, используя предметные, графические, символические модели.
Запись числа 10 цифрами 1 и 0. Модели десятка и единицы.
Окружающий мир, литературное чтение, технология
Учебник Н.Б. Истомина « Математика» 2 часть
Тема: «Наименьшее двузначное число. Счётная единица «десяток». Состав числа 10»
ТСО, таблицы моделей десятка и единиц.
Работа фронтальная, индивидуальная, в парах, в группах.
ТЕХНОЛОГИЯ ПРОБЛЕМНОГО ДИАЛОГА
Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов
I . Мотивация к учебной деятельности
Подготовка учащихся к уроку.
Уточняет тематические рамки.
Проверяет готовность обучающихся к уроку.
— Давайте улыбнемся друг другу. Пусть урок принесет нам всем радость общения.
-Сегодня на уроке, ребята, вас ожидает много интересных заданий, новых открытий, а помощниками вам будут: внимание, находчивость, смекалка.
-В своих тетрадях в «квадратике настроения» выразите символом свое настроение в начале урока. (слайд1)
Дети настраиваются на работу.
Дети с помощью условного знака выражают своё настроение.
личностная мотивация учебной деятельности
Коммуникативные : планирование учебного сотрудничества с учителем и сверстниками.
II . Формулирование темы урока, постановка цели (3-4мин)
Цели:— подведение детей к формулированию темы и постановке задач урока. Составление плана работы
Проводят связь между предметами «Математика» и «Окружающий мир»
Ставят цели, формулируют (уточняют) тему урока
Озвучивает тему и цель урока. Уточняет понимание учащимися поставленных целей урока.
Ребята, скажите какое сегодня число?
Продолжите число 9- это…
– В воздухе кружатся легкие снежинки.
Мы снежинки, мы пушинки,
Покружиться мы не прочь.
Мы снежинки – балеринки,
Мы танцуем день и ночь.
Мы деревья побелили –
Крыши пухом замели.
Землю бархатом укрыли,
И от стужи сберегли.
Посчитайте снежинки и запишите каждое число, которое вы называете.
Сравните свою запись с записью на слайде. (2)
Скажите ребята, есть ли среди вас, те у которых запись аналогична?
А кто испытывал трудности? В какой момент вы испытывали трудность?
Догадались, с каким числом мы будем сегодня работать? Назовите тему. (Уточняет тему урока) «Число 10 – самое маленькое двузначное число. Счётная единица «десяток». Состав числа 10». Именно так звучит тема нашего урока. (слайд3)
Проанализируйте трудности выполнения задания.
Цель: Знакомство с числом 10.
Предположите способ решения выполнения этой проблемы.
Число 9 – однозначное число, самое большое однозначное число. Соседи …
Февраль последний месяц зимы.
(дети называют изменения природы, отмеченные во время прогулки)
Сравнивают свой результат, производят оценку своей работы.
Определяют тему урока. Число 10.
Озвучивают трудность при записи числа 10.
1. Научиться читать и записывать число 10.
Познавательные: самостоятельное выделение-формулирование познавательной цели, формулирование проблемы.
планирование учебного сотрудничества с учителем и сверстниками
III . Изучение нового
Побуждающий от проблемной ситуации диалог, Побуждающий к выдвижению и проверке гипотез диалог
Составляют план достижения цели и определяют средства
Проводят коллективное исследование
Применяют новый способ. Отработка операций, в которых допущены ошибки.
Осуществляют взаимный контроль и оказывают в сотрудничестве необходимую взаимопомощь (работают в парах
Выполняют работу, анализируют, контролируют и оценивают результат
Проводит параллель с ранее изученным материалом.
Подводит обучающихся к выводу о правилах записи числа 10.
Создает эмоциональный настрой на работу
Организует учебное исследование для выделения понятия.
в обсуждение проблемных вопросов
Предположите, для чего мы будем изучать это число?
Определите следующую задачу.
Изадача, каждого урока.
Назовите последнее число записанное вами.
Проанализируйте запись числа 10 с записью всех предыдущих чисел ряда. Своими наблюдениями поделитесь в паре. А теперь откройте учебники на странице 37 и сравните свой вывод с
записью на голубой плашке в учебнике. У какой пары совпали наблюдения?
А теперь посмотрите, как правильно записывается это число. Слайд №4.
Запишите число 10 по образцу в тетрадях. Но прежде, напомните тихонько правила работы в тетрадях друг другу.
Какую задачу урока мы решали? (слайд5) Какие действия мы для этого выполнили?
Что нужно помнить, чтобы записать число 10 в тетради?
Оцените работу друг друга. По каким критериям мы будем оценивать работу?
Послушайте стихотворение, посвящённое этому числу в исполнении Стёпы.
Для упражнения в чтении этого числа предлагаю поработать в научной лаборатории. Проведите исследовательскую работу над числом 10.(карточки)
Поработайте в группах и сделайте вывод.
1.Число 10 следует за числом ____.
2.Число 10 ___________ всех чисел, которые стоят справа от него в натуральном ряду чисел.
3.Число 10 стоит перед числом ___.
4.Число 10 находится между числами ___ и ____.
5.Число 10 больше числа 9 на ___.
6.Для записи числа 10 понадобится ___ цифры.
7. Значит число 10_________.
(Обобщение – слайд 7)
Выберите из поставленных нами следующий пункт задачи урока. (Слайд 8)
Выберите способ решения этой проблемы.
Игра «Кто быстрее?» (по рядам)
№ 82 стр.37 (на слайдах 9,10).
Проверьте и оцените работу по алгоритму. (Слайд 11)
Проанализируйте, по какому признаку можно разложить квадраты на две группы. Выполните задание в парах на стр. 38 № 83
Проверка, какие равенства можно составить по признакам, на которые вы разложили фигуры?
— Для использования счёта.
2.Постараться запомнить состав числа 10.
3. Работать над развитием речи.
Сравнивают, делятся в паре своими наблюдениями, читают вывод в учебнике.
Записывают в тетрадях по образцу.
Учились писать число 10. Для этого мы наблюдали, как записывается это число.
Аккуратность, правильная запись числа.
Обмениваются тетрадями в парах, оценивают знаком.
Цифра вроде буквы О –
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева рядом с ним единицу примостим
Он побольше станет весить
Потому что это – десять.
Работают в группах, делают вывод.
Каждая группа отвечает на 1 вопрос.
Число 10 самое маленькое двузначное число. Для записи используются цифры 1 и 0.
Выбирают и называют.
Записывают самостоятельно, проверяют. Оценивают свою работу.
Оцените работу пары. По какому признаку мы оценим работу пары? (как договаривались работать).
Коммуникативные: инициативное сотрудничество в поиске и выборе информации.
— составление плана и последовательности действий
Исследуют условия учебной задачи, обсуждают предметные способы решения
IV . Закрепление нового (15 мин)
Цель:— освоение способа действия с полученными знаниями в практической деятельности
Решают типовые задания с проговариванием алгоритма вслух
Устанавливает осознанность восприятия, первичное обобщение, побуждает к высказыванию своего мнения.
Обеспечивает положительную реакцию детей на творчество одноклассников.
Акцентирует внимание на конечных результатах учебной деятельности обучающихся на уроке
Игра «Кто внимательный».
Коллективная работа составление и запись с использованием доски левого столбика картинок. Равенства, составленные по правому столбику картинок, запишите самостоятельно.
Что объединяет все записанные равенства?
Используя равенства, в парах расскажите друг другу.
Какую проблему мы сейчас выполняли? Что мы для этого делали?
Чья работа вам понравилась? Почему?
Вспомните правила безопасности при работе с ножницами.
Выполните работу в группах №85. Используйте памятку (слайд 12)
Какое открытие вы сделали, выполняя это задание?
Составляют и записывают равенства. Первые три с объяснением далее самостоятельно. Один обучающийся на обратной стороне доски.
Оценивают работу товарища.
Выполняют № 85, работая в группе.
Озвучивают свой результат.
Познавательные: умение структурировать знания, выбор наиболее эффективных способов решения задания, умение осознанно и произвольно строить высказывания.
Коммуникативные : управление поведением партнера, контроль, коррекция, оценка действий партнера.
Регулятивные : Контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
Регулятивная Осуществляют пошаговый контроль по результату
V . Контролирующее задание (12 мин)
-осознание каждым обучающимся степени овладения полученных знаний
Осуществляют: самооценку; самопроверку; взаимопроверку; предварительную оценку.
Контролирует выполнение работы.
Организует: взаимопроверку; коллективную проверку; проверку выполнения упражнения; беседу по уточнению и конкретизации первичных знаний; оценочные высказывания обучающихся; обсуждение способов решения; поисковую работу обучающихся (постановка цели и план действий); самостоятельную работу с учебником; беседу, связывая результаты урока с его целями.
Запишите равенство, которое соответствует рисунку
Оцени свою работу (обу-ся, работающему на доске. По какому правилу ты оценил свою работу так?)
Для чего мы выполняли это задание?
Прочитайте вывод в рамочке на стр. 39 и постарайтесь его запомнить. Расскажите состав числа друг другу.
Докажите, что мы справились с этой проблемой.
Выделите из всего сказанного вами в течение урока, ту часть, которую можно отнести к третьей проблеме.
Повторяют состав числа 10.
Оцените работу друг друга. По правилу. (используют таблицу оценки результатов)
Закрепляли состав числа 10.
Дети по очереди называют состав числа 10.
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения, внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта; выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
Личностные: личностное, профессиональное, жизненное самоопределение и построение жизненных планов во временной перспективе.
VII . Рефлексия учебной деятельности на уроке (3 мин)
Цели:— соотнесение поставленных задач с достигнутым результатом, фиксация нового знания, постановка дальнейших целей
. Формулируют конечный результат своей работы на уроке.
Называют основные позиции нового материала и как они их усвоили (что получилось, что не получилось и почему)
Отмечает степень вовлеченности учащихся
в работу на уроке.
Какое число мы сегодня исследовали?
Какие открытия мы сделали в ходе исследования?
«Знаете ли вы?» (слайд 13)
Десятком можно назвать 10 любых предметов.
Например, отгадайте загадку.
А ещё что можно считать десятками? (слайд 14)
А какие ещё двузначные числа вы можете назвать? А где в жизни мы встречаемся с двузначными числами?
Количество, каких предметов в классе можно обозначить двузначным числом? А можете ли вы записать числом количество парт в нашем классе? А хотите научиться? Поверите ли вы мне, что уже завтра мы сможем справиться с этой проблемой? Эту загадку нам поможет решить следующий урок.
В своих тетрадях в «квадратике настроения» выразите символом свое настроение в конце урока.
Делятся открытием, используя алгоритм
Отгадывают загадку, называют предметы, которые считают десятками, отвечают на вопросы учителя.
(№ страницы, квартиры, дома, возраст человека)
(парты, стулья, количество обучающихся, тетрадей, учебников)
Рисуют свое настроение в конце урока.
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли.
Познавательные : рефлексия способов и условий действия, их контроль и оценка; критичность
Личностные : установление учащимся значения результатов своей деятельности для удовлетворения своих потребностей, мотивов, жизненных интересов.
Выбранный для просмотра документ Наименьшее двузначное число.pptx
Описание презентации по отдельным слайдам:
1 2 3 4 5 6 7 8 9 10
Тема: Задачи: «Число 10 – самое маленькое двузначное число. Счётная единица «десяток». Состав числа 10». 1. Научиться читать и записывать число 10. 2.Постараться запомнить состав числа 10. 3. Работать над развитием речи. Цель: знакомство с числом 10.
Задачи: 1. Научиться читать и записывать число 10.
1. Число 10 самое маленькое двузначное число. 2. Для записи используются цифры 1 и 0.
Задачи урока: Научиться читать и записывать число 10. Постараться запомнить состав числа 10. Работать над развитием речи.
4+6=10 3+7=10 5+5=10 6+4=10 7+3=10 10-5=5 10-4=6 10-3=7 10-6=4 10-7=3 Проверьте
Прочитайте задание. Распределите задания между собой. Сравните с образцом в учебнике. Прочитайте вывод в учебнике. Озвучьте свой вывод.
Знаете ли вы? Есть у нас работники, Во всём помочь охотники. Целый десяток Верных ребяток.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДВ-280885
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Приамурье начнут пускать на занятия только привитых студентов
Время чтения: 0 минут
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
Российские педагоги чаще всего жалуются на излишнюю отчетность и низкую зарплату
Время чтения: 2 минуты
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
В Москве разработают дизайн-код для школ и детсадов
Время чтения: 1 минута
Минобрнауки утвердило перечень вступительных экзаменов в вузы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.