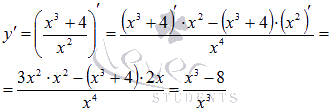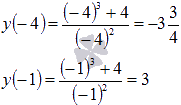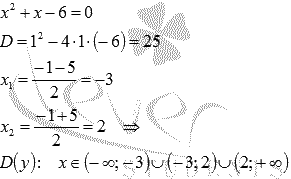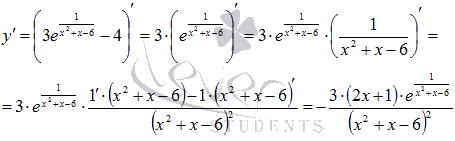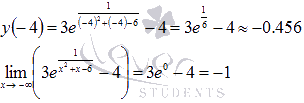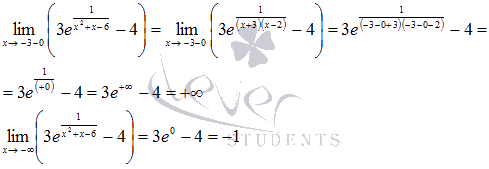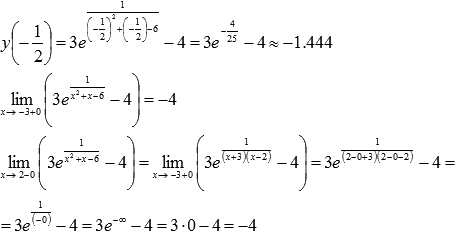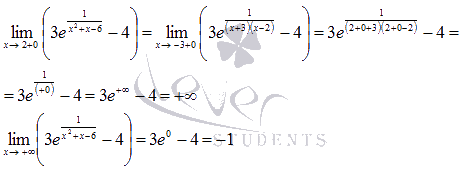Наименьшее значение чему равно
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Основные определения
Начнем, как всегда, с формулировки основных определений.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
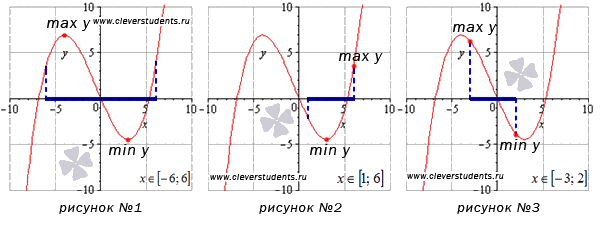
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
Наибольшее и наименьшее значение функции на открытом интервале
Наибольшее и наименьшее значение функции на бесконечности
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Решение:
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
Следовательно, производные функции существуют на всей области ее определения.
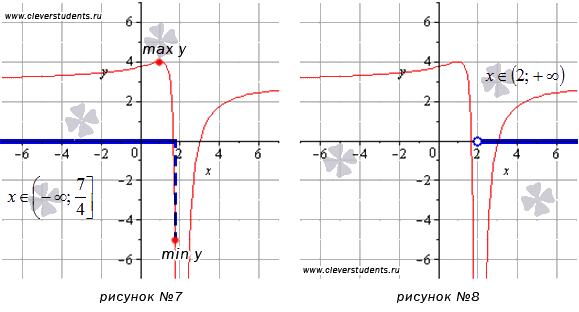
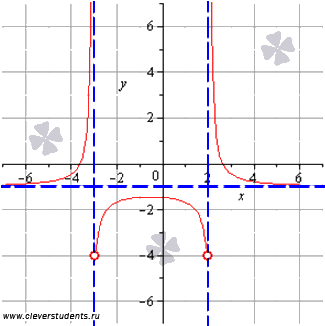
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Наибольшее и наименьшее значение функции.
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Навигация по странице.
Кратко остановимся на основных определениях.
Наибольшим значением функции y=f(x) на промежутке X называют такое значение 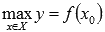
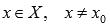
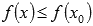
Наименьшим значением функции y=f(x) на промежутке X называют такое значение 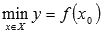
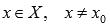
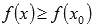
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе 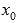
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
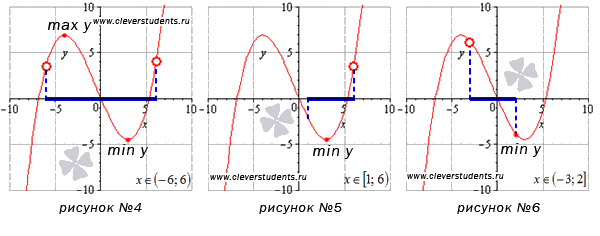
На интервале [1;6) наименьшее значение функции достигается в стационарной точке, а про наибольшее значение мы ничего сказать не можем. Если бы точка x=6 была частью интервала, тогда при этом значении функция принимала бы наибольшее значение. Этот пример изображен на рисунке №5.
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть 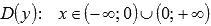
Находим производную функции по правилу дифференцирования дроби:
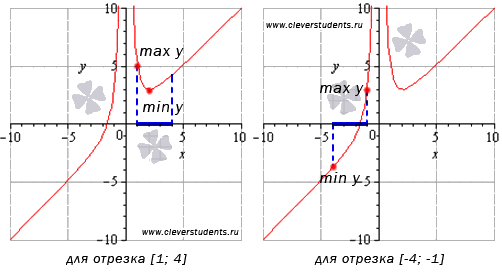
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):
Следовательно, 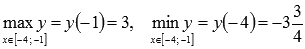
Прежде чем ознакомиться с алгоритмом нахождения наибольшего и наименьшего значения функции на открытом или бесконечном интервале рекомендуем повторить определения одностороннего предела и предела на бесконечности, а также способы нахождения пределов.
Проверяем, является ли интервал X подмножеством области определения функции.
Находим все точки, в которых не существует первая производная и которые содержатся в интервале X (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
Если стационарных точек нет или ни одна из них не попадает в интервал, то переходим к следующему пункту.
Вычисляем значения функции в стационарных точках и точках, в которых не существует первая производная функции (если такие точки есть).
Делаем выводы, отталкиваясь от полученных значений функции и пределов. Здесь может быть масса вариантов. К примеру, если односторонний предел равен минус бесконечности (плюс бесконечности), то о наименьшем (наибольшем) значении функции ничего сказать нельзя для данного интервала. Ниже разобраны несколько типичных примеров. Надеемся подробные описания их решения помогут Вам усвоить тему. Рекомендуем вернуться к рисункам с №4 до №8 из первого раздела этой статьи.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Продифференцируем функцию:
Очевидно, производная существует на всей области определения функции.
Для первого промежутка 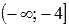
Второй интервал 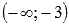
Следовательно, значения функции находятся в интервале 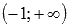
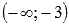
Для интервала (-3;2) воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к двойке слева:
На промежутке 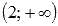
То есть, на этом интервале функция принимает значения из промежутка 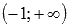
А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.
На этом можно закончить с нахождением наибольшего и наименьшего значения функции. Алгоритмы, разобранные в этой статье, позволяют получить результаты при минимуме действий. Однако бывает полезно сначала определить промежутки возрастания и убывания функции и только после этого делать выводы о наибольшем и наименьшем значении функции на каком-либо интервале. Это дает более ясную картину и строгое обоснование результатов.
Наибольшее и наименьшее значение функции
Теория к заданию 12 из ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
Чтобы найти точки максимума или минимума необходимо:
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^ |
| $<1>/ | $-<1>/ |
| $<1>/x<^n>, n∈N$ | $- |
| $√^n | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | $<1>/ |
| $log_x$ | $<1>/ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
Производная суммы и разности равна производной каждого слагаемого
Как найти наименьшее значение функции на отрезке: правила, примеры и особенности
Исследование функций и их графиков – это тема, которой уделяется особое внимание в рамках школьной программы старших классов. Некоторые основы математического анализа – дифференцирования – включены в профильный уровень экзамена по математике. У некоторых школьников возникают проблемы с этой темой, так как они путают графики функции и производной, а также забывают алгоритмы. В этой статье будут рассмотрены основные типы заданий и способы их решения.
Что такое значение функции?

Математическая функция представляет собой особое уравнение. Оно устанавливает взаимосвязь между числами. Функция зависит от значения аргумента.
Значение функции рассчитывается по заданной формуле. Для этого следует подставить любой аргумент, который соответствует области допустимых значений, в эту формулу на место х и выполнить необходимые математические операции. Какие?
Как можно найти наименьшее значение функции, используя график функции?

Графическое изображение зависимости функции от аргумента называется графиком функции. Он строится на плоскости с определенным единичным отрезком, где по горизонтальной оси абсцисс откладывается значение переменной, или аргумента, а по вертикальной оси ординат – соответствующее ему значение функции.
Чем больше значение аргумента, тем правее он лежит на графике. И чем больше значение самой функции, тем выше находится точка.
О чем это говорит? Самым маленьким значением функции будет являться точка, которая лежит ниже всего на графике. Для того чтобы найти его на отрезке графика, нужно:
1) Найти и отметить концы этого отрезка.
2) Визуально определить, какая точка на этом отрезке лежит ниже всего.
3) В ответ записать ее числовое значение, которое можно определить, спроецировав точку на ось ординат.
Точки экстремума на графике производной. Где искать?
Однако при решении задач иногда дан график не функции, а ее производной. Для того чтобы случайно не допустить глупую ошибку, лучше внимательно читать условия, так как от этого зависит, где нужно искать точки экстремума.
Из этого можно сделать вывод, что в точках экстремума производная лежит на оси абсцисс или обращается в ноль. Но кроме того, в этих точках функция меняет свое направление. То есть после периода возрастания начинает убывать, а производная, соответственно, сменяется с положительной на отрицательную. Или наоборот.
Важно: если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если требуется найти значение функции, то предварительно нужно подставить соответствующее значение аргумента в функцию и рассчитать его.
Как находить точки экстремума с помощью производной?
Рассмотренные примеры в основном относятся к заданию под номером 7 экзамена, которое подразумевает работу с графиком производной или первообразной. А вот задание 12 ЕГЭ – найти наименьшее значение функции на отрезке (иногда – наибольшее) – выполняется без каких-либо чертежей и требует базовых навыков математического анализа.
Для его выполнения нужно уметь находить точки экстремума с помощью производной. Алгоритм их нахождения таков:
Для этого нужно начертить схему и на получившихся промежутках определить знаки производной, подставляя числа, принадлежащие отрезкам, в производную. Если при решении уравнения вы получили корни двойной кратности – это точки перегиба.
Вычисление наименьшего значения функции с применением производной
Однако, выполнив все эти действия, мы найдем значения точек минимума и максимума по оси абсцисс. Но как найти наименьшее значение функции на отрезке?
Что необходимо сделать для того, чтобы найти число, которому соответствует функция в конкретной точке? Нужно подставить в данную формулу значение аргумента.
Точки минимума и максимума соответствуют наименьшему и наибольшему значению функции на отрезке. Значит, чтобы найти значение функции, нужно рассчитать функцию, используя полученные значения х.
Важно! Если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если нужно найти значение функции, то предварительно следует подставить соответствующее значение аргумента в функцию и выполнить необходимые математические операции.
Что делать, если на данном отрезке отсутствуют точки минимума?
Но как найти наименьшее значение функции на отрезке, на котором отсутствуют точки экстремума?
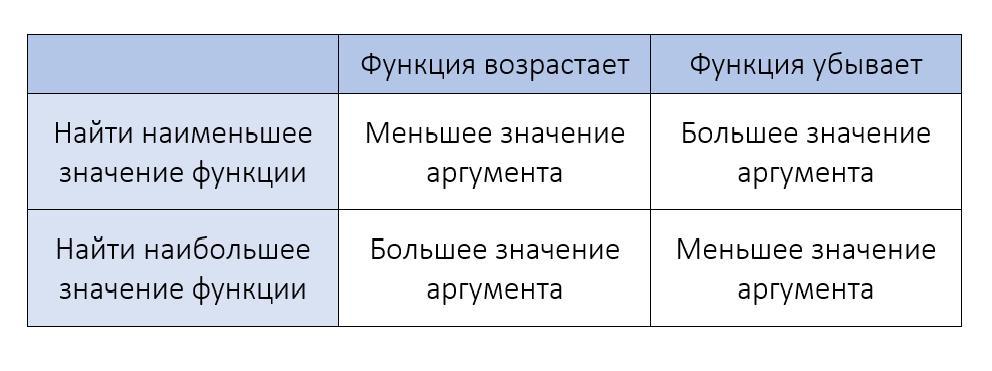
Это значит, что на нем функция монотонно убывает или возрастает. Тогда в функцию нужно подставить значение крайних точек этого отрезка. Есть два пути.
1) Рассчитав производную и промежутки, на которых она положительна или отрицательна, сделать вывод о том, убывает функция на данном отрезке или возрастает.
В соответствии с ними подставить в функцию большее или меньшее значение аргумента.
2) Просто подставить в функцию обе точки и сравнить полученные значения функции.
В каких заданиях нахождение производной необязательно
Как правило, в заданиях ЕГЭ все же нужно находить производную. Есть только пара исключений.
Вершина параболы находится по формуле.
Если a 0, то ветви параболы направлены вверх, вершина – точка минимума.
Рассчитав точку вершины параболы, следует подставить ее значение в функцию и вычислить соответствующее значение функции.
2) Функция y = tg x. Или y = ctg x.
Эти функции являются монотонно возрастающими. Поэтому, чем больше значение аргумента, тем больше значение самой функции. Далее мы рассмотрим, как найти наибольшее и наименьшее значение функции на отрезке с примерами.
Основные типы заданий
Задание: наибольшее или наименьшее значение функции. Пример на графике.
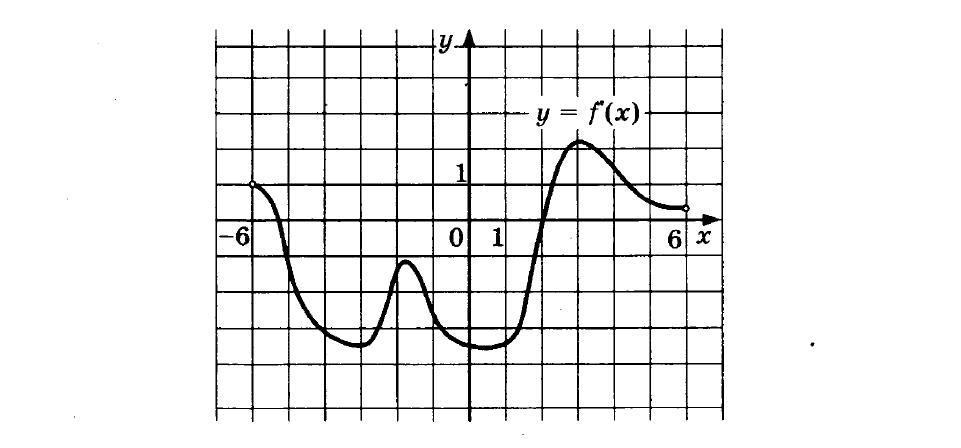
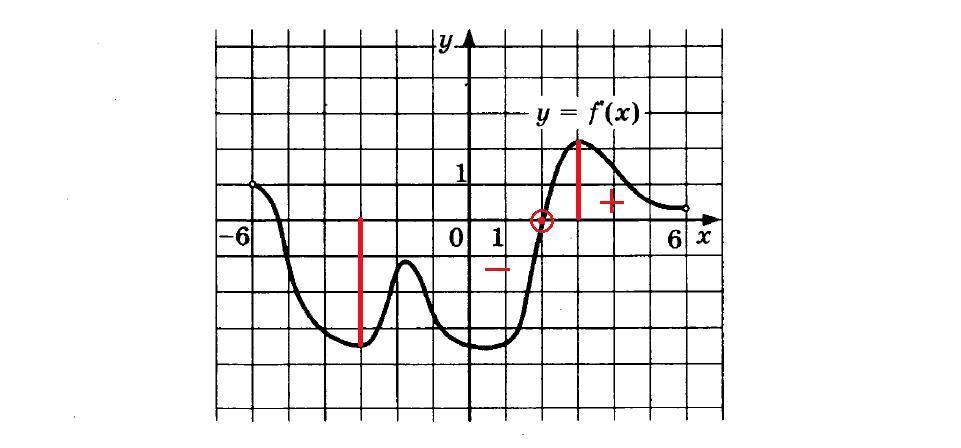
На рисунке вы видите график производной функции f (x) на интервале [-6; 6]. В какой точке отрезка [-3; 3] f (x) принимает наименьшее значение?
Итак, для начала следует выделить указанный отрезок. На нем функция один раз принимает нулевое значение и меняет свой знак – это точка экстремума. Так как производная из отрицательной становится положительной, значит, это точка минимума функции. Этой точке соответствует значение аргумента 2.
Продолжаем рассматривать примеры. Задание: найти наибольшее и наименьшее значение функции на отрезке.
1. Взять производную от сложной функции.
2. Приравнять полученную производную к нулю и решить уравнение.
x = 7; ex-7 ≠ 0, нет корней
3. Подставить в функцию значение крайних точек, а также полученные корни уравнения.
Итак, в этой статье была рассмотрена основная теория о том, как найти наименьшее значение функции на отрезке, необходимая для успешного решения заданий ЕГЭ по профильной математике. Также элементы математического анализа применяются при решении заданий из части С экзамена, но очевидно, они представляют иной уровень сложности, и алгоритмы их решений сложно уместить в рамки одного материала.
Нахождение наибольшего и наименьшего значения функции на отрезке
Наибольшее и наименьшее значение функции — ключевые понятия
Понятие самого большого и самого малого значения производной функции используется для определения оптимального показателя некоторого параметра.
Допустим, X — это некоторое множество, включенное в область определения функции y=f(x).
Наибольшее значение функции y=f(x) на заданном интервале x — это такое максимальное значение y=f(x0) при x∈X, когда неравенство f(x)≤f(x0) справедливо при всех значениях x, принадлежащих X и не равных нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Наименьшее значение функции y=f(x) на заданном интервале x — это такое минимальное значение y=f(x0) при x∈X, когда неравенство f(x)≥f(x0) верно при всех значениях x, принадлежащих X и не равных нулю.
Если упростить данные определения, то получим следующее: максимальное значение функции представляет собой наибольшее значение на известном промежутке при x0, а минимальное — это наименьшее значение, которое принимает функция на известном промежутке при x0.
При обращении производной функции в ноль значения аргумента именуются стационарными точками.
Согласно теореме Ферма, данное понятие представляет собой такую точку, где расположены локальный минимум и максимум дифференцируемой функции или ее экстремум. Отсюда следует, что наименьшее и наибольшее значения y=f(x) будут достигнуты в одной из стационарных точек.
Самое большое и самое маленькое значение функция может принимать в точках, где функция определена, а первой производной данной функции нет.
Наименьшее и наибольшее значения не всегда можно вычислить. К примеру, это невозможно при совпадении рубежей заданного интервала с рубежами области определения. Также максимальные и минимальные значения не получится определить, когда речь идет о бесконечном промежутке.
Кроме того, функция неизвестном отрезке или на бесконечном интервале будет принимать бесконечно малые либо бесконечно большие значения. Это значит, что наименьшее и наибольшее значения в этом случае невозможно рассчитать.
Как найти для отрезка, алгоритм вычисления
Отрезок представляет собой часть прямой, которая ограничена двумя точками. Возьмем точки a и b за концы заданного отрезка. Тогда необходимо найти max y=f(x0) и min y=f(x0) на промежутке [a,b].
Примеры решения задач
Задача 1
Дано: функция, заданная уравнением
Найти max y=f(x0) и min y=f(x0) на промежутке [0,4].
Решение
1. Функция представляет собой кубический многочлен. Точки разрыва отсутствуют, следовательно, функция непрерывна на заданном промежутке [0, 4].
2. Найдем производную:
3. Приравниваем найденную производную к нулю:
4. Решим полученное уравнение и определим критические точки:
5. Проверяем, принадлежат ли данные точки отрезку [0,4]:
6. Поскольку обе критические точки находятся на заданном отрезке, то выполним расчет f(x) для этих точек и для границ промежутка [0,4]:
Среди найденных чисел наибольшее значение равно 170, наименьшее значение \(-7\frac<17><108>\)
Задача 2
Вычислить максимальное и минимальное значение функции на интервале [−4,4]. Функция задана уравнением:
Решение
1. Проверяем функцию на прерывность: f(x) является непрерывной, поскольку при любых x знаменатель не равен нулю.
2. Находим производную:
3. Приравняем образовавшуюся производную к 0 и вычислим крайние точки:
4. Единственная критическая точка лежит в пределах [−4,4].
5. Определим значения функции для x=−4, x=0 и x=4: