наличие какой тенденции во временном ряду свидетельствует о мультипликативной модели временного ряда
Модели временных рядов. Аддитивная и мультипликативная модель
Модели, которые построенны по данным, характеризующим один объект за ряд определенных последовательных периодов, называется моделями временных рядов.
Временной ряд – это совокупность значений определенного показателя за несколько последовательных периодов времени.
Каждый уровень временного ряда может формироваться из трендовой (Т), циклической или сезонной компоненты (S), а также случайной (E) компоненты.
Модели, где временной ряд представлен в виде суммы перечисленных компонентов называются аддитивными, если в виде произведения – мультипликативными моделями.
Аддитивная модель имеет вид: Y = T + S + E
Мультипликативная модель имеет вид: Y = T * S * E
Построение модели временного ряда
Аналитическое выравнивание временного ряда
Построение аналитической функции при моделировании тренда, в любой задаче по эконометрике на временные ряды, называют аналитическим выравниванием временного ряда и в основном применяются функции: линейную, степенную, гиперболичческую, параболическую и т.д.
Параметры тренда определяются как и в случае линейной регрессии методом МНК, где в качестве независимой переменной выступает время, а в качестве зависимой переменной – уровни временного ряда. Критерием отбора наилучшей формы тренда служит наибольшее значение коэффициента детерминации, критерии фишера и Стьюдента.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков за текущий и предыдущие моменты времени. Для определения автокорреляции остатков используется критерий Дарбина – Уотсона:
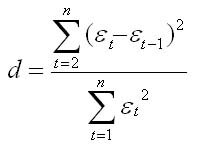
Определение тенденции временного ряда
После того как из исходного временного ряда исключены сезонные колебания, определение тенденции временного ряда осуществляется традиционным способом. Выбирается вид зависимости для тенденции (линейная или нелинейная) и далее методом наименьших квадратов определяются коэффициенты регрессионного уравнения.
Помимо визуального подбора могут применяться и различные аналитические методы.
Прогнозные значения переменной 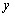
для аддитивной модели 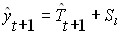
для мультипликативной модели 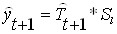
Прогнозирование случайной составляющей
После того как построена прогнозная модель, включающая тенденцию и сезонные колебания необходимо найти и проанализировать остатки 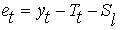
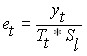
Близость остатков к стационарному временному ряду свидетельствует о том, что кардинальное улучшение прогнозной модели уже не возможно, но, тем не менее, несколько повысить точность прогнозирования возможно за счет прогнозирования самих остатков. Наиболее просто прогнозировать остатки можно двумя способами – с помощью скользящей средней и с помощью экспоненциально взвешенной средней.
При прогнозировании с помощью скользящей средней прогнозное значение остатка (отклонения прогнозного значения 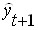
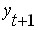
где: 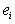
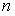
Таким образом, в этом случае используются не центральные скользящие средние, а концевые скользящие средние, т.е. средние, рассчитываемые по текущей точке и n предыдущих точек. Чем меньшее число точек использовано для расчета скользящей средней, тем сильнее прогноз реагирует на последние значения (на последние ошибки).
При прогнозировании с помощью экспоненциально взвешенной средней прогнозное значение остатка определяется не на основании n последних точек, а по всем предшествующим точкам, но в этом случае вес этих точек убывает по экспоненциальной зависимости. Одна из формул для подсчета экспоненциально взвешенной средней имеет вид:
где: 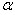
Обычно параметр сглаживания 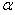
Прогнозирование с помощью скользящей средней и экспоненциально взвешенной средней дают примерно одинаковые результаты, но прогнозирование с помощью экспоненциально взвешенной средней лучше работает в ситуациях когда ряд не до конца стационарен, т.е. нам не удалось учесть в прогнозной модели все тенденции. Как правило прогнозирование с использованием не только тенденции и сезонной составляющей, но и на прогноз остатка позволяет несколько уменьшить дисперсию ошибок прогнозирования. Прогнозные уравнения при этом будут иметь вид:
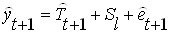
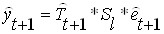
Что такое временной ряд? Чем временной ряд отличается от выборки перекрестных данных? Какие компоненты обычно наблюдаются во временных рядах? Что такое сезонная компонента временного ряда? Почему при моделировании временного ряда необходимо вначале выделить сезонную компоненту? Что такое непериодические колебания и как с ними поступают в тех случаях, когда их невозможно выделить? Чем отличаются аддитивная и мультипликативные модели и как на практике определить какая из моделей больше подходит к прогнозируемому временному ряду Как определить длину периода сезонных колебаний? Что такое межинтервальная скользящая средняя и в каких случаях она возникает? Какому условию должны соответствовать сезонные отклонения в аддитивной модели и как их обеспечить? Какому условию должны соответствовать сезонные отклонения в мультипликативной модели и как их обеспечить? Какие данные используются для определения тенденции временного ряда? Как исключить сезонные колебания из временного ряда? Что такое индекс сезонности? Что такое стационарный временной ряд и как определить насколько близки к нему остатки? Что такое концевая скользящая средняя и для чего она применяется? Что такое экспоненциально взвешенная скользящая средняя и для чего она применяется? Что такое параметр сглаживания и как он влияет на точность прогнозирования? Что дает прогнозирование остатков? Какой из методов прогнозирования остатков более предпочтителен и при каких условиях?
Лекция 6: «ХАРАКТЕРИСТИКИ ВРЕМЕННЫХ РЯДОВ»



Вопрос 1: «ОСНОВНЫЕ ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА»
Можно построить эконометрическую модель, используя два типа исходных данных:
· данные, характеризующие совокупность различных объектов в определенный момент (период) времени;
· данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.
Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называютсямоделями временных рядов.
Временной ряд — это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
· факторы, формирующие тенденцию ряда;
· факторы, формирующие циклические колебания ряда;
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы.
Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию. На рис. 6.1 а) показан гипотетический временной ряд, содержащий возрастающую тенденцию.
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний; уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой-бизнес цикла, в которой находится экономика страны. На рис. 6.1 б) представлен гипотетический временной ряд, содержащий только сезонную компоненту.
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты. Пример ряда, содержащего только случайную компоненту, приведен на рис. 6.1 в).
Очевидно, что реальные данные не следуют целиком и полностью из каких-либо описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача эконометрического исследования от дельного временного ряда — выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов
Рис. 6.1. «Основные компоненты временного ряда: а – возрастающая тенденция; б – сезонная компонента, в – случайная компонента.
Вопрос 2: «АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА И ВЫЯВЛЕНИЕ ЕГО СТРУКТУРЫ»
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называютавтокорреляцией уровней рада.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Рассмотрим пример.
Пример 6.1 Расчет коэффициентов автокорреляции уровней для временного ряда расходов на конечное потребление.
Пусть имеются следующие условные данные о средних расходах на конечное потребление yt (д.е.) за 8 лет. Табл. 6.1
Расчет коэффициента автокорреляции первого порядка для временного ряда расходов на конечное потребление, д.е.
| t |  |  |  |  | (  )* ( )* (  ) ) |  |  |
| 1 | 7 | — | — | — | — | — | — |
| 2 | 8 | 7 | -3,29 | -3,00 | 9,86 | 10,80 | 9,00 |
| 3 | 8 | 8 | -3,29 | -2,00 | 6,57 | 10,80 | 4,00 |
| 4 | 10 | 8 | -1,29 | -2,00 | 2,57 | 1,65 | 4,00 |
| 5 | 11 | 10 | -0,29 | 0,00 | 0,00 | 0,08 | 0,00 |
| 6 | 12 | 11 | 0,71 | 1,00 | 0,71 | 0,51 | 1,00 |
| 7 | 14 | 12 | 2,71 | 2,00 | 5,43 | 7,37 | 4,00 |
| 8 | 16 | 14 | 4,71 | 4,00 | 18,86 | 22,22 | 16,00 |
| Итого | 86 | 70 | 0 | 0 | 44,00 | 53,42857 | 38 |
Расходы на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет.
Определим коэффициент корреляции между рядами 

Одна из рабочих формул для расчета коэффициента корреляции имеет вид:
В качестве переменной х мы рассмотрим ряд 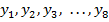

Эту величину называют коэффициентом автокорреляции уровней первого порядка, т.к. он измеряет зависимость между соседними уровнями ряда t и t-1, т.е. при лаге 1.
Для данных пример 6.1 соотноешния (6.2) составят:
Используя формулу (6.1), получаем коэффициент автокорреляции первого порядка:
Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующего годов, и, следовательно, о наличии во временном ряде расходов на конечное потребление сильной линейное тенденции.
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорелляции второго порядка характеризует тесноту связи между уровнями 

Для данных из примера 6.1 получим:
Построим таблицу 6.2 подставив полученные значения в формулу (6.3), имеем:
Расчет коэффициента автокорреляции второго порядка для временного ряда расходов на конечное потребление, д.е.
| t |  |  |  |  |  |  |  |
| 1 | 7 | — | — | — | — | — | — |
| 2 | 8 | — | — | — | — | — | — |
| 3 | 8 | 7 | -3,833 | -2,333 | 8,944 | 14,694 | 5,444 |
| 4 | 10 | 8 | -1,833 | -1,333 | 2,444 | 3,361 | 1,778 |
| 5 | 11 | 8 | -0,833 | -1,333 | 1,111 | 0,694 | 1,778 |
| 6 | 12 | 10 | 0,167 | 0,667 | 0,111 | 0,028 | 0,444 |
| 7 | 14 | 11 | 2,167 | 1,667 | 3,611 | 4,694 | 2,778 |
| 8 | 16 | 12 | 4,167 | 2,667 | 11,111 | 17,361 | 7,111 |
| Итого | 86 | 56 | 0,000 | 0,000 | 27,333 | 40,833 | 19,333 |
Полученные результаты еще раз подтверждают вывод о том, что ряд расходов на конечное потребление содержит линейную тенденцию.
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.
Необходимо отметить два важных свойства коэффициента корреляции.
Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называютавтокорреляционной функцией временного рада. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называетсякоррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка t, ряд содержит циклические колебания с периодичностью в t моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний и имеет структуру, сходную со структурой ряда, изображенного на рис. 6.1 в), либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.
Временной ряд расходов на конечное потребление, рассмотренный нами в примере 6.1, содержит только тенденцию, так как коэффициенты автокорреляции его уровней высокие.
Пример 6.2.Автокорреляционная функция и выявление структуры ряда.
Пусть имеются условные данные об объемах потребления электроэнергии жителями региона за 16 кварталов. (табл. 6.3).
Потребление электроэнергии жителями региона, млн. кВт*ч
| t |  |  |  |  |  |
| 1 | 6,0 | — | — | — | — |
| 2 | 4,4 | 6,0 | — | — | — |
| 3 | 5,0 | 4,4 | 6,0 | — | — |
| 4 | 9,0 | 5,0 | 4,4 | 6,0 | — |
| 5 | 7,2 | 9,0 | 5,0 | 4,4 | 6,0 |
| 6 | 4,8 | 7,2 | 9,0 | 5,0 | 4,4 |
| 7 | 6,0 | 4,8 | 7,2 | 9,0 | 5,0 |
| 8 | 10 | 6,0 | 4,8 | 7,2 | 9,0 |
| 9 | 8,0 | 10 | 6,0 | 4,8 | 7,2 |
| 10 | 5,6 | 8,0 | 10 | 6,0 | 4,8 |
| 11 | 6,4 | 5,6 | 8,0 | 10 | 6,0 |
| 12 | 11,0 | 6,4 | 5,6 | 8,0 | 10 |
| 13 | 9,0 | 11,0 | 6,4 | 5,6 | 8,0 |
| 14 | 6,6 | 9,0 | 11,0 | 6,4 | 5,6 |
| 15 | 7,0 | 6,6 | 9,0 | 11,0 | 6,4 |
| 16 | 10,8 | 7,0 | 6,6 | 9,0 | 11,0 |
Нанесем эти значения на график 6.2
Рис. 6.2. «Потребление электроэнергии жителями региона»
Определим коэффициент автокорреляции первого порядка (добавим 











| Лаг | Коэффициент автокорреляции уровней | Коррелограмма |
| 1 | 0,165154 | ** |
| 2 | -0,566873 | ******* |
| 3 | 0,113558 | * |
| 4 | 0,983025 | ************ |
| 5 | 0,118711 | * |
| 6 | 0,722046 | ********* |
| 7 | 0,003367 | |
| 8 | 0,973848 | ************ |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции, во-вторых, сезонных колебаний периодичностью в четыре квартала. Данный вывод подтверждается и графическим анализом структуры ряда (см. рис. 6.2).
Аналогично, если, например, при анализе временного ряда наиболее высоким оказался коэффициент автокорреляции уровней второго порядка, ряд содержит циклические колебания в два периода времени, т.е. имеет пилообразную структуру.
Вопрос 3: «Моделирование тенденции временного ряда»
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называютаналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:
Линейный тренд
Гипербола: 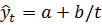
Экспоненциальный тренд:
Тренд в форме степенной функции:
Парабола второго и более высоких порядков:
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t = 1, 2, …, n, а в качестве зависимой переменной — фактические уровни временного ряда уt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни 

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации R 2 и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
Вопрос 4: «Моделирование сезонных и циклических колебаний»
Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (Е) компонент. Общий вид мультипликативной модели выгладит так:
Эта модель предполагает, что каждый уровень временного ряда может бьггь представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+ Е) в аддитивной или (Т*Е) в мультипликативной модели.
4. Аналитическое выравнивание уровней (Т+Е) или (Т*Е) и расчет значений Т с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (Т + S) или (T * S).
6. Расчет абсолютных и/или относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок Е для анализа взаимосвязи исходного ряда и других временных рядов.
Подробнее методику построения каждой из моделей рассмотрим на примерах.
Пример 6.4. Построение аддитивной модели временного ряда.
Обратимся к данным об объеме потребления электроэнергии жителями района за последние четыре года, представленным в табл. 6.3.
В примере 6.2 было показано, что данный временной ряд содержит сезонные колебания периодичностью 4. Объемы потребления электроэнергии в осенне-зимний период времени (I и IV кварталы) выше, чем весной и летом (II иIII кварталы). По графику, этого ряда (рис. 6.2) можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о возможном существовании в ряде аддитивной модели. Рассчитаем ее компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
а. просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 6.5);
б. разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 6.5). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
в. приведем эта значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних — центрированные скользящие средние (гр. 5 табл. 6.5).
Расчет оценок сезонной компонентности в аддитивной модели
| № квартала, t | Потребление электроэнергии,  | Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 6 | — | — | — | — |
| 2 | 4,4 | 24,40 | 6,100 | — | — |
| 3 | 5 | 25,60 | 6,400 | 6,250 | -1,250 |
| 4 | 9 | 26,00 | 6,500 | 6,450 | 2,550 |
| 5 | 7,2 | 27,00 | 6,750 | 6,625 | 0,575 |
| 6 | 4,8 | 28,00 | 7,000 | 6,875 | -2,075 |
| 7 | 6 | 28,80 | 7,200 | 7,100 | -1,100 |
| 8 | 10 | 29,60 | 7,400 | 7,300 | 2,700 |
| 9 | 8 | 30,00 | 7,500 | 7,450 | 0,550 |
| 10 | 5,6 | 31,00 | 7,750 | 7,625 | -2,025 |
| 11 | 6,4 | 32,00 | 8,000 | 7,875 | -1,475 |
| 12 | 11 | 33,00 | 8,250 | 8,125 | 2,875 |
| 13 | 9 | 33,60 | 8,400 | 8,325 | 0,675 |
| 14 | 6,6 | 33,40 | 8,375 | -1,775 | |
| 15 | 7 | ||||
| 16 | 10,8 |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями рада и центрированными скользящими средними (гр. 6 табл. 6.5). Используем эти оценки для расчета значений сезонной компоненты S (табл. 6.6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Расчет значений сезонной компоненты в аддитивной модели
Для данной модели имеем:
Определим корректирующий коэффициент:
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
Проверим условие равенства нулю суммы значений сезонной компоненты:
Таким образом, получены следующие значения сезонной компоненты:
I квартал: 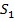
IV квартал: 
Занесем полученные значения в табл. 6.6 для соответствующих кварталов каждого года (стр.3)
Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т+E=Y-S (гр.4 табл. 6.7). Эти значения рассчитываются за каждый период времени и содержат только тенденцию и случайную компоненту.
Расчет выравненных значений Т и ошибок Е в аддитивной модели
| t |  |  |  | T | T+S |  | E 2 |
| 1 | 6,0 | 0,581 | 5,419 | 5,902 | 6,483 | -0,483 | 0,2333 |
| 2 | 4,4 | -1,977 | 6,337 | 6,088 | 4,111 | 0,289 | 0,0835 |
| 3 | 5,0 | -1,294 | 6,294 | 6,275 | 4,981 | 0,019 | 0,0004 |
| 4 | 9,0 | 2,690 | 6,310 | 6,461 | 9,151 | -0,151 | 0,0228 |
| 5 | 7,2 | 0,581 | 6,619 | 6,648 | 7,229 | -0,029 | 0,0008 |
| 6 | 4,8 | -1,977 | 6,777 | 6,834 | 4,857 | -0,057 | 0,0032 |
| 7 | 6,0 | -1,294 | 7,294 | 7,020 | 5,727 | 0,273 | 0,0745 |
| 8 | 10,0 | 2,690 | 7,310 | 7,207 | 9,896 | 0,104 | 0,0108 |
| 9 | 8,0 | 0,581 | 7,419 | 7,393 | 7,974 | 0,026 | 0,0007 |
| 10 | 5,6 | -1,977 | 7,577 | 7,580 | 5,603 | -0,030 | 0,0009 |
| 11 | 6,4 | -1,294 | 7,694 | 7,766 | 6,472 | -0,072 | 0,0052 |
| 12 | 11,0 | 2,690 | 8,310 | 7,952 | 10,642 | 0,358 | 0,1282 |
| 13 | 9,0 | 0,581 | 8,419 | 8,139 | 8,720 | 0,258 | 0,0784 |
| 14 | 6,6 | -1,977 | 8,577 | 8,325 | 6,348 | 0,252 | 0,0635 |
| 15 | 7,0 | -1,294 | 8,294 | 8,519 | 7,218 | -0,218 | 0,0475 |
| 16 | 10,8 | 2,690 | 8,110 | 8,698 | 11,388 | -0,588 | 0,3457 |
Шаг 4. Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (Т+Е) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
Коэффициент регрессии 0,186421
Стандартная ошибка коэффициента регрессии 0,015188
Число наблюдений 16
Число степеней свободы 14
Таким образом, имеем следующий линейный тренд:
Подставляя в это уравнение значения t=1, …, 16, найдем уровни Т для каждого момента времени (гр. 5 табл. 6.7). График уравнения тренда приведен на рис. 6.3.
Рис. 6.3. «Потребление электроэнергии жителями района (фактическое, выравненные и полученные по аддитивной модели значения уровней ряда)
Шаг 5.Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов. Графически значения (Т+S) представлены на рис. 6.3.
Шаг 6. В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле
Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в гр. 7 табл. 6.7.
Следовательно, можно сказать, что аддитивная модель объясняет 98,5% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.
Вопрос 5: «Моделирование тенденции временного ряда при наличии структурных изменений».
От сезонных и циклических колебаний следует отличать единовременные изменения характера тенденции временного ряда, вызванные структурными изменениями в экономике или иными факторами. В этом случае, начиная с некоторого момента времени 
Рис. 6.4. «Изменение характера тенденции временного ряда».
Момент (период) времени 

Если это влияние значимо, то для моделирования тенденции данного временного ряда следует использовать кусочно-линейные модели регрессии, т.е. разделить исходную совокупность на две подсовокупности (до момента времени 


Каждый из описанных выше подходов имеет свои положительные и отрицательные стороны. При построении кусочно-линейной модели происходит снижение остаточной суммы квадратов по сравнению с единым для всей совокупности уравнением тренда. Однако разделение исходной совокупности на две части ведет к потере числа наблюдений, и, следовательно, к снижению числа степеней свободы в кажодм уравнении кусочно-линейной модели. Построение единого для всей совокупности уравнения тренда, напротив, позволяет, сохранить число наблюдений n исходной совокупности, однако остаточная сумма квадратов по этому уравнению будет выше по сравнению с кусочно-линейной модели. Построение единого для всей совокупности уравнения тренда, напротив, позволяет сохранить число наблюдений n исходной совокупности, однако остаточная сумма квадратов по этому уравнению будет выше по сравнению с кусочно-линейной моделью. Очевидно, что выбор одной из двух моделей (кусочно-линейной или единого уравнения тренда) будет зависеть от соотношения между снижением остаточной дисперсии и потерей числа степеней свободы при переходе от единого уравнения регрессии к кусочно-линейной модели.
| № уравнения | Вид уравнения | Число наблюдений в совокупности | Остаточная сумма квадратов | Число параметров в уравнении 1 | Число степеней свободы остаточной дисперсии | ||||||||||||||||
| (1) |  |  |  |  |  | ||||||||||||||||
| (2) |  |  |  |  |  | ||||||||||||||||
| (3) |  |  |  |  |  | ||||||||||||||||
| Месяц, 2010 года | Номинальная начисленная заработная плата в % к соответствующему месяцу предыдущего года (2009г.) |
| Январь | 107,6 |
| Февраль | 109 |
| Март | 112 |
| Апрель | 114,5 |
| Май | 113,3 |
| Июнь | 112,0 |
| Июль | 110,6 |
| Август | 112,4 |
| Сентябрь | 112,5 |
| Октябрь | 112,3 |
Построим график данного временного ряда
Рис. 6.2. Динамика темпов роста номинальной заработной платы за 10 мес. 2010г.
На графике рис. 6.2. заметно наличие возрастающего тренда (тенденции). Возможно существование линейной зависимости.
- наличие какой особенности строения ланцетника указывает на его близость с позвоночными животными
- Наличие кальцинатов в молочной железе что это такое
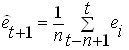

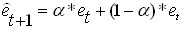




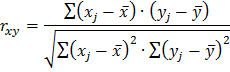






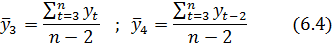

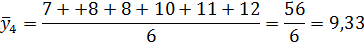











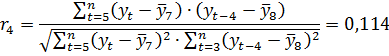


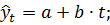






 ) можно найти как сумму
) можно найти как сумму  и
и 


 , с учетом соотношения 6.10 будет равно
, с учетом соотношения 6.10 будет равно

 сравнивают с табличным, полученным по таблицам распределения Фишера для уровня значимости
сравнивают с табличным, полученным по таблицам распределения Фишера для уровня значимости  и числа степеней свободы
и числа степеней свободы 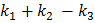 и
и 
