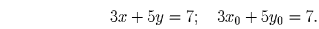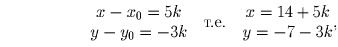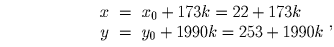найдите сумму x y z где xyz какие нибудь положительные целые числа
Найдите сумму x y z где xyz какие нибудь положительные целые числа
Целые числа x, y и z таковы, что (x – y)(y – z)(z – x) = x + y + z. Докажите, что число x + y + z делится на 27.
Решение
Если числа x, y и z дают различные остатки при делении на 3, то число (x – y)(y – z)(z – x) не делится на 3, а число x + y + z, наоборот, делится на 3. Следовательно, по крайней мере, два из трёх чисел x, y, z дают одинаковые остатки при делении на 3. Но тогда число x + y + z = (x – y)(y – z)(z – x) делится на 3, а для этого необходимо, чтобы и третье число давало тот же остаток при делении на 3, что и первые два числа.
Итак, числа x, y, z дают одинаковые остатки при делении на 3. Значит, число x + y + z = (x – y)(y – z)(z – x) делится на 27.
Замечания
Отметим, что такие числа x, y, z существуют, например, 15, 18 и 21 или 50, 53 и 59.
Источники и прецеденты использования
| олимпиада | |
| Название | Всероссийская олимпиада по математике |
| год | |
| Год | 1993 |
| Этап | |
| Вариант | 5 |
| класс | |
| Класс | 9 |
| задача | |
| Номер | 93.5.9.5 |
| олимпиада | |
| Название | Всероссийская олимпиада по математике |
| год | |
| Год | 1993 |
| Этап | |
| Вариант | 5 |
| класс | |
| Класс | 10 |
| задача | |
| Номер | 93.5.10.5 |
| олимпиада | |
| Название | Московская математическая регата |
| год | |
| Год | 2010/11 |
| Класс | |
| Класс | 10 |
| задача | |
| Номер | 10.3.3 |
Найдите сумму x y z где xyz какие нибудь положительные целые числа
Задача 62:
Решите уравнение 3x + 5y = 7 в целых числах.
Решение:
Найдем сначала какое-нибудь конкретное решение (эта идея, кстати, часто помогает и при решении других задач). Так как 3 2 + 5 ( – 1) = 1, то 3 14 + 5 ( – 7) = 7 и, следовательно, x 0 = 14, y 0 = – 7 – это решение нашего уравнения (одно из многих, не более!). Итак,
Вычтем одно уравнение из другого, обозначим x – x 0 и y – y 0 через a и b, и получим 3a + 5b = 0. Отсюда мы видим, что b делится на 3, а a – на 5. Положим a = 5k, тогда b = – 3k – здесь k, очевидно, может быть любым целым числом. Итак, мы получаем набор решений:
где k может быть любым целым числом. Других решений, конечно, нет.
Задача 63:
Найдите все целые решения уравнения 3x – 12y = 7.
Решение:
Это уравнение не имеет целых решений. Левая часть делится на 3, в то время как правая часть не делится на 3.
Задача 64:
Решите уравнение 1990x – 173y = 11.
Решение:
Числа, участвующие в формулировке, так велики, что подбором здесь конкретного решения не найти. Однако нам поможет то, что числа 1990 и 173 взаимно просты (проверьте это).
Лемма. Их НОД, равный 1, можно представить в виде 1990m – 173n, где m и n – некоторые целые числа.
Доказательство этой леммы следует из того факта, что все числа, которые получаются в процессе алгоритма Евклида, представимы в указанном виде.
k – любое целое число.
Задача 65:
Найдите все целые решения уравнения 21x + 48y = 6.
Решение:
x = 16k – 2, y = – 7k + 1; k – любое целое число.
Задача 66:
Решите уравнение 2x + 3y + 5z = 11 в целых числах.
Решение:
x = 5p + 3q – 11, y = 11 – 5p – 2q, z = p; p, q – любые целые числа.
Задача 67:
Фишка стоит на одном из полей бесконечной в обе стороны клетчатой полоски бумаги. Она может сдвигаться на m полей вправо или на n полей влево. При каких m и n она сможет переместиться в соседнюю справа клетку? За какое наименьшее число ходов она сможет это сделать?
Решение:
При взаимно простых m и n.
Задача 68:
Решение:
( – 4,9), (14, – 21), (4, – 9), ( – 14,21).
Задача 69:
Решение:
Так как xy – x – y = 3, то (x – 1)(y – 1) = 4. Осталось только перебрать возможные разложения числа 4 в произведение двух целых множителей. Ответ: (x = 5,y = 2), (2,5), (0, – 3), ( – 3,0), (3,3), ( – 1, – 1).
Задача 70:
Решение:
Решений в целых числах нет.
Задача 71:
Решение:
(2,0), (2,1), ( – 1,0), ( – 1,1), (0,2), (1,2), (0, – 1), (1, – 1).
Вот как решается задача 69. Так как xy – x – y = 3, то (x – 1)(y – 1) = 4. Осталось только перебрать возможные разложения числа 4 в произведение двух целых множителей. Ответ: (x = 5,y = 2), (2,5), (0, – 3), ( – 3,0), (3,3), ( – 1, – 1).
Задача 72:
В самом деле, посмотрим, какие остатки могут давать точные квадраты по модулю 4 (выбор модуля 4 подсказан нам самим видом правой части уравнения). Недолгий перебор показывает, что это остатки 0 и 1. Так как сумма двух остатков такого вида не может давать остаток – 1, то мы получаем, что решений данное уравнение не имеет.
Задача 73:
Решение:
Решений в целых числах нет (модуль 7).
Задача 74:
Решение:
Так как x³ может по модулю 7 быть сравнимым лишь с 0, 1 и – 1, то выражение x³ + 21y² + 5 сравнимо (mod %)%7 с 5, 6 или с 4, и, следовательно, не может быть равным нулю.
Задача 75:
Решение:
Решений в целых числах нет (модуль 5).
Задача 76:
Решение:
Решений в целых числах нет (модуль 8).
Задача 77:
Решение:
Задача 78:
Решение:
Сразу ясно, что n не делится на 3 и, значит, n = 3k + 1 или n = 3k + 2. Разберем оба случая.
а) n = 3k + 2, 3 2 m + 1 = 9k² + 12k + 4. Сокращая, получаем 2 m = 3k² + 4k + 1 = (3k + 1)(k + 1). Следовательно, и k + 1 и 3k + 1 – степени двойки. Видно, что и k = 0 и k = 1 подходят, и мы получаем решения n = 2, m = 1 и n = 5, m = 3. Но при k ≥ 2 4(k + 1) > 3k + 1 > 2(k + 1) и, следовательно, k + 1 и 3k + 1 не могут одновременно быть степенями двойки.
б) n = 3k + 1. Разбирая этот случай аналогичным образом, мы получаем еще одно решение n = 7, m = 4.
Задача 79:
Решение:
a = b = c = 3; a,b,c = 1,2,3 или 2,4,4; одно из чисел равно 1, а сумма двух других равна 0, например, a = 1, b = – c = 13.
Задача 80:
Решение:
x = ± 498, y = ± 496 или x = ± 78, y = ± 64, причем знаки выбираются независимо.
Задача 81:
Докажите, что уравнение 1/x – 1/y = 1/n имеет единственное решение в натуральных числах тогда и только тогда, когда n – простое число.
Решение:
Если n = pq (p, q > 1), то 1/n = 1/(n – 1) – 1/n(n – 1) и 1/n = 1/p(q – 1) – 1/pq(q – 1). Если же n – простое, то n(y – x) = xy, и значит, xy делится на n, т.е. x или y делится на n. Ясно, что именно y делится на n: y = kn. Тогда x = kn/(n + 1), откуда k = n – 1, т.е. есть ровно одно представление 1/n = 1/(n – 1) – 1/n(n – 1).
Задача 82:
Решите уравнение в целых числах: x³ + 3 = 4y(y + 1).
Задача 83:
Решите уравнение в целых числах: x² + y² = z².
Задача 84:
Решите уравнение в целых числах: x² – 5y² = 1.