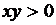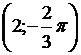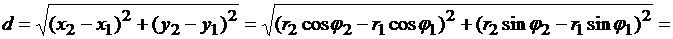Найти сферические координаты точки м зная что луч ом образует с осями
Найти сферические координаты точки

Даны координаты точки (a,b). Найти координаты остальных точек (c,d),(e,j). На рисунке обозначены.
Найти координаты точки
Здравствуйте.Не могу решить задачу. Методом логического размышления пришел к выводу,что вариант.
Найти координаты точки
Добрый вечер, помогите пожалуйста решить пару задач) №1. Найти координаты точки, симметричной.
Найти координаты точки
Добрый день! Есть точка А, образованная 2-мя векторами. Нужно её переместить на длину L, под.

Точка A лежит на прямой x+y=8,причем A равноудаленна от B(2,8) и от прямой x-3y+2=0. Найти.

Точка А лежит на прямой x-y-3=0, 2y+z=0. Расстояние от точки до прямой равно \sqrt<6>. Найти.
Найти координаты точки
Найти координаты точки Т, симметричной точке П (-1;1;1) относительно данной плоскости Г (x+2y+z+4=0)
Найти координаты точки в сфере
Дайте, пожалуйста, формулы для нахождения координаты точки (XYZ) в сфере относительно начала.
Тема 4. Различные системы координат
Полярная система координат


Координатные линии и орты в полярной системе координат
Цилиндрическая система координат
|


Сферическая система координат


Задачи к теме 4
4.1(115). Вычислить расстояние между двумя данными точками:
1) 

2) 

4.2(116*). Даны полярные координаты точек 


4.3(119). Найти площадь треугольника, одна из вершин которого – в полюсе, а две другие имеют полярные координаты 

4.4(121). Зная прямоугольные координаты точек A = (–1, 1), B = (0, 2), C = (5, 0), D = (–8, –6), найти их координаты в полярной системе координат, соответствующей данной прямоугольной.
4.5(123). Полюс полярной системы координат находится в точке (3, 5), а положительное направление полярной оси совпадает с положительным направлением оси Oy. Найти в этой системе полярные координаты точек
M1 = (9, –1) и M2 = (5, 
4.6(124). Найти сферические координаты точек по их прямоугольным координатам: A = (–8, –4, 1), B = (–2, –2, –1), C = (0, –4, 3), D = (1, –1, –1),
E = (0, 1, 0).
4.7(125). Найти сферические координаты точки M, зная, что луч OM образует с осями Ox и Oy углы, соответственно равные 


4.8(126). Найти цилиндрические координаты точек по прямоугольным координатам: A = (3, –4, 5), B = (1, –1, –1), C = (–6, 0, 8).
4.9(130). Найти угол 

1610840688-354d60f870aa4b4d07a90e025d5836ea (Моденов Пархоменко Сборник задач по аналитической геометрии 1976г), страница 5
Описание файла
Просмотр DJVU-файла онлайн
и Р=(6, — ‘); 3) Е=(З’ 18 ) н Е=(4, 9 1′ 116*, Ланы полярные координаты точек А=18, — —
Вычислить выражение (АВ, ВС)+(ВС, СА)+(СА, АВ). 132. В треугольнике АВС даны длины его сторон )ВС(=5, )СА(=6, )АВ
=7. Найти скалярное произведение векторов АВ и ВС. ‘133. В треугольнике АВС проведены медианы А0„ВЕ и СЕ Вычислить (ВС, А0)+(СА, ВЕ)+(АВ, СЕ). 134. Дан прямоугольник АВС0 и точка М (которая может лежать как в плоскости прямоугольника, так и вне ее). Показать, что: 1) (МА, ЛС)=(МВ, Л0); 2) МАа+МС’ = = ЛВа+ Л0а. 135″‘.
В треугольнике АВС точка 0 делит сторону АВ в отношении А0: 0В=Х. Выразить длину отрезка С0 через длины а, Ь, с сторон треугольника и число Х. 136″. Найти сумму векторов, являющихся ортогональными проекниями вектора а на стороны равностороннего треугольника АВС. 137е. Пусть г — радиус окружности, описанной около правильного н-угольника.
Найти: 1) сумму квадратов длин всех сторон и всех диагонзлей этого многоугольника, выходящих из одной его вершины; 2) сумму квадратов длин всех сторон и всех диагоналей этого многоугольника. 138. Докззать, что при любом расположении точек А, В, С, 0 на плоскости или в пространстве имеет место равенство (ВС, А0)+(СА, В0)+(АВ, С0) =О. нэ ] ф У. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 27 139. Доказать, что если в тетраэдре АВС0 два ребра перпендикулярны к противоположным им ребрам, то перпендикулярны и противоположные ребра третьей пары. 140в.
Докззать, что если А, В, С, 0 — четыре произвольные точки (на плоскости или в пространстве), а Р и Π— середины отрезков АС и В0, то (АВ(а+
ВС]а+)С0)Я+)0А(а=! АС(а+(В0)а+4! РО (а. 141*. Даны два вектора а и Ь. Представить вектор Ь в виде суммы двух векторов х и у так, чтобы вектор х был коллинеарен вектору а, а вектор у ортогонален вектору а. 142в. Даны два неколлинеарных вектора а и Ь. Найти вектор х, компланарный векторам а и Ь и удовлетворяющий системе уравнений (а, х)=1, (Ь, х)=0. 143в. Даны три некомпланарных вектора а, Ь, с. Найти вектор х из системы уравнений (а, х)=1, (Ь, х)=0, (с, х)=0. 144*.
Даны два вектора а и Ь. Найти вектор с, являющийся ортогональной проекпией вектора Ь на прямую, направление которой определяется вектором а. 143в. Даны два вектора а и а. Найти вектор Ь, являющийся ортогональной проекпиеи вектора а на плоскость, перпендикулярную к вектору и.
146в. Вычислить длину 1 диагонали 00 параллелепипеда, зная длины ]ОА]=а, (ОВ]=Ь, (ОС]=с трех его ребер, выходящих из одной точки О, и углы х’. ВОС = а,
АОВ=у между ними. Найти также косинусы углов, образуемых диагональю 00 с ребрами ОА, ОВ, ОС. 147. К вершине куба приложены три силы, равные по величине 1, 2, 3 и направленные по диагоналям гранеи куба, выходящим из этой вершины. Найти величину равнодействуюгпей этих трех сил и углы, образуемые ею с состав.
ляющими силами. 148. Найти вектор, являющийся ортогональной проекпиеи вектора ( — 14, 2, 5( на прямую с направляющим вектором (2, — 2, 1(. 149. Найти вектор, являю]нийся ортогональной проекпиеи вектора (8, 4, ]( на плоскость, перпендикулярную к вектору (2, — 2, Ц. 28 ГЛ. 1. ВЕКТОРНАЯ АЛГЕБРА [ 100 150*.
Даны три вектора: а=(8, 4, 1(, Ь=(2, — 2, Ц, с=(1, 1, 9(. Найти вектор, «вляюн[ийся ортогональной проекпией вектора с на плоскость, определяемую векторами а и Ь. 151*. Даны два вектора: а =(8, 4, 1(, Ь=(2, — 2, 1(. Найти вектор с, компланарный векторам а и Ь, перпендикулярный к вектору а, равный ему по длине н образующий с вектором Ь тупой угол. 1б2. Определить внутренние углы треугольника с вершинами А = (1, 2, 3), В =(3, О, 4), С = (2, 1, 3). 153.
Одна из вершин параллелепипеда АВСРА’В’С’Р’ находится в точке А=(1, 2, 3), а копны выходящих из нее ребер — в точках В=(9, 6, 4), Р=(3, О, 4), А’ =(5, 2, 6). Найти длину г[ диагонали АС’ этого параллелепипеда и угол, образуемый АС с ребром АВ. 154. Вычислить углы грт, йь гра, образованные противоположными ребрал1и тетраэдра, першины,которого находятся в точках А=(3, — 1, 0), В=(0, — 7, 3), С=( — 2, 1, — 1), Р=(3, 2, 6), В 8, Векторы на ориентированной плоскости.
Метод координат на плоскости.


|
Проведем через точку А прямую 







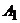
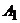
Отметим, что имеет место обще утверждение: точка 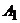
3.1.2. Дана точка А(3;-2). Найти координаты точек, симметричных точке А относительно оси Ох, оси Оу, начала координат.
3.1.3. Найти координаты точки 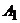
1) второго и четвертого координатных углов;
2) первого и третьего координатных углов.
3.1.4. В треугольнике с вершинами А(2;3), В(6;3), С(6;-5) найти длину биссектрисы ВМ.
Решение: По свойству биссектрисы внутреннего угла треугольника 










М: 
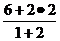


|
т.е. 




Находим длину биссектрисы ВМ: ВМ= 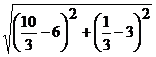


ВМ= 
3.1.5. Доказать, что треугольник с вершинами А(-2;-1), В(6;1),
3.1.6. Точки А(2;4), В(-3;7) и С(-6;6) – три вершины параллелограмма,
причем А и С – противоположные вершины. Найти
3.1.7. Дан треугольник с вершинами А(-2;4), В(-6;8), С(5;-6).
Найти площадь этого треугольника.
3.1.8. Найти точку, в которой прямая, проходящая через точки А(5;5)
и В(1;3), пересечет ось Ох.
Решение: Координаты искомой точки С есть (х;0). А так как точки А, В и С
лежат на одной прямой, то должно выполняться условие

треугольника АВС равна нулю!), где 

точки А, 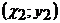

3.1.9. Доказать, что три точки (2;3), (5;7), (11;15) лежат на одной
3.1.10. Разделить отрезок между точками (0;2) и (8;0) в таком же отношении,
в каком находятся расстояния этих точек от начала координат.
3.1.11. На оси ординат найти точку, отстоящую от точки А(3;-8) на
расстоянии 5 единиц.
3.1.12. Найти длину вектора 
угол между этим вектором и положительным направлением оси Ох.
3.1.13. Отрезок с концами А(1;-5) и В(4;3) разделен на три равные части.
Найти координаты точек деления.
3.1.14. Найти координаты центра тяжести однородной пластинки, имеющей
форму треугольника с вершинами в точках А 
3.1.15. Центр тяжести треугольника АВС лежит на оси Ох. Найти координаты вершин С, зная координаты вершин А(3;1) и В(1;-3); площадь треугольника равна 3.
3.1.16. На оси абсцисс найти точку М, расстояние от которой до точки А(1;4) равно 5.
3.1.17. Найти координаты точки, одинаково удаленной от осей координат и от координаты точки А(1;8).
3.1.18. Определить, есть ли среди внутренних углов треугольника с вершинами А(1;1), В(0;2) и С(2;-1) тупой угол.
3.1.19 Даны вершины треугольника: А(7;2), В(1;9), С(-8;-11). Найти расстояние от точки О пересечения медиан треугольника до вершины В.
3.1.20. Две противоположные вершины квадрата находятся в точках А(3;5) и С(1;-3). Найти его площадь.
3.1.21. Найти площадь четырехугольника с вершинами А(-3;2), B(3;4), С(6;1), D(5;-2).
3.1.22. Даны вершины треугольника А(-3;6), В(9;-10), С(-5;4). Найти координаты центра и радиус, описанного около него круга.
3.1.23. Даны вершины А(2;1), В(-2;-2), С(-8;6) треугольника АВС. Найти длину высоты, опущенной из вершины В.
3.1.24. Даны две смежные вершины параллелограмма А(-2;6), В(2;8) и точка пересечения его диагоналей М(2;2). Найти координаты двух других вершин.
3.1.25. Даны середины сторон треугольника М(-1;5), N(1;1), P(4;3). Найти координаты его вершин.
3.1.26. В треугольнике с вершинами О(0;0), А(8;0), В(0;6) определить длины медианы ОС и биссектрисы ОD.
3.1.27. Отрезок с концами А(-8;-8) и В(-2;-4) разделен на 4 равные части. Найти координаты точек деления. До какой точки надо продолжить отрезок АВ, чтобы его длина увеличилась в 3 раза?
3.1.28. Даны точки А(1;2) и В(4;4). На оси Ох найти точку С так, чтобы площадь треугольника АВС была равна 5.
3.1.29. Даны две противоположные вершины квадрата А(3;0) и С(-4;1). Найти координаты двух его других вершин.
3.1.30. Дан треугольник с вершинами А(-√3;1), В(0;2), С(-2√3;2). Найти его внешний угол при вершине А.
3.1.32. Определить центр тяжести однородной пластинки, изображенной на рисунке 8.
 |
3.1.33. Определить площадь параллелограмма, три вершины которого – точки A(-2;3), B(4;-5), C(-3;1).
3.1.34. В точках М1(х1;у1), М2(х2;у2), М3(х3;у3) помещены массы m1, m2, m3 соответственно. Найти центр тяжести системы. Указание, центр тяжести системы двух масс делит отрезок на части, обратно пропорциональные массам, сосредоточенным на концах отрезка.
3.1.35. Найти положение центра тяжести проволочного треугольника, вершины которого расположены в точках (0;0), (0;3) и (4;0).
3.1.36. Даны вершины однородной треугольной пластинки А (х1;у1), В (х2;у2), С (х3;у3). Если соединить середины ее сторон, то образуется новая треугольная пластинка. Доказать, что центры тяжести обеих пластинок совпадают.
3.1.37. Даны две смежные вершины квадрата А (2;-1) и В (-1;3). Найти координаты двух его других вершин.
3.1.38. Найти координаты центра правильного шестиугольника, зная две его смежные вершины: А(2;0) и В(5;3 
3.1.39. Показать, что точки А(-3;8), В(1;5) и С(4;1) могут служить тремя вершинами ромба, вычислить площадь этого ромба.
3.1.40. Прямая линия отсекает на оси Ох отрезок ОА=4 и на оси Оу отрезок ОВ=7. Найти координаты основания перпендикуляра, опущенного из начала координат на данную прямую.
Указание.
3.1.41 В каких четвертях могут быть расположены точки 

2)
3)
4)
5) 
3.1.42. Проведем отрезок от точки А(1;-1) до точки (-4;5). Найти координаты точки, до которой нужно продлить его в том же направлении, чтобы длина его удвоилась?
3.1.43. Доказать, что во всяком прямоугольном треугольнике длина медианы,
соединяющей вершину прямого угла с серединой гипотенузы, равна
3.1.44. Точки А(х1;у1) и В(х2;у2) служат смежными вершинами ромба, диагонали
которого параллельны осям координат. Как выразить координаты остальных вершин через координаты данных точек?
3.1.45. Как расположены точки, имеющие одну и ту же проекцию на ось Ох? на ось Оу?
3.1.46. Найти прямоугольные координаты точки М с полярными координатами
Решение: Имеем 


3.1.47. Найти прямоугольные координаты точек А, В, С, D, E для которых известны полярные координаты А(3;0), 
3.1.48. Найти полярные координаты точки М с прямоугольными координатами 
Решение: Имеем 



3.1.49. Найти полярные координаты точек A, B, C, D, E для которых известны прямоугольные координаты: A(-3;3), B(0;-5), C(-2;-2), D(-4;0), E( 
3.1.50. В полярной системе координат заданы точки M1 ( 
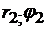
а) расстояние между точками M1 и M2;
б) площадь треугольника OM1M2 (O – полюс).
т.е. 

б) пользуясь формулой для площади треугольника со сторонами a и b и углом 

3.1.51. Сторона правильного шестиугольника равна 1. Приняв за полюс одну из его вершин, а за полярную ось – сторону, через нее проходящую, найти полярные координаты остальных пяти вершин.
3.1.52. В полярной системе координат точка пересечения диагоналей параллелограмма ABCD совпадает с полюсом. Зная вершины 

3.1.53. В полярной системе координат даны две противоположные вершины квадрата 

3.1.54. Одна из вершин треугольника лежит в полюсе полярной системы координат, а другие в точках A(2;0) и 
3.1.55. В полярной системе координат даны точки 


3.1.61. Составить управление линии, точки которой равноотстоят от двух заданных точек А(-2;0) и В(4;2).
3.1.62. Найти геометрическое место точек, одинаково удаленных от прямой х=2 и точки F(4;0).
3.1.63. Стержень АВ скользит своими концами по координатным осям. Точка М делит стержень на две части АМ=a и ВМ=b. Найти параметрические управления траектории точки М, приняв в качестве параметра угол 
Решение: Рассмотрим треугольник МСВ (рис.9): в нем 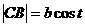



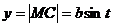






 |
|
Уравнение траектории точки М можно записать виде F(х;у)=0. Для этого перепишем найденные уравнения линии в виде 

 |
|
|
|
|
|
Линия, определяемая этим уравнением, называется эллипсом.
3.1.64. Составить уравнение линии, для каждой точки которой расстояние до оси Ох в три раза меньше, чем до оси Оу.
3.1.65. Найти уравнение траектории перемещения точки М, которая движется так, что расстояние от неё до точки всегда равно 5.


 | |
|
|


в нем |ОМ| = r, 2 +у 2 = 9. Лежат ли на ней точки М1 ( 2√2;1), М2 (2;3)? Пересекается ли эта окружность с прямой у = 3?
Решение: подставляем координаты точки М1 в уравнение окружности. Получаем тождество (2√2) 2 + 1 = 9. Значит, точка М1 лежит на окружности. Точка М2 не лежит на окружности, так как 2 2 + 3 2 

Для ответа на второй вопрос решим систему
откуда получаем х = 0 и у = 3. таким образом, окружность и прямая имеют одну общую точку (0;3) – прямая касается окружности.
3.1.72. Найти точки пересечения кривой у = 6+5х-х 2 с осями координат.
3.1.73. Найти точки пересечения линий х + 7у = 25 и х 2 + у 2 =25.
3.1.74. На окружности х 2 +у 2 =25 найти точки:
3.1.75.В прямоугольных координатах даны параметрические уравнения кривых
а) 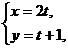
б) 

в) 

Найти уравнения заданных кривых в виде F(x;y)=0
3.1.76. Написать уравнение кривой, сумма расстояний от каждой точки которой до точек F1(-2;0)и F2(2;0) равна 2 
3.1.77. Вывести уравнение геометрического места точек, для которых модуль разности расстояний до точек F1(-4;0) и F2(4;0) равен 4.
Прямая на плоскости.
3.2.1. Записать уравнение прямой у=2х-3 в отрезках и построить ее.
а)параллельна оси Ох;
б) проходит через начало координат.
3.2.3. Найти k из условия, что прямая у=kх+2 удалена от начала координат на расстояние 
3.2.4. Написать уравнение прямой, проходящей через точку А 
3.2.5. Уравнение прямой 4х-3у+12=0 представить в различных видах (с угловым коэффициентом, в отрезках, в виде нормального уравнения).
Решение: Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно у. Получим 3у=4х+12 и далее у 







т.е. расстояние от О(0;0) до прямой равно 2,4.
3.2.6. Записать уравнение с угловым коэффициентом, в отрезках и нормальное для заданных прямых и определить на каком расстоянии от начала координат они находятся:
3.2.7. Написать уравнение прямой, проходящей через точки:

Решение: а) Используем уравнение:
Полагая в нем х 


у 

или 
или 
б) Решаем аналогично: 




3.2.8. Найти угловой коэффициент к прямой и ординату точки ее пересечения с осью Оу, зная, что прямая проходит через точки А(21;1),В(-2;1).
3.2.9 Прямая проходит через точки А(2;3),В(-4;-1), пересекает ось Оу в точке С. Найти координаты точки С.
3.2.10. Какую абсциссу имеет точка М, лежащая на прямой, проходящей через точки А(-2;-2), В(-1;6), и имеющая ординату, равную 22?
3.2.11 Из пучка прямых, определяемых уравнением y+3=k(x-2)
выделить ту, которая проходит через точку А(-2;5)
Решение: Поставим координат точки А в уравнении прямой:
уравнение прямой есть у+3=-2(х-2), т.е. 2х+у-1=0
3.2.12. Найти уравнение прямой:
б)параллельной оси Ох и отсекающей на оси Оу отрезок, равный 2;
в) отсекающей на осях координат отрезки, равные 3 и 4.
3.2.13. Составить уравнение прямой, если точка М (4; 2) является серединой ее отрезка, заключенного между осями координат.
3.2.14. Составить уравнение прямой, отсекающей на положительных полуосях координат равные отрезки, если длина отрезка, заключенного между осями координат, равна 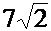
3.2.15. Луч света, пройдя через точку А (2; 3) под углом 

3.2.16. Луч света направлен по прямой х-у-1=0. Определить точку встречи луча с осью Ох и уравнение прямой, по которой направлен отраженный луч.
3.2.17. При каких значениях 




3.2.18. Составить уравнение прямой, проходящей через точку А(4;4) и отсекающей от координатного угла треугольник площадью S = 4.
3.2.19. Составить уравнение биссектрисы внутреннего угла А треугольника АВС с вершинами А(1;-2), В(5;4), С(-2;0).
3.2.20. Составить уравнение прямой, проходящей через точку А(3;-4), являющуюся основанием перпендикуляра, опущенного из начала координат на прямую.
3.2.21. Дан треугольник с вершинами А(3;2), В(3;8), С(6;2). Написать уравнение сторон треугольника.
3.2.22. Составить уравнение прямой, зная, что расстояние от нее до начала координат равно 


3.2.23. Найти площадь треугольника, заключенного между осями координат и прямой
3.2.24. Составить (в полярных координатах) уравнение прямой, проходящей через точки 
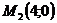
3.2.26. Через середину отрезка АВ, где А(4; 0), В(0;6), провести прямую, отсекающую на оси Ох отрезок вдвое больший, чем на оси Оу и написать ее уравнение.
3.2.27. Написать уравнение прямой, параллельной биссектрисе второго координатного угла и отсекающей на оси Оу отрезок, равный 3.
3.2.28. При каком значении С прямая 2х-3у+С=0 пересекает ось Оу в точках с ординатами 
3.2.29. Написать уравнение прямой, проходящей через точку А(2;-1) и параллельной биссектрисе второго координатного угла.
3.2.30. Найти прямую, проходящую через точку пересечения прямых х-2у+3=0 и 2х+у+5=0 и параллельную оси ординат и написать ее уравнения.
3.2.31. Через точку пересечения прямых х+у-6=0 и 2х+у-13=0 провести прямую (несовпадающую с данными), отсекающую на осях равные отрезки и написать ее уравнение.
3.2.32. Составить уравнение прямой, которая проходит через точку М(2;-6) и отсекает на осях Ох и Оу отрезки одинаковой длины( считая каждый отрезок направленным на начала координат).
3.2.33. Через точку М(4;3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3. Найти точки пересечения этой прямой с осями координат.
3.3.34. Найти угол между прямыми:
1) y=2x-3 и y= 
3) y= 
1) Воспользуемся формулой: tg 
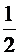




По формуле : tg 
tg φ = 
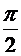
4) к1 = 5, к2 = 5, tg φ = 0, φ = 0.
3.2.35. Найти угол между двумя прямыми:
1)3х+2у – 1 = 0 и 5х –у + 4=0
4) 3х-2у+0,1=0 и 2х+3у-5=0
3.2.36. Найти угол между прямыми:
б) 2х-3у=0 и прямой, проходящей через точки (5;0) и (0;3).
3.2.37. Исследовать взаимное расположение следующих пар прямых:
1) 3х+5у-9=0 и 10х-6у+4=0
5) 
10) 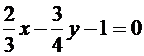

3.2.38. При каких значениях α следующие пары прямых: а)паралленльны; б) перпендикурярны?
1)2х – 3у +4 = 0 и αх – 6у + 7 = 0;
3.2.39. Через точку пересечения прямых 3х-2у+5=0, х+2у-9=0 проведена прямая, параллельная прямой 2х+у+6=0. Составить ее уравнение.
Решение: Найдем сначала точку М пересечения данных прямых. Для этого решим систему уравнений:
Отсюда 4х=4. и далее, х=1, у=4, т.е М(1;4). Угловой коэффициент прямой 2х+у-6=0 есть к1=-2. следовательно, угловой коэффициент к=-2. По направлению прямой (к=-2) и точке М(1;4), ей принадлежащей, запишем уравнение искомой прямой: у-4=-2(х-1), т.е. 2х+у-6=0
3.2.40. Найти уравнение прямой, проходящей через точку А(-1;2):
а) параллельно прямой у=2х-7;
б) перпендикулярно прямой х+3у-2=0
3.2.41. Найти уравнение прямой, проходящей через точку В(2;-3):
а) параллельно прямой, соединяющей точки М1(-4;0) и М2(2;2);
б) перпендикулярно прямой х-у=0
3.2.42 Показать, что уравнение прямой, проходящей через точку (х0;у0), и параллельной прямой Ах+Ву+С=0, имеет вид А(х-х0)+В(у-у0)=0.
3.2.43. Показать, что уравнение прямой. проходящей через точку Ах+Ву+С=0, имеет вид А(х-х0)-В(у-у0)=0.
3.2.44. Найти координаты точки М2, симметричной точке М1 (-3;4), относительно прямой 4х-у- 1=0.
|
Решение: Точки М1и М2 лежат на прямой М1,М2, перпендикулярно прямой 4х-у-1=0, и одинаково удалены от (см.рис. 12, прямая 1). Найдем уравнение прямой М1М2. Так как

равенствами 
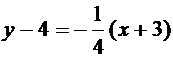
Отсюда x=1, y=3,т.е. М(1;3). Точка М(1;3) делит отрезок М1М2 пополам. Из соотношений 
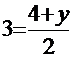
3.2.45 Точка А(2;-5) является вершиной квадрата, одна из сторон которого лежит на прямой x-2y-7=0. Найти площадь этого квадрата.
3.2.46 Две стороны квадрата лежат на прямых 5x-12y-65=0 и 5x-12y+26=0. Найти площадь этого квадрата.
3.2.47 Найти уравнение прямой, проходящей через точку A (1;2) так, чтобы расстояние от этой прямой до точек М1 (2;3) и М2 (4;-5) были бы равны.
3.2.48 Найти геометрическое место точек, расстояние от которых до прямой 5x-12y-13=0 равно 3.
3.2.50 Найти расстояние между параллельными прямыми 3х+4у-20=0 и 6х+8у+5=0
Решение: Возьмем на первой прямой произвольную точку А. Пусть например, х=0, тогда у=5, т.е. А(0;5). Находим расстояние d от точки А до второй прямой:
3.2.51 Найти расстояние между прямыми 2х-3у+8=0 и 4х-6у=10.
3.3.52 Найти длину высоту BD в треугольнике с вершинами А(4;-3), В(-2;6) и С(5;4)
3.2.54 Написать уравнение прямой, проходящей через точку А (1;5) на расстоянии пяти единиц от начала координат.
3.2.55 Найти координаты точки, равноудаленной от двух точек (5;4) и (-3;20 и лежащей на прямой х – 3у + 8 = 0.
3.2.56 Даны две вершины треугольника А (2;-2), В(-6;2) и точка О(1;2) пересечения ее высот. Найти координаты третьей вершины С.
3.2.57 Составить уравнения прямой, содержащей высоту BD в треугольнике с вершинами А(-3;2), В (5;-2), C (0;4).
3.2.58 Найти координаты проекций точки А(1;-3) на прямую 2х – у + 5 = 0.
3.2.59 Найти координаты точки, симметричной точке А(-2;2)относительно прямой х + у = 0.
Смешанные задачи на прямую.
3.2.60 Найти площадь треугольника, образованного прямыми:2х + у + 4 = 0, х + 7у – 11 =0 и 3х – 5у – 7 = 0.
3.2.61 Составить уравнение прямой, проходящей через точку А (-2;1):
а)параллельно оси Оу;
б)образующей с осью Ох угол 
в)перпендикулярно вектору ά = (4;2);
г)параллельно биссектрисе первого координатного угла;
д)перпендикулярно прямой 6х – у + 2 = 0;
е)отсекающей от оси Оу отрезок длиной 5.
3.2.62. Через точку пересечения прямых 3х + 2у – 4 =0 и х – 5у + 8 =0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ох. Составить их уравнения.
3.2.63. Какой угол образует с осью Ох прямая, проходящая через точку D(1;3) и точку пересечения медиан треугольника с вершинами А9-1;4), В (2;3), С(5;8)?
3.2.64. Дан четырехугольник АВСD с вершинами А(3;5), В(6;6), С(5;3), D(1;1). Найти:
а) координаты точки пересечения диагоналей;
б) угол между диагоналями.
3.2.65. Луч света, пройдя через точки А(4;6) и В(5;8), упал на прямую х-2у+2=0 и отразился от нее. Составить уравнения прямой, по которой направлен отраженный луч.
3.2.66. Известны вершины треугольника А(-2;-4), В(0;1), С(2;-1). Найти расстояние от начала координат до точки пересечения медианы, проведенной из вершина В.
3.2.67. Написать уравнения прямых, на которых лежат стороны треугольника АВС, если задана его вершина А(1;3) и уравнения медиан х-2у+1=0 и у-1=0.
3.2.68. Найти координаты основания перпендикуляра, опущенного из точки А(-1;2) на прямую 3х-5у-21=0.
3.2.69. Дан треугольник с вершинами в точках А(2;5), В(5;-1), С(8;3). составить уравнение прямой, проходящей через точку пересечения медиан треугольника перпендикулярно к прямой х+у+4=0.
3.2.70. Известны уравнения прямых, на которых лежат две стороны ромба: х+2у-4=0, х+2у-10=0 и уравнение одного из его диагоналей х-у+2=0. Найти координаты вершин ромба.
3.2.71. Дан треугольник с вершинами в точках А(1;-2), В(0;5), С(-6;5). Найти координаты центра описанной около треугольника окружности.
3.2.72. Даны две вершины равностороннего треугольника АВС: А(-6;0), В(0;0). Найти координаты:
а) третьей вершины С;
б) центра вписанной в треугольник окружности.
3.2.73. Найти уравнения прямых, на которых лежат три стороны квадрата, зная, зная, что четвертой стороной является отрезок прямой 4х+3у-12=0, концы которого лежат на осях координат.
3.2.74. Написать уравнение траектории движения точки М(х;у), движущейся так, что сумма расстояний от нее до прямых 2х-у=0 и х+2у=0 остается постоянной и равно 
3.2.75. Написать уравнения прямых, на котор
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.