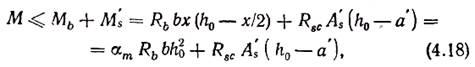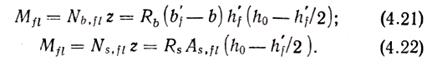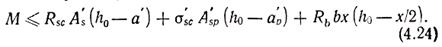назовите число расчетных сечений элементов работающих на изгиб и какой командой оно вводится
Расчет изгибаемых элементов
К изгибаемым элементам относят балки покрытий, перекрытий. рабочих площадок, мостов, эстакад, затворов и др
Изгибаемые элементы рассчитывают по первой группе предельных состояний, когда проверяют их прочность и устойчивость, и по второй группе предельных состояний, когда проверяют их жесткость (прогиб). Расчеты на прочность и устойчивость ведут по расчетным нагрузкам, а расчет на прогиб — по нормативным.
Прочность изгибаемых элементов проверяют по нормальным касательным и приведенным напряжениям. Если балка работает на изгиб в одной из главных плоскостей (рисунок ниже, слева) в пределах упругости, то в сечениях балки получается треугольная эпюра нормальных напряжений (рисунок ниже, справа).
Работа балки на изгиб
а — расчетная схема и эпюры моментов и поперечных сил; б— поперечное сечение и эпюры нормальных и касательных напряжений
Максимальное значение этих напряжений в крайних волокнах
где М—расчетный изгибающий момент; Wnmin — наименьшее значение момента сопротивления с учетом ослаблений.
Касательные напряжения в изгибаемых элементах проверяют в местах наибольшей поперечной силы Q но формуле
где Q — расчетная поперечная сила; Sx — статический момент сдвигаемой части сечения относительно нейтральной оси; Jx — момент инерции (брутто) всего поперечного сечения балки; tω — толщина элемента в месте, где проверяют касательные напряжения (обычно толщина стенки по нейтральному слою); Rs ≈ 0,58Ry — расчетное сопротивление стали на сдвиг.
При ослаблении стенки балки отверстиями для болтов значения τ в формуле ниже следует умножать на коэффициент:
Здесь а — шаг отверстия; d — диаметр отверстий.
Для стенок балок, рассчитываемых по формуле выше делают проверку по приведенным напряжениям с учетом совместного действия нормальных и касательных напряжений. В металлических конструкциях эту проверку производят по энергетической теории прочности.
где σх = M / J n x · y — нормальные напряжения в срединной плоскости стенки, параллельные оcи балки; σy. — то же, перпендикулярные оси балки, в том числе σloc, определяемое по формуле выше;
Общую устойчивость изгибаемых элементов проверяют по первой группе предельных состояний.
Под влиянием нагрузки, расположенной в плоскости одной из главных осей инерции поперечного сечения, балка изгибается в этой плоскости лишь до достижения нагрузкой некоторого критического значения. Затем балка выходит из плоскости изгиба и начинает закручиваться. Это явление называют потерей общей устойчивости балки, а соответствующий ему изгибающий момент — критическим моментом. Форму потери общей устойчивости балки называют изгибно-крутильной (рисунок ниже). В поясах потерявшей устойчивость балки развиваются пластические деформации, и она быстро теряет несущую способность при нагрузке, незначительно превосходящей критическую.
Потеря общей устойчивости консольной двутавровой балки (а) и влияние места приложения нагрузки (б)
Проверка общей устойчивости сводится к сравнению возникающих напряжений с критическими: σ=M/W
Расчет прочности изгибаемых элементов по нормальным сечениям
Рис.3.1. Напряженное состояние и схемы разрушения железобетонной балки:
а – эпюра изгибающих моментов и поперечных сил; б – траектории главных растяги-
вающих напряжений и схема образования трещин; в – схема возможного разрушения
балки; г – сечение с одиночной арматурой; д – сечение с двойным армированием;
1 – продольная арматура; 2 – отгибы; 3 – хомуты; 4 – монтажная арматура
прочность бетона на растяжение, образуется трещина по нормали к продольной оси балки, затем в работу по восприятию момента вступит арматура, а при дальнейшем увеличении нагрузки произойдет разрыв арматуры и балка разрушится. Из этого следует, что необходимо проверять прочность железобетонной балки по нормальному сечению на действие изгибающего момента. На участках между опорами и точками приложения сил, благодаря действию поперечной силы при увеличении нагрузки будут образовываться косые трещины, и разрушение балки может произойти по этой наклонной трещине. Следовательно, при действии поперечных сил требуется проверка прочности железобетонного изгибаемого элемента по наклонному сечению.
Рассмотрим сначаламетод расчета прочности изгибаемых железобетонных элементов по нормальным сечениям. Ранее уже отмечалось, что напряженное состояние балки в нормальном сечении при увеличении нагрузки проходит через несколько характерных стадий (рис.3.2).
На первой стадии, напряжения в бетоне невелики и деформации бетона носят упругий характер. Зависимость между деформациями и напряжениями выражается практически прямой линией и эпюры напряжений в сжатой и растянутой зонах можно считать треугольными. При дальнейшем увеличении нагрузки эпюра напряжений в растянутой зоне приобретает криволинейный характер и напряжения приближаются к напряжениям образования трещин.
Рис.3.2. Стадии напряжено деформированного состояния сечения
железобетонной балки при изгибе
На второй стадии происходит появление и раскрытие трещины в растянутой зоне бетона. Вследствие появления трещины, растягивающие напряжения начинает воспринимать арматура. Напряжения в бетоне сжатой зоны не превышают временного сопротивления бетона сжатию. При дальнейшем увеличении нагрузки в сжатом бетоне возникают неупругие деформации, и эпюра сжимающих напряжений приобретает криволинейный характер. Конец второй стадии характеризуется появлением неупругих деформаций в арматуре.
Третья стадия характеризуется предельным состоянием сечения по прочности. При увеличении нагрузки напряжения в арматуре достигают предела текучести и, следовательно, деформации арматуры происходят при постоянной величине нагрузки. При этом, трещина развивается в направлении верхней грани сечения, высота сжатой зоны уменьшается, а напряжения в сжатом бетоне растут и достигают временного сопротивления бетона при сжатии. Это напряженное состояние называется пластическим шарниром и разрушение элемента происходит с пластическими деформациями и не является хрупким. Такое разрушение принято называть исчерпанием несущей способности по первому случаю. Возможен, однако, и другой сценарий разрушения. Если увеличить площадь поперечного сечения растянутой рабочей арматуры, то ее несущая способность может оказаться выше несущей способности сжатой зоны бетона. В этом случае сжатая зона бетона разрушится раньше того, чем напряжения в арматуре достигнут предела текучести, такое разрушение будет хрупким и называется разрушением по второму случаю. Наиболее рациональным способом проектирования железобетонных сечений считается тот при котором одновременно достигается прочность как по арматуре, так и по сжатому бетону, т.е. разрушение происходит по пограничной зоне между первым и вторым случаем. При расчетах в этой стадии криволинейная эпюра напряжений в сжатом бетоне заменяется на прямоугольную, что как показывает экспериментальная проверка, вносит погрешность не более 2%.
Три стадии напряженного состояния являются основой расчета железобетонных изгибаемых элементов. По первой стадии определяется момент образования трещин, по второй рассчитывается ширина раскрытия трещин, по третьей – выполняется проверка прочности сечений.
Прежде чем перейти к расчету нормального сечения вспомним некоторые сведения из курса «Инженерные конструкции», относящиеся к расчетным и нормативным характеристикам материалов. Для бетона, материала обладающего силовой анизотропией, вводятся два различных нормативных сопротивления Rbn– сопротивление осевому сжатию (призменная прочность) и Rbtn– сопротивление осевому растяжению. Для арматуры в качестве нормативного сопротивления Rsn принимаются наименьшие контролируемые значения предела текучести, физического или условного, за исключением обыкновенной арматурной проволоки класса В240. Для этой арматуры в качестве нормативного сопротивления принимается величина равная 75% временного сопротивления разрыву. Расчетные сопротивления материалов для предельных состояний получаются делением нормативных сопротивлений на коэффициенты надежности по материалу γm. Для бетона это будут коэффициенты надежности при сжатии γbcи при растяжении γbt. Для стали коэффициент надежности по материалу обозначается символом γs.
Расчетные сопротивления бетона для предельных состояний первой группы Rbи Rbtснижаются или повышаются путем умножения на коэффициенты условий работы γbi, учитывающие особенности бетона, длительность действия нагрузок и их цикличность, условия и стадию работы конструкции, способы изготовления конструкции, размеры поперечного сечения и др. Расчетные сопротивления бетона для предельных состояний второй группы, за исключением случая образования трещины по наклонному сечению, вводятся в расчет с коэффициентом надежности по материалу γbс = γbt = 1.
Расчетные сопротивления арматуры Rs для предельных состояний первой группы снижаются или повышаются путем умножения на коэффициенты условий работы γsi, которые учитывают: опасность усталостного разрушения, неравномерность распределения напряжений в сечении, условия анкеровки, прочность бетона и др. Расчетное сопротивление арматуры при расчете по второй группе предельных состояний всегда принимается при коэффициенте надежности по материалу γs = 1.
Итак, прочность изгибаемого железобетонного элемента по нормальному сечению рассчитывается по третьей стадии. Условие прочности сечения записывается следующим образом
Из этого уравнения вычисляется высота сжатой зоны бетона, величина xявляется единственным неизвестным
Рис. 3.3. Схема усилий в нормальном сечении изгибаемого
элемента с одиночной арматурой в стадии предельгого равновесия.
или относительно центра тяжести бетона сжатой зоны
где: Zb = h0 – 0,5 x— плечо внутренней пары сил; h0 = h – a– рабочая высота сечения;
a – расстояние от центра тяжести растянутой арматуры до грани сечения.
ξ = x / h0, (3.6)
Граничная высота сжатой зоны бетона ξRпри которой не происходит его преждевременного хрупкого разрушения определяется по эмпирической формуле
где: ω – характеристика сжатой зоны, для тяжелого бетона ω = 0,85 – 0,0008 Rb;
Если относительная высота сжатой зоны бетона меньше или равна граничной, разрушение произойдет по первому случаю, в противном случае наоборот. Поскольку всегда желательно конструировать элемент так, чтобы возможное разрушение начиналось с текучести арматуры, то необходимо стремиться к тому, чтобы относительная высота сжатой зоны бетона была бы меньше или равна ее граничному значению, т.е. чтобы выполнялось условие
ξ ≤ ξR. (3.8) Если это условие не выполняется, необходимо либо перейти к более прочному бетону, либо увеличить высоту сечения. Далее, если в поставленной ранее задаче неизвестна также площадь поперечного сечения арматурыAs , ее значение можно получить из решения системы двух уравнений (3.2) и (3.4) или (3.5), в которых момент внутренних сил в сечении принимается равным действующему изгибающему моменту Mсеч = М. Разрешая эту систему относительно x, получим
а затем, из соотношения (3.2) можно определить и As. Если сразу искать величину As, получим соотношение
Если при этом, нарушается условие (3.8), то необходимо увеличить высоту сечения hили укрепить сжатую зону бетона и повторить расчет. Таким образом, мы подошли к решению более сложной задачи – задачи прямого проектирования, когда необходимо подобрать площадь сечения растянутой арматуры и габариты сечения. В этой задаче четыре неизвестных: высота сечения h, его ширина, b высота сжатой зоны хи площадь поперечного сечения растянутой арматуры As. Так как, при рассмотрении равновесия сечения имеется всего два уравнения равновесия, двумя из неизвестных величин необходимо задаться.
Из опыта проектирования известно, что наиболее экономичные решения достигаются тогда, когда относительная высота сжатой зоны находится: для отдельных балок в пределах ξ = 0,3 – 0,4, а для плит ξ =0,1 – 0,15. Обычно, исходя из конструктивных соображений, задаются высотой сечения hи его ширинойb, которые при необходимости уточняются методом последовательных приближений. Величины х и As находятся с помощью описанных выше соотношений или с помощью табличного метода.
Табличный метод подбора сечений был разработан для упрощения расчетов, и состоит в следующем. Преобразуем соотношения (3.4) и (3.5) к виду
где: A0 = ξ (1 – 0,5 ξ), (3.13)
η = 1 – 0,5 ξ. (3.14)
По этим соотношениям для A0 и η составлены таблицы в зависимости от величины относительной высоты сжатой зоны ξ. Подбор сечения с помощью таблиц выполняется следующим образом. Из конструктивных соображений задаются шириной сечения b и рекомендованной величиной ξ, затем по величине ξпо таблице находят величину A0, и далее из соотношения (3.12) вычисляют необходимую рабочую высоту сечения
находят полную высоту h = h0 + a и округляют ее до унифицированного размера. Сечение арматуры As определяется через величину η
Табличным методом можно также воспользоваться и для проверки прочности сечения, с известными высотой, шириной и армированием.
Рассмотрим расчет прямоугольного сечения с двойной арматурой(рис. 3.4).
или быть больше его. Соответственно, моменту M1 соответствует часть растянутой арматуры As1, а моменту M2 – арматура As2. Схема приложения сил и геометрия рассматриваемого сечения приведены на рис 3.4. Для определения момента M1 определяем по формуле (3.7) граничную относительную высоту сжатой зоны бетона ξR, по ней высоту сжатой зоны хи по формуле (3.4) момент M1. Зная момент M1 по соотношению (3.5) определим As1
Рис.3.4. Схема усилий в нормальном сечении изгибаемого элемента с двойной арматурой
Затем из (3.17) вычисляем момент M2 = M – M1, а по нему из суммы моментов относительно центра тяжести растянутой арматуры получим площадь сечения сжатой арматуры
Осталось определить площадь растянутой арматуры As
Дата добавления: 2015-02-10 ; просмотров: 1220 ; Нарушение авторских прав
Тема 4. РАСЧЕТ ПРОЧНОСТИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ



4.1. Виды изгибаемых элементов и их конструктивные особенности
Изгибаемые железобетонные элементы применяют в виде плит и балок, которые могут быть самостоятельными конструкциями или входить в состав сложных конструкций и сооружений (ребристые перекрытия, элементы каркасов сооружений и т. п.)
· Плитой называют конструкцию, имеющую малую толщину плит назначают возможно меньшей, так как расход бетона на эти конструкции составляет значительную долю его общего расхода на сооружение. Наименьшая толщина плиты должна удовлетворять требованиям прочности и жесткости. Толщину монолитных плит принимают кратной 10 мм, но не менее: для покрытий – 40 мм, для междуэтажных перекрытий гражданских и промышленных зданий – соответственно 50 и 60 мм. Минимальная толщина сборных плит – 25…35 мм. Армируют плиты сварными сетками. Сетки располагают в соответствии с эпюрой изгибающих моментов со стороны растянутых волокон (см. рис. 9.6). Стержни рабочей арматуры принимают диаметром 3…12 мм, располагая их на участке с максимальным моментом, шагом 100…200 мм, на остальных участках плиты шаг должен быть не более 400 мм. Распределительные стержни, образующие совместно с рабочими стержнями сетку, обеспечивают правильное положение их при бетонировании, воспринимают не учитываемые расчетом усилия от усадки бетона и изменения температуры, а при действии местных нагрузок распределяют их на большую площадь. Распределительные стержни имеют диаметр 3…8 мм, шаг 250…350 мм, площадь поперечного сечения не менее 10 % от сечения рабочей арматуры. Армирование плит вязаными сетками применяют редко: при сложной конфигурации в плане, большом числе отверстий и т. п.
Рис. 4.1. Формы поперечных сечений балок и схемы армирования:
1 — напрягаемая арматура
· Балкой называют конструкцию, у которой размеры поперечного сечения h и b значительно меньше ее пролета l.
Поперечные сечения железобетонных балок без предварительного натяжения арматуры обычно бывают прямоугольные, тавровые (с полкой внизу или вверху), трапециевидные (рис. 4.1, а. г) и др. Характерными сечениями предварительно напряженных балок являются тавровое, двутавровое (рис. 4.1, д) и др. Высота балок изменяется в широких пределах и в зависимости от нагрузок и назначения конструкции составляет 1 /8 … 1 /15 пролета. В предварительно напряженных балках она может быть уменьшена до 1 /25 пролета. В целях типизации элементов высоту сечения h назначают кратной 50 мм, если она не более 600 мм, и кратной 100 мм при большей высоте. Ширину балок назначают (0,3. 0,5)h.
Армирование балок выполняют продольными рабочими стержнями, поперечной арматурой и монтажными стержнями, соединенными между собой в сварные (реже вязаные) каркасы. Продольную рабочую арматуру в балках (как и в плитах) укладывают в растянутых зонах согласно эпюре изгибающих моментов.
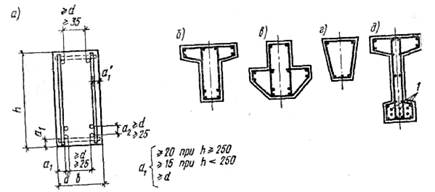
Размещают арматуру в один или два ряда по высоте сечения с такими зазорами, которые позволили бы провести плотную укладку бетона и обеспечили надежное сцепление арматуры с бетоном. Требуемые размеры этих зазоров и защитных слоев показаны на рис. 4.1, а. Для продольной ненапрягаемой арматуры обычно применяют стержни диаметром 12. 32 мм. Арматура диаметром более 32 мм вызывает трудности при производстве работ и используется реже.
Площадь сечения продольной рабочей арматуры должна быть не менее 0,05% от площади сечения бетона.
При недостаточной прочности бетона сжатой зоны, а также при действии в сечении моментов двух знаков рабочую арматуру устанавливают и в сжатой зоне (рис. 4.3, д). Монтажную арматуру принимают диаметром 10. 12 мм.
Прямоугольные и тавровые сечения шириной ребра 150 мм и менее можно армировать одним плоским сварным каркасом. При ширине балок более 150 мм устанавливают два или больше каркасов, которые объединяются в пространственные путем приварки поперечных соединительных стержней диаметром 5. 6 мм через 1. 1,5 м (см. рис. 1.4, б).
Поперечную арматуру ставят для воспринятия главных растягивающих напряжений, действующих в наклонных сечениях. Такой арматурой являются хомуты, иногда отгибы, устраиваемые обычно под углом 45°. Количество поперечной арматуры, ее диаметр и расстояние между стержнями определяют расчетом и конструктивными требованиями (см. § 4.3).
При высоте балок более 700 мм у боковых граней ставят дополнительные продольные стержни на расстояниях (по высоте) не более 400 мм. Эти стержни служат для воспринятия усилий от усадки бетона, температурных деформаций, а также они сдерживают раскрытие наклонных трещин на боковых гранях.
Предварительно напряженная арматура не входит в состав каркасов и размещается в соответствии с эпюрами моментов и поперечных сил. В однопролетных балках небольшой высоты предварительно напряженную арматуру обычно располагают в растянутой зоне прямолинейно по всей длине элемента (рис. 4.2, а). От внецентренно приложенной силы предварительного обжатия балка выгибается и в верхних волокнах появляются растягивающие напряжения по всей длине балки (рис. 4.2, б). При действии эксплуатационных нагрузок в верхней зоне возникают сжимающие напряжения (рис. 4.2, в). Суммируя эпюры напряжений (рис. 4.2, г), получают, что в верхних волокнах балки вблизи опор остаются растягивающие напряжения, которые могут вызвать образование трещин. Для погашения этих напряжений в балках иногда укладывают верхнюю арматуру A’sp в количестве 15. 25 % от нижней (рис. 4.2, д). В балках большой высоты часть напрягаемой арматуры располагают прямолинейно, а часть отгибают кверху (рис. 4.2, е). Это снижает растягивающие напряжения в верхних волокнах бетона вблизи опор и улучшает работу балки на главные растягивающие напряжения.
Для предварительно напряженных изгибаемых элементов характерны сечения с развитыми растянутой и сжатой зонами (двутавровые, тавровые). Сжатая полка развивается из условия прочности элементов под нагрузкой, обеспечения устойчивости верхнего пояса и опирания настила, растянутая — из условий размещения арматуры и обеспечения прочности сечения при обжатии. В предварительно напряженных элементах (рис. 4.2, ж. и) помимо напрягаемом арматуры укладывают и ненапрягаемую (расчетную и конструктивную), располагая ее ближе к поверхности элемента так, чтобы поперечная арматура охватывала всю продольную арматуру.
Особое значение в предварительно напряженных балках имеет конструирование концов элементов. Здесь происходит передача значительных усилий обжатия с арматуры на бетон, в результате чего возникают местные напряжения (см. гл. 3).Для обеспечения надежной анкеровки напрягаемой арматуры и с целью ограничения развития возможных (радиальных) трещин вдоль этой арматуры производят усиление концов элемента путем установки сварных сеток со стержнями d ≥ 4 мм, охватывающих все продольные стержни, дополнительных хомутов d ≥ 5 мм с шагом 50. 100 мм, располагаемых на участке не менее 0,6 1p, где 1p — определяется по формуле (3.1) (см. рис. 3.3, д).
Рис. 4.2. Схемы армирования балок предварительно
напряженной арматурой (а. е), размещение напрягаемой
арматуры в растянутой зоне балок (ж. и):
1 — напрягаемая арматура; 2 — хомуты;
3 — ненапрягаемая продольная арматура
В последние годы при проектировании изгибаемых элементов находит все более широкое применение смешанное армирование, представляющее сочетание ненапрягаемой и напрягаемой рабочей арматуры при разной величине предварительного напряжения. При использовании этого типа армирования представляется возможным расположить продольную рабочую арматуру в соответствии с эпюрой моментов и, оборвав часть или всю ненапрягаемую арматуру (оставив преднапряженную), получить экономию металла.
В изгибаемых элементах может быть также использована несущая (жесткая) арматура. При расположении этой арматуры ниже нейтральной оси сечения для обеспечения совместной работы с бетоном устраивают поперечные связи в виде хомутов или специальных анкерных стержней. Если нейтральная ось пересекает стенку высокого профиля жесткой арматуры, то совместная работа ее с бетоном обеспечивается без дополнительных поперечных стержней. Для уменьшения раскрытия трещин в обоих случаях устанавливают продольные стержни диаметром 8. 10 мм.
4.2. Расчет прочности по нормальным сечениям
Элементы прямоугольного сечения с одиночной арматурой. Расчет изгибаемых элементов по нормальным сечениям производится по стадии III напряженно-деформированного состояния. Для получения расчетных зависимостей проведем в балке (рис. 4.3, а) сечение, отбросим правую часть и заменим ее действие внутренними силами. Так как действительные законы распределения напряжений по сечению достаточно сложны, то принимают упрощающие предпосылки: 1) напряжения в бетоне в предельном состоянии принимают равными расчетному сопротивлению Rb; 2) действительная криволинейная эпюра напряжений в бетоне сжатой зоны заменяется прямоугольной; применение такой эпюры в качестве расчетной приводит к погрешностям, не превышающим 2. 8%, но позволяет упростить расчетные зависимости; 3) усилиями, воспринимаемыми растянутым бетоном над устьем трещины, пренебрегают вследствие их малости.
Прочность сечения элемента будет обеспечена, если расчетный момент от внешней нагрузки не превысит расчетного момента внутренних усилий относительно центра тяжести сечения растянутой арматуры (рис. 4.3 б):
или относительно центра тяжести сжатой зоны бетона
Рис. 4.3. К расчету сечений с одиночной (а, б, в, г) и двойной (д) арматурой;
к определению граничной высоты сжатой зоны (в)
Входящие в формулы (4.2), (4.3) напряжения в растянутой арматуре σs определяются характером разрушения, зависят от содержания арматуры в сечении, высоты сжатой зоны и т. п. и находятся по эмпирической формуле
где ω — параметр, характеризующий условную высоту прямоугольной эпюры сжатой зоны бетона, при которой фактическая нейтральная ось проходит через центр тяжести растянутой арматуры (рис. 4.3, г), ω = 0,85—0,008 Rb; ξ = x/ho — относительная высота сжатой зоны; σsc,u — предельные напряжения в арматуре сжатой зоны, принимаемые при γb2 ≥ 1 — 400 МПа, при γb2 ≥ 1 — 500 МПа; σsp — предварительное напряжение в арматуре с учетом всех потерь и γsp xR разрушение произойдет по сжатому бетону (случай 2). В расчетной практике для установления границы используют не х, а относительную высоту сжатой зоны ξ=х/h0, которая характеризует основные параметры конструкции (классы бетона, арматуры, площадь сечения арматуры, бетона) и особенности напряженно-деформированного состояния. Значению xR соответствует граничное значение относительной высоты сжатой зоны, определяемое по формуле (4.5), полученной на основе формулы (4.4):
где σsR — напряжение в арматуре: для арматуры классов A-I, А-II, A-III, Bp-I σsR=Rs; для предварительно напряженной арматуры классов A-IV и выше σsR=Rs+400-σsp-Δσsp, здесь Δσsp — коэффициент, зависящий от класса арматуры и способа натяжения [1].
Таким образом, при ξ≤ξR расчет элементов следует производить по случаю 1, при ξ>ξR — по случаю 2.
● Случай 1 (ξ≤ξR). С учетом вышеизложенного формулы (4.1). (4.3) примут такой вид:
Из формулы (4.8) высота сжатой зоны
Относительная высота сжатой зоны
где μ=As/(bh0)—коэффициент армирования. В расчетной практике часто используют также понятие «процент армирования» μ% = μ100%.
Пользуясь полученными формулами, можно решать задачи расчета сечений. Для упрощения практических расчетов формулы преобразуют, вводя параметры αm и ζ. Подставив в формулу (4.6) x = ξh0, получим
Аналогично, преобразуя уравнение (4.7), будем иметь
Полученные формулы справедливы при
Величины ξ, αm и ζ взаимно связаны друг с другом. Зная одну из них или задаваясь одной из них, можно с помощью табл. 4.1 найти любую другую.
Одинаковую несущую способность можно обеспечить при различных размерах сечения и соответственно разных процентах армирования. Так, с увеличением высоты сечения можно уменьшить количество арматуры и наоборот. При проектировании следует исходить из наиболее экономичных решений, для которых стоимость конструкций будет наименьшей. Исследования показывают, что экономичные решения будут получены при ξ=0,25. 0,4 для балок и ξ = 0,1. 0,2 для плит. Максимальное значение коэффициента армирования, при котором сечение будет работать по случаю 1, получим, подставляя граничное значение высоты сжатой зоны ξR в формулу (4.10), откуда μmax = ξRRb/Rs.
Для железобетонных изгибаемых элементов из бетона классов В12,5. В30, армированных сталями классов А-II, А-III, Вр-I, μmax=1,3. 3,2 %.
Нормы ограничивают и минимальный процент армирования, назначаемый из условия равнопрочности армированного и неармированного сечений. Для изгибаемых элементов μmin=0,05 %. Если процент армирования элемента ниже указанного минимума, то расчет следует производить без учета арматуры, т. е. как неармированного бетонного элемента.
В последнем случае прочность элемента из тяжелого бетона рассчитывается по формуле
Значения коэффициентов ξ, ζ, и αm для расчетов
изгибаемости элементов прямоугольного сечении
| ξ | ζ | αm | ξ | ζ | αm |
| 0,01 | 0,995 | 0,01 | 0,36 | 0,82 | 0,295 |
| 0,02 | 0,99 | 0,02 | 0,37 | 0,815 | 0,301 |
| 0,03 | 0,985 | 0,03 | 0,38 | 0,81 | 0,309 |
| 0,04 | 0,98 | 0,039 | 0,39 | 0,805 | 0,314 |
| 0,05 | 0,975 | 0,048 | 0,4 | 0,8 | 0,32 |
| 0,06 | 0,97 | 0,058 | 0,41 | 0,795 | 0,326 |
| 0,07 | 0,965 | 0,067 | 0,42 | 0,79 | 0,332 |
| 0,08 | 0,96 | 0,077 | 0,43 | 0,785 | 0,337 |
| 0,09 | 0,955 | 0,085 | 0,44 | 0,78 | 0,343 |
| 0,1 | 0,95 | 0,095 | 0,45 | 0,775 | 0,349 |
| 0,11 | 0,945 | 0,104 | 0,46 | 0,77 | 0,354 |
| 0,12 | 0,94 | 0,113 | 0,47 | 0,765 | 0,359 |
| 0,13 | 0,935 | 0,121 | 0,48 | 0,76 | 0,365 |
| 0,14 | 0,93 | 0,13 | 0,49 | 0,755 | 0,37 |
| 0,15 | 0,925 | 0,139 | 0,5 | 0,75 | 0,375 |
| 0,16 | 0,92 | 0,147 | 0,51 | 0,745 | 0,38 |
| 0,17 | 0,915 | 0,155 | 0,52 | 0,74 | 0,385 |
| 0,18 | 0,91 | 0,164 | 0,53 | 0,735 | 0,39 |
| 0,19 | 0,905 | 0,172 | 0,54 | 0,73 | 0,394 |
| 0,20 | 0,9 | 0,18 | 0,55 | 0,725 | 0,399 |
| 0,21 | 0,895 | 0,188 | 0,56 | 0,72 | 0,403 |
| 0,22 | 0,89 | 0,196 | 0,57 | 0,715 | 0,408 |
| 0,23 | 0,885 | 0,203 | 0,58 | 0,71 | 0,412 |
| 0,24 | 0,88 | 0,211 | 0,59 | 0,705 | 0,416 |
| 0,25 | 0,875 | 0,219 | 0,6 | 0,7 | 0,42 |
| 0,26 | 0,87 | 0,226 | 0,61 | 0,695 | 0,424 |
| 0,27 | 0,865 | 0,236 | 0,62 | 0,69 | 0,428 |
| 0,28 | 0,86 | 0,241 | 0,63 | 0,685 | 0,432 |
| 0,29 | 0,855 | 0,248 | 0,64 | 0,68 | 0,435 |
| 0,30 | 0,85 | 0,255 | 0,65 | 0,675 | 0,439 |
| 0,31 | 0,845 | 0,262 | 0,66 | 0,67 | 0,442 |
| 0,32 | 0,84 | 0,269 | 0,67 | 0,665 | 0,446 |
| 0,33 | 0,835 | 0,275 | 0,68 | 0,66 | 0,449 |
| 0,34 | 0,83 | 0,282 | 0,69 | 0,655 | 0,452 |
| 0,35 | 0,825 | 0,289 | 0,7 | 0,65 | 0,455 |
где Wpl — упругопластический момент сопротивления бетонного сечения; для элементов прямоугольного профиля Wpl = bh 2 /3,5[l].
При расчете сечений встречаются со следующими основными задачами: определение площади растянутой арматуры As; подбор размеров поперечного сечения элемента b и h и арматуры As; проверка несущей способности сечения. При проверке несущей способности определяют х из (4.9) и подставляют его значение в (4.6) или (4.7). При расчете As из (4.11) находят αm, затем по табл. 4.1 определяют ξ и по (4.14) вычисляют As. Блок-схемы решения указанных задач приведены в приложениях.
● Случай 2 (ξ>ξR). При расчете используют условия (4.1). (4.3). Расчет элементов из бетона классов В30 и ниже с ненапрягаемой арматурой классов A-I, A-II, А-III при x>ξRh0 допускается производить по формулам случая 1, подставляя в них x= ξRh0. В этом случае момент, воспринимаемый прямоугольным сечением с одиночной арматурой, будет
Элементы с избыточным содержанием арматуры — «переармированные» (ξ>ξR) — экономически невыгодны, так как прочностные свойства арматуры используются не полностью и это приводит к перерасходу стали. Поэтому изгибаемые элементы следует проектировать так, чтобы соблюдалось условие x ≤ ξRh0.
■ Элементы прямоугольного сечения с двойной арматурой. Сечениями с двойной арматурой называют такие, в которых кроме растянутой арматуры ставится по расчету сжатая. Необходимость в сжатой арматуре возникает, когда сечение с одиночной арматурой не может воспринять расчетный момент от внешней нагрузки вследствие недостаточной прочности бетона сжатой зоны (разрушение по случаю 2). Чтобы сжатая зона в таких конструкциях восприняла все сжимающие усилия, ее необходимо усилить арматурой. Сечения с двойной арматурой неэкономичны по расходу стали, так как увеличивается расход продольной арматуры и требуется постановка поперечных стержней (с шагом не более 15d в вязаных каркасах и 20d — в сварных), обеспечивающих закрепление сжатых рабочих продольных стержней от выпучивания. Поэтому сжатую арматуру ставят по расчету только в особых случаях: при ограниченных размерах поперечного сечения элемента; невозможности повышения класса бетона; при действии изгибающих моментов двух знаков или других специальных требованиях.
Формулы для расчета нормальных сечений элементов с двойной арматурой получены из тех же условий, что и для элементов с одиночной. В соответствии с расчетной схемой (рис. 4.3, д) условие прочности изгибаемого элемента в предельном состоянии имеет вид
а уравнение проекций всех сил на горизонтальную ось
где Мb — момент, воспринимаемый сжатой зоной бетона и соответствующей частью растянутой арматуры; M’s — момент, воспринимаемый сжатой арматурой A’s и соответствующей частью растянутой.
При расчете сечений элементов с двойной арматурой могут встретиться два типа задач: 1) сжатая арматура необходима для усиления сжатой зоны бетона (если увеличение размеров сечения нежелательно) и 2) сжатая арматура предусмотрена по конструктивным соображениям или при условии действия изгибающих моментов двух знаков. При решении задач первого типа в двух исходных уравнениях (4.18) и (4.19) оказывается три неизвестных х, As, A′s. Вследствие этого принимается дополнительное условие, которое отвечает экономическим требованиям.
Исследования показывают, что сечение будет наиболее экономичным, когда на бетон передается максимально возможное сжимающее усилие. Это будет иметь место при ξ = ξR. В этом случае сжатая арматура воспримет момент M’s=RscA’s(h0—a’) = M—αRRbbh 

Блок-схемы решения указанных задач приведены в приложениях.
Проверка несущей способности осуществляется по условию (4.18), при этом х находится из формулы (4.19).
Формулами (4.18). (4.19) можно пользоваться при х≥1,1а’. В противном случае сжатая арматура окажется вблизи нейтральной оси и напряжения в ней будут ниже Rsc.
■ Элементы таврового профиля. В первый период применения железобетона перекрытия сооружений выполнялись в виде сплошных плит. Однако такие конструкции нерациональны, поскольку сжатая зона составляет 1 /10… 1 /5 их высоты, а растянутая зона сечения бетона в расчете прочности не учитывается и служит для размещения арматуры (рис. 4.4, а). Если часть бетона из растянутой зоны удалить, оставив его только вблизи арматурных стержней, сведенных в группы, то получится ребристая плита (рис. 4.4, б). Несущая способность плиты при этом не изменится, а расход бетона и вес конструкции значительно уменьшатся. Такие элементы, называемые тавровыми, широко применяются в виде отдельных балок, настилов, в составе монолитных ребристых перекрытий и т. п.
Рис. 4.4. К расчету тавровых сечений
Опыты показывают, что полка (рис. 4.4, в) вовлекается в совместную работу с ребром сдвигающими усилиями, и на участках, удаленных от ребра, напряжения будут меньше. Это учитывается условным уменьшением вводимой в расчет ширины свесов. Например, для отдельных балок таврового сечения с консольными свесами вводимая в расчет ширина полки должна составлять [1]:
При расчете балок таврового сечения различают два случая: сжатая зона бетона находится в пределах полки (рис. 4.4, г) или ниже полки (рис. 4.4, д).
●Случай 1 (x>h’f) обычно встречается в сечениях с развитой полкой, когда внешний расчетный момент меньше внутреннего момента, воспринимаемого сжатой полкой сечения относительно центра тяжести арматуры:
Тавровые сечения этого типа рассчитывают как прямоугольные с размерами b′f и h, поскольку площадь растянутого бетона не влияет на несущую способность. Для расчета используют формулы (4.6). (4.9), полученные ранее для прямоугольного сечения с одиночной арматурой, в которых b заменяют на b’f. При относительно тонкой полке (h’f ≤ 0,2h) можно принять x=h’f и для определения площади арматуры пользоваться приближенной формулой
Коэффициент армирования для сечений, рассчитываемых по 1-му случаю, принимают μ=As/(bh0).
●Случай 2 (x>h’f) имеет место, если внешний расчетный момент будет больше внутреннего момента, воспринимаемого только сжатой полкой. Тавровые сечения этого типа встречаются при расчете балочных конструкций с малой шириной свесов полки.
Для получения расчетных зависимостей изгибающий момент, воспринимаемый сечением (рис. 4.4, д), разделяют на два заменяющих момента: Мfl (рис. 4.4, е), воспринимаемый свесами полок и соответствующей арматурой As,fl, и момент Мrib (рис. 4.4, ж), воспринимаемый сжатым бетоном ребра и соответствующей ему арматурой As,rib: M=Mfl+Mrib. Тогда из рис. 4.4, е
Определив Мfl по формуле (4.21), из формулы (4.22)
При известных М и Мfl площадь сечения арматуры подбирают как для обычного прямоугольного сечения шириной b на действие момента Mrib=M—Mfl: определяют αm=Mrib/(Rbbh 
Общая площадь продольной рабочей арматуры в тавровом сечении
Блок-схема расчета таврового сечения приведена в приложениях.
●Элементы, прямоугольного сечения, армированные напрягаемой и ненапрягаемой арматурой (смешанное армирование). Расчет прочности производят по III стадии напряженно-деформированного состояния, случаю 1 (ξ≤ξR). Предполагают, что напрягаемая арматура принята из высокопрочной стали, а ненапрягаемая — из мягких арматурных сталей с физическим пределом текучести. Рассматривая усилия, действующие в сечении (рис. 4.5, а), получают условие прочности. Для этого составляют уравнение моментов всех сил относительно центра тяжести растянутой арматуры
Положение нейтральной оси определяют из уравнения Σy=0:
Предполагают, что напряжения в бетоне и ненапрягаемой арматуре в предельном состоянии достигают расчетных значений Rb, Rs и Rsc. Напряжения в растянутой напрягаемой арматуре, не имеющей физического предела текучести, определяют произведением γs6Rs, где γs6 — коэффициент условий работы
здесь η — коэффициент, принимаемый равным для арматуры классов A-IV—1,2, A-V, B-II, К-7—1,15, A-VI—1,10.
Необходимость введения коэффициента γs6 обусловлена тем, что при достижении в арматуре напряжений σ0,2 (если ξ≤ξR) бетон сжатой зоны, как показывают опыты, не разрушается. При увеличении внешней нагрузки до значения, при котором разрушается бетон, удлинения растянутой арматуры возрастают, что приводит к росту в ней напряжений. Это явление не наблюдается в элементах, армированных сталями, имеющими физический предел текучести. Повышение напряжений зависит от характера диаграммы растяжения стали и величины ξ. С уменьшением ξ деформации растянутой арматуры к моменту разрушения сжатой зоны увеличиваются, напряжения в арматуре, не имеющей площадки текучести, повышаются.
Если в качестве ненапрягаемой арматуры As используют высокопрочную сталь, то в предельном состоянии напряжения в ней могут достичь расчетного сопротивления или быть ниже его значения в зависимости от величин ξ, σsp и соотношения классов напрягаемой и ненапрягаемой арматуры. Как показывают исследования, напряжения в ненапрягаемой арматуре, принятой одного класса с напрягаемой, достигают значения Rs при ξ≤0,5ξR и относительно невысокой степени предварительного напряжения арматуры Asp.
Напряжения в арматуре A’sp
Формула выражает тот факт, что до приложения внешней нагрузки в арматуре A’sp действует растягивающее предварительное напряжение σ’sp (c учетом потерь и коэффициента точности натяжения γsp>l). Внешняя нагрузка вызывает сжимающие напряжения, предельные значения которых при коэффициенте условий работы бетона γb2≥1 составляют 400 МПа, а при γb2 0), при γspσ′sp>400 (или 500) предварительное напряжение не будет погашено (σ′sp