связь между алгеброй логики и двоичным кодированием
Связь между алгеброй логики и двоичным кодированием
СВЯЗЬ МЕЖДУ АЛГЕБРОЙ ЛОГИКИ И ДВОИЧНЫМ КОДИРОВАНИЕМ Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0” Из этого следует два вывода: одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных; на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. Существуют различные физические способы кодирования двоичной информации, но чаще всего единица кодируется более высоким уровнем напряжения, чем ноль
Логический элемент компьютера
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ КОМПЬЮТЕРА Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями ), а также триггер С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”) Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем Работу логических элементов описывают с помощью таблиц истинности Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний
Логический элемент и
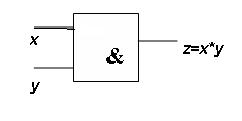
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ И Схема И реализует конъюнкцию двух или более логических значений Условное обозначение на структурных схемах схемы И с двумя входами Таблица истинности схемы И x y x ^ y 0 0 0 0 1 0 1 0 0 1 1 1 Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x ^ y (читается как » x и y » ) Операция конъюнкции на функциональных схемах обозначается знаком “&” (читается как «амперсанд»), являющимся сокращенной записью английского слова and
Логический элемент или
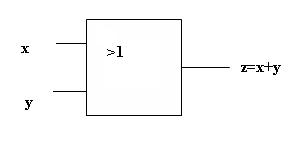
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ ИЛИ Схема ИЛИ реализует дизъюнкцию двух или более логических значений Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица Условное обозначение схемы ИЛИ Таблица истинности схемы ИЛИ x y x v y 0 0 0 0 1 1 1 0 1 1 1 1 Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как » x или y «)
Какая связь между алгеброй логики и двоичным кодированием?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
В каком виде записываются в памяти компьютера и в регистрах процессора данные и команды?
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. Мы уже рассмотрели способы записи двоичной информации на магнитных дисках и на CD-ROM. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
Что такое логический элемент компьютера?
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
| Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
Что такое схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ?
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.1.
Таблица истинности схемы И
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. 5.2. Знак «1» на схеме — от устаревшего обозначения дизъюнкции как «>=1» (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как «x или y»).
Таблица истинности схемы ИЛИ
С х е м а НЕ
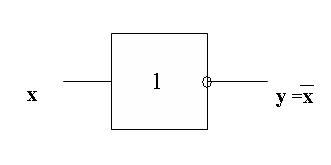
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z = 

Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора — на рисунке 5.3
Таблица истинности схемы НЕ
| x |  |
С х е м а И—НЕ
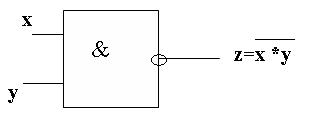
Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: 

Таблица истинности схемы И—НЕ
| x | y |  |
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом: 

Таблица истинности схемы ИЛИ—НЕ
| x | y |  |
Что такое триггер?
| Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. |
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.
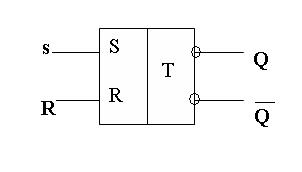
Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера — на рис. 5.6.

Рис. 5.6
Он имеет два симметричных входа S и R и два симметричных выхода Q и 

На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( 
Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.
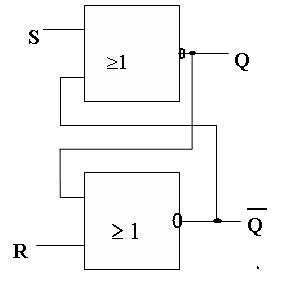
На рис. 5.7 показана реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.

Рис. 5.7
| S | R | Q |  |
| запрещено | |||
| хранение бита |
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ—НЕ (табл. 5.5).
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 2 10 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
Что такое сумматор?
| Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел. |
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
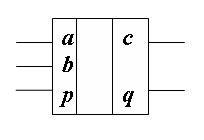
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора на рис. 5.8.

Рис. 5.8
При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:
1. цифра ai первого слагаемого;
2. цифра bi второго слагаемого;
3. перенос pi–1 из младшего разряда.
В результате сложения получаются две цифры:
1. цифра ci для суммы;
2. перенос pi из данного разряда в старший.
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:
| Входы | Выходы | |||
| Первое слагаемое | Второе слагаемое | Перенос | Сумма | Перенос |
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Например, схема вычисления суммы C = (с3 c2 c1 c0) двух двоичных трехразрядных чисел A = (a2 a1 a0) и B = (b2 b1 b0) может иметь вид:
5.3. Какая связь между алгеброй логики и двоичным кодированием? 5.5. Что такое логический элемент компьютера?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: «1» и «0».
Из этого следует два вывода:
- 1. одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
2. на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
5.4. В каком виде записываются в памяти компьютера и в регистрах процессора данные и команды?
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины.
Существуют различные физические способы кодирования двоичной информации, но чаще всего единица кодируется более высоким уровнем напряжения, чем ноль (или наоборот), например:
5.5. Что такое логический элемент компьютера?
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Конспект на тему «Связь между алгеброй логики и двоичным кодированием»
Новые аудиокурсы повышения квалификации для педагогов
Слушайте учебный материал в удобное для Вас время в любом месте
откроется в новом окне
Выдаем Удостоверение установленного образца:
Какая связь между алгеброй логики и двоичным кодированием?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Информатика: теория и методика преподавания в образовательной организации
Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-252784
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
ВПР начались в колледжах с 15 сентября
Время чтения: 4 минуты
Аккаунты друзей ребенка в соцсетях регулярно просматривают 30% родителей
Время чтения: 2 минуты
ЕГЭ в 2022 году может пройти в допандемийном формате
Время чтения: 1 минута
Всероссийская олимпиада школьников начнется 13 сентября
Время чтения: 2 минуты
В пяти регионах России протестируют новую систему оплаты труда педагогов
Время чтения: 2 минуты
Игры со взрослыми полезнее для развития детей, чем игры со сверстниками
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Какая связь между алгеброй логики и двоичным кодированием?



Математический аппарат алгебры логики удобен для обработки данных в компьютере, где применяется двоичная система счисления, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Поэтому одни и те же устройства компьютера могут применяться как для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и значений логических переменных.
Данные и команды также представляются в виде двоичных последовательностей 0 и 1 различной структуры и длины.
На физическом уровне кодирования двоичной информации единица кодируется более высоким уровнем напряжения, чем ноль (или наоборот).
Что такое логический элемент компьютера?
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение в схеме, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
| Таблица истинности это табличное представление логической схемы (или операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
Схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.1. Таблица истинности — в таблице 5.1.
Единица на выходе схемы “И” будет тогда и только тогда, когда на всех входах будут единицы.
Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x Ù y (читается как «x и y»).
Операция конъюнкции на функциональных схемах обозначается знаком “&” (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует операцию дизъюнкцию для двух или более логических значений.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение схемы ИЛИ представлено на рис. 5.2. Значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x Ú y (читается как «x или y«). Таблица истинности — в табл. 5.2.
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z = 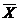
| X | 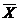 |
С х е м а И – НЕ
Схема И-НЕсостоит из элемента И и инвертора и осуществляет отрицание результата схемы И.
Связь между выходом z и входами x и y схемы записывают следующей формулой: z = 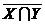
Условное обозначение схемы И-НЕ представлено на рисунке 5.4.
Таблица истинности схемы И-НЕ — в табл. 5.4.
| x | y | 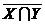 |
С х е м а ИЛИ – НЕ
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами x и y схемы записывают следующим образом: z = 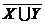
Таблица истинности схемы ИЛИ-НЕ — в табл. 5.5.
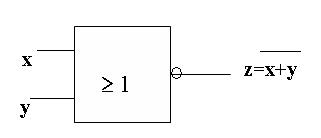
Рис. 5.5
| x | y | 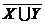 |
Что такое триггер?
| Триггер — это электронная схема, применяемая в регистрах компьютера для запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. |
Термин триггер в схемах имеет название f lip-flop, что в переводе означает “хлопанье”. Самый распространённый тип триггера — так называемый RS-триггер ( S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера в схемах — на рис. 5.6.
Он имеет два симметричных входа S и R и два симметричных выхода Q и ┐Q, причем выходной сигнал ┐Q является логическим отрицанием сигнала Q.
Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.
На рис. 5.7 показана реализация триггера с помощью двух вентилей ИЛИ-НЕ и соответствующая таблица истинности.
| S | R | Q | ØQ |
| запрещено | |||
| обнуление бита |
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ (табл. 5.5).
1. Если на входы триггера подать S=“1”, R=“0”, то (независимо от начального состояния) на выходе Q верхнего вентиля появится “0”. После этого на входах нижнего вентиля окажется R= “0”, Q =“0” и выход 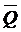
2. Точно так же при подаче “0” на вход S и “1” на вход R на выходе 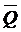
3. Если на входы R и S подана логическая “1”, то состояние Q и 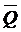
Подача на оба входа R и S логического “0” может привести к неоднозначному результату, поэтому такая комбинация для входных сигналов запрещена.
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 • 2 10 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
Что такое сумматор?
| Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел. |
Многоразрядный двоичный сумматор предназначен для сложения многоразрядных двоичных чисел и представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение (в схемах) одноразрядного сумматора на рис. 5.8.
При сложении двух чисел a и b в одном i-ом разряде приходится иметь дело с тремя цифрами:
1. цифра ai первого слагаемого;
2. цифра bi второго слагаемого;
3. перенос цифры pi–1 из младшего разряда в старший разряд.
В результате сложения получаются две цифры c и q :
1. цифра ci для суммы данного i-го разряда;
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:
| Входы | Выходы | |||
| Первое слагаемое | Второе слагаемое | Перенос pi-1 | Сумма ci | Перенос pi |
Если требуется складывать двоичные числа длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.