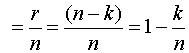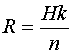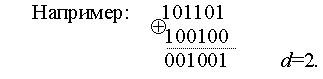сжимающее и помехоустойчивое кодирование информации

Шифрование, помехоустойчивое кодирование и сжатие информации

Цель лекции: познакомиться с принципами совместного использования шифрования, помехоустойчивого кодирования и сжатия информации для комплексной защиты информации в процессе ее передачи и хранения.

Проблемы передачи информации и их комплексное решение

В процессе передачи информации от источника к потребителю на информацию воздействуют различные неблагоприятные факторы. Криптографические методы защищают информацию только от одного вида разрушающих воздействий – от предумышленного разрушения или искажения информации. Однако на практике при передаче информации от абонента к абоненту возможны случайные помехи на линиях связи, ошибки и сбои аппаратуры, частичное разрушение носителей данных и т.д. Таким образом, в реальных системах связи существует проблема защиты информации от случайных воздействий.

В связи с появлением сетей передачи данных высокой пропускной способности и развитием мультимедиа-технологий возникает проблема шифрования больших объемов информации. Если раньше основным типом шифруемых и передаваемых сообщений было текстовое сообщение, то в ХХI веке криптографическая защита все чаще применяется при передаче цифровых видео- и речевых сообщений, карт местности, для организации видеоконференций. Именно поэтому в последнее время возникает проблема шифрования огромных информационных массивов. Для интерактивных систем типа телеконференций, организации аудио- или видеосвязи, такое шифрование должно осуществляться в реальном режиме времени и по возможности быть незаметным для пользователей.

Решение указанных проблем, в том числе и защита от несанкционированного доступа, может быть достигнуто при комплексном использовании достижений теории информации.

Так, целью криптографического преобразования является, как известно, защита от несанкционированного доступа, аутентификация и защита от преднамеренных изменений. Помехоустойчивое кодирование выполняется с целью защиты информации от случайных помех при передаче и хранении. Эффективное кодирование производится с целью минимизации объема передаваемых или хранимых данных.

На практике эти три вида преобразования информации обычно используются совместно. Так, например, некоторые программные пакеты перед шифрованием архивируют обрабатываемые данные. С другой стороны, реальные системы передачи информации, будь то локальные и глобальные сети передачи данных, или компьютерные носители информации (CD или DVD-диски) всегда имеют в составе системы защиты информации средства контроля и коррекции случайных ошибок.

Для того, чтобы более эффективно использовать на практике криптографические методы защиты информации, рассмотрим основные положения теорий помехоустойчивого и эффективного кодирования, используемые в системах защиты информации.

Помехоустойчивое кодирование

Как уже отмечалось, вопросы криптографического преобразования информации тесно связаны с вопросами помехоустойчивого кодирования сообщений. Это обусловлено, с одной стороны (теоретической), тем, что и при криптографическом шифровании, и при помехоустойчивом кодировании используются одни и те же законы теории информации. С другой стороны (практической) процессы накопления, хранения и передачи информации протекают в условиях воздействия помех, способных исказить хранимые и обрабатываемые данные. Это обуславливает актуальность разработки и использования методов, позволяющих обнаруживать и корректировать подобные ошибки. С математической точки зрения задача сводится к синтезу так называемых помехоустойчивых кодов.

Аналогично понятию шифра в криптографии при обсуждении помехоустойчивого кодирования и вопросов сжатия сообщений вводят понятие кода. Вообще кодом называется совокупность знаков, а также система правил, позволяющая представлять информацию в виде набора таких знаков. Кодовым словом называют любой ряд допустимых знаков. Например, двоичное число 1100 можно считать двоичным 4-разрядным кодовым словом.

Общая идея помехоустойчивого кодирования состоит в том, что из всех возможных кодовых слов считаются допустимыми не все, а лишь некоторые из них. Например, в коде с контролем по четности считаются допустимыми лишь слова с четным числом единиц. Ошибка превращает допустимое слово в недопустимое и поэтому обнаруживается.

Помехоустойчивые коды делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Блоковые коды характеризуются так называемым минимальным кодовым расстоянием. Вообще, расстоянием по Хэммингу (по имени американского математика Р.У. Хэмминга) между двумя кодовыми словами называется число разрядов, в которых они различны. При этом в качестве минимального кодового расстояния выбирается наименьшее из всех расстояний по Хэммингу для любых пар различных кодовых слов, образующих код.

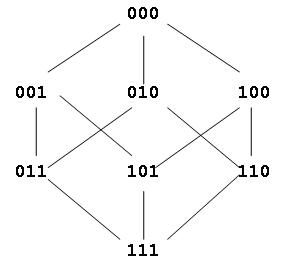
Например, пусть мы используем только трехразрядные двоичные слова. Всего таких кодовых слов может быть восемь. Те кодовые слова, которые отличаются только на одну единицу, называются соседними. Например, кодовые слова 101 и 111 – соседние, так как отличаются только средним разрядом, а слова 101 и 110 – не соседние, так как у них отличаются два последних разряда. Изобразим все трехразрядные двоичные комбинации и соединим линией соседние кодовые слова. Тогда мы получим схему, как на рис. 14.1. Минимальное кодовое расстояние между словами обычного, не помехоустойчивого кода равно единице.

В случае использования всех трехразрядных двоичных слов для передачи сообщений все они будут считаться допустимыми. Применим контроль по условию четности. Тогда допустимыми будут только выделенные рамками слова с четным числом единиц (см. рис. 14.2).

Источник

Электронные средства сбора, обработки и отображения информации

Оглавление

Помехоустойчивое кодирование

Понятие корректирующего кода

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.

Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).

В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.

Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой букве сообщения соответствует блок из п символов.

Блоковый код называется равномерным, если п (значность) остается одинаковой для всех букв сообщения.

Различают разделимые и неразделимые блоковые коды.

При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся частей: информационной и проверочной. Информационные и проверочные разряды во всех кодовых комбинациях разделимого кода занимают одни и те же позиции.

При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.

Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Общие принципы использования избыточности

Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На ввод кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n>k. Всего может быть различных входных последовательностей и различных выходных последовательностей. Из общего числа выходных последовательностей только последовательностей соответствуют входным. Будем называть их разрешенными кодовыми комбинациями. Остальные ( — ) возможных выходных последовательностей для передачи не используются. Их будем называть запрещенными кодовыми комбинациями.

— случаев безошибочной передачи;

— ·(-1) случаев перевода в другие разрешенные комбинации, что соответствует необнаруживаемым ошибкам;

— ·( — ) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены.

Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:

К_обн .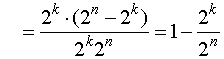

Рассмотрим, например, обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (п=k+1). Общее число выходных последовательностей составит , то есть вдвое больше общего числа кодируемых входных последовательностей. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество комбинаций, содержащих четное число единиц (или нулей). При кодировании к каждой последовательности из k информационных символов добавляется один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным. Искажение любого четного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть обнаруженных ошибок составляет:

К_обн .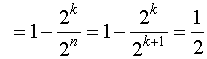

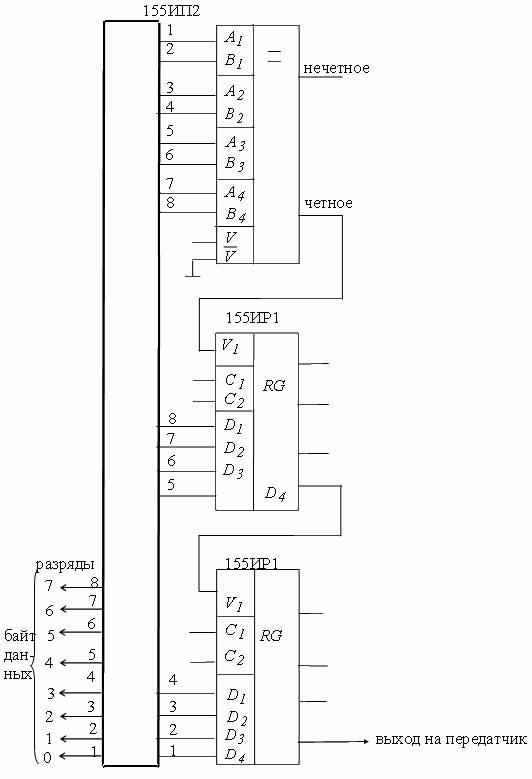
Пример кодирующего устройства с проверкой на четность показан на рис.

Основные параметры корректирующих кодов

Основными параметрами, характеризующими корректирующие свойства кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых или исправленных ошибок.

Рассмотрим суть этих параметров.

Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов

Относительной избыточностью корректирующего кода называют величину

_отн

_отн.

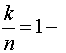
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. Ее еще называют относительной скоростью передачи информации.

Если производительность источника равна Н символов в секунду, то скорость передачи после кодирования этой информации будет равна

поскольку в последовательности из п символов только k информационных.

Если число ошибок, которое нужно обнаружить или исправить, значительно, необходимо иметь код с большим числом проверочных символов. Скорость передачи информации при этом будет уменьшена, так как появляется временная задержка информации. Она тем больше, чем сложнее кодирование.

Кодовое расстояние характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом символов, которыми комбинации отличаются одна от другой.

Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2.

Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до п, равной значности кода.

Число обнаруживаемых ошибок определяется минимальным расстоянием между кодовыми комбинациями. Это расстояние называется хэмминговым.

В безызбыточном коде все комбинации являются разрешенными, =1. Достаточно только исказиться одному символу, и будет ошибка в сообщении.

Теорема. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух.

Доказательство. Возьмем значность кода п=3. Возможные комбинации натурального кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как =1. Если =2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию.

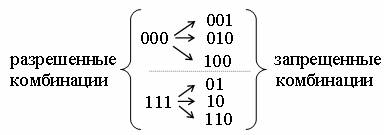
Пусть подмножество разрешенных комбинаций образовано по принципу четности числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:

Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к переходу комбинации в подмножество запрещенных комбинаций. То есть этот код обнаруживает все одиночные ошибки.

В общем случае при необходимости обнаруживать ошибки кратности — минимальное хэммингово расстояние должно быть, по крайней мере, на единицу больше , то есть

+1.

В этом случае никакая ошибка кратности не в состоянии перевести одну разрешенную комбинацию в другую.

Ошибки можно не только обнаруживать, но и исправлять.

Теорема. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех.

Доказательство. Пусть, как и в предыдущем примере, п=3. Примем разрешенные комбинации 000 и 111 (кодовое расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации образуются в результате возникновения единичной ошибки в комбинации 000.

Аналогично разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества запрещенных комбинаций, то очевидно, что они не пересекаются:

В общем случае исправляемые ошибки кратности связаны с кодовым расстоянием соотношением

=2+1. (2.1)

где — сочетание из п элементов по t (число возможных ошибок кратности t на длине п-разрядной комбинации).

Если, например, п=7, =1, то из (2.1)

Нужно отметить, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала связи.

Групповой код с проверкой на четность

Недостатком кода с четным числом единиц является необнаружение четных групповых ошибок. Этого недостатка лишены коды с проверкой на четность, где комбинации разбиваются на части, из них формируется матрица, состоящая из некоторого числа строк и столбцов:

Строки образуются последовательно по мере поступления символов исходного кода. Затем после формирования т строк матрицы производится проверка на четность ее столбцов и образуются контрольные символы . Контрольные символы образуются путем суммирования по модулю 2 информационных символов, расположенных в столбце:

.

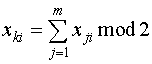
При таком кодировании четные групповые ошибки обнаруживаются. Не обнаруживаются лишь такие ошибки, при которых искажено четное число символов в столбце.

Можно повысить обнаруживающую способность кода путем одновременной проверки на четность по столбцам и строкам или столбцам и диагоналям (поперечная и диагональная проверка).

Если проверка проводится по строкам и столбцам, то код называется матричным.

Проверочные символы располагаются следующим образом:

;

.

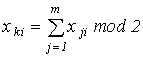
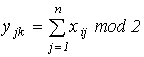
В этом случае не обнаруживаются только ошибки четной кратности с кратностью 4, 8, 16 и т.д., при которых происходит искажение символов с попарно одинаковыми индексами строк столбцов. Наименьшая избыточность кода получается в том случае, когда образуемая матрица является квадратной.

Недостатком такого кода является необходимость внесения задержки в передачу информации на время, необходимое для формирования матрицы.

Матричный код позволяет исправлять одиночные ошибки. Ошибочный элемент находится на пересечении строки и столбца, в которых имеется нарушение четности.

Коды с постоянным весом

Весом называется число единиц, содержащихся в кодовых комбинациях.

В коде «3 из 7» возможных комбинаций сто двадцать восемь (=128), а разрешенных кода только тридцать пять. Относительная избыточность _отн = 0,28.

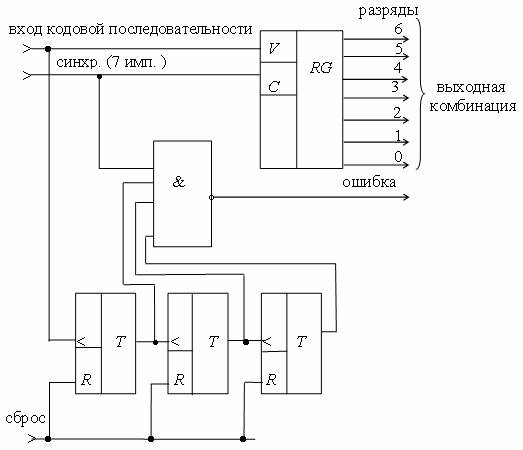
Схема устройства определения веса комбинаций кода «3 из 7» приведена на рис. 2.6.

Циклические коды

Циклические коды характеризуются тем, что при циклической перестановке всех символов кодовой комбинации данного кода образуется другая кодовая комбинация этого же кода.

— комбинация циклического кода;

— также комбинация циклического кода.

Например, комбинация 1001111 (п=7) будет представлена многочленом

При таком представлении действия над кодовыми комбинациями сводятся к действиям над многочленами. Эти действия производятся в соответствии с обычной алгебры, за исключением того, что приведение подобных членов осуществляется по модулю 2.

Обнаружение ошибок при помощи циклического кода обеспечивается тем, что в качестве разрешенных комбинаций выбираются такие, которые делятся без остатка на некоторый заранее выбранный полином G(x). Если принятая комбинация содержит искаженные символы, то деление на полином G(x) осуществляется с остатком. При этом формируется сигнал, свидетельствующий об ошибке. Полином G(x) называется образующим.

Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю 2:

Таким образом, все полиномы, отображающие комбинации циклического кода, будут иметь степень ниже п.

Часто в качестве полинома, на который осуществляется деление, берется полином G(x)=+1. При таком формировании кодовых комбинаций позиции информационных и контрольных символов заранее определить нельзя.

Большим преимуществом циклических кодов является простота построения кодирующих и декодирующих устройств, которые по своей структуре представляют регистры сдвига с обратными связями.

Число разрядов регистра выбирается равным степени образующего полинома.

Обратная связь осуществляется с выхода регистра на некоторые разряды через сумматоры, число которых выбирается на единицу меньше количества ненулевых членов образующего полинома. Сумматоры устанавливаются на входах тех разрядов регистра, которым соответствуют ненулевые члены образующего полинома.

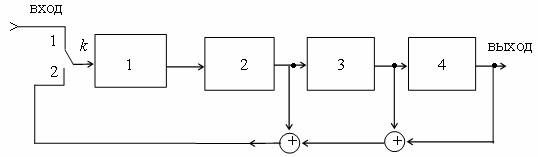
На рис. 2.7 приведена схема кодирующего регистра для преобразования четырехразрядной комбинации в семиразрядную.

В табл. 2.3 показано, как путем сдвигов исходной комбинации 0101 получается комбинация циклического кода 1010011. п=7, k=4. Комбинация 0101, ключ в положении 1. В течение первых четырех тактов регистр будет заполнен, затем ключ переводится в положение 2. Обратная связь замыкается. Под действием семи сдвигающих тактов проходит формирование семиразрядного циклического кода.

Свойства циклического кода:

1) циклический код обнаруживает все одиночные ошибки, если образующий полином содержит более одного члена. Если G(x)=x+1, то код обнаруживает одиночные ошибки и все нечетные;

2) циклический код с G(x)=(x+1)G(x) обнаруживает все одиночные, двойные и тройные ошибки;

Источник