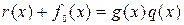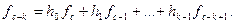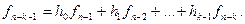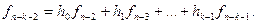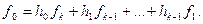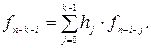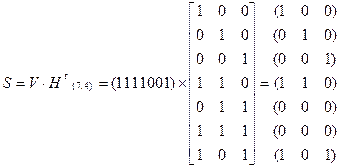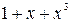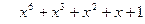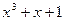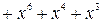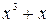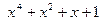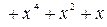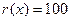технические средства кодирования и декодирования циклических кодов
6.12.6. Технические средства кодирования и декодирования для циклических кодов
6.12.6.1. Линейные переключательные схемы
Основу кодирующих и декодирующих устройств циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю два. Такие регистры также называют многотактными линейными переключательными схемами и линейными кодовыми фильтрами Хаффмена. Они состоят из ячеек памяти, сумматоров по модулю два и устройств умножения на коэффициенты многочленов множителя или делителя. В случае двоичных кодов для умножения на коэффициент, равный 1,требуется только наличие связи в схеме. Если коэффициент равен 0,то связь отсутствует. Сдвиг информации в регистре осуществляется импульсами, поступающими с генератора продвигающих импульсов, который на схеме, как правило, не указывается. На вход устройств поступают только коэффициенты многочленов, причем начиная с коэффициента при переменной в старшей степени.
Р ис 6.11.Схема произведения многочленов
П роизведение этих многочленов равно
Предполагаем, что первоначально ячейки памяти находятся в нулевом состоянии и что за коэффициентами множимого следует n—kнулей.
На первом такте на вход схемы поступает первый коэффициент ak-1многочленаa(x) и на выходе появляется первый коэффициент произведения, равныйak-1g n—k. На следующем такте на выход поступит суммаa k-2g n—k+a k-1gn—k-1, т.е. второй коэффициент произведения, и т.д. На n-м такте все ячейки, кроме последней, будут в нулевом состоянии и на выходе получим последний коэффициент a0g0.
Используется также схема умножения многочленов при поступлении множимого младшим разрядом вперед (рис. 6.12).
Рис 6.12. Схема умножения
Рис 6.13. Схема деления
За первые n—kтактов коэффициенты многочлена-делимого заполняют регистр, причем коэффициент при в старшей степени достигает крайней правой ячейки. На следующем такте «единица» делимого, выходящая из крайней ячейки регистра, по цепи обратной связи подается к сумматорам по модулю два, что равносильно вычитанию многочлена-делителя из многочлена-делимого. Если в результате предыдущей операции коэффициент при старшей степени х у остатка оказался равным нулю, то на следующем такте делитель не вычитается. Коэффициенты делимого только сдвигаются вперед по регистру на один разряд, что находится в полном соответствии с тем, как это делается при делении многочленов столбиком.
Деление заканчивается с приходом последнего символа многочлена-делимого. При этом разность будет иметь более низкую степень, чем делитель. Эта разность и есть остаток.
Отметим, что если в качестве многочлена-делителя выбран простой многочлен степени m = n—k,то, продолжая делить образовавшийся остаток при отключенном входе, будем получать в регистре по одному разу каждое из ненулевыхm-разрядных двоичных чисел. Затем эта последовательность чисел повторяется.
§ 6.8 Технические средства кодирования и декодирования для циклических кодов
Линейные переключательные схемы.Основу кодирующих и декодирующих устройств циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю два. Такие регистры также называют многотактными линейными переключательными схемами и линейными кодовыми фильтрами Хаффмена. Они состоят из ячеек памяти, сумматоров по модулю два и устройств умножения на коэффициенты многочленов множителя или делителя. В случае двоичных кодов для умножения на коэффициент, равный 1, требуется только наличие связи в схеме. Если коэффициент равен 0, то связь отсутствует. Сдвиг информации в регистре осуществляется импульсами, поступающими с генератора продвигающих импульсов, который на схеме, как правило, не указывается. На вход устройств поступают только коэффициенты многочленов, причем начиная с коэффициента при переменной в старшей степени.
Предполагаем, что первоначально ячейки памяти находятся в нулевом состоянии и что за коэффициентами множимого следует n — k нулей.
На первом такте на вход схемы поступает первый коэффициент ak-1 многочлена а(х) и на выходе появляется первый коэффициент произведения, равный аk-1,gn—k. На следующем такте на выход поступит сумма ak-2 gn—k+ak-1gn—k-1, т.е. второй коэффициент произведения, и т. д. На n-м такте все ячейки, кроме последней, будут в нулевом состоянии и на выходе получим последний коэффициент a0g0.
Используется также схема умножения многочленов при поступлении множимого младшим разрядом вперед (рис. 6.11).
За первые n — k тактов коэффициенты многочлена-делимого заполняют регистр, причем коэффициент при x в старшей степени достигает крайней правой ячейки. На следующем такте «единица» делимого, выходящая из крайней ячейки регистра, по цепи обратной связи подается к сумматорам по модулю два, что равносильно вычитанию многочлена-делителя из многочлена-делимого. Если в результате предыдущей операции коэффициент при старшей степени x у остатка оказался равным нулю, то на следующем такте делитель не вычитается. Коэффициенты делимого только сдвигаются вперед по регистру на один разряд, что находится в полном соответствии с тем, как это делается при делении многочленов столбиком.
Деление заканчивается с приходом последнего символа многочлена-делимого. При этом разность будет иметь более низкую степень, чем делитель. Эта разность и есть остаток.
Отметим, что если в качестве многочлена-делителя выбран простой многочлен степени m = n — k, то, продолжая делить образовавшийся остаток при отключенном входе, будем получать в регистре по одному разу каждое из ненулевых m-разрядных двоичных чисел. Затем эта последовательность чисел повторяется.
П
Вычисление остатка начинается с четвертого такта и заканчивается после седьмого такта. Последующие сдвиги приводят к образованию в регистре последовательности из семи различных ненулевых трехразрядных чисел. В дальнейшем эта последовательность чисел повторяется.
Рассмотренные выше схемы умножения и деления многочленов непосредственно в том виде, в каком они представлены на рис. 6.11, 6.12, в качестве кодирующих устройств циклических кодов на практике не применяются: первая — из-за того, что образующаяся кодовая комбинация в явном виде не содержит информационных символов, а вторая — из-за того, что между информационными и проверочными символами образуется разрыв в n — k разрядов.
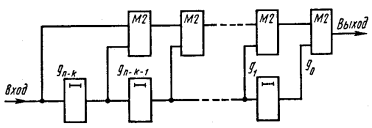
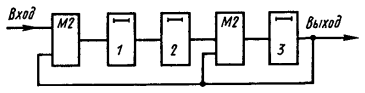
Кодирующие устройства. Все известные кодирующие устройства для любых типов циклических кодов, выполненные на регистрах сдвига, можно свести к двум типам схем согласно рассмотренным ранее методам кодирования.
С
В исходном состоянии ключ К1 находится в положении 1. Информационные символы одновременно поступают как в линию связи, так и в регистр сдвига, где за k тактов образуется остаток. Затем ключ Κ1 переходит в положение 2 и остаток поступает в линию связи.
Пример 6.16. Рассмотрим процесс деления многочлена а(х)х m = = (х 3 + +1)x 3 на многочлен g(x) = x 3 + x 2 + 1 за k тактов
Схема кодирующего устройства для заданного g(x) приведена на рис 6.15 
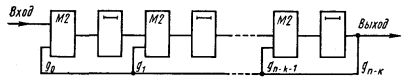
С
В исходном положении ключ Κ1 находится в положении 1. За первые k тактов поступающие на вход информационные символы заполняют все ячейки регистра. После этого ключ переводят в положение 2. На каждом из последующих тактов один из информационных символов выдается в канал связи и одновременно формируется проверочный символ, который записывается в последнюю ячейку регистра. Через n — k тактов процесс формирования проверочных символов заканчивается и ключ Κ1 снова переводится в положение 1.
В течение последующих k тактов содержимое регистра выдается в канал связи с одновременным заполнением ячеек новой последовательности информационных символов.
Пример 6.17. Рассмотрим процесс формирования кодовой комбинации с использованием генераторного многочлена для случая g(x) = = х 3 + х 2 + 1 и а(х) = =х 3 +1
Определяем генераторный многочлен.
С
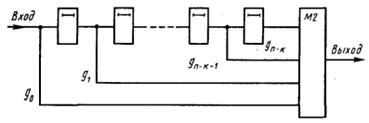
Декодирующие устройства.Декодирование комбинаций циклического кода можно проводить различными методами. Существуют методы, основанные на использовании рекуррентных соотношений, на мажоритарном принципе, на вычислении остатка от деления принятой комбинации на образующий многочлен кода и др. Целесообразность применения каждого из них зависит от конкретных характеристик используемого кода.
Рассмотрим сначала устройства декодирования, в которых для обнаружения и исправления ошибок производится деление произвольного многочлена f(x), соответствующего принятой комбинации, на образующий многочлен кода go(x). В этом случае при декодировании могут использоваться те же регистры сдвига, что и при кодировании.
Декодирующие устройства для кодов, обнаруживающих ошибки, по существу ничем не отличаются от схем кодирующих устройств. В них добавляется лишь буферный регистр для хранения принятого сообщения на время проведения операции деления. Если остатка не обнаружено (случай отсутствия ошибки), то
информация с буферного регистра считывается в дешифратор сообщения. Если остаток обнаружен (случай наличия ошибки), то информация в буферном регистре уничтожается и на передающую сторону посылается импульс запроса повторной передачи.
В
Символы подлежащей декодированию кодовой комбинации, возможно, содержащей ошибку, последовательно, начиная со старшего разряда, вводятся в n-разрядный буферный регистр сдвига и одновременно в схему деления, где за n тактов определяется остаток, который в случае непрерывной передачи сразу же переписывается в регистр второй аналогичной схемы деления.
Начиная с (n + 1)-го такта в буферный регистр и первую схему деления начинают поступать символы следующей кодовой комбинации. Одновременно на каждом такте буферный регистр покидает один символ, а в регистре второй схемы деления появляется новый остаток (синдром). Детектор ошибок, контролирующий состояния ячеек этого регистра, представляет собой комбинаторно-логическую схему, построенную с таким расчетом, чтобы она отмечала все те синдромы («выделенные синдромы»), которые появляются в схеме деления, когда каждый из ошибочных символов занимает крайнюю правую ячейку в буферном регистре. При последующем сдвиге детектор формирует сигнал «1», который, воздействуя на сумматор коррекции, исправляет искаженный символ.
Одновременно по цепи обратной связи с выхода детектора подается сигнал «1» на входной сумматор регистра второй схемы деления. Этот сигнал изменяет выделенный синдром так, чтобы он снова соответствовал более простому типу ошибки, которую еще подлежит исправить. Продолжая сдвиги, обнаружим и другие выделенные синдромы. После исправления последней ошибки все ячейки декодирующего регистра должны оказаться в нулевом состоянии. Если в результате автономных сдвигов состояние регистра не окажется нулевым, это означает, что произошла неисправимая ошибка.
Для декодирования кодовых комбинаций, разнесенных во времени, достаточно одной схемы деления, осуществляющей декодирование за 2n тактов.
Сложность детектора ошибок зависит от числа выделенных синдромом. Простейшие детекторы получаются при реализации кодов, рассчитанных на исправление единичных ошибок.
Выделенный синдром появляется в схеме деления раньше всего в случае, когда ошибка имеет место в старшем разряде кодовой комбинации, так как он первым достигает крайней правой ячейки буферного регистра. Поскольку неискаженная кодовая комбинация делится на g0(x) без остатка, то для определения выделенного синдрома достаточно разделить на g0(x) вектор ошибки с единицей в старшем разряде. Остаток, получающийся на n-м такте, и является искомым выделенным синдромом.
В зависимости от номера искаженного разряда после первых тактов будем получать различные остатки (опознаватели соответствующих векторов ошибок). Вследствие этого выделенный синдром будет появляться в регистре схемы деления через различное число последующих тактов, обеспечивая исправление искаженного символа.
Пример 6.18. Рассмотрим процесс исправления единичной ошибки при использовании кода (7,4) с образующим многочленом g(x) = х 3 + x 2 + 1 и применении в декодирующем устройстве схем деления за n и k тактов.
Определим опознаватели ошибок и выделенный синдром для случая использования схемы деления за n тактов:
Технические средства кодирования и декодирования для групповых кодов
4.8.5 Технические средства кодирования и декодирования для групповых кодов
Кодирующее устройство строится на основании совокупности равенств, отражающих правила построения кода. Определение значений символов в каждом из n – k проверочных разрядов в кодирующем устройстве осуществляется посредством сумматоров по модулю два.
На каждый разряд сумматора (кроме первого) используется четыре элемента И (вентиля) и два элемента ИЛИ.
Пример 33. Рассмотрим техническую реализацию кода (7,4), имеющего целью исправление одиночных ошибок.
Правила построения кода определяются равенствами
a1=a3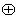
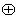
a2=a3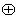
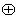
a4=a5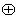
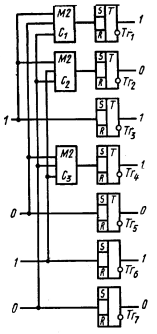
Схема кодирующего устройства приведена на рис. 4.6.
При поступлении импульса синхронизации со схемы управления подлежащая кодированию k-разрядная комбинация неизбыточного кода переписывается, например, с аналого-кодового преобразователя в информационные разряды n-разрядного регистра. Предположим, что в результате этой операции триггеры регистра установились в состояния, указанные в табл. 4.9.
С некоторой задержкой формируются выходные импульсы сумматоров С1, С2 С3, которые устанавливают триггеры проверочных разрядов в положение 0 или 1 в соответствии с приведенными выше равенствами. Например, в нашем случае ко входам сумматора C1 подводится информация, записанная в 3, 5 и 7-разрядах и, следовательно, триггер Тг1 первого проверочного разряда устанавливается в положение 1, аналогично триггер Тг2 устанавливается в положение 0, а триггер Тг4 — в положение 1.
Сформированная в регистре разрешенная комбинация (табл. 4.10) импульсом, поступающим с блока управления, последовательно или параллельно считывается в линию связи. Далее начинается кодирование следующей комбинации.
Рассмотрим теперь схему декодирования и коррекции ошибок (рис. 4.7), строящуюся на основе совокупности проверочных равенств. Для кода (7, 4) они имеют вид:
a2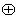
Кодовая комбинация, возможно содержащая ошибку, поступает на n-разрядный приемный регистр (на рис. 4.7 триггеры Тг1 –Тг7). По окончании переходного процесса в триггерах с блока управления на каждый из сумматоров (C1 – С3) поступает импульс опроса.
Технические средства кодирования и декодирования для циклических кодов
4.11 Технические средства кодирования и декодирования для циклических кодов
4.11.1 Линейные переключательные схемы
Основу кодирующих и декодирующих устройств циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю два. Такие регистры также называют многотактными линейными переключательными схемами и линейными кодовыми фильтрами Хаффмена. Они состоят из ячеек памяти, сумматоров по модулю два и устройств умножения на коэффициенты многочленов множителя или делителя. В случае двоичных кодов для умножения на коэффициент, равный 1, требуется только наличие связи в схеме. Если коэффициент равен 0, то связь отсутствует. Сдвиг информации в регистре осуществляется импульсами, поступающими с генератора продвигающих импульсов, который на схеме, как правило, не указывается. На вход устройств поступают только коэффициенты многочленов, причем начиная с коэффициента при переменной в старшей степени.
На рис. 4.9 представлена схема, выполняющая умножение произвольного (например, информационного) многочлена
на некоторый фиксированный (например, образующий) многочлен
Произведение этих многочленов равно
Предполагаем, что первоначально ячейки памяти находятся в нулевом состоянии и что за коэффициентами множимого следует n-k нулей.
На первом такте на вход схемы поступает первый коэффициент аk-1 многочлена а(х) и на выходе появляется первый коэффициент произведения, равный
На следующем такте на выход поступит сумма
т.е. второй коэффициент произведения, и т. д. На n-м такте все ячейки, кроме последней, будут в нулевом состоянии и на выходе получим последний коэффициент а0g0
Используется также схема умножения многочленов при поступлении множимого младшим разрядом вперед (рис. 4.10).
На рис. 4.11 представлена схема, выполняющая деление произвольного многочлена, например
на некоторый фиксированный (например, образующий) многочлен
Обратные связи регистра соответствуют виду многочлена g(x). Количество включаемых в него сумматоров равно числу отличных от нуля коэффициентов g(x), уменьшенному на единицу. Это объясняется тем, что сумматор сложения коэффициентов старших разрядов многочленов делимого и делителя в регистр не включается, так как результат сложения заранее известен (он равен 0).
За первые n-k тактов коэффициенты многочлена-делимого заполняют регистр, причем коэффициент при х в старшей степени достигает крайней правой ячейки. На следующем такте «единица» делимого, выходящая из крайней ячейки регистра, по цепи обратной связи подается к сумматорам по модулю два, что равносильно вычитанию многочлена-делителя из многочлена-делимого. Если в результате предыдущей операции коэффициент при старшей степени х у остатка оказался равным нулю, то на следующем такте делитель не вычитается. Коэффициенты делимого только сдвигаются вперед по регистру на один разряд, что находится в полном соответствии с тем, как это делается при делении многочленов столбиком.
Деление заканчивается с приходом последнего символа многочлена-делимого. При этом разность будет иметь более низкую степень, чем делитель. Эта разность и есть остаток.
Отметим, что если в качестве многочлена-делителя выбран простой многочлен степени m = n-k, то, продолжая делить образовавшийся остаток при отключенном входе, будем получать в регистре по одному разу каждое из ненулевых m-разрядных двоичных чисел. Затем эта последовательность чисел повторяется.
Пример 37. Рассмотрим процесс деления многочлена а(х)х т =(x 3 +1)x 3 на образующий многочлен g(x) = х 3 + х 2 +1. Схема для этого случая представлена на рис. 4.12, где 1, 2, 3-ячейки регистра. Работа схемы поясняется табл. 4.16.
Вычисление остатка начинается с четвертого такта и заканчивается после седьмого такта. Последующие сдвиги приводят к образованию в регистре последовательности из семи различных ненулевых трехразрядных чисел. В дальнейшем эта последовательность чисел повторяется.
Процедура кодирования и декодирования для циклических кодов



Кодирующие и декодирующие устройства циклических кодов
Преобразование комбинации первичного k – разрядного кода в комбинацию циклического (n, k) – кода может быть осуществлено либо при помощи порождающего многочлена g(x), либо при помощи проверочного многочлена h(x).
а) Процедура кодирования для циклического кода по g(x).
Любой циклический (n, k) – код может быть получен в результате следующего процесса. Пусть 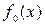
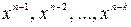
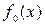
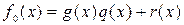
Образуем новый многочлен 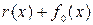
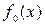
Для полученного многочлена справедливо
и так как его степень не превышает n-1, то по определению 2 циклического кода полученный подобным образом вектор 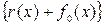
В векторе 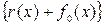
Таким образом, для формирования кодовой комбинации циклического (n, k) – кода по данному способу требуется иметь устройство для умножения комбинации первичного кода, представляемой многочленом 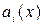
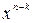
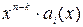
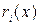
В комбинации циклического (n, k) – кода коэффициенты многочлена 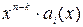
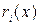
б) Процедура кодирования для циклического кода по h(x).
Для проверочного многочлена h(x) степени k циклического (n, k) – кода справедливо 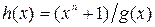
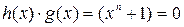
Так как по определению 2 любая кодовая комбинация кратна g(x), то для произвольной комбинации f(x) выполняется 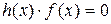
Если принять 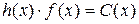
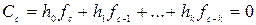
Учитывая, что 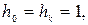
Итак, если известны коэффициенты 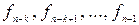
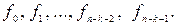
в) Процедура декодирования для циклических кодов
В основе процедуры декодирования лежит процесс выявления принадлежности принятой комбинации к множеству разрешенных кодовых комбинаций. Эта задача решается, как было показано выше, вычислением синдрома для принятой комбинации 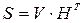
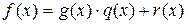
Если остаток от деления r(x)=0, то считают, что комбинация f(x) и была передана.
В этом случае k коэффициентов отдаются потребителю в качестве переданного сообщения.
Если же остаток от деления 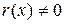
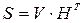
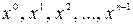
Пример 6.13. Определить принадлежность комбинации 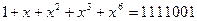

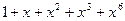


Таким образом, для вычисления синдрома 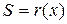
Итак, мы установили существование двух способов вычисления синдрома для кодовых комбинаций. При этом второй способ отражает специфику представления кодовой комбинации в виде многочлена. Возможен ещё и третий способ вычисления синдрома, также вытекающий из представления кодовых комбинаций многочленами. Каждая кодовая комбинация циклического (n,k) кода кратна порождающему многочлену g(x) степени n-k. Это в свою очередь означает, что любая кодовая комбинация имеет среди своих корней n-k корней порождающего многочлена. Значит принадлежность принятой комбинации f(x) к используемому коду можно определить подстановкой вместо формальной переменной x в принятой комбинации корней порождающего многочлена g(x).
Пусть – α i – корень порождающего многочлена (n,k)–кода, а f(x) – кодовая комбинация этого кода, тогда должно быть справедливо: f(x=α i )=0 для всех значений i, определяющих корни g(x).
Выше отмечалось, что синдром должен определять вид ошибок, появившихся в кодовой комбинации при передаче её по каналу с помехами.
Пусть передана комбинация f(x), а принята комбинация f'(x)=f(x)+e(x), где e(x) – многочлен ошибок. Тогда f'(x=α i )=f(x=α i )+e(x=α i )=e(x=α i )=Si
2.Если e(x) по виду совпадает с одной из кодовых комбинаций, то Si=e(x=α i )=0,
т.е. имеет место нулевой синдром, который приведёт к необнаруженной ошибке. Если же e(x) отличается от кодовой комбинации, то синдром будет ненулевым: Si=e(x=α i )≠0 и ошибка будет выявлена.
Пример 6.13. (продолжение)
Покажем, что нахождение синдрома для проверки принадлежности комбинации f(x)=1+x+x 2 +x 3 +x 6 =1111001 циклическому(7,4) – коду с g(x) = 1+x+x 3 может быть осуществлено подстановкой корней многочлена g(x) вместо x в f(x).
Для этого обратимся к процедуре к процедуре умножения:
Обратим внимание, что матрица H T (7,4)- кода в точности соответствует представлению элементов GF(2 3 ) в виде ненулевых векторов в таблице задачи 6 раздела 5.8. Это не случайное совпадение. Обе эти совокупности двоичных последовательностей длины 3 получены как классы вычетов многочленов по модулю одного и того же многочлена 3-ей степени и отображают одну и ту же циклическую группу.
При этом процедура замены в проверяемом многочлене x i на α i и последующего суммирования результатов замены полностью эквивалентна сложению строк матрицы H T соответствующим «1» в двоичном представлении многочлена.
Использование всех корней порождающего многочлена для формирования элементов синдрома, будут реализовано ниже в связи с понятием синдромный многочлен.
В случае исправления ошибок необходима еще и схема сопоставления синдрома образцу ошибки. В простейшем случае при исправлении однократных ошибок в основе этой схемы лежит генератор элементов поля GF(2 m ).