теорема шеннона о кодировании источника
Основная теорема Шеннона о кодировании для канала без помех
1. При любой производительности источника сообщений, меньшей пропускной способности канала, существует способ кодирования, позволяющий передавать по каналу все сообщения, вырабатываемые источником.
2. Не существует способа кодирования, обеспечивающего передачу сообщений без их неограниченного накопления, если производительность источника сообщений больше пропускной способности канала.
Кодирование, о котором идет речь в этой формулировке, называется эффективным(безызбыточным) кодированием.
Пример эффективного кода
Энтропия множества сообщений – H(X) = 2,76 бит.
Максимальная энтропия источника – Hmax= 3,00 бит.
Основная теорема Шеннона о кодировании для канала с помехами
1. При любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником, со сколь угодно малой вероятностью ошибки.
2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.
Здесь речь идет о помехоустойчивом кодировании. Помехоустойчивость достигается за счет специальным образом введеннойизбыточности. Это означает, что количество возможных кодовых комбинаций в коде превышает количество сообщений, которые требуется представить (закодировать) в коде. При этом можно построить коды, обнаруживающие ошибки заданной кратности, исправляющие ошибки заданной кратности, а также и то, и другое вместе. Простейшим кодом, обнаруживающим одиночные ошибки, является код спроверкой на четность (добавляется один дополнительный разряд таким образом, чтобы общее число единиц в каждой кодовой комбинации было четным).
Пример помехоустойчивого кода
Исходный неизбыточный код
Помехоустойчивый избыточный код с проверкой на чётность
000
1. Первая теорема Шеннона. Основные понятия
Теория кодирования информации является одним из разделов теоретической информатики. К основным задачам, решаемым в данном разделе, необходимо отнести следующие:
Для представления дискретных сообщений используется некоторый алфавит. Однако однозначное соответствие между содержащейся в сообщении информацией и его алфавитом отсутствует.
В целом ряде практических приложений возникает необходимость перевода сообщения хода из одного алфавита к другому, причем, такое преобразование не должно приводить к потере информации.
Код — (1) правило, описывающее соответствие знаков или их сочетаний первичного алфавита знакам или их сочетаниям вторичного алфавита.
(2) набор знаков вторичного алфавита, используемый для представления знаков или их сочетаний первичного алфавита.
Кодирование — перевод информации, представленной сообщением в первичном алфавите, в последовательность кодов.
Декодирование — операция, обратная кодированию, т.е. восстановление информации в первичном алфавите по полученной последовательности кодов.
Кодер — устройство, обеспечивающее выполнение операции кодирования.
Декодер — устройство, производящее декодирование.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо ее потерь.
Не обсуждая технических сторон передачи и хранения сообщения (т.е. того, каким образом фактически реализованы передача-прием последовательности сигналов или фиксация состояний), дается математическая постановка задачи кодирования.
смысл которого в том, что операция обратимого кодирования может увеличить количество информации в сообщении, но не может его уменьшить. Однако каждая из величин в данном неравенстве может быть заменена произведением числа знаков на среднее информационное содержание знака, т.е.:
Как следует из (3.4), минимально возможным значением средней длины кода будет:
Первая теорема Шеннона, которая называется основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:
При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак первичного алфавита, будет сколь угодно близко к отношению средних информации на знак первичного и вторичного алфавитов.
Из (3.5) видно, что имеются два пути сокращения К min (А,В):
В качестве меры превышения К(А,В) над K min (А,В) можно ввести относительную избыточность кода (Q(А,В):
Данная величина показывает, насколько операция кодирования увеличила длину исходного сообщения. Очевидно, Q(A,B) → 0 при К(А,В) → К min (А,В). Следовательно, решение проблемы оптимизации кода состоит в нахождении таких схем кодирования, которые обеспечили бы приближение средней длины кода к значению К min (А,В), равному отношению средних информации на знак первичного и вторичного алфавитов. Чем меньше Q(A,B), тем Ifin(В) ближе к Ist(A)), т.е. возникает меньше информации, связанной с кодированием, более выгодным оказывается код и более эффективной операция кодирования.
Используя понятие избыточности кода, можно построить иную формулировку теоремы Шеннона:
При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
и первая теорема Шеннона получает следующую интерпретацию:
При отсутствии помех средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
Применение формулы (3.7) для двоичных сообщений источника без памяти при кодировании знаками равной вероятности дает:
При декодировании двоичных сообщений возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) кодовых слов (групп элементарных сигналов), соответствующих отдельным знакам первичного алфавита. При этом приемное устройство фиксирует интенсивность и длительность сигналов, а также может соотносить некоторую последовательность сигналов с эталонной (таблицей кодов).
Возможны следующие особенности вторичного алфавита, используемого при кодировании:
Комбинации перечисленных особенностей определяют основу конкретного способа кодирования, однако, даже при одинаковой основе возможны различные варианты построения кодов, отличающихся своей эффективностью.
Теория кодирования. Кодирование источника. Посимвольное кодирование
Теория кодирования изучает свойства различных кодов и их применимость в конкретных задачах.
В рамках теории кодирования, кодом называется некое правило (алгоритм), которое однозначно ставит неким словам над исходным алфавитом некие новые кодовые слова, возможно над другим, целевым, алфавитом.
Код Пусть \(S\) и \(T\) – конечные множества, называемые соответственно исходным и целевым алфавитами. Код \(C: S^* \to T^*\) есть всюду определённая функция, отображающая элементы \(S^*\) – слова (последовательностей символов) над исходным алфавитом – на элементы множества \(T^*\) – слова над целевым алфавитом.
В соответствии с исследуемыми задачами, выделяют четыре различных направления в теории кодирования:
Сжатие данных
Сжатие данных в общем случае – это представление информации в меньшем информационном объёме, чем исходные данные. Выделяют сжатие данных без потерь (lossless) и сжатие данных с потерями (lossy).
Сжатие данных без потерь позволяет в точности восстановить исходный сигнал. Сжатие данных с потерями позволяет восстановить некую “достаточно хорошую” аппроксимацию исходного сигнала.
Модель сжатия без потерь:
В качестве меры “успешности” сжатия без потерь вводится коэффициент сжатия: \[r = \frac
Модель сжатия с потерями:
Кроме требования однозначности, как правило, требуется так же обеспечить возможность каким-то образом разделять кодовые слова, соответствующие различным исходным сообщениям. Для достижения этого могут использоваться следующие подходы:
Определение энтропии так же даёт нам некоторые указания касательно свойств оптимального кода, исходя из того, что энтропия кодированного сигнала должна быть максимальна (т.е. количество информации на символ кода – максимально):
Наиболее экономным для большинства применений оказывается использование префиксных кодов.
Предел оптимального кодирования без потерь нам даёт теорема Шеннона о кодировании источника: средняя (в смысле теории вероятностей) длина кодового слова не может быть меньше энтропии источника.
Основные методы посимвольного кодирования
Посимвольное кодирование, или кодирование без памяти, является простейшим методом кодирования.
Понятно, что, по крайней мере в случае кодирования без потерь, код должен быть однозначно декодируемым.
Мы так же хотим, чтобы средний (ожидаемый) информационный объем кода был минимальный.
Ожидаемая длина кодового слова (средняя длина кода) Математическое ожидание длины кодового слова из кода \(C\) над источником \(X\) обозначается \(L(C, X)\) и называется ожидаемой (средней) длиной кодового слова: \[L(C,X) = \sum_
Необходимое и достаточное условие существования однозначно декодируемых префиксных кодов (и вообще однозначно декодируемых кодов переменной длины) устанавливается неравенством Крафта-МакМиллана:
Теорема (неравенство Крафта-МакМиллана) Пусть каждый символ исходного алфавита \(S=\
Пусть \(S = \sum_i r^<-l_i>.\) Рассмотрим число \[S^N = \sum_
l_i,\) \(l_
Теорема Шеннона о кодировании источника ограничивает снизу максимально достижимое сжатие энтропией источника. Сохраняется ли это ограничение при посимвольном кодировании? Вообще говоря, ответ может быть неочевиден. Поэтому, найдём нижнюю границу ожидаемой длины кода \(L(C, X).\) Сперва докажем неравенство Гиббса.
Для упрощения выкладок, без ограничения общности, положим двоичный целевой алфавит. Упрощение достигается за счёт того, что информационный объем кодового слова в битах в таком случае численно совпадает с его длиной.
Это важный результат, поэтому повторимся.
Верно так же и обратное: любой выбор длин кодовых слов неявно определяет оптимальный источник.
Оптимальный источник для посимвольного кодера \(C\)
Определяется распределением вероятностей \[P(x) = \frac<2^<-|C(x)|>> <\sum_
Мы установили нижнюю границу. Но насколько близко к ней можно подойти? Оказывается, в пределах одного бита.
\(\Delta\) : Первое неравенство \(L(C,X) \ge H(X)\) уже доказано выше.
Алгоритм Хаффмана
Один из способов построить оптимальный посимвольный код – алгоритм Хаффмана.
Более подробное описание доступно здесь
Код, составленный по алгоритму Хаффмана, оптимален.
Тогда, поскольку \(X’\) отличается от \(X\) тем, что два символа из \(X\) в нём отождествляются, а отождествлённый символ в наших кодах имеет кодовое слово на 1 бит короче, имеем \[L = L’ + P(x’),\] \[\hat L = \hat L’ + P(x’).\]
По индукции, код Хаффмана для любого алфавита размерности \(|X|\ge 2\) оптимален.
Другие алгоритмы посимвольного кодирования
Код Шеннона
Код Шеннона использовался Шенноном при доказательстве теоремы о кодировании источника, однако он не является оптимальным, и никогда не лучше (но иногда эквивалентен) коду Шеннона-Фано.
Код Шеннона-Фано
Все символы алфавита источника упорядочиваются по убыванию вероятности. Полученный массив делится на две непрерывные части, максимально близкие по сумме вероятностей входящих в них символов. Одной из этих частей присваивается метка “0”, второй – метка “1”. Алгоритм рекурсивно повторяется для каждой из частей, пока не дойдёт до единственного символа. Кодом этого символа является последовательность меток частей.
Следует отметить, что подход похож на подход Хаффмана, однако алгоритм Хаффмана строит дерево “снизу вверх”, от листьев, в то время как алгоритм Шеннона-Фано строит дерево “сверху вниз”, от корня.
Код Элиаса (Шеннона-Фано-Элиаса)
Так же известен как код Гильберта-Мура 1
Каждому символу ставится в соответствие число \[F_i = \frac
Gilbert E. N., Moore E. F. Variable‐Length Binary Encodings //Bell System Technical Journal. – 1959. – Т. 38. – №. 4. – С. 933-967.↩︎
Теорема шеннона о кодировании источника
Первая теорема Шеннона о передаче информации, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:
При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.
Используя понятие избыточности кода, можно дать более короткую формулировку теоремы:
При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
Данные утверждения являются теоремами и, следовательно, должны доказываться, однако доказательства мы опустим. Для нас важно, что теорема открывает принципиальную возможность оптимального кодирования. Однако необходимо сознавать, что из самой теоремы никоим образом не следует, как такое кодирование осуществить практически – для этого должны привлекаться какие-то дополнительные соображения, что и станет предметом нашего последующего обсуждения.
I1 (A)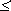 
K (2)
и первая теорема Шеннона получает следующую интерпретацию:
При отсутствии помех передачи средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
Применение формулы (2) для двоичного кодирования дает:
Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей). При этом возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов. Приемное устройство фиксирует интенсивность и длительность сигналов. Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности. Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код). Наконец, коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов). В результате при кодировании (алфавитном и словесном) возможны следующие варианты сочетаний:
В случае использования неравномерного кодирования или сигналов разной длительности (ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).
Длительность двоичного элементарного импульса (
) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время 
. Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
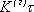
Теорема Шеннона
Теорема Шеннона — Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временно́го аналогового канала коммуникаций, искажённого гауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанной полосой пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и гауссовский шум характеризуется известной мощностью или мощностью спектральной плотности. Закон назван в честь Клода Шеннона и Ральфа Хартли.
Содержание
Утверждение теоремы
Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона — Хартли утверждает, что пропускная способность канала 
, означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала 
через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности 
равна:
— пропускная способность канала, бит/с; 
— полоса пропускания канала, Гц; — полная мощность сигнала над полосой пропускания, Вт или В²; — полная шумовая мощность над полосой пропускания, Вт или В²; 
— частное от деления отношения сигнала к его шуму (SNR) на гауссовский шум, выраженное как отношение мощностей.
История развития
В течение конца 1920-х гг. Гарри Найквист и Ральф Хартли разработали фундаментальные идеи, связанные с передачей информации, с помощью телеграфа как системы коммуникаций. В то время, это был прорыв, но науки как таковой не существовало. В 1940-х гг., Клод Шеннон ввёл понятие пропускной способности канала, которое базировалось на идеях Найквиста и Хартли, а затем сформулировал полную теорию передачи информации.
Критерий Найквиста
В 1927 году Найквист установил, что число независимых импульсов в единицу времени, которые могут быть переданы через телеграфный канал, ограничено удвоенной максимальной частотой пропускания канала (этой частоте соответствует чередующаяся последовательность нулей и единиц, остальные комбинации сигналов соответствуют более низким частотам)
где 
— частота импульса (имп/с), и — полоса пропускания (Гц).
Формула Хартли
Теоремы Шеннона для канала с шумами
Теоремы Шеннона для канала с шумами (теоремы Шеннона для передачи по каналу с шумами) связывают пропускную способность канала передачи информации и существование кода, который возможно использовать для передачи информации по каналу с ошибкой, стремящейся к нулю (при увеличении длины блока).
Если скорость передачи сообщений меньше пропускной способности канала связи
то существуют коды и методы декодирования такие, что средняя и максимальная вероятности ошибки декодирования стремятся к нулю, когда длина блока стремится к бесконечности.
C,» border=»0″ />
то кода, на основе которого можно добиться сколько угодной малой вероятности возникновения ошибки, не существует.
Теорема Шеннона — Хартли
В данной теореме определено, что достичь максимальной скорости (бит/с) можно путем увеличения полосы пропускания и мощности сигнала и, в то же время, уменьшения шума.
Теорема Шеннона — Хартли ограничивает информационную скорость (бит/с) для заданной полосы пропускания и отношения «сигнал/шум». Для увеличения скорости необходимо увеличить уровень полезного сигнала, по отношению к уровню шума.
Если бы существовала бесконечная полоса пропускания, бесшумовой аналоговый канал, то можно было бы передать неограниченное количество безошибочных данных по ней за единицу времени. Реальные каналы имеют ограниченные размеры и в них всегда присутствует шум.
Удивительно, но не только ограничения полосы пропускания влияют на количество передаваемой информации. Если мы комбинируем шум и ограничения полосы пропускания, мы действительно видим, что есть предел количества информации, которую можно было передать, даже используя многоуровневые методы кодирования. В канале, который рассматривает теорема Шеннона — Хартли, шум и сигнал дополняют друг друга. Таким образом, приёмник воспринимает сигнал, который равен сумме сигналов, кодирующего нужную информацию и непрерывную случайную, которая представляет шум.
Это дополнение создает неуверенность относительно ценности оригинального сигнала. Если приёмник обладает информацией о вероятности ненужного сигнала, который создает шум, то можно восстановить информацию в оригинальном виде, рассматривая все возможные влияния шумового процесса. В случае теоремы Шеннона — Хартли шум, как таковой, произведен гауссовским процессом с некоторыми отклонениями в канале передачи. Такой канал называют совокупным белым гауссовским шумовым каналом, так как гауссовский шум является частью полезного сигнала. «Белый» подразумевает равное количество шума во всех частотах в пределах полосы пропускания канала. Такой шум может возникнуть при воздействии случайных источников энергии, а также быть связан с ошибками, возникшими при кодировании. Зная о вероятности возникновения гауссовского шума, значительно упрощается определение полезного сигнала.
Значение теоремы
Пропускная способность канала и формула Хартли
Сравнивая пропускную способность канала и формулу Хартли, мы можем найти эффективное число 
различимых уровней:
Взятие квадратного корня по сути возвращает отношение мощностей к отношению напряжений, таким образом число уровней приблизительно равно отношению среднеквадратичной амплитуды сигнала к шумовому стандартному отклонению. Это подобие в форме между пропускной способностью по Шеннону и формулой Хартли не стоит понимать буквально, что для безошибочной передачи достаточно уровней сигнала. Избыточное кодирование для устранения ошибок потребует большего числа уровней, но предельная скорость передачи данных, к которой можно приблизиться с кодированием, эквивалентна использованию того самого из формулы Хартли.