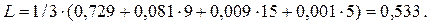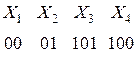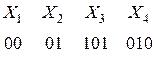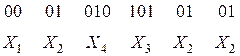эффективное кодирование дискретных сообщений
Эффективное кодирование дискретных сообщений
4.3. Эффективное кодирование дискретных сообщении
* ( В этом параграфе предполагается, что последовательность кодовых символов принимается без ошибок. Поэтому рассматриваемую ниже теорему часто называют теоремой кодирования для канала без помех. )
Но отношение (4.27) представляет среднее число кодовых символов, приходящихся на одно элементарное сообщение. Таким образом, для возможности кодирования и однозначного декодирования сообщения необходимо, чтобы среднее число двоичных символов на сообщение было не меньше энтропии Н (А). Является ли это условие достаточным?
Одна из основных теорем теории информации утверждает, что юно «почти достаточно». Точнее, содержание теоремы кодирования для источника заключается в том, что, передавая двоичные символы со скоростью vK, симв./с, можно закодировать сообщения так, чтобы передавать их со скоростью
Таким же образом можно закодировать сообщения любого источника с объемом алфавита К, затрачивая υ0 = log K двоичных символов на элементарное сообщение. Если, однако, сообщения передаются не равновероятно, и (или) не независимо, то H(A) 5 ) и они передаются равновероятно и независимо, то Н(А) = 5 бит. Каждую букву можно закодировать последовательностью из пяти двоичных символов, поскольку существует 32 такие последовательности. Разумеется, таким же равномерным кодом можно закодировать и буквы в связном русском тексте, и именно так часто поступают на практике. Но можно обойтись значительно меньшим числом символов на букву. Как указывалось выше, для русского литературного текста Н(A) m 1,5 бит и, следовательно, возможен способ эффективного кодирования (или кодирования со сжатием сообщения), при котором в среднем на букву русского текста будет затрачено немногим более 1,5 двоичных символа, т. е. на 70% меньше, чем при примитивном коде.
Существует довольно много способов сжатия сообщений или сокращения избыточности текста. Так, напр, эта фр. напис. сок-ращ. и тем не м. мож. надеят., что чит-ль пойм, ее прав. В предыдущей фразе удалось уменьшить число букв (а следовательно и символов, если ее кодировать равномерным кодом) почти на. 40%.
Другая возможность заключается в том, чтобы кодировать не- отдельные буквы, а целые слова. В достаточно большом словаре имеется около 10 000 слов, содержащих в среднем по 7 букв. Считая, что в среднем каждое слово может иметь 3 грамматические формы, нам придется закодировать около 30 000 типичных слов. Если применить равномерный код, то на каждое слово придется затратить 15 двоичных символов (2 15 = 32 768). Таким образом, а среднем на букву придется немногим больше двух символов, т. е. сжатие достигнет почти 60% вместо теоретических 70%. Слова, не вошедшие в словарь, придется передавать обычным способом, затрачивая пять символов на букву. Но поскольку такие нетипичные слова будут встречаться крайне редко, это не внесет заметной поправки в общий баланс.
На основании изложенной теоремы можно сформулировать такое свойство энтропии: энтропия источника совпадает с тем минимальным количеством информации, которое при надлежащем кодировании необходимо передать по каналу без помех для того, чтобы сколь угодно точно восстановить это сообщение. Чем выше требуемая точность восстановления сообщения, тем сложнее, в общем случае, должно быть кодирование.
Интересно отметить одно свойство эффективного кода. Так как код должен передавать всю собственную информацию источника Н(А) при наименьшей скорости v, то очевидно, что сама последовательность кодовых символов по возможности не должна иметь избыточности. Это значит, что все символы эффективного кода передаются почти равновероятно и вероятность появления любого символа мало зависит от предыдущих и последующих символов.
Эффективное кодирование дискретных сообщений
Основы передачи дискретных сообщений
Тема 4. Эффективное (статическое) кодирование
Эффективное кодирование – это процедуры направленные на устранение избыточности.
Основная задача эффективного кодирования – обеспечить, в среднем, минимальное число двоичных элементов на передачу сообщения источника. В этом случае, при заданной скорости модуляции обеспечивается передача максимального числа сообщений, а значит максимальная скорости передачи информации.
Пусть имеется источник дискретных сообщений, алфавит которого 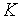
При кодировании сообщений данного источника двоичным, равномерным кодом, потребуется 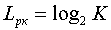
Если вероятности 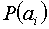
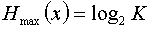
В данном случае каждое сообщение источника имеет информационную емкость 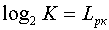
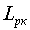
Если при том же объеме алфавита сообщения не равновероятны, то, как известно, энтропия источника будет меньше
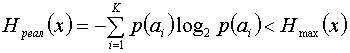
Если и в этом случае использовать для перевозки сообщения 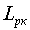
Появляется избыточность, которая может быть определена по следующей формуле
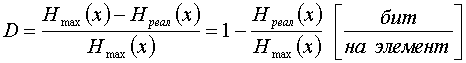
Среднее количество информации, приходящееся на один двоичный элемент комбинации при кодировании равномерным кодом
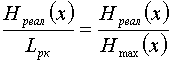
Для кодирования 32 букв русского алфавита, при условии равновероятности, нужна 5 разрядная кодовая комбинация. При учете ВСЕХ статистических связей реальная энтропия составляет около 1,5 бит на букву. Нетрудно показать, что избыточность в данном случае составит
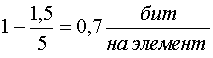
Если средняя загрузка единичного элемента так мала, встает вопрос, нельзя ли уменьшить среднее количество элементов необходимых для переноса одного сообщения и как наиболее эффективно это сделать?
Для решения этой задачи используются неравномерные коды.
При этом, для передачи сообщения, содержащего большее количество информации, выбирают более длинную кодовую комбинацию, а для передачи сообщения с малым объемом информации используют короткие кодовые комбинации.
Учитывая, что объем информации, содержащейся в сообщении, определяется вероятностью появления
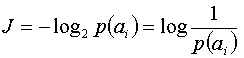
Для сообщения, имеющего высокую вероятность появления, выбирается более короткая комбинация и наоборот, редко встречающееся сообщение кодируется длинной комбинацией.
Т.о. на одно сообщение будет затрачено в среднем меньшее единичных элементов 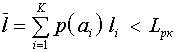
Если скорость телеграфирования постоянна, то на передачу одного сообщения будет затрачено в среднем меньше времени
А значит, при той же скорости телеграфирования будет передаваться большее число сообщений в единицу времени, чем при равномерном кодировании, т.е. обеспечивается большая скорость передачи информации.
Каково же в среднем минимальное количество единичных элементов требуется для передачи сообщений данного источника?
Ответ на этот вопрос дал Шеннон.
Шеннон показал, что
1. Нельзя закодировать сообщение двоичным кодом так, что бы средняя длина кодового слова 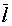
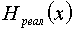
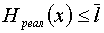
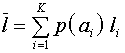
2. Существует способ кодирования, при котором средняя длина кодового слова немногим отличается от энтропии источника
Остается выбрать подходящий способ кодирования.
Эффективность применения оптимальных неравномерных кодов может быть оценена:
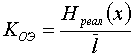
В неравномерных кодах возникает проблема разделения кодовых комбинаций. Решение данной проблемы обеспечивается применением префиксных кодов.
Префиксным называют код, для которого никакое более короткое слово не является началом другого более длинного слова кода. Префиксные коды всегда однозначно декодируемы.
Веедем понятие кодового дерева для множества кодовых слов.
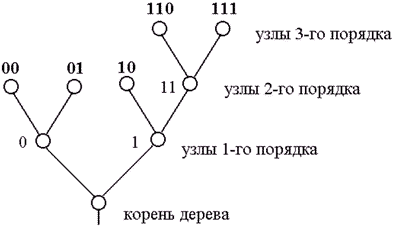
Наглядное графическое изображение множества кодовых слов можно получить, установив соответствие между сообщениями и концевыми узлами двоичного дерева. Пример двоичного кодового дерева изображен на рисунке. 1.
Рисунок 1. Пример двоичного кодового дерева
Две ветви, идущие от корня дерева к узлам первого порядка, соответствуют выбору между “0” и “1” в качестве первого символа кодового слова: левая ветвь соответствует “0”, а правая – “1”. Две ветви, идущие из узлов первого порядка, соответствуют второму символу кодовых слов, левая означает “0”, а правая – “1” и т. д. Ясно, что последовательность символов каждого кодового слова определяет необходимые правила продвижения от корня дерева до концевого узла, соответствующего рассматриваемому сообщению.
Формально кодовые слова могут быть приписаны также промежуточным узлам. Например, промежуточному узлу второго порядка на рис.1 можно приписать кодовое слово 11, которое соответствует первым двум символам кодовых слов, соответствующих концевым узлам, порождаемых этим узлом. Однако кодовые слова, соответствующие промежуточным узлам, не могут быть использованы для представления сообщений, так как в этом случае нарушается требование префиксности кода.
Требование, чтобы только концевые узлы сопоставлялись сообщениям, эквивалентно условию, чтобы ни одно из кодовых слов не совпало с началом (префиксом) более длинного кодового слова.
Любой код, кодовые слова которого соответствуют различным концевым вершинам некоторого двоичного кодового дерева, является префиксным, т. е. однозначно декодируемым.
Одним из часто используемых методов эффективного кодирования является так называемый код Хаффмена.
Пусть сообщения входного алфавита 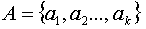
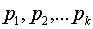
Тогда алгоритм кодирования Хаффмена состоит в следующем:
1. Сообщения располагаются в столбец в порядке убывания вероятности их появления.
2. Два самых маловероятных сообщения объединяем в одно сообщение 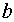
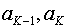
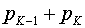
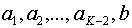
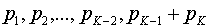
3. Повторяем шаги 1 и 2 до тех пор, пока не получим единственное сообщение, вероятность которого равна 1.
На основании полученной таблицы можно построить кодовое дерево
Так как в процессе кодирования сообщениям сопоставляются только концевые узлы, полученный код является префиксным и всегда однозначно декодируем.
При равномерных кодах одиночная ошибка в кодовой комбинации приводит к неправильному декодированию только этой комбинации. Одним из серьёзных недостатков префиксных кодов является появление трека ошибок, т.е. одиночная ошибка в кодовой комбинации, при определенных обстоятельствах, способна привести к неправильному декодированию не только данной, но и нескольких последующих кодовых комбинаций.
Пример на однозначность декодирования и трек ошибок
Пусть передавалась следующая последовательность
При возникновении ошибки в первом двоичном элементе, получим
0 0 0 1 1 1 0 0 0 1
Т.О. ошибка в одном разряде комбинации первого символа привела к неправильному декодированию двух символов. (Трек ошибок).
Эффективное кодирование дискретных сообщений
Основы передачи дискретных сообщений
Лабораторная работа «Коды Хаффмана»
Изучение принципа эффективного кодирования источника дискретных сообщений.
Таблица 1 Вероятности появления сообщений алфавита
Вариант для построения кода определяется по последней цифре пароля. При N>7 номер варианта равен N-7. Если N=0, то вариант 3.
К числу основных информационных характеристик источника сообщений относятся: количество информации в отдельных сообщениях, энтропия и производительность источника сообщений.
Среднее количество информации, выдаваемое источником в единицу времени, называют производительностью источника и определяют по формуле:
где Т – среднее время, отводимое на передачу одного сообщения.
Выражение для средней длительности сообщения имеет вид
Код 2 декодируется однозначно, поскольку все кодовые комбинации этого кода имеют равные длины и различны.
Код 3 также однозначно декодируемый, поскольку никакая его кодовая комбинация не является началом (префиксом) другой кодового слова.
Код, обладающий тем свойством, что никакая более короткая комбинация не является началом другой более длинной комбинации кода, называют префиксным. Префиксные коды всегда однозначно декодируемы.
Кодовое дерево для множества кодовых слов.
Рисунок 1. Пример двоичного кодового дерева
Наглядное графическое изображение множества кодовых комбинаций можно получить, установив соответствие между сообщениями и концевыми узлами двоичного дерева. Пример двоичного кодового дерева изображен на рисунке 1.
Две ветви, идущие от корня дерева к узлам первого порядка, соответствуют выбору между “0” и “1” в качестве первого двоичного символа кодовой комбинации: левая ветвь соответствует “0”, а правая – “1”. Две ветви, идущие из узлов первого порядка, соответствуют второму символу кодовых комбинаций, левая означает “0”, а правая – “1” и т. д. Ясно, что последовательность символов каждой кодовой комбинации определяет необходимые правила продвижения от корня дерева до концевого узла, соответствующего рассматриваемому сообщению.
Формально кодовые комбинации могут быть приписаны также промежуточным узлам. Например, промежуточному узлу второго порядка на рисунке 1 можно приписать комбинацию 11, которая соответствует первым двум символам кодовых комбинаций, соответствующих концевым узлам, порождаемых этим узлом. Однако кодовые комбинации, соответствующие промежуточным узлам, не могут быть использованы для представления сообщений, так как в этом случае нарушается требование префиксности кода.
Требование, чтобы только концевые узлы сопоставлялись сообщениям, и обеспечивает условие при котором ни одна из кодовых комбинаций не совпадает с началом (префиксом) более длинной кодовой комбинации. Любой код, кодовые комбинации которого соответствуют различным концевым вершинам некоторого двоичного дерева, является префиксным, т. е. однозначно декодируемым.
На рисунке 2 изображены кодовые деревья, соответствующие кодам 2 и 3 (см. таблицу 2).
Рисунок 2 Кодовые деревья для кодов 2 (а) и 3 (б)
Известно, что нельзя закодировать сообщение двоичным кодом таким образом, чтобы средняя длина кодовых комбинаций была меньше, чем величина энтропии источника сообщений, т.е.
Тогда алгоритм кодирования Хаффмена состоит в следующем:
Так как в процессе кодирования сообщениям сопоставляются только концевые узлы, полученный код (код Хаффмена) является префиксным и следовательно всегда однозначно декодируемым.
В данной работе рекомендуется обозначать “1” ветвь идущую от узла в сторону сообщения с большей вероятностью появления.
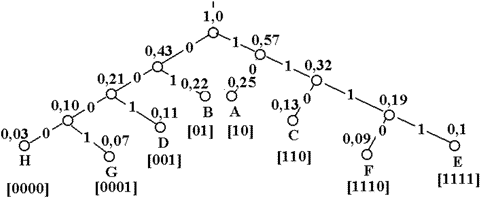
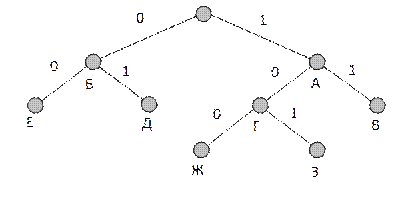
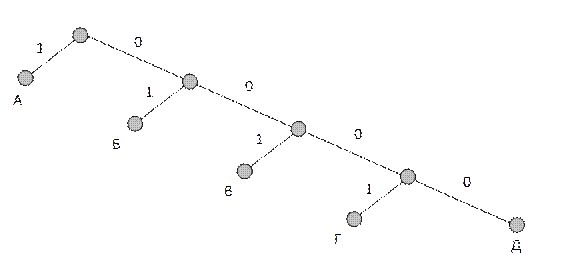
Построение кода Хаффмена для восьми сообщений, появляющихся с вероятностями 0,2; 0,2; 0,15; 0,13; 0,12; 0,1; 0,07; 0,03, иллюстрируется рисунками 3 и 4.
Рисунок 4 Кодовое дерево
Из таблицы 4 видно, что полученный код является неравномерным, причем сообщению с максимальной вероятностью появления соответствует минимальная длительность кодовой комбинации (2 ), а сообщению с минимальной вероятностью – максимальная (4 ).
Эффективное кодирование
Сообщения, передаваемые с использованием систем связи (речь, музыка, телевизионные изображения и т.д.) в большинстве своем предназначены для непосредственного восприятия органами чувств человека и обычно плохо приспособлены для их эффективной передачи по каналам связи. Поэтому они в процессе передачи, как правило, подвергаются кодированию.
Что такое кодирование и зачем оно используется?
Под кодированием в общем случае понимают преобразование алфавита сообщения A< xi >, ( i = 1,2…K ) в алфавит некоторым образом выбранных кодовых символов Â < A<xj >, (j = 1,2…N).
Кодирование сообщений может преследовать различные цели. Например, это кодирование с целью засекречивания передаваемой информации. При этом элементарным сообщениям xi из алфавита A<xi >ставятся в соответствие последовательности, к примеру, цифр или букв из специальных кодовых таблиц, известных лишь отправителю и получателю информации.
Другим примером кодирования может служить преобразование дискретных сообщений xi из одних систем счисления в другие (из десятичной в двоичную, восьмеричную и т. п., из непозиционной в позиционную, преобразование буквенного алфавита в цифровой и т. д.).
Кодирование в канале, или помехоустойчивое кодирование информации, может быть использовано для уменьшения количества ошибок, возникающих при передаче по каналу с помехами.
Наконец, кодирование сообщений может производиться с целью сокращения объема информации и повышения скорости ее передачи или сокращения полосы частот, требуемых для передачи. Такое кодирование называют экономным, безызбыточным, или эффективным кодированием, а также сжатием данных. В данном разделе будет идти речь именно о такого рода кодировании. Процедуре кодирования обычно предшествуют (и включаются в нее) дискретизация и квантование непрерывного сообщения x(t), то есть его преобразование в последовательность элементарных дискретных сообщений <xiq>.
Прежде чем перейти к вопросу экономного кодирования, кратко поясним суть самой процедуры кодирования.
Любое дискретное сообщение xi из алфавита источника A <xi >объемом в Kсимволов можно закодировать последовательностью соответствующим образом выбранных кодовых символов xj из алфавита Â<xj >.
Например, любое число (а xi можно считать числом) можно записать в заданной позиционной системе счисления следующим образом:
где X – основание системы счисления; a0 … an-1 – коэффициенты при имеющие значение от 0 до X –1.
Пусть, к примеру, значение xi = 59 , тогда его код по основанию X = 8, будет иметь вид
Код того же числа, но по основанию X = 4 будет выглядеть следующим образом:
Наконец, если основание кода X = 2, то
Таким образом, числа 73, 323 и 111011 можно считать, соответственно, восьмеричным, четверичным и двоичным кодами числа M = 59.
В принципе основание кода может быть любым, однако наибольшее распространение получили двоичные коды, или коды с основанием 2, длякоторых размер алфавита кодовых символов Â< xj >равен двум, xj Ì 0,1.Двоичные коды, то есть коды, содержащие только нули и единицы, очень просто формируются и передаются по каналам связи и, главное, являются внутренним языком цифровых ЭВМ, т. е. без всяких преобразований могут обрабатываться цифровыми средствами. Поэтому, когда речь идет о кодировании и кодах, чаще всего имеют в виду именно двоичные коды. В дальнейшем будем рассматривать в основном двоичное кодирование.
Самым простым способом представления или задания кодов являются кодовые таблицы, ставящие в соответствие сообщениям xi соответствующие им коды (табл. 7.1).
Соответствие кодовых комбинаций сообщения
| Буква xi | Число xi | Код с основанием 10 | Код с основанием 4 | Код с основанием 2 |
| А | ||||
| Б | ||||
| В | ||||
| Г | ||||
| Д | ||||
| Е | ||||
| Ж | ||||
| З |
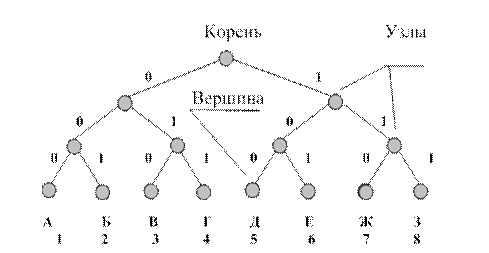
Код, полученный с использованием кодового дерева, изображенного на рис. 7.1, является равномерным трехразрядным кодом.
Рис. 7.1. Графическое представление кодового дерева
Равномерные коды очень широко используются в силу своей простоты и удобства процедур кодирования-декодирования: каждой букве – одинаковое число бит; принял заданное число бит – ищи в кодовой таблице соответствующую букву.
Кодовое дерево для неравномерного кодирования может выглядеть, например, так, как показано на рис. 7.2.
Рис. 7.2. Кодовое дерево для неравномерного кодирования
Однако можно построить неравномерные неприводимые коды, допускающие однозначное декодирование. Для этого необходимо, чтобы всем буквам алфавита соответствовали лишь вершины кодового дерева, например, такого, как показано на рис. 7.3. Здесь ни одна кодовая комбинация не является началом другой, более длинной, поэтому неоднозначности декодирования не будет. Такие неравномерные коды называются префиксными.
Рис. 7.3. Кодовое дерево для префиксного кода
Зачем же используются неравномерные коды, если они столь неудобны?
Рассмотрим пример кодирования сообщений xi из алфавита объемом K= 8с помощью произвольного n-разрядного двоичного кода.
Пусть источник сообщения выдает некоторый текст с алфавитом от Адо З и одинаковой вероятностью букв Р(xi )= 1/8.
Кодирующее устройство кодирует эти буквы равномерным трехразрядным кодом (см. табл. 7.1).
Определим основные информационные характеристики источника с таким алфавитом:
– энтропия источника 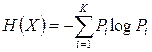
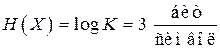
– избыточность источника 
– среднее число символов в коде 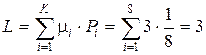
– избыточность кода 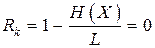
Таким образом, при кодировании сообщений с равновероятными буквами избыточность выбранного (равномерного) кода оказалась равной нулю.
Пусть теперь вероятности появления в тексте различных букв будут разными (табл. 7.2).
Вероятности появления букв
| А | Б | В | Г | Д | Е | Ж | З |
| Ра=0,6 | Рб=0,2 | Рв=0,1 | Рг=0,04 | Рд=0,025 | Ре=0,015 | Рж=0,01 | Рз=0,01 |
Энтропия источника 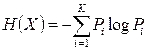
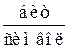
Среднее число символов на одно сообщение при использовании того же равномерного трехразрядного кода
Избыточность кода в этом случае будет
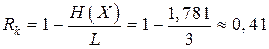
или довольно значительной величиной (в среднем 4 символа из 10 не несут никакой информации).
В связи с тем, что при кодировании неравновероятных сообщений равномерные коды обладают большой избыточностью, было предложено использовать неравномерные коды, длительность кодовых комбинаций которых была бы согласована с вероятностью выпадения различных букв.
Такое кодирование называется статистическим.
Операция кодирования тем более эффективна (экономична), чем меньшей длины кодовые слова сопоставляются сообщениям. Поэтому за характеристику эффективности кода примем среднюю длину кодового слова:

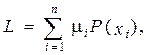

где 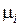

При установлении оптимальных границ для L исходят из следующих соображений. Во-первых, количество информации, несомое кодовым словом, не должно быть меньше количества информации, содержащегося в соответствующем сообщении, иначе при кодировании будут происходить потери в передаваемой информации. Во-вторых, кодирование будет тем более эффективным, чем большее количество информации будет содержать в себе каждый кодовый символ. Это количество информации максимально, когда все кодовые символы равновероятны, и равно 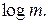

Шенноном сформулирована следующая теорема. При кодировании сообщений 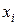
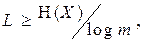
где H(X) – энтропия сообщения.
Если вероятности сообщений не являются целочисленными степенями числа m, точное достижение указанной границы невозможно, но при кодировании достаточно длинными группами к этой границе можно сколь угодно приблизиться.
Данная теорема не дает явных рецептов для нахождения кодовых слов со средней длиной (7.2), а поэтому она является теоремой существования. Важность этой теоремы состоит в том, что она определяет предельно возможную эффективность кода, позволяет оценить, насколько тот или иной конкретный код близок к самому экономному, и, наконец, придает прямой физический смысл одному из основных понятий теории информации – энтропии множества сообщений как минимальному числу двоичных символов (m = 2), приходящихся в среднем на одно сообщение.
Приведем два известных способа построения кодов, которые позволяют приблизиться к равновероятности и независимости кодовых символов.
Код Шеннона-Фано.
Для построения этого кода все сообщения Xi выписываются в порядке убывания их вероятностей (табл. 7.3).
Построение кода Шеннона-Фано
| xi | P(xi) | Разбиение сообщений на подгруппы | Код | mi | Lxi |
| x1 | 0,35 | 0,70 | |||
| x2 | 0,15 | 0,30 | |||
| x3 | 0,13 | 0,39 | |||
| x4 | 0,09 | 0,27 | |||
| x5 | 0,09 | 0,36 | |||
| x6 | 0,08 | 0,32 | |||
| x7 | 0,05 | 0,20 | |||
| x8 | 0,04 | 0,20 | |||
| x9 | 0,02 | 0,10 |
Записанные таким образом сообщения затем разбиваются на две по возможности равновероятностные подгруппы. Всем сообщениям первой подгруппы присваивают цифру 1 в качестве первого кодового символа, а сообщениям второй подгруппы – цифру 0. Аналогичное деление на подгруппы продолжается до тех пор, пока в каждую подгруппу не попадает по одному сообщению.
Найденный код весьма близок к оптимальному. В самом деле, энтропия сообщений:
|
Средняя длина кодового слова:
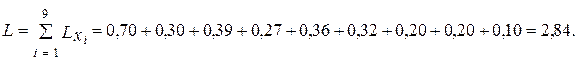
Среднее число нулей:
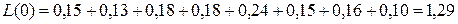
Среднее число единиц:
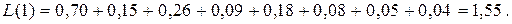
Вероятность появления нулей:
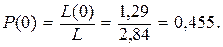
Вероятность появления единиц
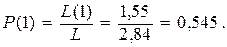
Таким образом, получили код близкий к оптимальному.
Код Хаффмана.
Для получения кода Хаффмана все сообщения выписывают в порядке убывания вероятностей. Две наименьшие вероятности объединяют скобкой (табл. 7.4) и одной из них присваивают символ 1, а другой – 0.
Затем эти вероятности складывают, результат записывают в промежутке между ближайшими вероятностями. Процесс объединения двух сообщений с наименьшими вероятностями продолжают до тех пор, пока суммарная вероятность двух оставшихся сообщений не станет равной единице. Код для каждого сообщения строится при записи двоичного числа справа налево путем обхода по линиям вверх направо, начиная с вероятности сообщения, для которого строится код.
Средняя длина кодового слова (табл. 7.4) L = 2,82, что несколько меньше, чем в коде Шеннона-Фано (L = 2,84). Кроме того, методика Шеннона-Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппы. От этого недостатка свободна методика Хаффмана. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву. Однако, как следует из приведенных выше цифр, некоторая избыточность в кодовых комбинациях осталась. Из теоремы Шеннона следует, что эту избыточность также можно устранить, если перейти к кодированию достаточно большими блоками.
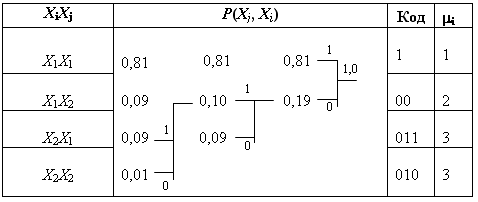
Построение кода Хаффмана




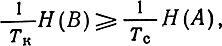
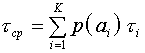
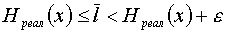

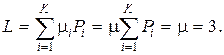
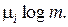
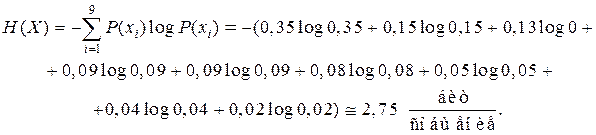






 0,02
0,02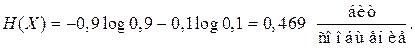 (7.8)
(7.8)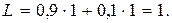 (7.9)
(7.9) (7.10)
(7.10)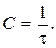 Избыточность кода равна избыточности источника сообщений:
Избыточность кода равна избыточности источника сообщений: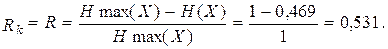
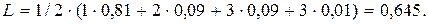 (7.11)
(7.11)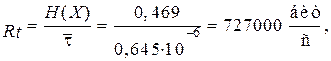 (7.12)
(7.12)
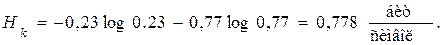



 X
X  X2X1X1
X2X1X1



 X2X1X2
X2X1X2
 X2X2X1
X2X2X1