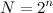цифровое кодирование это цифровое преобразование данных
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы “включено/выключено”. Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза “ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП”.
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Методы кодирования данных
Кодирование — это процесс преобразования данных или заданной последовательности символов, символов, алфавитов и т. Д. В определенный формат для защищенной передачи данных. Декодирование — это обратный процесс кодирования, который заключается в извлечении информации из преобразованного формата.
Кодировка данных
Кодирование — это процесс использования различных комбинаций уровней напряжения или тока для представления единиц и нулей цифровых сигналов в линии передачи.
Распространенными типами кодирования линий являются униполярный, полярный, биполярный и манчестерский.
Методы кодирования
Метод кодирования данных подразделяется на следующие типы в зависимости от типа преобразования данных.
Аналоговые данные для аналоговых сигналов. К этой категории относятся методы модуляции, такие как амплитудная модуляция, частотная модуляция и фазовая модуляция аналоговых сигналов.
Аналоговые данные для цифровых сигналов. Этот процесс можно назвать оцифровкой, которая осуществляется с помощью импульсной кодовой модуляции (PCM). Следовательно, это не что иное, как цифровая модуляция. Как мы уже обсуждали, выборка и квантование являются важными факторами в этом. Дельта-модуляция дает лучшую производительность, чем PCM.
Цифровые данные в цифровые сигналы — это в этом разделе. Есть несколько способов отобразить цифровые данные на цифровые сигналы. Некоторые из них —
Аналоговые данные для аналоговых сигналов. К этой категории относятся методы модуляции, такие как амплитудная модуляция, частотная модуляция и фазовая модуляция аналоговых сигналов.
Аналоговые данные для цифровых сигналов. Этот процесс можно назвать оцифровкой, которая осуществляется с помощью импульсной кодовой модуляции (PCM). Следовательно, это не что иное, как цифровая модуляция. Как мы уже обсуждали, выборка и квантование являются важными факторами в этом. Дельта-модуляция дает лучшую производительность, чем PCM.
Цифровые данные в цифровые сигналы — это в этом разделе. Есть несколько способов отобразить цифровые данные на цифровые сигналы. Некоторые из них —
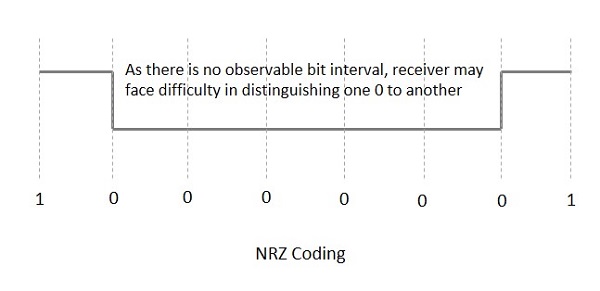
Невозврат в ноль (NRZ)
Коды NRZ имеют 1 для высокого уровня напряжения и 0 для низкого уровня напряжения. Основное поведение кодов NRZ состоит в том, что уровень напряжения остается постоянным в течение битового интервала. Конец или начало бита не будут указываться, и он будет поддерживать одно и то же состояние напряжения, если значение предыдущего бита и значение текущего бита совпадают.
На следующем рисунке поясняется концепция кодирования NRZ.
Если рассмотрен вышеприведенный пример, поскольку имеется длинная последовательность постоянного уровня напряжения, и тактовая синхронизация может быть потеряна из-за отсутствия битового интервала, приемнику становится трудно различать 0 и 1.
Аналого-цифровое преобразование для начинающих
В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП. Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.

В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.
Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением). Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.
Основные характеристики АЦП
АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно). Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.
Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:
Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.
Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.
Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.
Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.
АЦП прямого преобразования
АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.
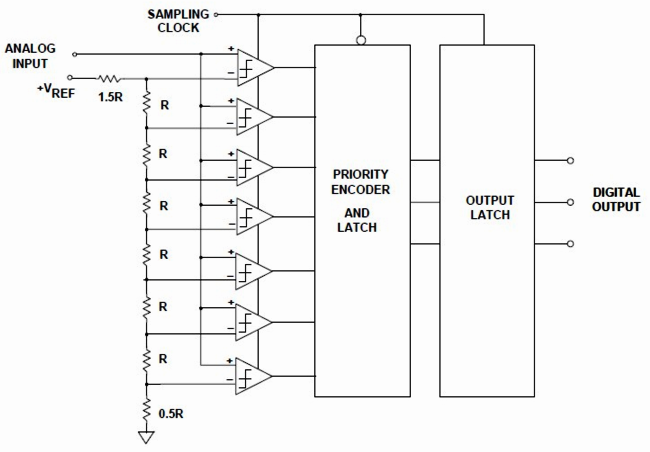
Архитектура АЦП прямого преобразования изображена на рис. 1
Рис. 1. Структурная схема АЦП прямого преобразования
Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.
Пусть на вход АЦП подается напряжение, равное 1/2 Uref. Тогда сработают первые 4 компаратора (если считать снизу), и на их выходах появятся логические единицы. Приоритетный шифратор (priority encoder) сформирует из «столбца» единиц двоичный код, который фиксируется выходным регистром.
Теперь становятся понятны достоинства и недостатки такого преобразователя. Все компараторы работают параллельно, время задержки схемы равно времени задержки в одном компараторе плюс время задержки в шифраторе. Компаратор и шифратор можно сделать очень быстрыми, в итоге вся схема имеет очень высокое быстродействие.
Но для получения N разрядов нужно 2^N компараторов (и сложность шифратора тоже растет как 2^N). Схема на рис. 1. содержит 8 компараторов и имеет 3 разряда, для получения 8 разрядов нужно уже 256 компараторов, для 10 разрядов – 1024 компаратора, для 24-битного АЦП их понадобилось бы свыше 16 млн. Однако таких высот техника еще не достигла.
АЦП последовательного приближения
АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.
Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:
1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).
2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).
3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.
Рис. 2. Структурная схема АЦП последовательного приближения.
Таким образом, АЦП последовательного приближения состоит из следующих узлов:
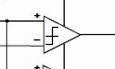
1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).
2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.
3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.
4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.
Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).
И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3.
Рис.3. Структурная схема сигма-дельта АЦП.
Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».
Рис. 4. Сигма-дельта АЦП как следящая система
Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].
На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).
Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.
Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.
Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.
Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):
Рис. 6. Структурная схема сигма-дельта модулятора
Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.
Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:
То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.
Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра
Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.
Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора. Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.
Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.
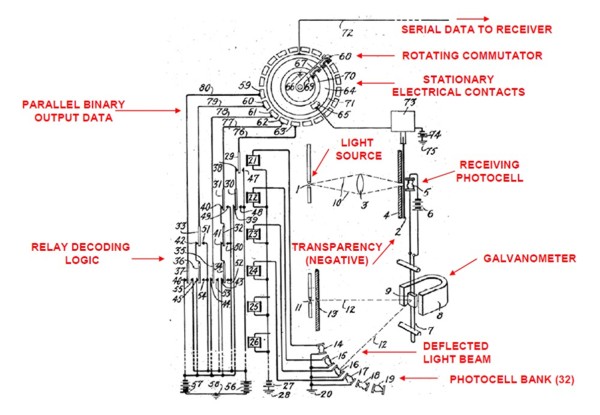
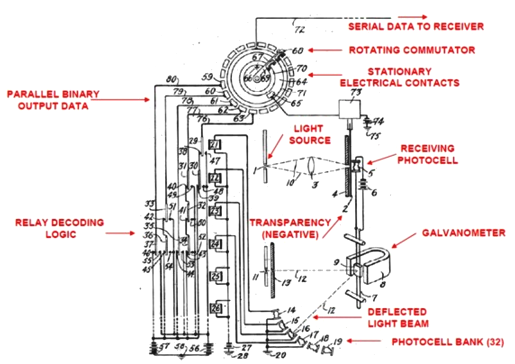
Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.
Рис. 8. Первый патент на АЦП
Рис. 9. АЦП прямого преобразования (1975 г.)
Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита. Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.
На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.
Рис. 10. АЦП прямого преобразования (1970 г.)
Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).
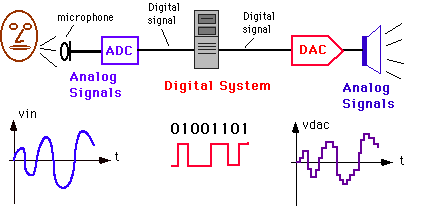
Как происходит преобразование аналогового сигнала в цифровой
В электронике сигналы делят на: аналоговые, дискретные и цифровые. Начнем с того, что все, что мы чувствуем, видим, слышим в большинстве своем является аналоговым сигналом, а то, что видит процессор компьютера – это цифровой сигнал. Звучит не совсем понятно, поэтому давайте разбираться с этими определениями и с тем как один вид сигналов преобразовывается в другой.
Содержание статьи
Типы сигналов
В электрическом представлении аналоговый сигнал, судя по его названию, является аналогом реальной величины. Например, вы чувствуете температуру окружающей среды постоянно, на протяжении всей жизни. Нет никаких перерывов. При этом вы чувствуете не только два уровня «горячо» и «холодно», а бесконечное число ощущений, которые описывают эту величину.
Отсюда следует, что у аналогового сигнала две особенности:
1. Непрерывность во времени.
2. Число величин сигнала стремится к бесконечности, т.е. аналоговый сигнал нельзя точно поделить на части или проградуировать, разбив шкалу на конкретные участки. Способы измерения – основаны на единице измерений, и их точность зависит лишь от цены деления шкалы, чем она меньше, тем точнее измерение.
Дискретные сигналы – это сигналы, которые представляют собой последовательность отчетов или измерений какой-либо величины. Измерения таких сигналов не непрерывны, а периодичны.
Попытаюсь объяснить. Если вы установили термометр где-нибудь он измеряет аналоговую величину – это следует из вышеописанного. Но вы, фактически следя за его показаниями, получаете дискретную информацию. Дискретный – значит отдельный.
Например, вы проснулись и узнали, сколько градусов на термометре, в следующий раз вы на него посмотрели на градусник в полдень, и третий раз вечером. Вы не знаете, с какой скоростью изменялась температура, равномерно, или резким скачком, вы знаете только данные в тот момент времени, который наблюдали.
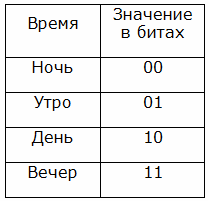
Цифровые сигналы – это набор уровней, типа 1 и 0, высокий и низкий, есть или нет. Глубина отражения информации в цифровом виде ограничена разрядностью цифрового устройства (набора логики, микроконтроллера, процессора etc.) Получается что для хранения булевых данных он подходит идеально. Пример, можно привести следующий, для хранений данных типа «День» и «Ночь», достаточно 1 бита информации.
Бит – это минимальная величина представления информации в цифровом виде, в нём может храниться только два типа значений 1 (логическая единица, высокий уровень), или 0 (логический ноль, низкий уровень).
В электронике бит информации представляется в виде низкого уровня напряжения (близкое к 0) и высокого уровня напряжения (зависит от конкретного устройства, часто совпадает с напряжением питания данного цифрового узла, типовые значения – 1.7, 3.3. 5В, 15В).
Все промежуточные значения между принятыми низким и высоким уровнем являются переходной областью и могут не обладать конкретным значением, в зависимости от схемотехники, как устройства в целом, так и внутренней схемы микроконтроллера (или любого другого цифрового устройства) могут иметь разный переходный уровень, например для 5-тивольтовой логики за ноль могут приниматься значения напряжения от 0 до 0.8В, а за единицу от 2В до 5В, при этом промежуток между 0.8 и 2В – это неопределенная зона, фактически с ее помощью отделяется ноль от единицы.
Чем более точные и ёмкие значения нужно хранить, тем больше нужно бит, приведем таблицу-пример с отображением в цифровом виде четырёх значений времени суток:
Ночь – Утро – День – Вечер
Для этого нам нужно уже 2 бита:
Аналогово-цифровое преобразование
В общем случае аналогово-цифровым преобразованием называется процесс перевода физической величины в цифровое значение. Цифровым значением является набор единиц и нолей воспринятых обрабатывающим устройством.
Такое преобразование нужно для взаимодействия цифровой техники с окружающей средой.
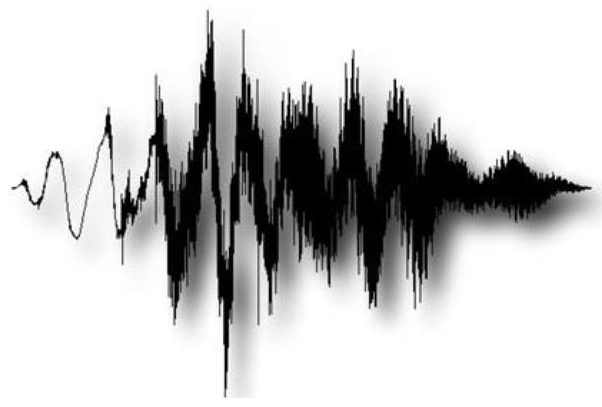
Так как аналоговый электрический сигнал повторяет своей формой входной сигнал, он не может быть записан в цифровом виде «так как есть» поскольку он имеет бесконечное число значений. Примером можно привести процесс записи звука. Он в первичном виде выглядит так:
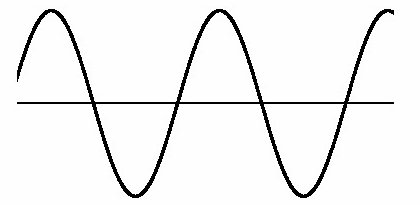
Он представляет собой сумму волн с различными частотами. Которые, при разложении по частотам (подробнее об этом смотрите преобразования Фурье), так или иначе, можно приблизить к похожей картинке:
Теперь попробуйте это представить в виде набора типа «111100101010100», довольно сложно, не так ли?
Другим примером необходимости преобразования аналоговой величины в цифровую, является её измерение: электронные термометры, вольтметры, амперметры и прочие измерительные приборы взаимодействую с аналоговыми величинами.
Как происходит преобразование?
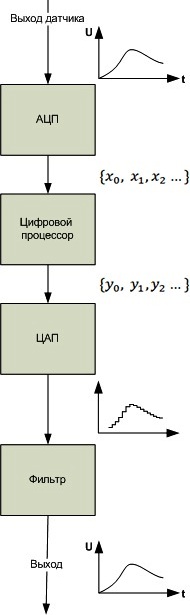
Сначала посмотрите на схему типового преобразования аналогового сигнала в цифровой и обратно. Позже мы к ней вернемся.
Фактически это сложный процесс, который состоит из двух основных этапов:
1. Дискретизация сигнала.
2. Квантование по уровню.
Дискретизация сигнала это определения промежутков времени, на которых измеряется сигнал. Чем короче эти промежутки – тем точнее измерение. Периодом дискретизации (Т) называется отрезок времени от начала считывания данных до его конца. Частота дискретизации (f) – это обратная величина:
После считывания сигнала происходит его обработка и сохранение в память.
Получается, что за время, которое считываются и обрабатываются показания сигнала, он может измениться, таким образом, происходит искажение измеряемой величины. Есть такая теорема Котельникова и из нее вытекает такое правило:
Частота дискретизации должны быть как минимум в 2 раза больше чем частота дискретизируемого сигнала.
Это скриншот из википедии, с выдержкой из теоремы.
Для определения численного значение необходимо квантование по уровню. Квант – это определенный промежуток измеряемых значений, усреднено приведенный к определенному числу.
Т.е. сигналы величиной от X1 до X2, условно приравнивается к определенному значению Xy. Это напоминает цену деления стрелочного измерительного прибора. Когда вы снимаете показания, зачастую вы их равняете по ближайшей отметке на шкале прибора.
Так и с квантованием по уровню, чем больше квантов, тем более точные измерения и тем больше знаков после запятой (сотых, тысячных и так далее значений) они могут содержать.
Точнее сказать число знаков после запятой скорее определяется разрядностью АЦП.
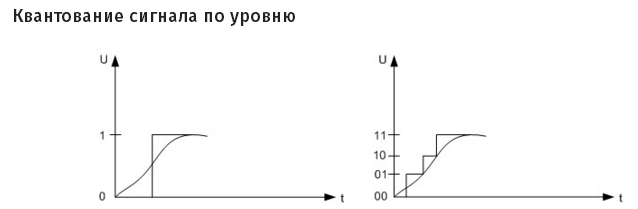
На картинке изображен процесс квантования сигнала с помощью одного бита информации, как я описывал выше, когда при превышении определенного предела принимается значение высокого уровня.
Справа показано квантование сигнала, и запись в виде двух бит данных. Как видите, этот фрагмент сигнала разбит уже на четыре значения. Получается, что в результате плавный аналоговый сигнал превратился в цифровой «ступенчатый» сигнал.
Количество уровней квантования определяется по формуле:
Где n — количество разрядов, N — уровень квантования.
Вот пример сигнала разбитого на большее число квантов:
Отсюда очень хорошо видно, что чем чаще снимаются значения сигнала (больше частота дискретизации), тем точнее он измеряется.
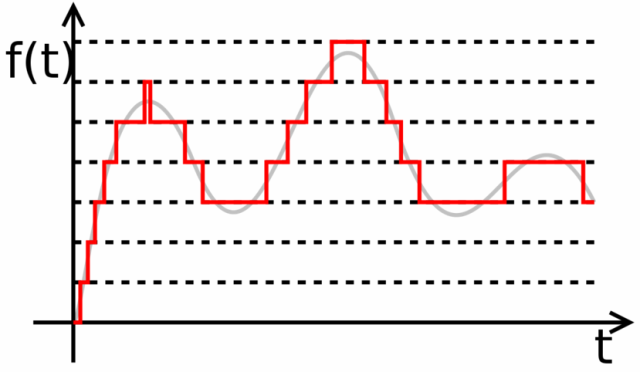
На этой картинке изображено преобразование аналогового сигнала в цифровой вид, а слева от оси ординат (вертикальной оси) запись в цифровом 8-битном виде.
Аналогово-цифровые преобразователи
АЦП или Аналогово-цифровой преобразователь может выполняться в виде отдельного устройства или быть встроенным в микроконтроллер.
Ранее в микроконтроллеры, например семейства MCS-51, не содержали в своем составе АЦП, использовалась для этого внешняя микросхема и возникала необходимость писать подпрограмму обработки значений внешней ИМС.
Сейчас они есть в большинстве современных микроконтроллеров, например AVR AtMEGA328, который является основой большинства популярных плат Ардуино, он встроен в сам МК. На языке Arduino чтение аналоговых данных осуществляется просто – командой AnalogRead(). Хотя в микропроцессоре, который установлен в той же не менее популярной Raspberry PI его нет, так что не все так однозначно.
Фактически существует большое число вариантов аналогово-цифровых преобразователей, у каждого из которых есть свои недостатки и преимущества. Описывать которые в пределах этой статьи не имеет особого смысла, так как это большой объём материала. Рассмотрим лишь общую структуру некоторых из них.
Самым старым запатентованным вариантом АЦП, является патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Это 5-ти битный АЦП прямого преобразования. Из названия патента приходят мысли о том, что использование этого прибора было связано с передачей данных через телеграф.
Если говорить о современных АЦП прямого преобразования имеют следующую схему:
Отсюда видно, что вход представляет собой цепочку из компараторов, которые на выходе своем выдают сигнал при пересечении какого-то порогового сигнала. Это и есть разрядность и квантование. Кто хоть немного силен в схемотехнике, увидел этот очевидный факт.
Кто не силен, то входная цепь работает таким образом:
Аналоговый сигнал поступает на вход «+», на все сразу. На выходы с обозначением «-» поступает опорное напряжение, которое раскладывается с помощью цепочки резисторов (резистивного делителя) на ряд опорных напряжений. К примеру, ряд для этой цепи выглядит наподобие такого соотношения:
Urefi=(1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16)*Uref
В скобках через запятую указано, какую часть от общего опорного напряжения Uref подают на вход каждого входного напряжения.
Т.е. каждый из элементов имеет два входа, когда напряжение на входе со знаком «+» превышает напряжение на входе со знаком «-», то на его выходе появляется логическая единица. Когда на положительном (неинвертирующем) входе напряжение меньше, чем на отрицательно (инвертирующем), то на выходе – ноль.
Напряжение делиться таким образом, чтобы входное напряжение разбить на нужное количество разрядов. При достижении напряжения на входе на выходе соответствующего элемента появляется сигнал, схема обработки выводит «правильный» сигнал в цифровом виде.
Такой компаратор хорош скоростью обработки данных, все элементы входной цепи срабатывают параллельно, основная задержка этого вида АЦП формируется из задержки 1 компаратора (все же одновременно параллельно срабатывают) и задержки шифратор.
Однако есть огромный недостаток параллельных цепей – это необходимость большого числа компараторов, для получения АЦП высокой разрядности. Чтобы получить, например 8 разрядов, нужно 2^8 компараторов, а это целых 256 штук. Для десятиразрядного (в ардуино 10-разрядный АЦП, кстати, но другого типа) нужно 1024 компаратора. Судите сами о целесообразности такого варианта обработки, и где он может понадобиться.
Есть и другие виды АЦП:
Преобразование аналогового сигнала в цифровой нужно для считывания параметров с аналоговых датчиков. Есть отдельный вид цифровых датчиков, они представляют собой либо интегральные микросхемы, например DS18b20 – на его выходе уже цифровой сигнал и его можно обрабатывать любыми микроконтроллерами или микропроцессорами без необходимости применения АЦП, или аналоговый датчик на плате на которой уже размещен свой преобразователь. У каждого типа датчиков есть свои плюсы и минусы, такие как помехоустойчивость и погрешность измерений.
Знание принципов преобразование обязательно для всех кто работает с микроконтроллерами, ведь не в каждой даже современной системе встроены такие преобразователи, приходится использовать внешние микросхемы. Для примера можно привести такую плату, разработанную специально под GPIO-разъём Raspberry PI, с прецизионным АЦП на ADS1256.
Обучение программированию и созданию устройств на микроконтроллерах AVR
Цель состоит в том, чтобы, не углубляясь в подробности, освоить технологию программирования и быстро получить конкретный результат. Полное представление, навыки и умения появятся позже в процессе работы.
Освоить работу с микроконтроллерами в режиме “быстрый старт”, научиться их программировать и создавать различные полезные умные электронные устройства можно легко с помощью обучающих видеокурсов Максима Селиванова в которых все основные моменты разложены по полочкам.
Методика быстрого изучения принципов работы с микроконтроллерами основывается на том, что достаточно освоить базовую микросхему, чтобы затем достаточно уверенно составлять программы к другим ее разновидностям. Благодаря этому первые опыты по программировании микроконтроллеров проходят без особых затруднений. Получив базовае знания можно приступать к разработке собственных конструкций.
На данный момент у Максима Селиванова есть 4 курса по созданию устройств на микроконтроллерах, построенные по принципу от простого к сложному.
Курс для тех, кто уже знаком с основами электроники и программирования, кто знает базовые электронные компоненты, собирает простые схемы, умеет держать паяльник и желает перейти на качественно новый уровень, но постоянно откладывает этот переход из-за сложностей в освоении нового материала.
Курс замечательно подойдет и тем, кто только недавно предпринял первые попытки изучить программирование микроконтроллеров, но уже готов все бросить от того, что у него ничего не работает или работает, но не так как ему нужно (знакомо?!).
Курс будет полезен и тем, кто уже собирает простенькие (а может и не очень) схемы на микроконтроллерах, но плохо понимает суть того как микроконтроллер работает и как взаимодействует с внешними устройствами.
Курс рассчитан на подготовленного слушателя. То есть, в курсе не рассматриваются базовые основы информатики и электроники и микроконтроллеров. Но, что бы освоить курс понадобятся минимальные знания по программированию микроконтроллеров AVR на любом языке. Знания электроники желательны, но не обязательны.
Курс идеально подойдет тем, кто только начал изучать программирование AVR микроконтроллеров на языке С и хочет углубить свои знания. Хорошо подойдет и тем, кто немного умеет программировать микроконтроллеры на других языках. И еще подойдет обычным программистам, которые хотят углубить знания в языке Си.
Этот курс для тех, кто не хочет ограничиваться в своем развитии простыми или готовыми примерами. Курс отлично подойдет тем, кому важно создание интересных устройств с полным пониманием того, как они работают. Курс хорошо подойдет и тем, кто уже знаком с программированием микроконтроллеров на языке Си и тем, кто уже давно программирует их.
Материал курса прежде всего ориентирован на практику использования. Рассматриваются следующие темы: радиочастотная идентификация, воспроизведение звука, беспроводной обмен данными, работа с цветными TFT дисплеями, сенсорным экраном, работа с файловой системой FAT SD-карты.
Дисплеи NEXTION представляют собой программируемые дисплеи с тачскрином и UART для создания самых разных интерфейсов на экране. Для программирования используется очень удобная и простая среда разработки, которая позволяет создавать даже очень сложные интерфейсы для различной электроники буквально за пару вечеров! А все команды передаются через интерфейс UART на микроконтроллер или компьютер. Материал курса составлен по принципу от простого к сложному.
Приближается осень, а вместе с ней наступит День знаний! Это отличная пора для новых дел, идей и начинаний и самое время для обучения. Используйте это время с пользой для прокачки своих знаний!
Полный курс обучения программированию микроконтроллеров со скидкой: Все 4 курса со скидкой
Любите умные гаджеты и DIY? Станьте специалистом в сфере Internet of Things и создайте сеть умных гаджетов!
Записывайтесь в онлайн-университет от GeekBrains:
Изучить C, механизмы отладки и программирования микроконтроллеров;
Получить опыт работы с реальными проектами, в команде и самостоятельно;
Получить удостоверение и сертификат, подтверждающие полученные знания.
Starter box для первых экспериментов в подарок!
После прохождения курса в вашем портфолио будет: метостанция с функцией часов и встроенной игрой, распределенная сеть устройств, устройства регулирования температуры (ПИД-регулятор), устройство контроля влажности воздуха, система умного полива растений, устройство контроля протечки воды.
Вы получите диплом о профессиональной переподготовке и электронный сертификат, которые можно добавить в портфолио и показать работодателю.