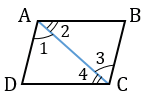
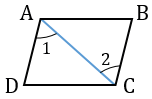
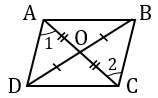
диагонали пересекаются и точкой пересечения делятся пополам у каких фигур

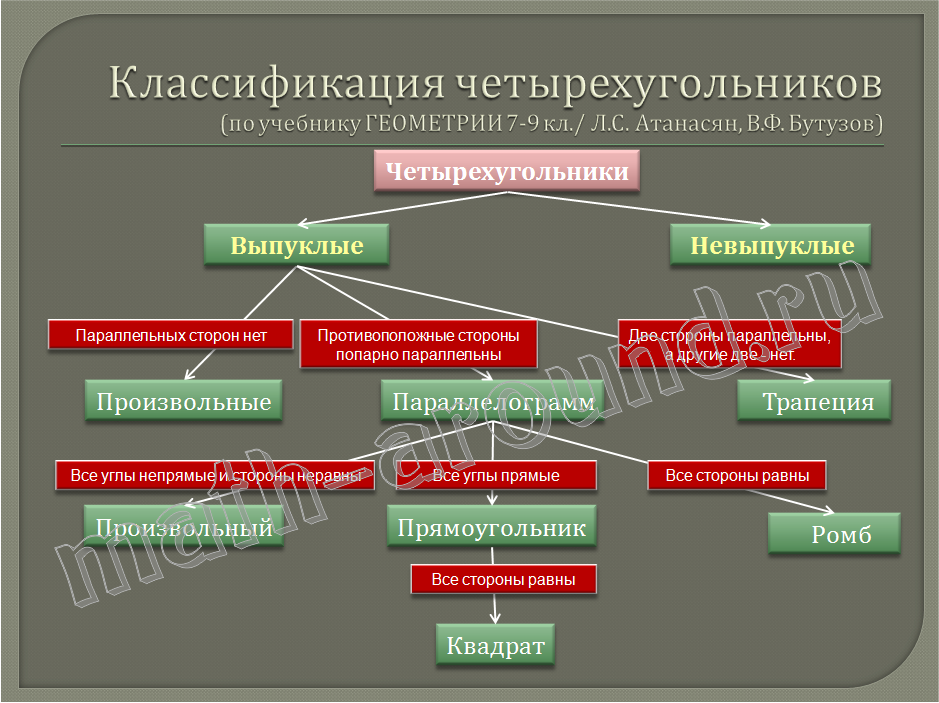
Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

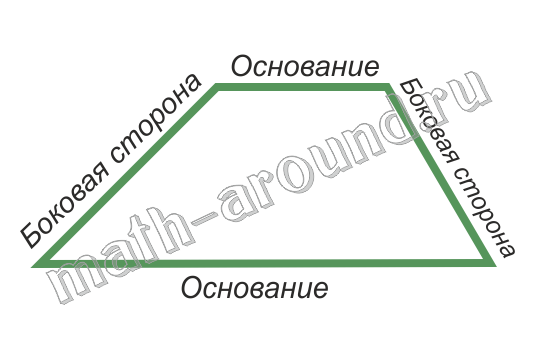
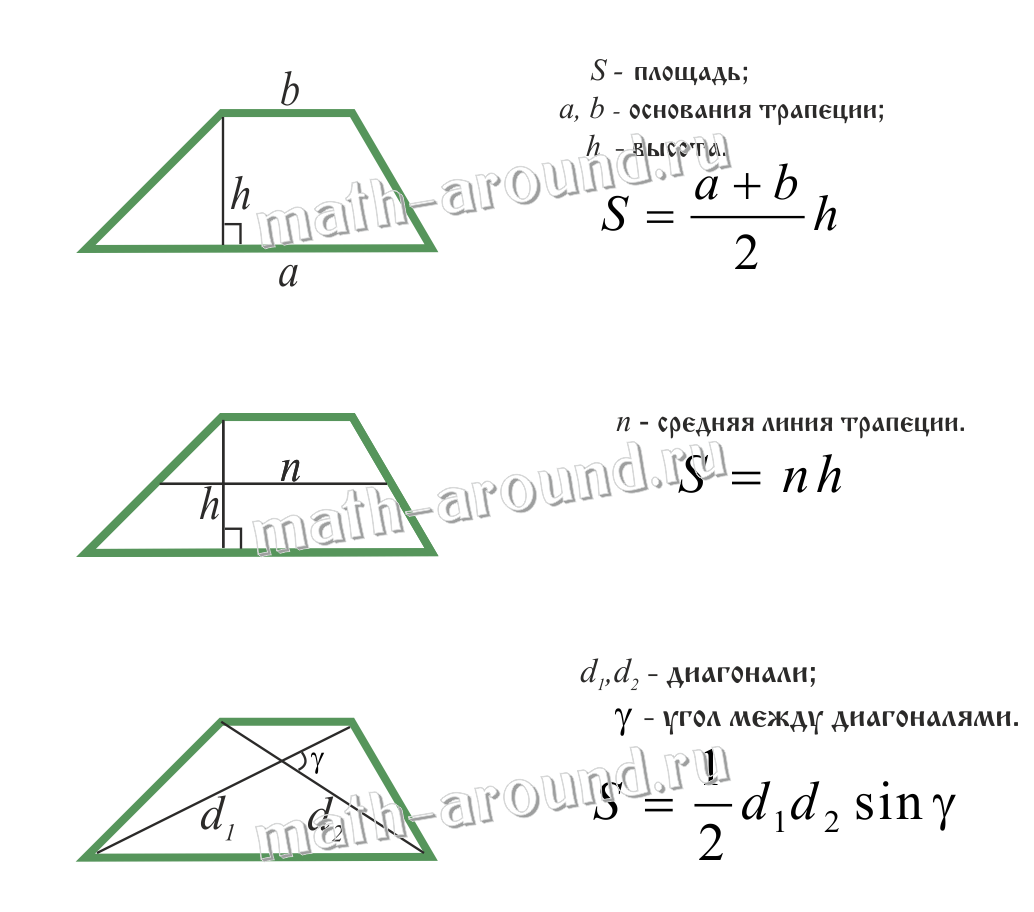
Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

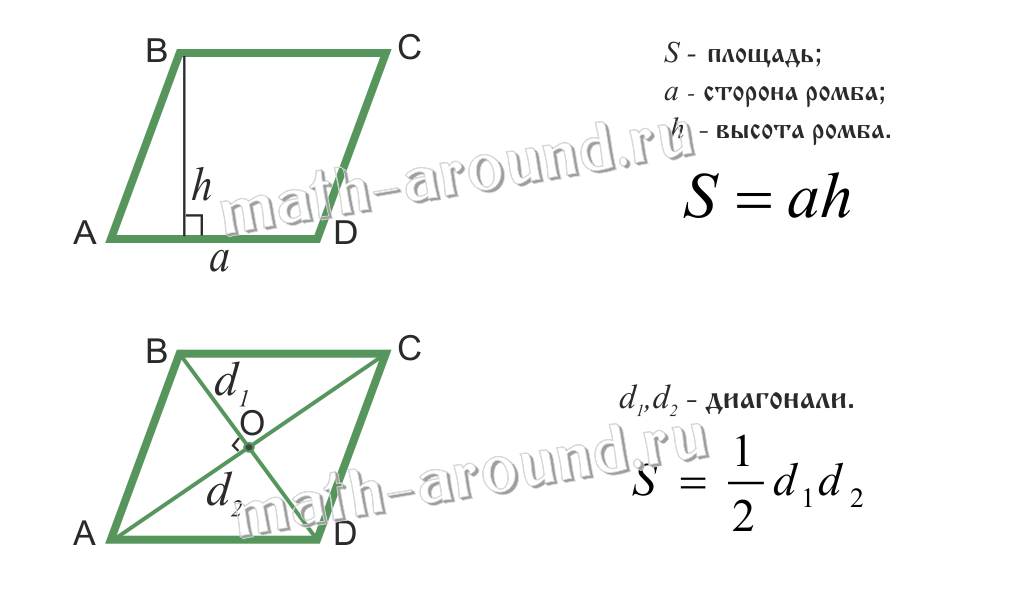
Ромб — это параллелограмм с равными сторонами.

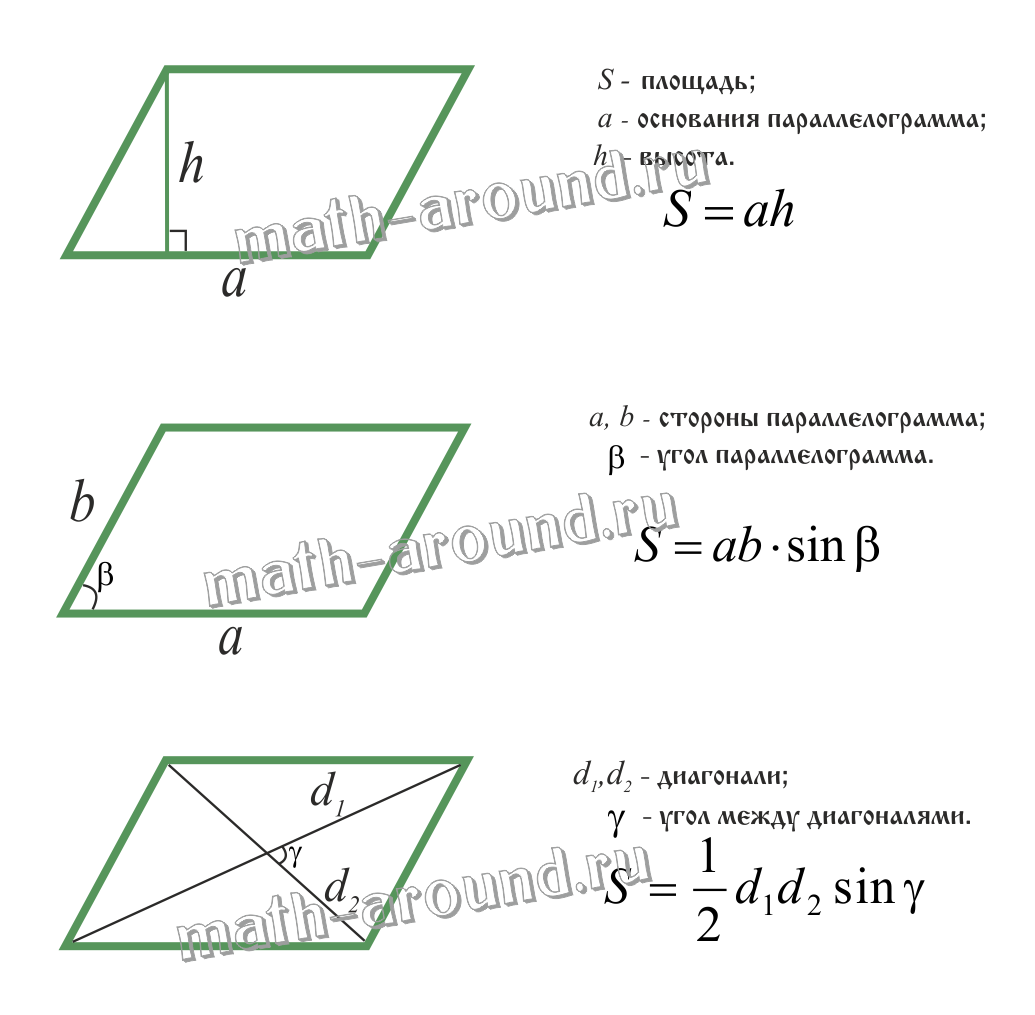
Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Диагонали пересекаются и точкой пересечения делятся пополам у каких фигур

Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.

Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.

Трапеция

Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.

Трапеция называется равнобедренной (равнобочной), если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

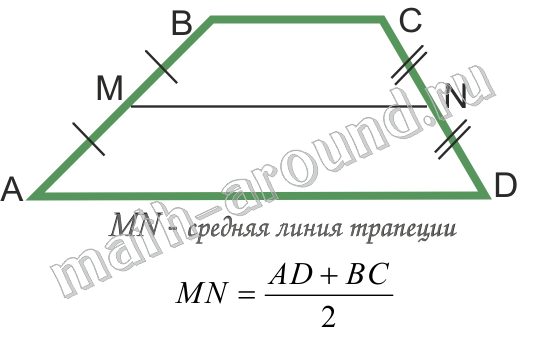
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Средняя линия параллельна основаниям и равна их полусумме.

Прямоугольник

Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойство. Диагонали прямоугольника равны.

Определение. Ромбом называется параллелограмм, у которого все стороны равны.

Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадрат

Определение. Квадратом называется прямоугольник, у которого все стороны равны.

Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.

Свойства:
1. Все углы квадрата прямые

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Источник

Признаки параллелограмма

Доказательство:

Дано: АВСD — четырехугольник, АD = ВС, АDВС.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

Доказательство:

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Доказать: АВСD — параллелограмм.

Доказательство:

1. Рассмотрим АОD и ВОС: по условию АО = ОС, DО = ОВ, АОD и ВОС (как вертикальные углы), АОD =ВОС (по 1 признаку равенства треугольников), АD = ВC и 1 = 2.

2. 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом 1 = 2, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Источник

Параллелограмм — признаки и свойства

Клод Бернард однажды сказал:

«Думать, что всё знаешь, останавливает тебя от того, чтобы учиться новому»

Давай узнаем что-то новое сегодня, разбирая, казалось бы, такую простую тему!

Статья поможет тебе окончательно разобраться с самыми «популярными» параллелограммами, а наши вебинары дадут тебе необходимую практику.

И на ЕГЭ ты сможешь решить любую задачу на эту тему!

Параллелограмм — коротко о главном

Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма:

Прямоугольник – четырехугольник, все углы которого прямые: \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).

Свойства прямоугольника:

Ромб – четырехугольник, все стороны которого равны между собой: \( \displaystyle AB=BC=CD=DA\).

Свойства ромба:

Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые: \( \displaystyle AB=BC=CD=DA\); \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).

Свойства квадрата:

\( \displaystyle ABCD\) – ромб

Источник

Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.

Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.

На рисунках изображены четырехугольники.

Рассмотрим основные виды четырехугольников, их свойства, формулы площади:

Параллелограмм

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

ABCD-параллелограмм: AB||DC, AD||BC

Свойства:

Признаки параллелограмма:

Площадь параллелограмма:

Трапеция

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

ТЕОРЕМА.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Площадь трапеции:

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства:

Площадь ромба:

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы равны.

Свойства:

Признак прямоугольника:

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Площадь прямоугольника:

Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства:

Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).

Площадь квадрата:

Автор: Аникина Марина

Комментарии к этой заметке:

Очень понравилась эта статья ) Все интересно и понятно) Очень помогло! Спасибо)

Очень понятный и краткий текст). Все очень понравилось!

Источник