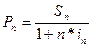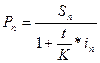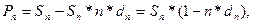дисконтирующий множитель показывает какую долю составляет первоначальная величина долга в его сумме

Математическое дисконтирование

Напомним, что n=t/К — срок ссуды в годах.

Установленная таким путем величина Р является современной величиной суммы S, которая будет выплачена спустя n лет. Дробь 1/(1 + ni) называют дисконтным или дисконтирующим множителем. Этот множитель показывает, какую долю составляет первоначальная величина долга в окончательной его сумме. В математике финансов дисконтом является величина, вычитаемая из суммы погашения обязательства, когда обязательство принимается до даты его погашения. Сумма, остающаяся после вычитания дисконта из суммы погашения, называется выручкой.Например, предположим, что Иванов получил вексель от Петрова на 10000 руб., которые будут погашены через 5 месяцев. После этого Иванов продает этот вексель Сидорову за 9500. В этом случае дисконт равен 500 руб. и выручка равна 9500 руб.

Пример 9. Через 180 дней после подписания договора должник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням? Согласно (10) находим

P=310/(1+(180/365)0,16)=287,32859 тыс. руб.

Разность S — Р можно рассматривать не только как проценты, начисленные на Р, но и как дисконт с суммы S.

Банковский учет (учет векселей).Суть операции заключается в следующем. Банк или другое финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает у его владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк получает доход в виде дисконта. В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги хотя и не в полном объеме, но ранее указанного на нем срока.

При учете векселя применяется банковский или коммерческий учет.

Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d. Размер дисконта, или суммы учета равен Snd; если d — годовая учетная ставка, то n измеряется в годах. Таким образом,

P = S – Snd = S (1 – nd), (1.11)

где n — срок от момента учета до даты погашения векселя.

Учет посредством учетной ставки чаще всего осуществляется при временной базе К= 360 дней, число дней ссуды обычно берется точным.

Пример 10. Тратта (переводной вексель) выдан на сумму 1 млн. руб. с уплатой 17.11.2009г. Владелец векселя учел его в банке 23.09.2008 по учетной ставке 20%. Оставшийся до конца срока период равен 55 дням. Полученная при учете сумма (без уплаты комиссионных) равна P = 1 000 000 (1-(55/360)0,2)=969444,4 руб.

Дисконт составит 30 555,6 руб.

Наращение по учетной ставке.Простая учетная ставка иногда применяется и при расчете наращенной суммы. В частности, в этом возникает необходимость при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга. Наращенная сумма в этом случае

Пример 11. По данным примера 2 определим наращенную сумму при условии, что проценты начисляются по простой учетной ставке d = 18%:

S=1 000 000(1/(1-(258/360)0,18)=1 148 105,62 руб.

Источник

Дисконтирование и учет по простым процентным ставкам. Рост по учетной ставке

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды Р. Такая ситуация может возникнуть, например, при разработке условий контракта. Расчет Р по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этих случаях говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты — дисконтом (discount). Необходимость дисконтирования возникает, например, при покупке краткосрочных обязательств, оплата которых должником произойдет в будущем.

Термин «дисконтирование» употребляется и в более широком смысле — как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому, обычно начальному, моменту времени. (Строго говоря, приведение может быть осуществлено на любой момент времени.)

Величину Р,найденную с помощью дисконтирования, называют современной величиной (present value) суммы S, a иногда, в зависимости от контекста, — современной (текущей, капитализированной) стоимостью. Современная величина суммы денег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения учитывается такой фактор, как время. Как будет показано далее, большинство аналитических методов основывается на определении современной величины платежей.

В зависимости от вида процентной ставки применяют два метода дисконтирования — математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором — учетная ставка.

Математическое дисконтирование.Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды. Задача в этом случае формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i? Решив уравнение (1.1) относительно Р, находим:

. (1.7)

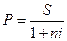
Напомним, что п = t/K — срок ссуды в годах. Установленная таким путем величина Р является современной величиной суммы S, которая будет выплачена спустя п лет. Дробь 1/(1 + ni) называют дисконтным множителем. Этот множитель показывает, какую долю составляет первоначальная величина долга в окончательной его сумме.

Пример 1.8.Через 180 дней после подписания договора должник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?

Согласно формуле (1.7) находим:

руб.

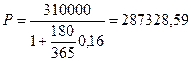
Разумеется, дисконт как скидка с конечной суммы долга необязательно определяется через процентную ставку, он может быть установлен по соглашению сторон и в виде абсолютной величины для всего срока.

Банковский учет (учет векселей).Суть операции заключается в следующем. Банк или иное финансовое учреждение до наступления срока платежа (date of maturity) по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги, хотя и не в полном объеме, однако раньше указанного на нем срока. При учете векселя применяется банковский, или коммерческий, учет (bank discount). Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока (maturity value). При этом применяется учетная ставка d.

Размер дисконта, или суммы учета, очевидно, равен Snd;если d — годовая ставка, то п измеряется в годах. Таким образом:

где п — срок от момента учета до даты погашения векселя.

Учет посредством учетной ставки чаще всего осуществляется при временной базе K = 360 дней, число дней ссуды обычно берется точным.

Пример 1.9.Тратта (переводной вексель) выдан на сумму 1 млн. руб. с уплатой 17 ноября 1995 г. Владелец векселя учел его в банке 23 сентября 1995 г. по учетной ставке 20%. Оставшийся до конца срока период равен 55 дням. Полученная при учете сумма (без уплаты комиссионных) равна

руб.

Дисконт составит 30 555,6 руб.

Продолжим пример. Пусть на первоначальную сумму долга (1 млн. руб.) начисляются проценты по ставке простых процентов i = 20,5% годовых. В этом случае, очевидно, надо решить две задачи: определить наращенную сумму долга и сумму, получаемую при учете. Оба последовательных действия можно представить в одной формуле:

где п — общий срок обязательства,

n’ — срок от момента учета до погашения.

Пусть в данном примере п = 120/360, тогда

руб.

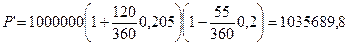
Наращение по учетной ставке.Простая учетная ставка иногда применяется и при расчете наращенной суммы. В частности, в этом возникает необходимость при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга. Наращенная сумма в этом случае

(1.9)

Множитель наращения здесь равен 1/(1 — nd).Заметим, что при п > 1/d расчет лишен смысла, так как наращенная сумма становится бесконечно большим числом.

Пример 1.10.По данным примера 1.2 определим наращенную сумму при условии, что проценты начисляются по простой учетной ставке d = 18%.

руб.

Источник

Дисконтирование и учет по простым процентным ставкам

Тема 3. Современная стоимость денежных средств (дисконтирование)

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной наращенной сумме S, которую следует упла­тить через некоторое время n, необходимо определить сумму полу­ченной ссуды Р.Такая ситуация может возникнуть, например, при разработке условии контракта. Расчет Р по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредст­венно при выдаче ссуды. В этих случаях говорят, что сумма Sдисконтируетсяили учитывается,сам процесс начисления процен­тов и их удержание называют учетом,а удержанные проценты – дисконтом. Необходимость дисконтирования возникает, например, при покупке краткосрочных обязательств, оплата кото­рых должником произойдет в будущем.

Дисконт (от англ. discount (D) – разница между ценой в настоящий момент и ценой на момент погашения или ценой номинала ценной бумаги.

Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Такой прием часто называют приведениемстоимостного показателя к некоторому, обычно начальному, моменту времени (приведение может быть осуществлено на любой момент времени.)

Дисконтирование – приведение стоимостных показателей к одному моменту времени.

Величину Р, найденную с помощью дисконтирования, называют современной величиной суммы S, а иногда, в зависи­мости от контекста, – современной (текущей, приведенной) стоимостью.Современная величина суммы денежных средств является одним из важнейших понятий в количественном анализе финансовых опе­раций. В большинстве случаев именно с помощью дисконтирова­ния, а не наращения учитывается такой фактор, как время. Как бу­дет показано далее, большинство аналитических методов основыва­ется на определении современной величины платежей.

Следует иметь в виду, что привести стоимость денег можно к любому нужному моменту времени, а не обязательно к началу финансовой операции. Кроме того, с помощью дисконтирования определяют современную стоимость денег независимо от того, действительно ли совершалась кредитная операция и можно ли считать дисконтируемую сумму буквально наращенной.

В зависимости от вида процентной ставки применяют два мето­да дисконтирования:

ü математическое дисконтирование–используется ставка на­ращения;

ü банков­ский (коммерческий) учет– используется учетная ставка.

Математическое дисконтирование.Математическое дисконтирова­ние представляет собой формальное решение задачи, обратной на­ращению первоначальной суммы ссуды. Задача в этом случае фор­мулируется так: какую первоначальную сумму денежных средств надо выдать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i? Решив уравнение от­носительно Р,находим:

Напомним, что n = t/K – срок ссуды в годах. Установленная та­ким путем величина Рявляется современной величиной суммы S,которая будет выплачена спустя nлет.

Дробь 1/(1 + n*i)называют дисконтным множителем. Этот множитель показывает, какую долю составляет первоначальная величина долга в окончательной его сумме.

Пример 18. Через 180 дней после подписания кредитного договора Соколов А.А. уплатит 310000 рублей. Кредит выдан под 16% годовых. Какова первоначальная сумма долга и величина дисконта при условии, что временная база равна 365 дням?

Решение:

руб.

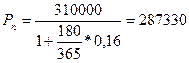
Дисконт равен 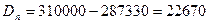руб.

Разумеется, дисконт как скидка с конечной суммы долга необя­зательно определяется через процентную ставку, он может быть установлен по соглашению сторон и в виде абсолютной величины для всего срока.

Банковский (коммерческий) учет (учет векселей).Суть операции заключается в сле­дующем. Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежно­му обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (со скидкой). Получив при наступлении сро­ка векселя деньги, банк реализует дисконт. В свою очередь владе­лец векселя с помощью его учета имеет возможность получить денежные средства, хотя и не в полном объеме, однако раньше указанного на нем срока. При учете векселя применяется банковский (ком­мерческий)учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом при­меняется учетная ставка d.

Размер дисконта (D), или суммы учета равен S*n*d,если d– годовая ставка, то nизмеряется в годах. Таким образом:

где n – срок от момента учета до даты погашения векселя;

d_п – дисконтная ставка.

Дисконтный множитель здесь равен (1 – n*d).

Учет посредством учетной ставки чаще всего осуществляется при временной базе К= 360 дней, число дней ссуды обычно берется точным.

Пример 19.Тратта (переводной вексель) выдан на сумму 1 млн. рублей с уплатой 17 ноября 2005 года. Владелец векселя учел его в бан­ке 23 сентября 2005 года по учетной ставке 20%. Оставшийся до конца срока период равен 55 дням. Сколько составит полученная при учете сум­ма (без уплаты комиссионных)?

Решение:

руб.

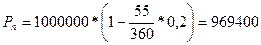
Дисконт составит 30600 руб.

Как было показано выше, оба вида ставок применяются для ре­шения сходных задач. Однако для ставки наращения прямой зада­чей является определение наращенной суммы, обратной – дискон­тирование. Для учетной ставки, наоборот, прямая задача заключа­ется в дисконтировании, обратная – в наращении.

Очевидно, что рассмотренные два метода дисконтирования – по ставке наращения i и учетной ставке d – приводят к разным резуль­татам даже тогда, когда i = d.

Заметим, что учетная ставка отражает фактор времени более же­стко. Так, из формулы следует, что при n > 1/d величина дис­контного множителя и, следовательно, суммы Р станет отрицатель­ной. Иначе говоря, при относительно большом сроке векселя учет может привести к нулевой или даже отрицательной сумме Р, что лишено смысла. Например, при d = 20% уже пятилетний срок дос­таточен для того, чтобы владелец векселя ничего не получил при его учете.

Влияние фактора времени усиливается при увеличении величи­ны ставки. Так, при d = 100% отрицательный результат проявится уже при n > 1. Такая ситуация не возникает при математическом дисконтировании: при любом сроке современная величина платежа здесь больше нуля.

Источник

Банковский учет

Математическое дисконтирование

Математическое дисконтирование – определение первоначальной суммы долга, которая при начислении процентов по заданной величине процентной ставки ( i ) позволит к концу срока получить указанную наращенную сумму:

для простых процентов

где k_д – дисконтный множитель (коэффициент приведения) для простых процентов.

Дисконтный множитель показывает, какую долю составляет первоначальная сумма долга в величине наращенной суммы. Поскольку дисконтный множитель (множитель приведения) зависит от двух аргументов (процентной ставки и срока ссуды), то его значения легко табулируются, что облегчает финансовые расчеты.

Пример. Через 150 дней с момента подписания контракта необходимо уплатить 310 тыс. руб., исходя из 8% годовых и временной базы 360 дней. Определить первоначальную сумму долга.

Решение:

Поскольку срок ссуды менее года, то используем формулу простых процентов:

= 310’000 • 1 / (1 + 150 / 360 • 0,08) = 300’000 руб.

PV = FV • k_д = 310’000 • 0,9677419 = 300’000 руб.

Таким образом, первоначальная сумма долга составила 300 тыс. руб., а проценты за 150 дней – 10 тыс. руб.

Для сложных процентов

где k_д – дисконтный множитель для сложных процентов.

Если начисление процентов производится m раз в год, то формула примет вид:

Пример. Через два года фирме потребуется деньги в размере 30 млн руб., какую сумму необходимо сегодня поместить в банк, начисляющий 25% годовых, чтобы через 2 года получить требуемую сумму?

Решение:

Поскольку срок финансовой операции составляет более года, что используем формулу приведения для сложных процентов:

= 30’000’000 • 1 / (1 + 0,25) 2 = 19’200’000 руб.

PV = FV • k_д = 30’000’000 • 0,6400000 = 19’200’000 руб.

Таким образом, фирме следует разместить на счете 19’200’000 руб. под 25% годовых, чтобы через два года получить желаемые 30’000’000 руб.

Современная величина и процентная ставка, по которой проводится дисконтирование, находятся в обратной зависимости: чем выше процентная ставка, тем при прочих равных условиях меньше современная величина.

В той же обратной зависимости находятся современная величина и срок финансовой операции: чем выше срок финансовой операции, тем меньше при прочих равных условиях современная величина.

Банковский учет – второй вид дисконтирования, при котором исходя из известной суммы в будущем, определяют сумму в данный момент времени, удерживая дисконт.

Операция учета (учет векселей) заключается в том, что банк или другое финансовое учреждение до наступления платежа по векселю покупает его у предъявителя по цене ниже суммы векселя, т.е. приобретает его с дисконтом. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока его погашения. Подобным образом (с дисконтом) государство продает большинство своих ценных бумаг.

Для расчета дисконта используется учетная ставка:

где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем.

Очевидно, что чем выше значение учетной ставки, тем больше дисконт. Дисконтирование по простой учетной ставке чаще всего производится по французской практике начисления процентов, т.е. когда временная база принимается за 360 дней, а число дней в периоде берется точным.

Пример. Вексель выдан на 5’000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта.

Решение:

Для определения суммы при учете векселя рассчитываем число дней, оставшихся до погашения обязательств:

Отсюда, определяемая сумма:

Тогда дисконт составит:

D = FV • t / T • d = 5’000 • 90 / 360 • 0,08 = 100 руб.

Следовательно, предъявитель векселя получит сумму 4’900 руб., а банк при наступлении срока векселя реализует дисконт в размере 100 руб.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т.к. учетная ставка каждый раз применяется к уменьшаемой на величину дисконта величине.

Пример. Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть ее через два года в размере 55 тыс. руб. Банк определяет свой доход с использованием годовой учетной ставки 30%.

Решение:

Используя формулу дисконтирования по сложной учетной ставке, определяем:

Заемщик может получить ссуду в размере 26’950 руб., а через два года вернет 55 тыс. руб.

Объединение платежей можно производить и на основе учетной ставки, например, при консолидировании векселей. В этом случае, сумма консолидированного платежа рассчитывается по следующей формуле:

где t_j – интервал времени между сроками векселей.

Пример. Вексель на сумму 10 тыс. руб. со сроком погашения 10.06, а также вексель на сумму 20 тыс. руб. со сроком погашения 01.08 заменяются одним с продлением срока до 01.10. При объединении векселей применяется учетная ставка 25%. Определить сумму консолидированного векселя.

Решение:

Для использования формулы консолидированного платежа необходимо определить срок пролонгации векселей:

Тогда, сумма консолидированного векселя:

Таким образом, сумма консолидированного векселя с датой погашения 01.10 составит 31’736 руб.

В том случае, когда учету подлежит долговое обязательство, по которому предусматривается начисление процентов, происходит совмещение начисления процентов по процентной ставке и дисконтирования по учетной ставке:

где PV₁ – первоначальная сумма долга;

PV₂ – сумма, получаемая при учете обязательства;

n₁ – общий срок платежного обязательства;

n₂ – срок от момента учета до погашения.

Пример. Обязательство уплатить через 100 дней сумму долга в размере 50 тыс. руб. с начисляемыми на нее точными процентами по ставке 40%, было учтено за 25 дней до срока погашения по учетной ставке 25%. Определить сумму, полученную при учете обязательства.

Решение:

Следует обратить внимание на различие временных баз, используемых при наращении и учете:

Следовательно, сумма, получаемая при учете данного обязательства, составит 54’516 руб.

Источник