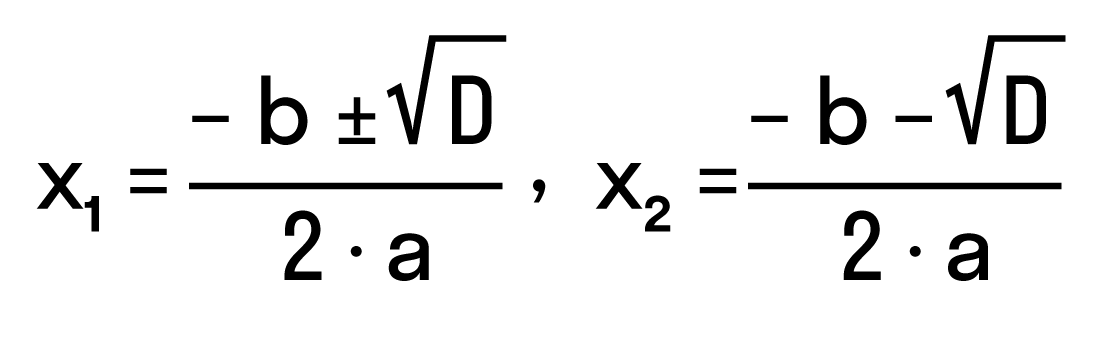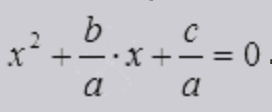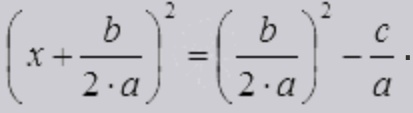дискриминант в каком классе изучают квадратного уравнения

Открытый урок по алгебре в 8 классе по теме «Дискриминант. Формула корней квадратного уравнения»

Ищем педагогов в команду «Инфоурок»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НИКОЛАЕВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА ТАТАРСКОГО РАЙОНА НОВОСИБИРСКОЙ ОБЛАСТИ

Конспект урока алгебры в 8 классе по теме

«Дискриминант. Формула корней квадратного уравнения»

Автор: Глинова Марина Михайловна,

учитель математики МБОУ Николаевской СОШ

Тип урока : урок ИНМ

Предметные: актуализировать знания обучающихся по теме «неполные квадратные уравнения», изучить и формировать умение применять формулы дискриминанта и корней при решении полных квадратных уравнений, совершенствовать вычислительные навыки,
формировать умения строить математические модели.

Личностные: развить познавательный интерес; формировать учебную мотивацию, адекватную самооценку, необходимость систематизации знаний; демонстрировать значимость математических знаний в практической деятельности.
Регулятивные: различать способ и результат действия, оценивать правильность выполнения действия, умение учиться и способность к организации своей деятельности; создать условия для развития умения анализировать, обобщать изучаемые факты, рефлексии способов и условий действия.

Познавательные: уметь строить математические модели (схемы), работать по алгоритму, работать с различными источниками информации.

Коммуникативные: уметь адекватно использовать речевые средства для аргументации своей позиции, уметь договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов, участвовать в коллективном обсуждении проблем.

Средства, обеспечивающие учебный процесс на уроке: компьютер, проектор, презентация, карточки с заданиями для групп.

1. Организационный момент: приветствие, проверка готовности.

2. Проверка домашнего задания.

3. Актуализация знаний учащихся по пройденной теме ( прием «Кубик Блума», «Математическое табло»)

— подводка к теме урока: прием «Составь слово»,
— постановка темы и целей урока,

— изучение формул корней квадратного уравнения, мини-исследование «Число корней полного квадратного уравнения»

5. Первичное закрепление изученного материала:
— решение уравнений обучающимися (работа у доски).

6. Контроль усвоения изученного.

7. Рефлексия. Подведение итогов урока.

8. Домашнее задание.

Технологическая карта урока:

1. Организационный момент.

Цель этапа: приветствие, проверка готовности к уроку, включение учащихся в учебную деятельность.

— Здравствуйте, ребята! Садитесь.

Урок я хочу начать притчей. Однажды молодой человек пришёл к

мудрецу и пожаловался ему: «Каждый день по 5 раз я произношу фразу «Япринимаю радость в мою жизнь, но радости в моей жизни нет».

Мудрец положил перед собой ложку, свечу и кружку и попросил: «Назови,что ты выбираешь из них».

Слушаю музыку, ведут диалог.

Подготавливаются к уроку, сдают тетради,

Мобилизация внимания, уважение к окружающим (Л)

2. Проверка домашнего задания

Цель этапа: формирование умения организации самостоятельной работы, контроль усвоения ранее изученного.

— Открываем тетради, проверка домашнего задания. Обменяйтесь тетрадями, возьмите ручку с пастой другого цвета. Обратите внимание на слайд, проверьте работу товарища, выставите оценку в соответствии с критериями.

— Обменяйтесь вновь тетрадями. Перенесите оценку за домашнюю работу на поля, обведите в кружок.

— Запишите в тетради число, классная работа.

Обмениваются тетрадями, проверяют и оценивают работу товарища.

Выносят оценку на поля

записывают число, классная работа в тетрадь.

Взаимоконтроль знаний, оценивание по критериям (Р)

3. Актуализация знаний учащихся.

Цель этапа: Повторение пройденного материала, контроль ранее изученного.

— Какую тему мы изучили?

— Посмотрим как вы усвоили теоретический материал:

Сейчас мы проверим уровень усвоения пройденного материала (прием «Кубик Блума»). Я предлагаю вам выйти и встать в круг. Бросая данный кубик своему товарищу, вы задаете ему теоретический вопрос. Ответив на него, он в свою очередь, кидает кубик и задает свой вопрос. Если отвечающий не может ответить, вопрос возвращается к хозяину, и задавший его должен дать полный ответ.

-Молодцы. Оцените себя по одному баллу за каждый правильно данный ответ. Вынесите оценку на поля

Проводят игру, отвечая на теоретические вопросы

Самооценка, выносят оценку на поля

Четко выражают свои мысли (К)

Определяют и формулируют основные теоретические знания (П)

— Обменяйтесь работами, возьмите ручку с пастой другого цвета. Обратите внимание на слайд, проверьте работу товарища, выставите оценку в соответствии с критериями.

— обменяйтесь тетрадями, вынесите оценку на поля.

Обмениваются тетрадями, проверяют и оценивают работу товарища.

Выносят оценку на поля

Применение знаний на практике (П)

Взаимоконтроль знаний, оценивание по критериям (Р)

Цель этапа: формирование нового знания

Подводка к теме урока: прием «Составь слово»

— Во время работы, не забываем о правилах поведения в группе.

— Работа закончена. Обменяйтесь карточками между группами, проверьте работу товарищей, подсчитайте количество правильных ответов.

— Оцените работу группы в соответствии с критериями. Вынесите оценку на поля.

Образуют группы, совместно вычисляют значения выражений, содержащих квадратные корни.

Проверяют работу другой группы, подсчитывают кол-во правильных ответов.

Выносят оценку на поля

Планируют свою деятельность в группе (Р), Выражение своих мыслей; аргументация своего мнения (К);

Осуществление взаимоконтроля и взаимопомощи (К)

Постановка темы и целей урока:

— Ребята, соотнесите свои ответы с таблицей букв.

— Какое слово получили? Вы знаете, что оно означает?

— Давайте обратимся к словарям (толкование слова)

— Как обозначается дискриминант?

— Посмотрите на слайд: какое уравнение здесь лишнее? По какому признаку вы выделили именно его?

— Сформулируйте тему урока. Каковы будут цели урока?

Отвечают на вопросы учителя, разбирают толкование слова

Определяют лишнее как полное уравнение

Определяют тему и цели урока, записывают в тетрадь тему

Определяют толкование слова (П)

Четко выражают свои мысли (К)

Физминутка: Верное утверждение – встали, неверное – сели.

ИНМ: Изучение формул корней квадратного уравнения, мини-исследование «Число корней полного квадратного уравнения», формула дискриминанта.

— Ребята, обратите внимание на формулы корней квадратного уравнения.

— Чем в этих формулах является дискриминант?

— Какова область определения дискриминанта, как подкоренного выражения?

— Значит можно сделать предположение, что значение дискриминанта определяет количество корней полного квадратного уравнения.

— Как вы думаете, сколько корней может иметь полное квадратное уравнение?

А помочь вам в этом может учебник. Обратитесь к стр. 124-125 и заполните схему.

— Озвучьте результаты вашего мини-исследования.

Молодцы, мы разобрали с вами все вопросы.

— Давайте запишем формулу дискриминанта себе в тетрадь.

Отвечают на вопросы учителя (подкоренным выражением)

Делают свои предположения

Четко выражают свои мысли (К)

Выдают предположение, Определяют и формулируют основные теоретические знания (П)

5. Первичное закрепление изученного материала:
Цель этапа: организация усвоение нового знания с проговариванием во внешней речи.

— Отработаем применение новых знаний на практике. Я предлагаю решить несколько уравнений у доски. Есть желающие? А работать мы будем с помощью алгоритма (на слайде).

Работа у доски двух обучающихся

Работа по алгоритму, регуляция приемами контроля и самоконтроля (Р)

Применение усвоения знаний на практике (П)

6. Контроль усвоения изученного.

Цель этапа: первичный контроль усвоения нового материала.

— А сейчас я предлагаю каждому из вас решить квадратное уравнение. Алгоритм решения на слайде, подробный пример решения в тетради. Желаю удачи.Можете приступать к работе.

— Обменяйтесь тетрадями, проверьте результаты работы товарища, выставьте оценку в соответствии с критериями.

— Верните тетради товарищу. Вынесите оценки на поля.

Применение знаний на практике (П)

Осуществление взаимоконтроля (Р)

6. Рефлексия. Подведение итогов урока.

Цель этапа: фиксация нового содержание урока, организация рефлексии и самооценки учениками собственной учебной деятельности.

— Какова была тема урока? Цели урока? Достигли ли вы этих целей?

— Что вам более всего удалось, какие моменты были выполнены наиболее успешно?

— Перечислите основные трудности, которые вы испытывали во время урока. Что помогло их преодолеть?

— Оцените свою работу: найдите среднее арифметическое оценок, заработанных на разных этапах урока. Каковы результаты? Поднимите руки те, кто получил за урок оценку «5», «4», «3», «2». Молодцы.

Подводят итого урока, определяют степень достижения поставленных целей

Выражение своих мыслей; аргументация своего мнения (К);

7. Домашнее задание: пункт 22, №534 (а-е), 577. Творческое задание (дополнительное на оценку) – составить кроссворд по теме «Квадратные уравнения»

Достают дневники и записывают домашнее задание.

— Ребята, в заключении урока я хочу провести с вами небольшую игру-загадку. Встаньте, пожалуйста. И если вы не против, я предлагаю нашим гостям также в этой игре поучаствовать. Правила игры таковы, я читаю строку стихотворения, а вы должны закончить словом-отгадкой. Готовы? Начинаем:

На уроке каждый проявил …. (СТАРАНИЕ)

Показал реальные свои по теме …. (ЗНАНИЯ)

Остается нам в такие вот …… (МОМЕНТЫ)

Подарить друг другу громкие…….(АПЛОДИСМЕНТЫ)

Надеюсь, что сегодня вы вняли совету мудреца: протянули руку и взяли новые знания.

-Молодцы! Спасибо вам, ребята, за работу; гостям, за то, что смогли найти время и прийти к нам на урок. Урок окончен!

Алгебра. 8 класс. Учебник для общеобразовательных учреждений. Ю.Н,Макарычев, Н.Г.Миндюк и др. М., «Просвещение», 2015.

Источник

В каком классе проходят дискриминант?

В каком классе изучают дискриминант?

Дискриминант изучают в 8 классе, примерно в третьей четверти

Замечательная вещь Александра Куприна!

А знаете, как учителя его расшифровывали – Учитель Пришел ЕДва Домой, Голодный, Измученный, Злой. И во многом они были правы. Это про жизнь учительскую

И потом, что вы так упираетесь в информационные технологии. По-моему пора ограничивать «компьютеризацию» образования. Компьютером пытаются подменить живого учителя и в итоге растят каких-то киборгов, без чувств, без мыслей.

Никакой компьютер НИГДЕ, НИКОГДА И НИКАК не заменит живого слова учителя!

Уж поверьте. Всю сознательную жизнь наблюдаю за учителями как снаружи (сам учился), так и изнутри (отец почти 40 лет проработал учителем и супруга – более 30-ти лет)

Так что, дорогие учителя, пользуйтесь компьютером, Интернетом, интерактивными досками и т. п., но не давайте им себя заслонить.

Потому, что в связи с программами увеличения рождаемости сначала не хватало детских садов и яслей, а сейчас не хватает школ для юных россиян. Многие школы переполнены, занятия идут в две смены. Особенно остро возникает эта проблема в новых микрорайонах, где много молодых семей, а инвесторы стремятся больше заработать именно на жилье, а не на социальных объектах. Вместе с тем, в старых районах, в сельской местности, в моногородах, где нет работы и люди вынуждены уезжать, школы не заполнены и их закрывают или укрупняют, детей возят на школьных автобусах из многих населенных пунктов в один.

Полагаю, вместе с демографическими программами нужно еще предусмотреть программу равномерного заселения территории. В советское время молодежь привлекали на комсомольские стройки, на целину, на БАМ. Сейчас нужно что-то подобное, только на другом, современном уровне, пассионарность молодежи нужно направлять на созидание, чтобы они чувствовали себя хозяевами своей жизни, а не скучивались в крупных городах и жестко конкурировали.

Как вариант возьмите для себя литературу в библиотеке или просто купите. Зато будете всегда обладать актуальными знаниями, подготавливая себя как раз по программе ЕГЭ-2017 года. Здесь вы можете купить любой материал литературы, для ЕГЭ и не бояться, что информация не по программе составлена!

Слово «ученица» является существительным женского рода, будет отвечать на вопрос «кто?».

Разберем данное слово по составу, проведем морфемный разбор.

Источник

Урок алгебры в 8-м классе «Квадратные уравнения»

Разделы: Математика

Тип урока: урок обобщения и систематизации знаний. Углубленное изучение свойств квадратных уравнений.

I. Организационный момент

1) … уравнением называется уравнение ax 2 + bx + c = 0, где a, b, c – заданные числа, а =/=0, х – переменная.
2) Уравнение х 2 = а, где а > 0, имеет корни х₁ = … х₂ = …
3) Уравнение ах 2 = 0, где а =/= 0, называют … квадратным уравнением.
4) Если ax 2 + bx + c = 0 квадратное уравнение (а =/= 0), то b называют … коэффициентом.
5) Корни квадратного уравнения ax 2 + bx + c = 0 вычисляют по формуле х₁,₂ = …
6) Приведенное квадратное уравнение x 2 + px + q = 0 совпадают с уравнением общего вида, в котором а = …, в = …, с = …
7) Если х₁ и х₂ – корни уравнения x 2 + px + q = 0, то справедливы формулы х₁ + х₂ = … х₁ x х₂ …

1) Если ax 2 + bx + c = 0 квадратное уравнение, то b называют … коэффициентом, с – … членом.
2) Уравнение х 2 = а, где а 2 + с = 0, где а =/= 0, c =/= 0, называют … квадратным уравнением.
4) Корни квадратного уравнения аx 2 + bx + c = 0 вычисляют по формулам х₁ = …, х₂ = …
5) Квадратное уравнение ax 2 + bx + c = 0 имеет два различных действительных корня, если b 2 – 4ac … 0.
6) Квадратное уравнение вида x 2 + px + q = 0 называют …
7) Сумма корней приведенного квадратного уравнения равна … коэффициенту, взятому с … знаком, а произведение корней равно … члену.

Задание (устно) на определение вида уравнения.

Вопрос. Ребята, здесь вы видите уравнения, определенные по какому-то признаку. Как вы думаете, какое из уравнений группы является лишним?

а) 1) 2х 2 – х = 0 б) 1) х 2 – 5х + 1 = 0
2) х 2 – 16 = 0 2) 9х 2 – 6х + 10 = 0
3) 4х 2 + х – 3 = 0 3) х 2 + 2х – 2 = 0
4) 2х 2 = 0 4) х 2 – 3х – 1 = 0

– Как можно решить приведенное квадратное уравнение?
– Сформулировать теорему Виета.
– Как используется теорема Виета при решении квадратного уравнения общего вида ax 2 + bx + c = 0.

А сейчас, ребята, послушайте стихотворение о теореме Виета:

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше скажи постоянства такого:
Умножишь ты корни и дробь уж готова?
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе b, в знаменателе а.

III. Решение задач с использованием теоремы Виета (прямой и обратной)

1-е задание.

Дано уравнение х 2 – 6х + 5 = 0.

2-е задание (устно).

3-е задание

Составить приведенное квадратное уравнение, если известны его корни.

х₁ = – 3, х₂ = 1, х₁ + х₂ = – 3 + 1 = – 2, – р = – 2, р = 2
х₁ x х₂ = – 3 x 1 = – 3, q = – 3, x 2 + px + q = 0, х 2 + 2х + (– 3) = 0, х 2 + 2х – 3 = 0
получили приведенное квадратное уравнение.

б) А теперь самостоятельно по вариантам составить приведенное квадратное уравнение.

Во время самостоятельной работы два ученика работают у доски по карточкам.

Карточка №1 Карточка №2

Составить приведенное квадратное уравнение, если известны его корни:

После самостоятельной работы сделать вывод о знаке перед свободным членом квадратного уравнения.

IV. Изучение нового свойства квадратных уравнений

1. Ребята, мы с вами решали квадратные уравнения различными способами: выделением квадрата двучлена, по формуле корней, с помощью теоремы Виета, и каждый раз убеждались в том, что уравнение можно решить легче и быстрее. Сегодня мы познакомимся еще с одним способом решения, который позволит устно и быстро находить корни квадратного уравнения.

При решении некоторых квадратных уравнений, оказывается, немаловажную роль играет сумма коэффициентов. Рассмотрим это на уравнениях, которые вы решили дома.

V. Проверка домашнего задания

Учитель делает выводы вместе с учениками.

VI. Решение задач на закрепление свойства

1. По учебнику № 534 (а, б, д),
2. Обратить внимание на уравнение, которое было решено в начале урока

Сделать вывод о значимости данного свойства.

VII. Самостоятельная работа

Учитель выставляет оценки за урок.

Источник

Как решать квадратные уравнения

Понятие квадратного уравнения

Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Есть три вида квадратных уравнений:

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.

Давайте-ка на примерах — вот у нас есть два уравнения:

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению ax 2 + c = 0, которое:

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

0,5x = 0,125,
х = 0,125/0,5

Ответ: х = 0 и х = 0,25.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Пифагора: x 2 − 6x + 8 = 0.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax 2 + bx + c = 0. Выполним ряд равносильных преобразований:

,

после чего уравнение примет вид

Так, мы пришли к уравнению , которое полностью равносильно исходному ax 2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник