для каких матриц применимы понятия определителя и обратной матрицы

ЧАВО по матрицам и кватернионам (3 стр)

Что такое определитель матрицы?

Определитель матрицы это число, которое показывает, есть ли у матрицы обратная или нет. Если определитель равен 0, то обратной матрицы нет, иначе обратная матрица существует.

Если элемент, а соответственно и определитель, не равен 0, то обратная матрица существует.

В случае единичной матрицы ее значение будет 1/1 или 1.0

Однако, если это число 0, то и определитель тоже 0.

При попытке найти обратное от нуля, получаем бесконечность. Так делать нельзя, так что для 0 не существует обратной матрицы.

Для единичной матрицы определитель всегда равен 1. Все матрицы с определителем равным единице называют изотропными.

Поэтому все матрицы вращения изотропны, так как определитель всегда равен 1.0.

Как мне посчитать определитель матрицы?

Определитель матрицы считается при помощи правила Крамера,
где каждое число может быть рассчитано
через разбиение матрицы в более малые матрицы.

Для матриц размером 3х3 и 4х4, найти определитель сложнее,
но все равно можно при помощи методов типа правила Крамера.

Что такое изотропная и анизотропная матрицы?

Изотропной матрицей называют матрицу, в которой сумма квадратов всех трех строк или колонок равна 1.

Матрицы, в которой это не происходит, называется Анизотропной.

Матрицы используются для того, чтобы поворачивать и скалировать объект, иногда может быть необходимо, увеличивать или сжимать по одной оси сильнее, чем по другим.

К примеру, в сейсмических задачах, необходимо увеличить ось Z на 50 или более, при этом оси X и Y нужно оставить неизменными.

Другим примером может служить «раздавливание» и «растягивание» в анимации персонажей. Когда персонаж ударяет тяжелый предмет типа наковальни, то необходим эффект, при котором персонаж растягивается в стороны и сдавливается вертикально:

Матрица будет выглядеть так:

Однако здесь появляется проблема. В то время как не будет проблем с обработкой вершин, мы получим неправильное освещение, из-за кривых нормалей.

На шаге обработки данных, трансформация, выраженная данной матрицей Изменит как вершины, так и нормали.

После такого умножения, все нормали перестанут быть нормализованными, что подействует на освещение и обратное отсечение.

Что такое обратная матрица?

где I единичная матрица.

Так что, в результате умножения матрицы на обратную к ней будет единичная матрица. Однако матрица должна удовлетворять нескольким условиям, перед тем как обратная матрица будет посчитана.

Во-первых, ширина и высота матрицы должны совпадать, во-вторых ее определитель не должен равняться 0.

Расчет обратной матрицы необходим для реализации обратной кинематики с помощью сплайнов.

Как мне посчитать обратную матрицу?

В зависимости от размера матрицы, расчет обратной может быть простым или очень сложным.

К примеру, обратная 1х1 матрица это просто обратная от одного элемента:

Решение 2х2 матриц и больших может быть получено при использовании правила Крамера или через решение системы уравнений.

Однако, для конкретных случаев, таких как единичная матрица или матрицы поворота, обратная матрица сразу известна или может быть получена транспонированием.

Как мне посчитать обратную матрицу от единичной матрицы?

Обратная единичной матрицы и есть единичная матрица.
\(I*I^ <-1>= I\)
У любой единичной матрицы определитель всегда равен 1.

Как мне посчитать обратную от матрицы вращения?

Так как определитель матрицы вращения равен 1,
то расчет обратной матрицы равен транспонированию.

Альтернативно, если известны углы поворота, то можно взять их с минусом,
для расчета новой матрицы вращения.

Как мне посчитать обратную матрицу при помощи правила Крамера?

Дана 3×3 матрица M:
\(M=\(\matrix\)
То ее определитель считается так:
\(detM=sum_^n M*submat_<0,i>M*-1^\)
где:

В этом случае, значение каждого элемента можно определить так:

Как мне посчитать обратную от 2х2 матрицы?

Для матриц 2х2, расчет несколько сложнее. Если матрицы определена так:

И обратная делается так:

Как мне посчитать обратную от 3х3 матрицы?

Для матриц 3х3 и больше, обратная считается с помощью правила Крамера
или через решение системы линейных уравнений.

Если правило Крамера применить к матрице М:

Как мне посчитать обратную 4х4 матрицы?

Также как с матрицами 3х3, нужно применить правило Крамера или решить линейные уравнения.

Эффективно будет использовать уже описанные Сишные функции,
которые использовались при расчете обратной к 3х3 матрице.

Чтобы реализовать правило Крамера для матриц 4х4, необходимо выделить
отдельные подматрицы. Это достигается при помощи следующей функции:

Обратная матрица может быть рассчитана так:

обратную любой 4х4 матрицы. Их применение включает возможность посчитать
основную матрицу для сплайнов, обратить вращение и
перестроить матричные уравнения.

Источник

Для каких матриц применимы понятия определителя и обратной матрицы

Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:

Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка.

.

Для определителя третьего порядка проверьте самостоятельно.

Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.

Доказательство проводится проверкой, как и свойство 1. (Самостоятельно)

.

.

Докажем это равенство, используя предыдущие свойства определителя.

Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.

АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ

Пусть имеем определитель третьего порядка: .

Минором, соответствующим данному элементу a_ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу a_ij будем обозначать M_ij.

Например, минором M₁₂, соответствующим элементу a₁₂, будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a₁₂, берётся со знаком “–”, т.е. можно записать, что

.

(1)

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическое дополнение элемента a_ij обозначается A_ij.

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A_ij = (–1) i+j M_ij.

Например,

Пример. Дан определитель . Найти A₁₃, A₂₁, A₃₂.

Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

.

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:

Разложим полученный определитель по элементам 1-ой строки.

.

(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a₂₁, a₂₂, a₂₃. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

ОБРАТНАЯ МАТРИЦА

Понятие обратной матрицы вводится только для квадратных матриц.

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Прежде всего заметим, что можно доказать следующее свойство определителей .

Предположим, что |A| = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что |A| ≠ 0.

Покажем, что в этом случае обратной матрицей будет матрица

, где A_ij алгебраическое дополнение элемента a_ij.

Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c₂₂ = c₃₃ = 1.

Кроме того, все недиагональные элементы матрицы C равны нулю. Например,

Таким образом, теорема содержит способ нахождения обратной матрицы.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

Итак, чтобы найти обратную матрицу нужно:

Аналогично для матриц второго порядка, обратной будет следующая матрица .

|A| = 2. Найдем алгебраические дополнения элементов матрицы A.

.

.

Вычислим |A| = 4. Тогда .

.

Источник

Определители и их свойства. Обратная матрица. Ранг матрицы

Понятие определителя возникло в связи с задачей решения систем линейных уравнений.

Определитель матрицы А = (а _{i j}) есть некоторое число, равное алгебраической сумме из n! произведений, построенных из элементов матрицы по определенным правилам.

Обозначение: определитель матрицы Аобозначается следующим образом

= Δ.

Рассмотрим определители 2-го и 3- го порядков.

Определение 15. Определителем 2-го порядка, соответствующим

квадратной матрице А = , называется число

Определение 16. Определителем 3-го порядка, соответствующим

квадратной матрице 3-го порядка А =

называется число, равное

Такой способ вычисления определителя называется «разложением определителя по первой строке».

В дополнение к этому для вычисления определителя третьего порядка можно воспользоваться также «правилом треугольников», которое символически записывается следующим образом

Пример 9. Вычислить .

Решение. Способ 1 – методом «разложения по первой строке»:

Способ 2 – по «правилу треугольников»:

Общим методом вычисления определителей 3-го и более высоких порядков является метод разложения определителя по любой строке или по любому столбцу. Для этого требуется ввести новые понятия.

Определение 17. Минором к-го порядка произвольной матрицы А

называется определитель, составленный из элементов

матрицы, расположенных на пересечении каких-либо k строк и

Для матрицы А = можно указать, например, такие миноры 2- го порядка: и т. д., и миноры 3- го порядка :

, , и .

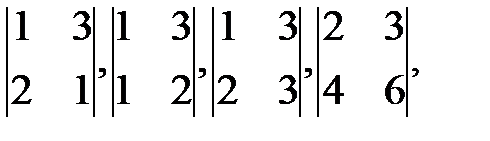
Миноров более высокого порядка у матрицы нет.

Определение 18. Минором М _{i j} к элементу а _{i j} определителя квадратной

матрицы А называется определитель, полученный из

данного вычеркиванием i-й строки и j-го столбца.

Для матрицы А= минор М_{3 2} равен М_{3 2} = .

Определение 19. Алгебраическим дополнением А_{i j} к элементу а _{i j}

квадратной матрицы А называется число

А_{i j} = .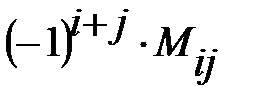

Пример 10. Найти А_{2 3} для матрицы из примера 9 :

Пример 11. Вычислить определитель detA = 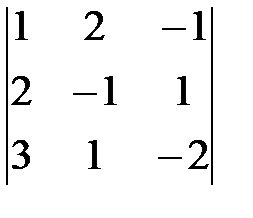, разложив его:

а) по элементам второй строки; б) по элементам первого столбца.

а) detA = 2(-1) 2+1 × (-1)(-1) 2+2 × + 1× (-1) 2+3 × =

б) detA = 1(-1) 1+1 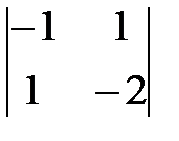+ 2(-1) 2+1 + 3(-1) 3+1 =

При вычислении определителей полезно знать свойства определителей. Это позволит упростить вычисление определителя.

Свойства определителей

1. Определитель квадратной матрицы А не меняется при ее

2. При перестановке местами каких- либо двух строк ( или столбцов)

определитель сохраняет абсолютную величину, но меняет знак на противоположный.

3. Определитель квадратной матрицы, имеющей две одинаковые сроки (или столбца), равен нулю.

4. Умножение всех элементов некоторой строки (или столбца) определителя

на число l равносильно умножению определителя на это число l.

5. Если элементы некоторой строки (или столбца) равны нулю, то определитель равен нулю.

6. Если к элементам некоторой строки (или столбца ) определителя прибавить соответствующие элементы какой-либо другой строки (или столбца), умноженные на произвольное число l, то величина определителя не изменится.

7. Если элементы каких-либо двух строк (или столбцов) определителя пропорциональны или равны, то определитель равен нулю.

Пример 12. Вычислить определитель det A = , сведя его вычисление к вычислению одного определителя 2-го порядка.

Решение. 1) используя свойство 6, прибавим к элементам первого столбца соответствующие элементы третьего столбца. Получим определитель ;

2) к элементам второго столбца прибавим соответствующие элементы третьего столбца, умноженные на 2, в итоге получим определитель , который

легко вычисляется разложением по первой строке

Обратная матрица

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной в противном случае.

А * = .

Матрица ( А * ) Т называется присоединенной матрицей:

( А * ) Т =

Пример 13. Вычислить обратную матрицу к матрице .

Запишем (А * ) Т =

Определитель матрицы А был вычислен ранее и равен det A = 10. Тогда обратная матрица будет

Определители двух взаимно обратных матриц являются взаимно обратными числами

Ранг матрицы

Пусть задана матрица Аразмером m´n, где m – число строк, а n – число столбцов матрицы, и пусть m

Источник