для каких рядов распределения применяют гистограммы
Графическое изображение рядов распределения
Анализ рядов распределения можно проводить на основе их графического изображения. Линейчатые и круговые диаграммы строятся для отображения структуры совокупности.
Применяются вместе с диаграммами и такие линии, как полигон, кумулята, огива, гистограмма.
При изображении дискретных вариационных рядов используется полигон.
Полигон– ломаная кривая, строится на основе прямоугольной системы координат, когда по оси Х откладываются значения признака, а по оси У – частоты.
В прямоугольной системе координат строят точки с координатами (x1, f1), (x2, f2), …, (xN, fN), затем последовательно соединяют их отрезками, а из первой и последней точек опускают перпендикуляры на ось х. Полученный многоугольник является полигоном дискретного вариационного ряда.
Пример построения полигона
| Количество баллов x |
| Число учащихся n |
Задание: построить полигон частот.
Решение.
Строим точки, основываясь на данных из таблицы. Полученные точки соединяем отрезками прямой. Обратите внимание на точки (0; 0) и (13; 0), расположенные на оси абсцисс и имеющие своими абсциссами числа, на 1 меньшее и большее, чем соответственно абсциссы самой левой и самой правой точек. Полигон частот изображен на рисунке.
Гладкая кривая, соединяющая точки– это эмпирическая плотность распределения.
Интервальный вариационный ряд изображают в виде гистограммы (частный случай столбиковой диаграммы). Для ее построения для интервальных рядов с равными интервалами в прямоугольной системе координат по оси абсцисс откладывают отрезки, равные длине интервала. Затем на этих отрезках, как на основаниях, строят прямоугольники, высота которых пропорциональна частоте или частости. Для интервального ряда с неравными интервалами по оси ординат откладывают плотность распределения, так как в этом случае именно она дает представление о заполненности интервала. Площадь всей гистограммы численно равна сумме частот.
Пример построения гистограммы.
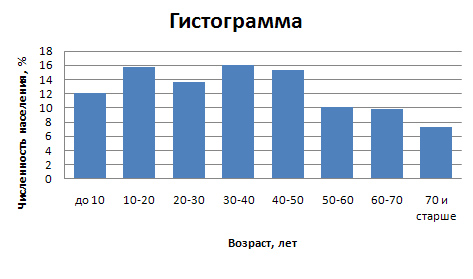
Гистограмма распределения населения России по возрастным группам.
| Все население | В том числе в возрасте | ||||||||
| до 10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70 и старше | Всего | |
| Численность населения | 12,1 | 15,7 | 13,6 | 16,1 | 15,3 | 10,1 | 9,8 | 7,3 | 100,0 |
Кумулята– ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси Х откладываются значения признака, а по оси У – накопленные частоты. Накопленные частоты наносятся в виде ординат. Соединяя вершины отдельных ординат отрезками прямой, получаем ломаную линию, имеющую неубывающий вид.
Для дискретных рядов на оси откладываются сами значения признака, а для интервальных – середины интервалов.
| Размер заработной платы руб в месяц Xi | Численность работников чел. fi | Накопленные частоты S |
| до 5000 | ||
| 5000 — 7000 | ||
| 7000 — 10000 | ||
| 10000 — 15000 | ||
| Итого: | — |
Рассчитаем накопленные частоты:
Наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.
При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:
Статистические таблицы
В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.
Статистическая таблица– это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица позволяет охватить материалы статистической сводки в целом, она также является системой мыслей об исследуемом объекте, излагаемых цифрами на основе определенного порядка в расположении систематизированной информации.
Статистическая таблица – это система строк и столбцов, в которых в определенной последовательности и связи излагается статистическая информация о социально-экономических явлениях.
По внешнему виду статистическая таблица представляет собой ряд пересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали – графы (столбцы, колонки), которые в совокупности составляют как бы скелет таблицы.
В образовавшиеся внутри таблицы клетки записывается информация. Составленную таблицу принято называть макетом таблицы,в котором мысленно определяются в деталях цель обследования, объем разработки материалов сводки.
Статистическая таблица имеет свое подлежащее и сказуемое.
Подлежащее таблицыпоказывает, о каком явлении идет речь в таблице, и представляет собой группы и подгруппы, которые характеризуются рядом показателей. Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь в таблице, т. е. перечень отдельных или всех единиц совокупности либо их групп. Чаще всего подлежащее помещается в левой части таблицы и содержит перечень строк.
Сказуемым таблицыназываются числовые показатели, с помощью которых характеризуется объект, т. е. подлежащее таблицы.
Показатели, образующие подлежащее, располагают в левой части таблицы, а показатели, составляющие сказуемое, помещают справа.
Составленная и оформленная статистическая таблица должна иметь общий, боковые и верхние заголовки. Общий заголовок обычно располагается над таблицей и выражает ее основное содержание. Помещенные слева боковые заголовки раскрывают содержание строк подлежащего, а верхние – вертикальных граф (сказуемого таблицы),
В коммерческой деятельности разрабатываются и составляются различные статистические таблицы
В зависимости от построения подлежащего таблицы делятся на три вида: простые, групповые и комбинационные.
1.1. Простые таблицы не содержат в подлежащем систематизации изучаемых единиц статистической совокупности. В подлежащем простой таблицы объект изучения не подразделяется на группы, а дается либо перечень всех единиц совокупности, либо указывается совокупность в целом.
По характеру представляемого материала простые таблицы бывают собственно перечневые, территориальные и хронологические.
Если в подлежащем таблицы содержится простой перечень каких-либо объектов, таблица называется простой перечневой.
Таблицы, в подлежащем которых приводится перечень территорий (районов, областей и т. п.), называются перечневыми территориальными.
Хронологическую таблицу можно составлять за любые по величине отрезки времени или на моменты, отстоящие друг от друга по времени на различную длину.
1.2. Групповые таблицысодержат в подлежащем группировку единиц объекта наблюдения по одному существенному признаку, а в сказуемом указываются число единиц в группах (абсолютное или в процентах) и сводные показатели по группам. Простейшим видом групповой таблицы являются таблицы, в которых представлены ряды распределения. Групповая таблица может быть более сложной, если в сказуемом приводится не только число единиц в каждой группе, но и ряд других важных показателей, количественно и качественно характеризующих группы подлежащего. Такие таблицы часто используются в целях сопоставления обобщающих показателей по группам, что позволяет сделать определенные практические выводы.
Групповые статистические таблицы дают более информативный материал для анализа изучаемых явлений благодаря образованным в их подлежащем группам по существенному признаку или выявлению связи между рядом показателей.
1.3. Комбинационныминазывают статистические таблицы, которые имеют в подлежащем группировку по двум или более группировочным признакам, связанным между собой. В подлежащем комбинационной таблицы совокупность подразделяется на группы не по одному, а по нескольким признакам. Комбинационная таблица устанавливает взаимное действие на результативные признаки (показатели) и существующую связь между факторами группировки.
С помощью групповых и комбинационных таблиц можно изучать состав явлений, а также связь и зависимость числовых показателей сказуемого от группировочных признаков подлежащего.
Одними из ответственных моментов построения статистических таблиц являются разработка сказуемого, определение его содержания, правильное установление связи между группировочными признаками и показателями, их характеризующими.
Сказуемое, находясь во взаимосвязи с подлежащим таблицы, должно быть построено так, чтобы с помощью системы его показателей можно было получить полную характеристику выделенных групп, охватить их существенные черты.
Сказуемое статистических таблиц бывает простым и сложным. При простой разработке показатели сказуемого располагаются последовательно один за другим. Распределяя показатели на группы по одному или нескольким признакам в определенном сочетании, получают сложное сказуемое.
Графическое изображение рядов распределения: полигон, гистограмма. Показатели центра распределения, колеблемости признака. Формы распределения.
Поможем написать любую работу на аналогичную тему
Графики являются наглядной формой отображения рядов распределения. Для изображения рядов применяются линейные графики и плоскостные диаграммы, построенные в прямоугольной системе координат.
Для графического представления атрибутивных рядов распределения используются различные диаграммы: столбиковые, линейные, круговые, фигурные, секторные и т. д.
Для дискретных вариационных рядов графиком является полигон распределения.
Полигоном распределения называется ломаная линия, соединяющая точки с координатами 




График строится в принятом масштабе. Вид полигона распределения приведен на рис. 5.1.
При построении графиков рядов распределения большое значение имеет соотношение масштабов по оси абсцисс и оси ординат. В этом случае и необходимо руководствоваться «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания.
При проведении эмпирического исследования ряда распределения рассчитываются и анализируются следующие группы показателей:
• показатели положения центра распределения;
• показатели степени его однородности;
• показатели формы распределения.
Показатели положения центра распределения. К ним относятся степенная средняя в виде средней арифметической и структурные средние – мода и медиана.
Средняя арфметическая для дискретного ряда распределения рассчитывается по формуле:
В отличие от средней арифметической, рассчитываемой на основе всех вариант, мода и медиана характеризует значение признака у статистической единице, занимающей определенное положение в вариационном ряду.
Медиана (Me) — значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.
Медиану используют как наиболее надежный показатель типичного значения неоднородной совокупности, так как она нечувствительна к крайним значениям признака, которые могут значительно отличаться от основного массива его значений. Кроме этого, медиана находит практическое применение вследствие особого математического свойства: 
Данные приведены в таблице 5.2.
Мода выбирается по максимальному значению частоты: при nmax = 14 Mo=4, т.е. чаще всего встречается 4-ый разряд. Для нахождения медианы Me определяются центральные единицы 
Мода определяется следующим образом:
• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.
• Внутри модального интервала значение моды вычисляется по формуле:
Для расчета медианы в интервальных рядах используется следующий подход:
• По накопленным частотам находится медианный интервал. Медианным называется интервал, содержащий центральную единицу.
• Внутри медианного интервала значение Me определяется по формуле:
В неравноинтервальных рядах при вычислении Mo используется другая частотная характеристика – абсолютная плотность распределения:
Расчет моды и медианы для интервального ряда распределения рассмотрим на примере ряда распределения рабочих по стажу, приведенного в таблице 5.3.
• Максимальная частота n max = 13, она соответствует четвертой группе, следовательно, модальным является интервал с границами 12 – 16 лет.
• Моду рассчитаем по формуле:
Чаще всего встречаются рабочие со стажем работы около 13 лет. Мода не находится в середине модального интервала, она смещена к его нижней границе, связано это со структурой данного ряда распределения (частота предмодального интервала значительно больше частоты постмодального интервала).
• По графе накопленных частот определяется медианный интервал. Он содержит 25 и 26-у статистические единицы, которые находятся в разных группах – в 3-ей и 4-ой. Для нахождения Me можно использовать любую из них. Расчет проведем по 3-ей группе:
Такое же значение Me можно получить при её расчете по 4-ой группе:
Для нахождения моды в интервальном ряду правую вершину модального прямоугольника нужно соединить с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.
Для определение медианы высоту наибольшей ординаты кумуляты, соответствующей общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.
Кроме Mo и Me в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения. Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:
• квартили 
• децили 
Рассчитаем квартили для ряда распределения рабочих участка по стажу работы:
Следовательно, у четверти рабочих стаж менее 7 лет и у четверти – более 16 лет. Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значение признака, мода, медиана.
При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:
• для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых
• для неустойчивых процессов положение центра распределения характеризуется с помощью Mo или Me. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку занимает положение между средней арифметической и модой.
Вторая важнейшая задача при определении общего характера распределения – это оценка степени его однородности. Однородность статистических совокупностей характеризуется величиной вариации (рассеяния) признака, т.е. несовпадением его значений у разных статистических единиц. Для измерения вариации в статистике используются абсолютные и относительные показатели. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.
Из математической статистики известно, что при увеличении объема статистической совокупности 

В статистике различают следующие виды кривых распределения:
• одновершинные кривые; • многовершинные кривые.
Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки.
Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.
Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях
Для характеристики асимметрии используют коэффициенты асимметрии.
Наиболее часто используются следующие из них:
• Коэффициент асимметрии Пирсона
Рис. 5.4.Правосторонняя асимметрия Рис. 5.5. Левосторонняя асимметрия
Чем ближе по модулю As к 1, тем асимметрия существеннее:
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка:
Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.
Центральный момент k-ого порядка рассчитывается как:
Соответственно формулы для определения центрального момента третьего порядка имеют следующий вид:
Для оценки существенности рассчитанного вторым способом коэффициента асимметрии определяется его средняя квадратическая ошибка:
Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцесс является показателем островершинности распределения. Он рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка
При симметричных распределениях Ех=0. если Ех>0, то распределение относится к островершинным, если Ех