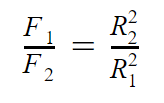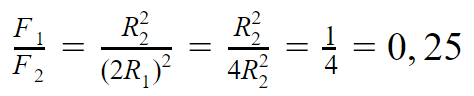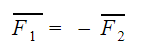для каких тел применим закон всемирного тяготения

Закон всемирного тяготения Ньютона

На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения (см. Законы механики Ньютона), он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.

Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории. Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение тел, падающих на поверхность Земли, они были уверены, что наблюдают явление чисто земной природы — существующее только недалеко от поверхности нашей планеты. Когда другие ученые, например Иоганн Кеплер (см. Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.

Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.

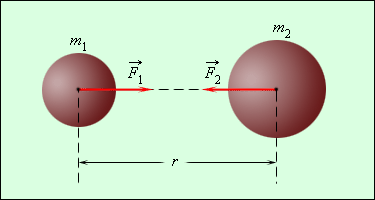
Результаты ньютоновских расчетов теперь называют законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:

Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на все без исключения физические материальные тела во Вселенной. В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.

Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на вас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и вы ее реально ощущаете как свой вес. Если вы что-нибудь уроните, оно под действием всё той же силы равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой g.

Наконец, закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.

Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.

Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.

Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.

Источник

Закон всемирного тяготения

Гравитационное взаимодействие

Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.

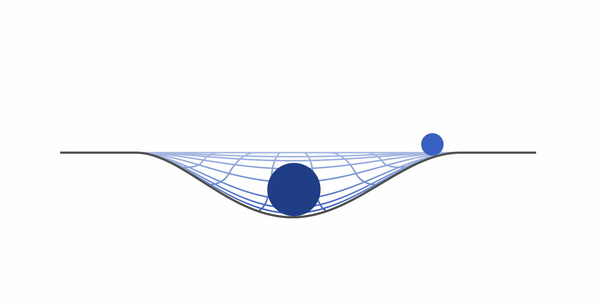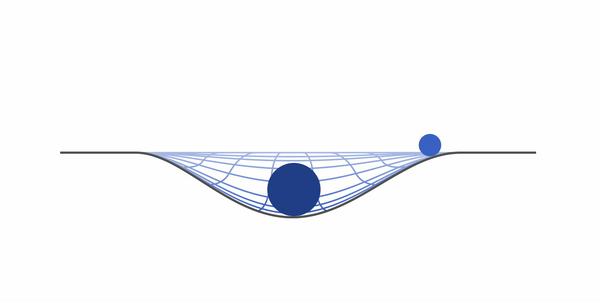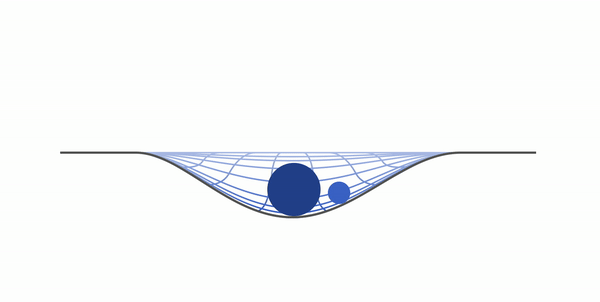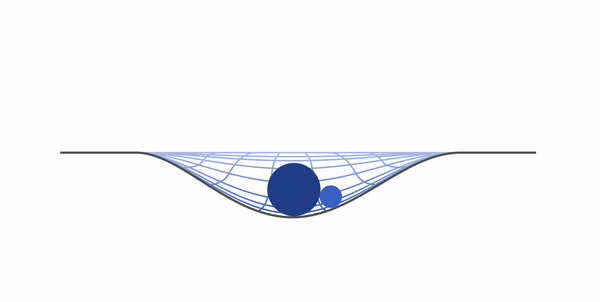
Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:

Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).

Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.

Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.

Закон всемирного тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.

Задачка раз

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?

Решение

По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:

По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R₁=2R₂.

Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.

Задачка два

У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?

Решение

По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:

Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.

Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».

Ускорение свободного падения

Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.

Сила тяжести — сила, с которой Земля притягивает все тела.

Сила тяжести

F — сила тяжести [Н]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

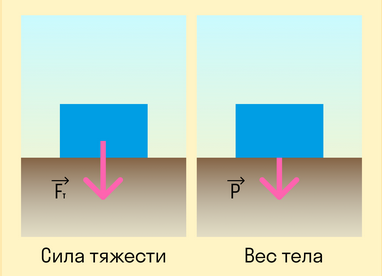
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.

Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.

На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.

Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:

Приравниваем правые части:

Делим на массу левую и правую части:

Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.

Закон всемирного тяготения

g — ускорение свободного падения [м/с 2 ]

M — масса планеты [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.

Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.

Но разве это не зависит еще и от массы предмета?

Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.

Третий закон Ньютона

Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.

Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще — сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈

Третий закон Ньютона

F₁ — сила, с которой первое тело действует на второе [Н]

F₂ — сила, с которой второе тело действует на первое [Н]

Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.

Задачка для практики

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?

Решение

Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.

Ответ: мяч притягивает Землю с силой 5 Н.

Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.

Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Закон всемирного тяготения. Движение тел под действием силы тяжести

Исходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.

Закон всемирного тяготения. Формулы

Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.

При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.

Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.

Ускорение свободного падения

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.

Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все объясняется законом тяготения и динамики.

Проявлении силы тяготения характеризуется наличием силы тяжести. Так называется сила притяжения тел к Земле и вблизи ее поверхности.

Когда М обозначается как масса Земли, R З – радиус, m – масса тела, то формула силы тяжести принимает вид:

Земля-Луна подходит в качестве примера взаимодействия системы двух тел.

Такая слабая гравитация характерна для космонавтов, находящихся на Луне. Поэтому можно совершать огромные прыжки и шаги. Прыжок вверх на метр на Земле соответствует семиметровому на Луне.

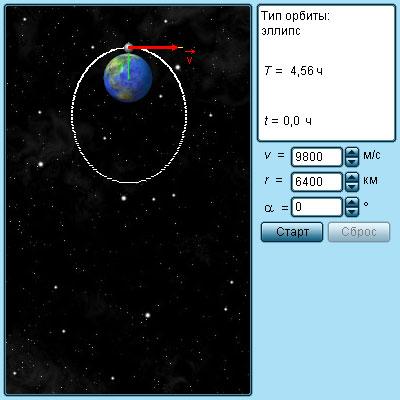
Искусственные спутники Земли

Применив кинематическую формулу для центростремительного ускорения, получаем

Но период обращения спутника по круговой орбите вблизи Земли намного больше, чем указано выше, так как существует различие между радиусом реальной орбиты и радиусом Земли.

Спутник движется по принципу свободного падения, отдаленно похожее на траекторию снаряда или баллистической ракеты. Разница заключается в большой скорости спутника, причем радиус кривизны его траектории достигает длины радиуса Земли.

Спутники, которые движутся по круговым траекториям на больших расстояниях, имеют ослабленное земное притяжение, обратно пропорциональное квадрату радиуса r траектории. Тогда нахождение скорости спутника следует по условию:

Поэтому, наличие спутников на высоких орбитах говорит о меньшей скорости их движения, чем с околоземной орбиты. Формула периода обращения равняется:

Источник

Сила тяготения.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: силы в механике, закон всемирного тяготения, сила тяжести, ускорение свободного падения, вес тела, невесомость, искусственные спутники Земли.

Закон всемирного тяготения.

Гравитационное взаимодействие любых двух тел во Вселенной подчиняется достаточно простому закону.

Закон всемирного тяготения. Две материальные точки массами и притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

Коэффициент пропорциональности называется гравитационной постоянной. Это фундаментальная константа, и её численное значение было определено на основе эксперимента Генри Кавендиша:

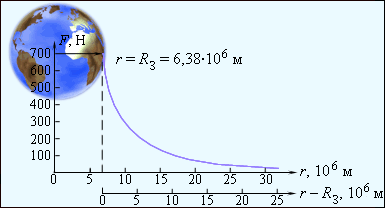
Порядок величины гравитационной постоянной объясняет, почему мы не замечаем взаимного притяжения окружающих нас предметов: гравитационные силы оказываются слишком малыми при небольших массах тел. Мы наблюдаем лишь притяжение предметов к Земле, масса которой примерно кг.

Второй случай особенно важен, так как позволяет применять формулу (1) для силы притяжения тела (например, искусственного спутника) к планете.

Сила тяжести.

Если тело находится на высоте над поверхностью планеты, то для силы тяжести получаем:

В последнем равенстве мы воспользовались соотношением

Вес тела. Невесомость.

Рис. 1. Сила тяжести, реакция опоры и вес тела

Предположим, что тело покоится. Тогда равнодействующая сил, приложенных к телу, равна нулю. Имеем:

Решение. Направим ось вертикально вверх (рис. 2 ).

Рис. 2. Вес тела больше силы тяжести.

Запишем второй закон Ньютона:

Перейдём к проекциям на ось :

Как видим, вес тела больше силы тяжести. Такое состояние называется перегрузкой.

Решение. Направим ось вертикально вниз (рис. 3 ).

Рис. 3. Вес тела меньше силы тяжести.

Схема решения та же. Начинаем со второго закона Ньютона:

Переходим к проекциям на ось :

Отсюда c. Следовательно, вес тела

Искусственные спутники.

Рис. 4. Спутник на круговой орбите.

Отсюда получаем выражение для скорости:

Источник

Для каких тел применим закон всемирного тяготения

1. Что было названо всемирным тяготением?

Силы притяжения, действующие между всеми телами во Вселенной, назвали всемирным тяготением.

2. Как иначе называются силы всемирного тяготения?

Силы всемирного тяготения иначе называют гравитационными силами.

3. Кто и в каком веке открыл закон всемирного тяготения?

В 1667 г. Исаак Ньютон в результате изучения движения Луны вокруг Земли и планет вокруг Солнца высказал предположение, что вообще между всеми телами действуют силы взаимного притяжения.

Исаак Ньютон сумел найти закон взаимодействия тел, т. е. формулу для расчёта гравитационной силы между двумя телами.

4. Как формулируется закон всемирного тяготения? Запишите формулу, выражающую этот закон.

Закон всемирного тяготения гласит:

Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.

Гравитационная постоянная численно равна силе F притяжения двух тел массой по 1 кг, находящихся на расстоянии 1 м друг от друга.

5. Почему мы замечаем силу притяжения всех тел к Земле, но не замечаем взаимного притяжения между самими этими телами?

5. Каковы границы применимости закона всемирного тяготения?
или
В каких случаях следует применять закон всемирного тяготения для расчёта гравитационных сил?

Формула для расчёта сил всемирного тяготения справедлива в трёх случаях:

1) если размеры тел пренебрежимо малы по сравнению с расстоянием между ними;

2) если оба тела однородны и имеют шарообразную форму;

7. Что надо понимать под расстоянием между телами в формуле закона всемирного тяготения?

Формула, выражающая закон всемирного тяготения, справедлива, когда расстояние между телами настолько велико по сравнению с их размерами, что тела можно считать материальными точками.
Направлена сила вдоль прямой, соединяющей эти материальные точки.

Материальными точками можно считать планеты и Солнце, Землю, Луну, когда вычисляют силы тяготения между ними.

Материальной точкой можно считать и тело произвольной формы, когда оно взаимодействует с шаром, радиус которого много больше размеров тела.
Именно так мы поступаем, когда рассматриваем притяжение тел к земному шару.

8. Можно ли по формуле закона всемирного тяготения рассчитать силу притяжения к Земле любого из находящихся на ней тел?

В качестве расстояния между телами следует брать радиус Земли, поскольку размеры всех тел, находящихся на ее поверхности или вблизи неё, пренебрежимо малы по сравнению с земным радиусом.

Силу притяжения тела к Земле называют также силой тяжести.

То есть силу тяжести можно рассчитывать и по формуле Fт = mg, и по формуле закона всемирного тяготения, взяв в формуле всемирного тяготения R равным радиусу Земли.

Тогда и ускорение тела, сообщаемое ему силой тяжести,- это и есть ускорение свободного падения g, которое равно:

9. Притягивается ли Земля к висящему на ветке яблоку?

По третьему закону Ньютона яблоко, висящее на ветке или падающее с неё с ускорением свободного падения, притягивает к себе Землю с такой же по модулю силой, с какой его притягивает Земля.
Но ускорение Земли, вызванное силой её притяжения к яблоку, близко к нулю, поскольку масса Земли несоизмеримо больше массы яблока.

Источник