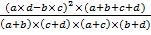для каких явлений характерна корреляционная связь
Понятие корреляционной связи



Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академические достижения, или связана ли продолжительность работы учителя в школе с размером его заработной платы, или с чем больше связан уровень умственного развития учащихся – с их успеваемостью по математике или по литературе и т.п.?
Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь – это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.
Корреляционные связи – это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статистики. «Оба термина, корреляционная связь и корреляционная зависимость – часто используются как синонимы. Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.
Корреляционная зависимость – это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.
Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Корреляционные связи различаютсяпо форме, направлению и степени (силе).
По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи. При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности.
Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.
Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
Максимальное возможное абсолютное значение коэффициента корреляции r=1,00; минимальное r=0,00.
Общая классификация корреляционных связей:
сильная, или тесная при коэффициенте корреляции r>0,70;
Корреляционная связь



Современная наука исходит из взаимосвязи всех явлений природы и общества. Объем продукции предприятия связан с численностью работников, мощностью двигателей, стоимостью производственных фондов и еще многими признаками.
Невозможно управлять явлениями, предсказывать их развитие без изучения характера, силы и других особенностей связей. Поэтому методы исследования составляют чрезвычайно важную часть методологии научного исследования, в том числе и статистического.
Различают два типа связей между различными явлениями и их признаками: функциональная или жестко детерминированную, с одной стороны, и корреляционная или стохастически детерминированную – с другой.
Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональная.
Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более. В реальной природе (и тем более в обществе) таких связей не существует; они являются лишь абстракциями, полезными и необходимыми при анализе явлений, но упрощающими реальность. Функциональная зависимость данной величины y от многих факторов x1, x2, …,xk возможна лишь только в том случае, если величина y зависит только от перечисленного набора факторов x1, x2, …,xk и не от чего более. Между тем все процессы и явления безграничного реального мира связаны между собой, и нет такого конечного числа переменных k, которые абсолютно полно определяли бы собой зависимую величину y. Следовательно, множественная функциональная зависимость переменных есть также абстракция, упрощающая реальность.
Однако такие науки, как механика, электротехника, акустика, политическая экономия и другие, успешно используют представление связей как функциональных не только в аналитических целях, но нередко и в целях прогнозирования. Это возможно потому, что в простых системах интересующая нас переменная величина зависит в основном от немногих других переменных или только от одной переменной. То есть связь в такой несложной системе является хотя и не абсолютно функциональной, но практически очень близкой к таковой.
Стахостическая детерминированная связь не имеет ограничений и условий, присущих функциональной связи. Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону – связь является корреляционная. Иными словами, при такой связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.
В настоящее время наука не знает более широкого определения связи. Все связи, которые могут быть измерены и выражены численно, подходят под определение «статистические связи», в том числе и функциональные.
Корреляционной связью называется важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные значения другой. С изменением значения признака х закономерным образом изменяется среднее значение признака у; в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.
Если же с изменением значения признака х среднее значение признака у не изменяется законным образом, но закономерно изменяется другая статистическая характеристика, то связь является корреляционной, хотя и статистической.
Корреляционная связь между признаками может возникать следующими путями:
1. Причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, признак х – бал оценки плодородия почв, признак у – урожайность сельскохозяйственной культуры.
2. Связь между двумя следствиями общей причины. Если в качестве признака х взять число пожарных команд в городе, а за признак у – сумму убытков за год в городе от пожаров, то между признаками х и у в совокупности городов России существенна прямая корреляция; в среднем, чем больше пожарников в городе, тем больше и убытков от пожаров. Но данную корреляцию нельзя интерпретировать как связь причины и следствия; оба признака – следствия – размера города.
3. Взаимосвязь признаков, каждый из которых и причина, и следствие. Например, корреляция между уровнями производительности труда рабочих и тарифной ставкой. С одной стороны, уровень зарплаты – следствие производительности труда. Но с другой стороны, установленные тарифные ставки и расценки играют стимулирующую роль. В такой системе признаков допустимы обе постановки задачи; каждый признак может выступать и в роли независимой переменной х, и в качестве зависимой переменной у.
Корреляционная связь, ее признаки, виды. Коэффициент корреляции, определение, свойства, методы вычисления. Метод корреляции рядов Пирсона. Метод корреляции рангов Спирмена.
Многие явления в медицине, так же как в природе и обществе, взаимосвязаны между собой. При проведении статистического исследования часто возникает необходимость проанализировать выявленные связи между различными явлениями и дать обобщающую характеристику. Различают 2 формы проявления связей между явлениями: функциональную и корреляционную.
Функциональная связь означает строгую зависимость одного признака от другого, когда определенному значению одной величины соответствует строго определенное значение другой. Например, радиусу круга соответствует определенная площадь круга; скорость свободно падающего тела определяется величиной ускорения, силой тяжести и временем падения. Функциональная связь характерна для физико-химических процессов.
Корреляционная связь — это такая связь, когда одной и той же величине одного признака соответствует несколько значений другого взаимосвязанного с ним признака. Врачи и биологи хорошо знакомы с этим видом связи: при одинаковой температуре у различных людей наблюдаются индивидуальные колебания частоты пульса; при одинаковом росте отмечаются различные колебания масс тела.
По форме корреляционная связь:
Прямолинейная связь — равномерные изменения одного признака соответствуют равномерным изменениям второго признака при незначительных отклонениях.
Криволинейная связь — равномерные изменения одного признака, соответствуют неравномерным изменениям второго признака, причем неравномерность имеет определенную закономерность. Общая тенденция в определенном моменте изменяет свос направление, дает изгиб.
Направление связи:
Прямая связь (положительная) — если с увеличением одного признака второй также увеличивается или с уменьшением одного признака другой тоже уменьшается. Обратная связь (отрицательная) — когда с увеличением одного признака, другой, корреляционно связанный с ним признак, уменьшается.
Под силой связи следует понимать степень корреляции (степень сопряженности между признаками).
Измерение силы связи и определение ее направления осуществляется путем вычисления коэффициента корреляции. Существуют следующие методы вычисления коэффициента корреляции: рядов, рангов, путем составления корреляционной решетки.
Коэффициент корреляции рядов (rxy) (Пирсона):
rxy = 
Для оценки достоверности коэффициента корреляции вычисляется средняя ошибка коэффициента корреляции:
mr = 
mr = 
mr = 
Для оценки величины полученной ошибки следует использовать критерий достоверности (t).
t =
Значение критерия (t) оценивается по специальной таблице Стьюдента. Если полученное значение t больше табличного для выбранного уровня доверия и числа степеней свободы, то коэффициент корреляции считается достоверным.
Коэффициент корреляции рангов ( 
Коэффициент корреляции рангов относится к непарамегрическим критериям. Он используется при необходимости получения быстрого результата, при малом числе наблюдений, а также в тех случаях, когда изучаемые признаки не имеют точных количественных значений или носят описательный характер. Этот метод основан на определении ранга (места) каждого из значений ряда.


Вычисления проводятся по следующему алгоритму:
1) Определить ранги по значению каждой величины ряда. (1,2,3,4…) Если первый ряд (x) ранжируется от меньшего значения к большему, то второй ряд (у) следует ранжировать в том же порядке.
3) Возвести в квадрат полученные разности и суммировать их.
4) Рассчитать коэффициент корреляции рангов по формуле.
Прежде чем судить о степени связи между изучаемыми признаками, необходимо оценить достоверность коэффициента корреляции рангов.
t =
Полученное значение критерия t оценивается по таблице t-критерия Стьюдента для числа степеней свободы n’ = n-2. Коэффициент корреляции незначим, если рассчитанное значение меньше табличного.
Понятие о непараметрических методах исследования. Критерий соответствия (χ-квадрат), этапы расчета, значение. Понятие о нулевой гипотезе.
Одной из важнейших задач применения математико-статистических методов является оценка достоверности полученных результатов при исследовании и определении наличия связи между какими-либо изучаемыми факторами. Этой задаче отвечает критерий хи-квадрат – коэффициент соответствия или коэффициента согласия.
Как известно, оценка достоверности различий может производиться путем вычисления критерия t (критерия Стьюдента). Однако, он рассматривает различия только между двумя статистическими совокупностями. При сравнении трех и более статистических групп оценка достоверности при помощи критерия t затруднительна, так как попарное сравнение не дает общей оценки. Кроме того, сравниваемые группы имеют не два результата (да, нет), а несколько.
Критерий соответствия используется для:
– оценки различия в двух или более сравниваемых статистических группахи при нескольких результатах с определенной степенью достоверности. Например, 4 группы больных у которых применимы различные методы лечения; несколько учреждений (отделений) с разными показателями деятельности, легальности; разные группы больных, имеющие разный процент осложнений;
– определения наличия связи между двумя факторами (результат и зависимый признак). Например, зависимость результатов лечения от степени тяжести заболевания, возраста, медико-гигиенических характеристик. Связь между жилищными условиями, материальным обеспечением семьи и т.д. и частотой заболеваний, госпитализаций.
– рассмотрения идентичности распределений частот в двух и более вариационных рядах. Например, одинаково ли распределение больных по содержанию гемоглобина, количеству эритроцитов, белков крови в двух статистических совокупностях (две группы больных с разными заболеваниями, различной степенью тяжести и т.д.)
Применение метода «хи-квадрат» основано на использовании абсолютных значений, представляющих собою распределение признака в совокупности, но не на средних величинах.
Критерий соответствия χ 2 вычисляется из абсолютных величин и указывает на существенную или несущественную разницу между «фактическими» числами, полученными в процессе исследования, и теоретическими, «ожидаемыми», полученными на основе предположения об отсутствии связи между исследуемыми явлениями, т.е. на основе принятия нулевой гипотезы. Хи-квадрат подтверждает наличие связи, но не устанавливает степень связи. Чем больше величина хи-квадрат, тем больше полученный результат отличается от теоретического.
Сущность метода «хи-квадрат» заключается в определении достоверности отклонений наблюдаемых фактических и теоретических («ожидаемых») данных, получениых при условии отсутствия различия в сравниваемых группах
χ 2 = ∑
Оценка полученного значения хи-квадрата производится по специальной таблице. Если значение хи-квадрат больше или равно табличному, то нулевая гипотеза отвергается, чем доказывается связь или влияние изучаемого фактора.
Методика вычисления: (на примере)
1) Приводим фактические данные, из которых следует, чем позднее сделана операция, тем выше будет послеоперационная летальность.
2) Принимаем «нулевую гипотезу». Теоретически предполагаем, что сроки операции от момента госпитализации больных не влияют на частоту летальных исходов и показатель летальности одинаков во все сроки от момента госпитализации больных
3) Вычисляем «ожидаемые» (P1) данные в соответствия с «нулевой» гипотезой, т.е. «ожидаемые числа» умерших и выздоровевших среди оперированных.
Табличный «хи-квадрат» определяем по числу «степеней свободы», которое равно произведению числа граф, без итоговой, минус единица на число строк без итоговой, минус единица:
Полученное значение χ 2 намного больше чисел стоящих в строке n´, следовательно нулевая гипотеза отвергается, что позволяет сделать вывод о влиянии на уровни послеоперационной летальности при остром аппендиците сроков операции от момента госпитализации больных.
Можно упростить вычисление показателя χ 2 (альтернативная вариация), использовав формулу, пригодную для «четырехпольной таблицы». Клетки таблицы условно обозначаются буквами.
χ 2 =
Для каких явлений характерна корреляционная связь
Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
при наличии вычислительной техники расчет производится по формуле:
Способ 1
Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n — 2), где n — число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.
Способ 2
Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n — 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.
на применение метода квадратов
Задание: вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) |
| 4 8 11 27 34 37 | 28 56 77 191 241 262 |
Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.
Решение.
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.
Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: rху = + 0,99, р > 99,9%).
на применение рангового метода
Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:
| Стаж работы в годах | Число травм на 100 работающих |
| до 1 года 1-2 3-4 5-6 7 и более | 24 16 12 12 6 |
Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака «стаж работы в годах» имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод — метод квадратов.
Решение. Последовательность расчетов изложена в тексте, результаты представлены в табл. 2.
где n — число сопоставляемых пар вариант в ряду «x» и в ряду «у»
1-й способ. Определить ошибку (mрху) коэффициента ранговой корреляции и оценить достоверность его с помощью критерия t:
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)
| Число степеней свободы — 2 | Уровень вероятности р (%) | ||
| 95% | 98% | 99% | |
| 1 | 0,997 | 0,999 | 0,999 |
| 2 | 0,950 | 0,980 | 0,990 |
| 3 | 0,878 | 0,934 | 0,959 |
| 4 | 0,811 | 0,882 | 0,917 |
| 5 | 0,754 | 0,833 | 0,874 |
| 6 | 0,707 | 0,789 | 0,834 |
| 7 | 0,666 | 0,750 | 0,798 |
| 8 | 0,632 | 0,716 | 0,765 |
| 9 | 0,602 | 0,885 | 0,735 |
| 10 | 0,576 | 0,858 | 0,708 |
| 11 | 0,553 | 0,634 | 0,684 |
| 12 | 0,532 | 0,612 | 0,661 |
| 13 | 0,514 | 0,592 | 0,641 |
| 14 | 0,497 | 0,574 | 0,623 |
| 15 | 0,482 | 0,558 | 0,606 |
| 16 | 0,468 | 0,542 | 0,590 |
| 17 | 0,456 | 0,528 | 0,575 |
| 18 | 0,444 | 0,516 | 0,561 |
| 19 | 0,433 | 0,503 | 0,549 |
| 20 | 0,423 | 0,492 | 0,537 |
| 25 | 0,381 | 0,445 | 0,487 |
| 30 | 0,349 | 0,409 | 0,449 |
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов