для какой цели используются криптографические ключи
СОДЕРЖАНИЕ
Сфера
Симметричная криптография
Асимметричная криптография
Асимметричная криптография имеет отдельные ключи для шифрования и дешифрования. Эти ключи известны как открытый и закрытый ключи соответственно.
Поскольку ключ защищает конфиденциальность и целостность системы, важно хранить его в секрете от посторонних лиц. При криптографии с открытым ключом в секрете должен храниться только закрытый ключ, но при симметричной криптографии важно сохранять конфиденциальность ключа. Принцип Керкхоффа гласит, что вся безопасность криптографической системы зависит от секретности ключа.
Ключевые размеры
Раньше ключи должны были иметь длину не менее 40 бит, однако по мере развития технологий эти ключи взламывались все быстрее и быстрее. В ответ ограничения на симметричные ключи были увеличены и стали больше по размеру.
Генерация ключей
Некоторые операционные системы включают инструменты для «сбора» энтропии по времени непредсказуемых операций, таких как движения головки дисковода. Для производства небольшого количества ключевого материала обычные игральные кости являются хорошим источником высококачественной случайности.
Схема учреждения
Подтверждение ключа обеспечивает уверенность между получателем подтверждения ключа и поставщиком в том, что материалы для совместного использования ключей верны и установлены. Национальный институт стандартов и технологии рекомендуют ключ подтверждения для интеграции в ключевую схему установления для проверки ее реализации.
Управление
Управление ключами касается генерации, создания, хранения, использования и замены криптографических ключей. Система управления ключами (KMS) обычно включает три этапа: создание, хранение и использование ключей. Основа безопасности для генерации, хранения, распространения, использования и уничтожения ключей зависит от успешных протоколов управления ключами.
Ключ против пароля
Пароль менее безопасен, чем криптографический ключ, из-за его низкой энтропии, случайности и удобочитаемых свойств. Однако пароль может быть единственными секретными данными, доступными криптографическому алгоритму для защиты информации в некоторых приложениях, таких как защита информации в устройствах хранения. Таким образом, детерминированный алгоритм, называемый функцией деривации ключа (KDF), использует пароль для генерации защищенного материала криптографического ключа, чтобы компенсировать слабость пароля. При генерации могут использоваться различные методы, такие как добавление соли или растяжение ключа.
Криптографические ключи, адреса, кошельки
Почему это важно?
Цель: Сформировать понимание важности криптографических алгоритмов для криптовалют.
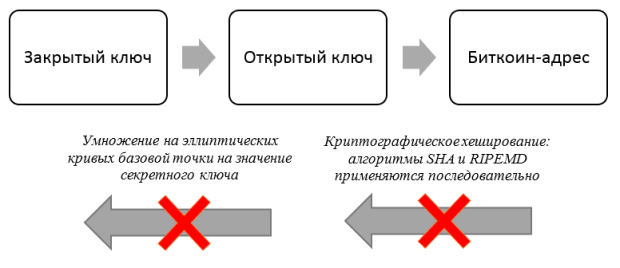
Право владения токенами, в том числе, биткоинами устанавливается через криптографические (цифровые) ключи, Биткоин-адреса и цифровые подписи. Закрытые криптографические ключи не перемещаются по сети. Они генерируются и хранятся пользователями в специализированном клиенте (кошельке). Цифровые ключи в кошельке пользователя являются абсолютно независимыми от протокола Биткоин, генерируются и управляются с помощью программного обеспечения кошелька пользователя без обращений к блокчейну или к сети Интернет. Благодаря такой стратегии управления ключами становятся возможными многие из важнейших свойств сети Биткоин, в том числе децентрализованные консенсус и контроль, подтверждение владения, и модель безопасности, основанная на математическом (криптографическом) доказательстве.
Каждая транзакция в сети Биткоин должна быть подписана подлинной электронной подписью, которая может быть получена только при наличии валидных цифровых криптографических ключей. Следовательно, любой, получивший копии данных ключей, имеет точно такой же контроль над средствами, ассоциированными с этой учетной записью, как и ее истинный владелец.
Ассиметричная схема шифрования подразумевает наличие криптопары: частного (закрытого) и публичного (открытого) ключей. Публичный ключ можно сравнить с номером банковского счета, тогда приватный ключ выполняет функцию PIN-кода или подписи на банковском чеке, обеспечивая полный доступ к учетной записи. Эти цифровые ключи почти никогда не попадаются на глаза пользователям сети Биткоин. В основном, они хранятся в файлах бумажника, а манипуляции ключами выполняет программное обеспечение кошелька – разумеется по инициативе владельца.
Если рассматривать процедуру платежа, то в соответствующей транзакции фигурирует Биткоин-адрес получателя, являющийся фактически цифровым отпечатком открытого ключа. Сравним его с именем получателя денежных средств на банковском чеке.
В большинстве случаев биткоин-адрес формируется на основе публичного ключа. По крайней мере, это утверждение справедливо в отношении всех обладателей собственных аккаунтов. Забегая вперед скажем, что получателями средств могут быть сценарии. Их биткоин-адреса определяются по иной схеме.
Таким образом, в рамках сети Биткоин адреса обеспечивают анонимность пользователей. Не существует способа ассоциировать биткоин-адрес с конкретным физическим или юридическим лицом. Но эта анонимность поддерживается только в рамках сети Биткоин. Использование токенов на криптобиржах или магазинах, принимающих криптовалюту, в большинстве случае потребует стандартной идентификации владельца криптосредств. Из выше сказанного следует, что в отличие от стандартной схемы цифровой подписи даже публичный ключ не распространяется по сети и не передается другим пользователям. Вместо него для решения задач авторизации используются биткоин-адреса.
Криптография с открытым ключом
Цель: Определить «точки пересечения» ассиметричной криптографии и протокола Биткоин.
Криптография с открытым ключом была изобретена в 70-х годах прошлого века. Именно ассиметричные криптоалгоритмы традиционно стали использоваться в качестве математической основы при построении систем компьютерной и информационной безопасности. В процессе становления криптографии с открытым ключом было найдено несколько классов математических функций, получивших название односторонние. К ним, в частности, относятся возведение в степень простого числа, умножение эллиптических кривых и др. Необратимость означает, что прямые значения такого рода функций вычисляются достаточно просто, а вот обратные рассчитать практически невозможно. На основе односторонних функций разработано довольно много алгоритмов цифровых шифров и криптостойких электронных подписей.
В сети Биткоин для создания криптопары, контролирующей доступ к счету, используется умножение на эллиптических кривых. Так же, как и в других ассиметричных криптосистемах пара ключей состоит из закрытого ключа и производного от него, уникального открытого ключа. Публичный и приватный ключи однозначно связаны математическим соотношением. Такая связь обеспечивает возможность подписи сообщения приватным ключом с одной стороны, и последующую проверку правильности подписи при помощи публичного ключа, с другой. При этом приватный ключ не раскрывается. В платежных операциях открытый ключ используется для получения биткоинов (как основание для определения адреса), а с помощью закрытого ключа подписываются транзакции, предназначенные для траты имеющихся на балансе счета средств (на самом деле понятие баланса в привычном понимании в сети Биткойн не применяется). Фактически, любой пользователь, намереваясь потратить имеющиеся у него биткоины, должен опубликовать в сети свои открытый ключ и электронную подпись транзакции, полученную с помощью соответствующего закрытого ключа. После публикации этих данных любой участник сети (и, в первую очередь, майнеры) могут проверить правомочность совершаемых финансовых действий и признать транзакцию действительной. Сделка будет считаться совершенной после того как проверенная транзакция в составе очередного валидного блока будет включена в блокчейн.
Поскольку открытый ключ в любой момент может быть вычислен на основе закрытого ключа, некоторые кошельки хранят только приватные ключи.
Управление ключами в сети Биткоин
Цель: Сформировать понимания процессов преобразования цепочки криптографических преобразований: Закрытый ключ → Открытый ключ → Биткоин-адрес.
Связь между криптопарой (закрытым и открытым ключами) и биткоин-адресом продемонстрирована на рисунке 2.1.
Рассмотрим эти вопросы подробнее.
Закрытые ключи
Цель: Сформировать четкое понимание процесса и развить практические навыки получения закрытых ключей в сети Биткоин.
Закрытый ключ — это просто число, взятое наугад. Только владелец закрытого ключа контролирует средства, связанные с определенным биткоин-адресом.
Секретный ключ используется для создания электронной подписи, необходимой в качестве неопровержимого доказательства права владения средствами в транзакции. Секретный ключ должен храниться в строжайшем секрете. Его несанкционированное копирование по сути означает передачу контроля над средствами в чужие руки.
Следует позаботиться о создании резервной копии секретного ключа. В случае его потери доступ к соответствующим средствам также будет утрачен. Они окажутся замороженными в блокчейне сети Биткоин навсегда. Не существует никакого легального способа ими воспользоваться. Ни у кого в целом мире, включая Сатоши Накомото.
Задача осложняется тем, что большинство привычных инструментов генерации случайных чисел выдают, так называемые, псевдослучайные последовательности, не основанные на надежных источниках энтропии. Самый надежный способ состоит в использовании квантовых генераторов случайных бинарных последовательностей, примеры практической реализации которых уже известны. Основаны такие устройства на принципиально ином источнике случайности, чем большинство традиционных генераторов. А именно, квантовой неопределенности. Согласно фундаментальным законам квантовой механики, у электрона или другой частицы нет траектории, которую можно проследить. Есть лишь вероятность обнаружить частицу в той или иной области пространства. И подобную энтропию невозможно устранить даже теоретически. На самом деле такая неопределенность характерна не только для движения элементарных частиц, но и присуща, по сути, всем квантовым процессам. В обозримом будущем, наверняка, именно такие генераторы существенно снимут остроту проблемы. Но пока на практике прибегают к более предсказуемым, а потому ненадежным инструментам генерации случайных чисел.
Ниже приведен случайным образом сгенерированный секретный ключ (k) в шестнадцатеричном формате (64 шестнадцатеричных цифры):
Отображение секретного ключа в виде числовой последовательности не всегда является удобным. Часто прибегают к более прогрессивному формату WIF (Wallet Import Format). Значение в таком формате получается довольно просто. Двоичную запись ключа предваряют специальным префиксом – числом 128 ( 0x80 в шестнадцатеричной системе счисления). Полученное значение записывают в формате Base58Check. О кодировке Base58Check чуть позже мы поговорим подробнее. Пока представим пример записи секретного ключа в формате WIF:
Открытые ключи
Цель: Сформировать четкое понимание процесса получения открытых ключей в сети Биткоин.
Открытый ключ K получается из секретного путем одностороннего скалярного умножения на эллиптических кривых базовой точки на значение секретного ключа.
где k — это приватный ключ, G — базовая точка,
Криптография на эллиптических кривых
Криптография на эллиптических кривых — это вид асимметричной криптографии или криптографии с открытым ключом, основанная на проблеме дискретного логарифмирования на эллиптических кривых.
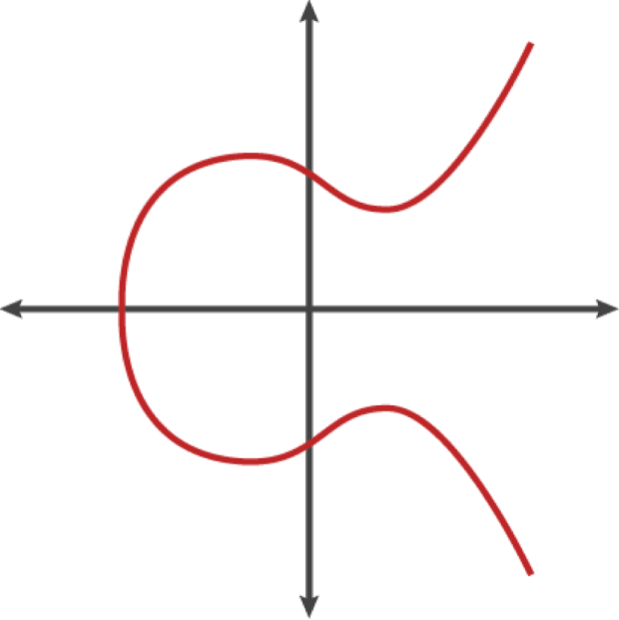
На рисунке 6 продемонстрирован пример эллиптической кривой, аналогичной той, которая используется в платформе Биткоин.
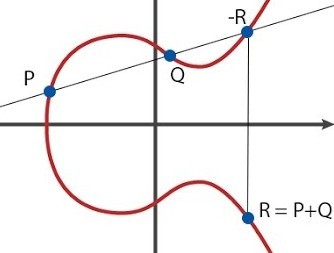
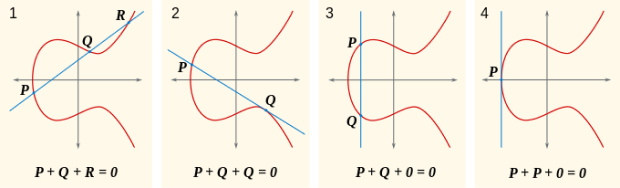
Эллиптические кривые обладают целым набором полезных свойств. Например, любая наклонная прямая, пересекающая эллиптическую кривую в двух точках, всегда будет пересекать ее также в третьей точке. Следующим фактом является то, что любая наклонная прямая, являющаяся касательной к кривой в одной из точек, обязательно пересечет кривую еще ровно в одной точке. Эти свойства окажутся востребованными в криптосистемах.
В сети Биткоин используется конкретная эллиптическая кривая и набор математических констант из стандарта под названием secp256k1 установленного Национальным Институтом Стандартов и Технологий (NIST).
Уравнение эллиптической кривой: y 2 = x 3 + 7
Определенной над полем y 2 mod p = x 3 + 7 (mod p)
Х = 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
Y = 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
В ECDSA секретный ключ — это случайное число между единицей и значением порядка.
Открытый ключ = секретный ключ · значение базовой точки.
Постараемся в этом разобраться подробнее.
Для коэффициентов a = 0 и b = 7 (используемых в платформе Биткоин), график функции изображен на рисунке 2.2.
В эллиптической криптографии используется такая же кривая, но определенная над некоторым конечным полем.
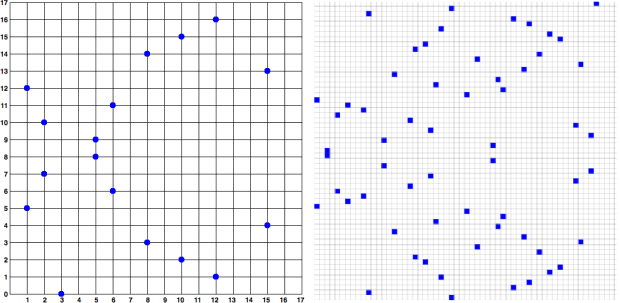
Поскольку эллиптическая кривая определена над конечным полем простого порядка, а не вещественных чисел, она выглядит как узор из точек, рассеянных в двух измерениях, что достаточно трудно визуализировать. Тем не менее, математика идентична математике эллиптической кривой в вещественных числах. В качестве примера, на рисунке 2.3 отображены эллиптические кривые над полем очень скромных конечных простых порядков ( р = 17, р = 59 ), иллюстрирующая то, каким образом располагаются точки на координатной сетке. Эллиптическая кривая, используемая в криптосистеме платформы Биткоин, secp256k1 представляет собой гораздо более сложную совокупность точек, распределенных на неизмеримо большей координатной сетке.
при р = 17 и при р = 59
Эллиптическая кривая на множестве вещественных чисел (непрерывные числовые значения, в том числе и дробные) не позволяет получить однозначное соответствие (биекцию) исходных данных их образам (хешам). Чтобы не усложнять, и без того не простые, расчетные методы еще и округлением, для целей криптографии используются только точки с координатами из множества конечных полей. Исходя из этого, на эллиптической кривой берутся точки со значениями координат попадающими в конечное поле.
Вспомним основные свойства эллиптических кривых. И постараемся понять, как их можно использовать в криптографии.
Эллиптическая кривая над полем есть неособая кубическая кривая на проективной плоскости над алгебраическим замыканием поля, задаваемая уравнением 3-й степени с коэффициентами из поля и «точкой на бесконечности»
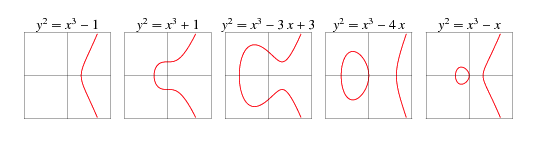
В зависимости от значений параметров a и b график данной функции может выглядеть по-разному:
Математики давно заинтересовались эллиптическими кривыми. Первые упоминания о них находят в трудах Диофанта. А в 17 веке, ее свойства исследовал Ньютон. Именно его труды послужили основой для формализации правил сложения точек на эллиптической кривой.
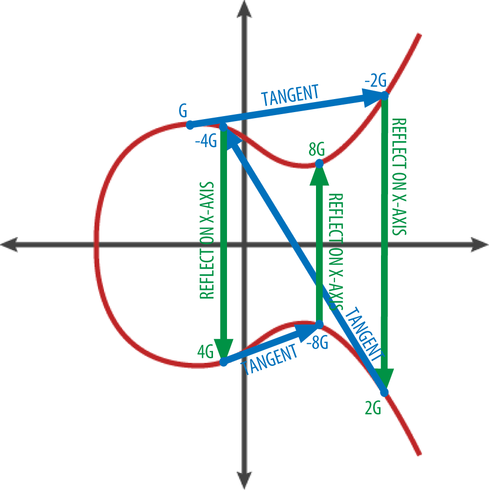
Таким образом, скалярное умножение на эллиптических кривых это тоже самое, что и суммирование точки G самой с собой k раз подряд. В свою очередь, каждое «удвоение» точки G является эквивалентом построения касательной к упомянутой точке, нахождения пересечения построенной прямой с эллиптической кривой и отображения найденной точки пересечения относительно оси абсцисс.
Создание открытого ключа
Цель: Сформировать практические навыки получения открытых ключей в сети Биткоин.
Введение в криптографию и шифрование, часть первая. Лекция в Яндексе
Чтобы сходу понимать материалы об инфраструктуре открытых ключей, сетевой безопасности и HTTPS, нужно знать основы криптографической теории. Один из самых быстрых способов изучить их — посмотреть или прочитать лекцию Владимира ivlad Иванова. Владимир — известный специалист по сетям и системам их защиты. Он долгое время работал в Яндексе, был одним из руководителей нашего департамента эксплуатации.
Мы впервые публикуем эту лекцию вместе с расшифровкой. Начнём с первой части. Под катом вы найдёте текст и часть слайдов.
Я когда-то читал в МГУ лекции по крипте, и они занимали у меня по полгода. Я попытаюсь вам всё рассказать за два с половиной часа. Никогда этого не делал. Вот и попробуем.
Кто понимает, что такое DES? AES? TLS? Биноминальное отображение?
Говорить постараемся в общих терминах, потому что сложно и глубоко разбирать не получится: мало времени и базовая подготовка должна быть довольно большой. Будем оперировать общими концепциями, довольно поверхностно.
Мы поговорим о том, что такое криптографические примитивы, простые штучки, из которых впоследствии можно строить более сложные вещи, протоколы.
Мы будем говорить о трех примитивах: симметричном шифровании, аутентификации сообщений и асимметричном шифровании. Из них вырастает очень много протоколов.
Сегодня мы попробуем чуть-чуть поговорить про то, как вырабатываются ключи. В общем виде поговорим о том, как отправить защищенное сообщение, используя криптопримитивы, которые у нас есть, от одного пользователя другому.
Когда люди говорят про крипту вообще, есть несколько фундаментальных принципов. Один из них — принцип Керкгоффса, который говорит, что open source в криптографии очень важен. Если точнее, он дает общее знание об устройстве протоколов. Смысл очень простой: криптографические алгоритмы, которые используются в той или иной системе, не должны быть секретом, обеспечивающим ее устойчивость. В идеале необходимо строить системы так, чтобы их криптографическая сторона была полностью известна атакующему и единственным секретом являлся криптографический ключ, который в данной системе используется.
Современные и коммерчески доступные системы шифрования — все или почти все или лучшие из них — построены из компонент, устройство и принцип работы которых хорошо известны. Единственная секретная вещь в них — ключ шифрования. Есть только одно известное мне значимое исключение — набор секретных криптографических протоколов для всевозможных государственных организаций. В США это называется NSA suite B, а в России это всякие странные секретные алгоритмы шифрования, которые до определенной степени используются военными и государственными органами.
Не сказал бы, что такие алгоритмы приносят им большую пользу, за исключением того, что это примерно как атомная физика. Можно попытаться по пониманию дизайна протокола понять направление мысли людей, которые его разработали, и неким образом обогнать другую сторону. Не знаю, насколько такой принцип актуален по нынешним меркам, но люди, знающие про это больше меня, поступают именно так.
В каждом коммерческом протоколе, с которым вы столкнетесь, ситуация обстоит иначе. Там везде используется открытая система, все придерживаются этого принципа.
Первый криптографический примитив — симметричные шифры. 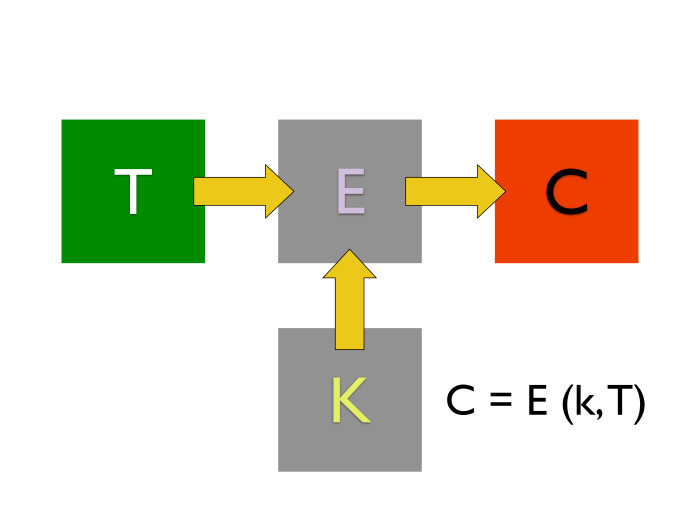
Они очень простые. У нас есть какой-то алгоритм, на вход которого поступает открытый текст и нечто, называемое ключом, какое-то значение. На выходе получается зашифрованное сообщение. Когда мы хотим его дешифровать, важно, чтобы мы брали тот же самый ключ шифрования. И, применяя его к другому алгоритму, алгоритму расшифровки, мы из шифротекста получаем наш открытый текст назад. 
Какие здесь важные нюансы? В большинстве распространенных алгоритмов симметричного шифрования, с которыми можно столкнуться, размер шифротекста всегда равен размеру открытого текста. Современные алгоритмы шифрования оперируют размерами ключей. Размер ключей измеряется в битах. Современный размер — от 128 до 256 бит для алгоритмов симметричного шифрования. Об остальном, в том числе о размере блока, мы поговорим позже. 
Исторически, в условном IV веке до нашей эры, существовало два метода дизайна шифров: шифры подстановки и перестановки. Шифры подстановки — алгоритм, где в те времена заменяли одну букву сообщения на другую по какому-то принципу. Простой шифр подстановки — по таблице: берем таблицу, где написано, что А меняем на Я, Б на Ю и т. д. Дальше по этой таблице шифруем, по ней же дешифруем.
Как вы считаете, с точки зрения размера ключа насколько это сложный алгоритм? Сколько вариантов ключей существует? Порядок факториала длины алфавита. Мы берем таблицу. Как мы ее строим? Допустим, есть таблица на 26 символов. Букву А можем заменить на любой из них, букву Б — на любой из оставшихся 25, С — на любой из оставшихся 24… Получаем 26*25*24*… — то есть факториал от 26. Факториал размерности алфавита.
Если взять log226!, это будет очень много. Думаю, вы точно получите в районе 100 бит длины ключа, а то и поболее. Оказалось, что с точки зрения формального представления стойкости указанный алгоритм шифрования — довольно неплохой. 100 бит — приемлемо. При этом все, наверное, в детстве или юности, когда сталкивались с кодировками, видели, что такие алгоритмы дешифруются тривиально. Проблем с расшифровкой нет.
Долго существовали всякие алгоритмы подстановки в разных конструкциях. Одним из них, еще более примитивным, является шифр Цезаря, где таблица формируется не случайной перестановкой символов, а сдвигом на три символа: А меняется на D, B на Е и т. д. Понятно, что шифр Цезаря вместе со всеми его вариантами перебрать очень легко: в отличие от табличной подстановки, в ключе Цезаря всего 25 вариантов при 26 буквах в алфавите — не считая тривиального шифрования самого в себя. И его как раз можно перебрать полным перебором. Здесь есть некоторая сложность.
Почему шифр табличной подстановки такой простой? Откуда возникает проблема, при которой мы можем легко, даже не зная ничего про криптографию, расшифровать табличную подстановку? Дело в частотном анализе. Есть самые распространенные буквы — какая-нибудь И или Е. Их распространенность велика, гласные встречаются намного чаще, чем согласные, и существуют негативные пары, никогда не встречающиеся в естественных языках, — что-то вроде ЬЪ. Я даже давал студентам задание сделать автоматический дешифратор шифра подстановки, и, в принципе, многие справлялись.
В чем проблема? Надо статистику распределения букв исказить, чтобы распространенные буквы не так светились в зашифрованном тексте. Очевидный способ: давайте будем шифровать самые часто встречающиеся буквы не в один символ, а в пять разных, например. Если буква встречается в среднем в пять раз чаще, то давайте по очереди — сначала в первый символ будем зашифровывать, потом во второй, в третий и т. д. Далее у нас получится маппинг букв не 1 к 1, а, условно, 26 к 50. Статистика, таким образом, нарушится. Перед нами первый пример полиалфавитного шифра, который как-то работал. Однако с ним есть довольно много проблем, а главное, очень неудобно работать с таблицей.
Дальше придумали: давайте не будем шифровать такими таблицами, а попробуем брать шифр Цезаря и для каждой следующей буквы изменять сдвиг. Результат — шифр Виженера.
Берем в качестве ключа слово ВАСЯ. Берем сообщение МАША. Задействуем шифр Цезаря, но отсчитывая от этих букв. Например, В — третья буква в алфавите. Мы должны сдвинуть на три буквы соответствующую букву в открытом тексте. М сдвигается в П. А в А. Ш — на 16, перескочим букву А, получим, условно, Д. Я сдвинет А в Я. ПАДЯ.
Что удобно в получившемся шифре? Здесь было две одинаковых буквы, но в результате они зашифровались в разные. Это классно, потому что размывает статистику. Метод хорошо работал, пока где-то в XIX веке, буквально недавно на фоне истории криптографии, не придумали, как его ломать. Если посмотреть на сообщение из нескольких десятков слов, а ключ довольно короткий, то вся конструкция выглядит как несколько шифров Цезаря. Мы говорим: окей, давайте каждую четвертую букву — первую, пятую, девятую — рассматривать как шифр Цезаря. И поищем среди них статистические закономерности. Мы обязательно их найдем. Потом возьмем вторую, шестую, десятую и так далее. Опять найдем. Тем самым мы восстановим ключ. Единственная проблема — понять, какой он длины. Это не очень сложно, ну какой он может быть длины? Ну 4, ну 10 символов. Перебрать 6 вариантов от 4 до 10 не очень сложно. Простая атака — она была доступна и без компьютеров, просто за счет ручки и листа бумаги.
Как из этой штуки сделать невзламываемый шифр? Взять ключ размера текста. Персонаж по имени Клод Шэннон в ХХ веке, в 1946 году, написал классическую первую работу по криптографии как по разделу математики, где сформулировал теорему. Длина ключа равна длине сообщения — он использовал XOR вместо сложения по модулю, равному длине алфавита, но в данной ситуации это не очень принципиально. Ключ сгенерирован случайным образом, является последовательностью случайных бит, и на выходе тоже получится случайная последовательность бит. Теорема: если у нас есть такой ключ, то подобная конструкция является абсолютно стойкой. Доказательство не очень сложное, но сейчас не буду про него говорить.
Важно, что можно создать невзламываемый шифр, но у него есть недостатки. Во-первых, ключ должен быть абсолютно случайным. Во-вторых, он никогда не должен использоваться повторно. В-третьих, длина ключа должна быть равна длине сообщения. Почему нельзя использовать один и тот же ключ для шифровки разных сообщений? Потому что, перехватив этот ключ в следующий раз, можно будет расшифровать все сообщения? Нет. В первых символах будет виден шифр Цезаря? Не очень понял. Кажется, нет.
Возьмем два сообщения: МАША, зашифрованная ключом ВАСЯ, и другое слово, у которого ключ тоже был ВАСЯ, — ВЕРА. Получим примерно следующее: ЗЕШЯ. Сложим два полученных сообщения, причем так, чтобы два ключа взаимно удалились. В итоге получим лишь разницу между осмысленным шифротекстом и осмысленным шифротекстом. На XOR это делается удобнее, чем на сложении по длине алфавита, но разницы практически никакой.
Если мы получили разницу между двумя осмысленными шифротекстами, то дальше, как правило, становится намного легче, поскольку у текстов на естественном языке высокая избыточность. Зачастую мы можем догадаться, что происходит, делая разные предположения, гипотезы. А главное, что каждая верная гипотеза будет раскрывать нам кусочек ключа, а значит и кусочки двух шифротекстов. Как-то так. Поэтому плохо.
Помимо шифров подстановки, были еще шифры перестановки. С ними тоже все довольно просто. Берем сообщение ВАСЯИ, записываем его в блок какой-то длины, например в ДИДОМ, и считываем результат так же.
Не бог весть какая штука. Как ее ломать, тоже понятно — переберем все возможные варианты перестановок. Тут их не очень много. Берем длину блока, подбираем и восстанавливаем.
В качестве следующей итерации был выбран такой способ: возьмем все то же самое, а сверху напишем какой-нибудь ключ — СИМОН. Переставим столбцы так, чтобы буквы оказались в алфавитном порядке. В итоге получим новую перестановку по ключу. Она уже намного лучше старой, поскольку количество перестановок намного больше и подобрать ее не всегда легко.
Каждый современный шифр тем или иным способом базируется на этих двух принципах — подстановки и перестановки. Сейчас их использование намного более сложное, но сами базовые принципы остались прежними. 
Если говорить про современные шифры, они делятся на две категории: поточные и блочные. Поточный шифр устроен так, что фактически представляет собой генератор случайных чисел, выход которого мы складываем по модулю 2, «ксорим», с нашим шифротекстом, как видно у меня на слайде. Ранее я сказал: если длина получившегося ключевого потока — она же ключ — абсолютно случайная, никогда повторно не используется и ее длина равна длине сообщения, то у нас получился абсолютно стойкий шифр, невзламываемый.
Возникает вопрос: как сгенерировать на такой шифр случайный, длинный и вечный Ключ? Как вообще работают поточные шифры? По сути, они представляют собой генератор случайного числа на основе какого-то начального значения. Начальное значение и является ключом шифра, ответом.
Из этой истории есть одно занятное исключение — шифроблокноты. Речь идет о настоящей шпионской истории про настоящий шпионаж. Некие люди, которым нужна абсолютно устойчивая коммуникация, генерируют случайные числа — например, буквальным бросанием кубика или буквальным выниманием шаров из барабана, как в лото. Создают два листа, где печатают эти случайные числа. Один лист отдают получателю, а второй оставляют у отправителя. При желании пообщаться они используют этот поток случайных чисел в качестве ключевого потока. Нет, история взята не из совсем далекого прошлого. У меня есть настоящий радиоперехват от 15 октября 2014 года: 7 2 6, 7 2 6, 7 2 6. Это позывной. 4 8 3, 4 8 3, 4 8 3. Это номер шифроблокнота. 5 0, 5 0, 5 0. Это количество слов. 8 4 4 7 9 8 4 4 7 9 2 0 5 1 4 2 0 5 1 4 и т. д. 50 таких числовых групп. Не знаю где, где-то не в России сидел какой-нибудь человек с ручкой и карандашом у обычного радиоприемника и записывал эти цифры. Записав их, он достал похожую штуку, сложил их по модулю 10 и получил свое сообщение. Другими словами, это реально работает, и подобное сообщение нельзя взломать. Если действительно были сгенерированы хорошие случайные числа и он впоследстии сжег бумажку с ключом, то осуществить взлом нельзя никак, совсем.
Но тут есть довольно много проблем. Первая — как нагенерировать по-настоящему хорошие случайные числа. Мир вокруг нас детерминирован, и если мы говорим про компьютеры, они детерминированы полностью.
Во-вторых, доставлять ключи такого размера… если мы говорим про передачу сообщений из 55 цифровых групп, то проделать подобное не очень сложно, а вот передать несколько гигабайт текста — уже серьезная проблема. Следовательно, нужны какие-нибудь алгоритмы, которые, по сути, генерируют псевдослучайные числа на основе какого-нибудь небольшого начального значения и которые могли бы использоваться в качестве таких потоковых алгоритмов. 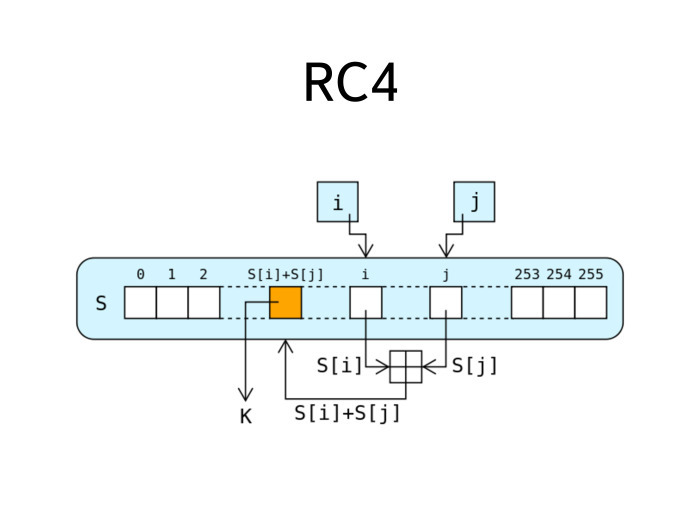
Самый исторически распространенный алгоритм подобного рода называется RC4. Он был разработан Роном Ривестом лет 25 назад и активно использовался очень долго, был самым распространенным алгоритмом для TLS, всех его различных вариантов, включая HTTPS. Но в последнее время RC4 начал показывать свой возраст. Для него существует некоторое количество атак. Он активно используется в WEP. Была одна хорошая лекция Антона, история, которая показывает: плохое применение пристойного даже по нынешним меркам алгоритма шифрования приводит к тому, что компрометируется вся система.
RC4 устроен несложно. На слайде целиком описана его работа. Есть внутренний байтовый стейт из 256 байт. На каждом шаге этого стейта есть два числа, два указателя на разные байты в стейте. И на каждом шаге происходит сложение между этими числами — они помещаются в некоторое место стейта. Полученный оттуда байт является следующим байтом в числовой последовательности. Вращая эту ручку таким образом, выполняя подобное действие на каждом шаге, мы получаем каждый следующий байт. Мы можем получать следующий байт числовой последовательности вечно, потоком.
Большое достоинство RC4 — в том, что он целиком внутрибайтовый, а значит, его программная реализация работает довольно быстро — сильно быстрее, в разы, если не в десятки раз быстрее, чем сравнимый и существовавший примерно в одно время с ним шифр DES. Поэтому RC4 и получил такое распространение. Он долго был коммерческим секретом компании RSA, но потом, где-то в районе 90-х годов, некие люди анонимно опубликовали исходники его устройства в списке рассылки cypherpunks. В результате возникло много драмы, были крики, мол, как же так, какие-то неприличные люди украли интеллектуальную собственность компании RSA и опубликовали ее. RSA начала грозить всем патентами, всевозможными юридическими преследованиями. Чтобы их избежать, все реализации алгоритма, которые находятся в опенсорсе, называются не RC4, а ARC4 или ARCFOUR. А — alleged. Речь идет о шифре, который на всех тестовых кейсах совпадает с RC4, но технически вроде как им не является.
Если вы конфигурируете какой-нибудь SSH или OpenSSL, вы в нем не найдете упоминания RC4, а найдете ARC4 или что-то подобное. Несложная конструкция, он уже старенький, на него сейчас есть атаки, и он не очень рекомендуется к использованию. 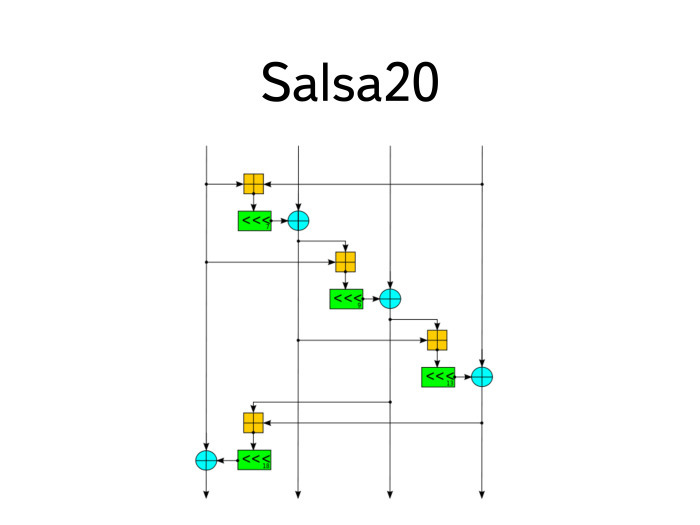
Было несколько попыток его заменить. Наверное, на мой предвзятый взгляд самым успешным стал шифр Salsa20 и несколько его последователей от широко известного в узких кругах персонажа Дэна Берштайна. Линуксоидам он обычно известен как автор qmail.
Salsa20 устроен сложнее, чем DES. Его блок-схема сложная, но он обладает несколькими интересными и классными свойствами. Для начала, он всегда выполняется за конечное время, каждый его раунд, что немаловажно для защиты от тайминг-атак. Это такие атаки, где атакующий наблюдает поведение системы шифрования, скармливая ей разные шифротексты или разные ключи за этим черным ящиком. И, понимая изменения во времени ответа или в энергопотреблении системы, он может делать выводы о том, какие именно процессы произошли внутри. Если вы думаете, что атака сильно надуманная, это не так. Очень широко распространены атаки подобного рода на смарт-карты — очень удобные, поскольку у атакующего есть полный доступ к коробке. Единственное, что он, как правило, не может в ней сделать, — прочитать сам ключ. Это сложно, а делать все остальное он может — подавать туда разные сообщения и пытаться их расшифровать.
Salsa20 устроен так, чтобы он всегда выполнялся за константное одинаковое время. Внутри он состоит всего из трех примитивов: это сдвиг на константное время, а также сложение по модулю 2 и по модулю 32, 32-битных слов. Скорость Salsa20 еще выше, чем у RC4. Он пока что не получил такого широкого распространения в общепринятой криптографии — у нас нет cipher suite для TLS, использующих Salsa20, — но все равно потихоньку становится мейнстримом. Указанный шифр стал одним из победителей конкурса eSTREAM по выбору лучшего поточного шифра. Их там было четыре, и Salsa — один из них. Он потихоньку начинает появляться во всяких опенсорс-продуктах. Возможно, скоро — может, через пару лет — появятся даже cipher suite в TLS с Salsa20. Мне он очень нравится.
Какая проблема с поточными шифрами? Если у вас есть поток данных, передаваемый по сети, поточный шифр для него удобен. К вам влетел пакет, вы его зашифровали и передали. Влетел следующий — приложили эту гамму и передали. Первый байт, второй, третий по сети идут. Удобно.
Если данные, например гигабайтный файл целиком, зашифрованы на диске поточным шифром, то чтобы прочитать последние 10 байт, вам нужно будет сначала сгенерировать гаммы потока шифра на 1 гигабайт, и уже из него взять последние 10 байт. Очень неудобно.
В Salsa указанная проблема решена, поскольку в нем на вход поступает в том числе и номер блока, который надо сгенерировать. Дальше к номеру блока 20 раз применяется алгоритм. 20 раундов — и мы получаем 512 бит выходного потока.
Самая успешная атака — в 8 раундов. Сам он 256-битный, а сложность атаки в 8 раундов — 250 или 251 бит. Считается, что он очень устойчивый, хороший. Публичный криптоанализ на него есть. Несмотря на всю одиозность личности Берштайна в этом аспекте, мне кажется, что штука хорошая и у нее большее будущее.
Исторически поточных шифров было много. Они первые не только в коммерческом шифровании, но и в военном. Там использовалось то, что называлось линейными регистрами сдвига.
Какие тут проблемы? Первая: в классических поточных шифрах, не в Salsa, чтобы расшифровать последнее значение гигабайтного файла, последний байт, вам нужно сначала сгенерировать последовательность на гигабайт. От нее вы задействуете только последний байт. Очень неудобно.
Поточные шифры плохо пригодны для систем с непоследовательным доступом, самый распространенный пример которых — жесткий диск.
Есть и еще одна проблема, о ней мы поговорим дальше. Она очень ярко проявляется в поточных шифрах. Две проблемы в совокупности привели к тому, что здорово было бы использовать какой-нибудь другой механизм.
Другой механизм для симметричного шифрования называется блочным шифром. Он устроен чуть по-другому. Он не генерирует этот ключевой поток, который надо ксорить с нашим шифротекстом, а работает похоже — как таблица подстановок. Берет блок текста фиксированной длины, на выходе дает такой же длины блок текста, и всё.
Размер блока в современных шифрах — как правило, 128 бит. Бывают разные вариации, но как правило, речь идет про 128 или 256 бит, не больше и не меньше. Размер ключа — точно такой же, как для поточных алгоритмов: 128 или 256 бит в современных реализациях, от и до.
Из всех широко распространенных блочных шифров сейчас можно назвать два — DES и AES. DES очень старый шифр, ровесник RC4. У DES сейчас размер блока — 64 бита, а размер ключа — 56 бит. Создан он был в компании IBM под именем Люцифер. Когда в IBM его дизайном занимался Хорст Фейстель, они предложили выбрать 128 бит в качестве размера блока. А размер ключа был изменяемый, от 124 до 192 бит.
Когда DES начал проходит стандартизацию, его подали на проверку в том числе и в АНБ. Оттуда он вернулся с уменьшенным до 64 бит размером блока и уменьшенным до 56 бит размером ключа. 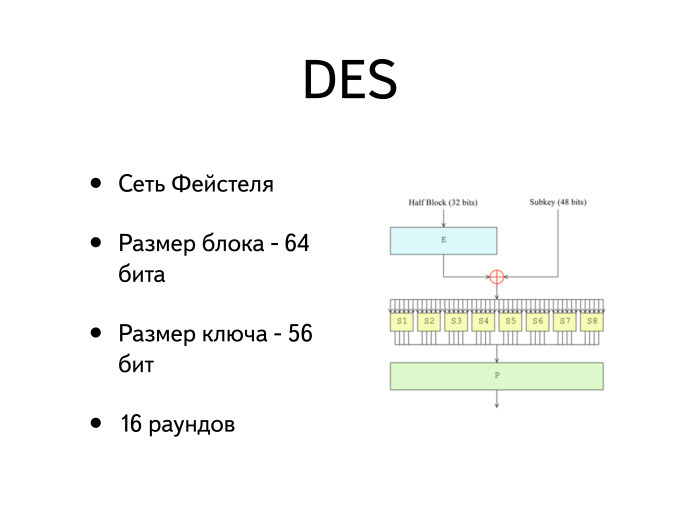
20 лет назад вся эта история наделала много шума. Все говорили — наверняка они туда встроили закладку, ужасно, подобрали такой размер блока, чтобы получить возможность атаковать. Однако большое достоинство DES в том, что это первый шифр, который был стандартизован и стал тогда основой коммерческой криптографии.
Его очень много атаковали и очень много исследовали. Есть большое количество всевозможных атак. Но ни одной практически реализуемой атаки до сих пор нет, несмотря на его довольно почтенный возраст. Единственное, размер ключа в 56 бит сейчас просто неприемлемый и можно атаковать полным перебором.
Как устроен DES? Фейстель сделал классную штуку, которую называют сетью Фейстеля. Она оперирует блоками. Каждый блок, попадающий на вход, делится на две части: левую и правую. Левая часть становится правой без изменений. Правая часть ксорится с результатом вычисления некой функции, на вход которой подается левая часть и ключ. После данного преобразования правая часть становится левой. 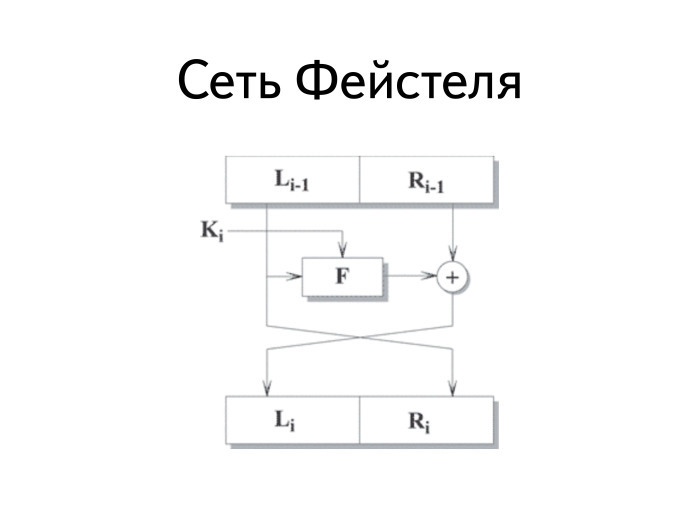
У нее есть несколько интересных достоинств. Первое важное достоинство: функция F может быть любой. Она не должна обладать свойствами обратимости, она может и не быть линейной или нелинейной. Все равно шифр остается симметричным.
Второе очень удобное свойство: расшифровка устроена так же, как шифрование. Если нужно расшифровать данную сеть, вы в прежний механизм вместо открытого текста засовываете шифротекст и на выходе вновь получаете открытый текст.
Почему это удобно? 30 лет назад удобство являлось следствием того, что шифраторы были аппаратными и заниматься дизайном отдельного набора микросхем для шифрования и для расшифровки было трудоемко. А в такой конструкции все очень здорово, фактически мы можем один блок использовать для разных задач.
В реальной ситуации такая конструкция — один раунд блочного шифра, то есть в реальном шифре она выполняется 16 раз с разными ключами. На каждом 16 раунде генерируется отдельный ключ и 16 раундовых подключей, каждый из которых применяется на каждом раунде для функции F.
Раунд тоже выглядит довольно несложно — он состоит всего из двух-трех операций. Первая операция: размер попавшегося полублока становится равен 32 бита, полубок проходит функцию расширения, на вход попадает 32 бита. Дальше мы по специальной несекретной таблице немного добавляем к 32 битам, превращая их в 48: некоторые биты дублируются и переставляются, такая гребеночка.
Потом мы его ксорим с раундовым ключом, размер которого — тоже 48 бит, и получаем 48-битное значение.
Затем оно попадает в набор функций, которые называются S-боксы и преобразуют каждый бит входа в четыре бита выхода. Следовательно, на выходе мы из 48 бит снова получаем 32 бита.
И наконец, окончательная перестановка P. Она опять перемешивает 32 бита между собой. Все очень несложно, раундовая функция максимально простая.
Самое интересное ее свойство заключается в указанных S-боксах: задумано очень сложное превращение 6 бит в 4. Если посмотреть на всю конструкцию, видно, что она состоит из XOR и пары перестановок. Если бы S-боксы были простыми, весь DES фактически представлял бы собой некоторый набор линейных преобразований. Его можно было бы представить как матрицу, на которую мы умножаем наш открытый текст, получая шифротекст. И тогда атака на DES была бы тривиальной: требовалось бы просто подобрать матрицу.
Вся нелинейность сосредоточена в S-боксах, подобранных специальным образом. Существуют разные анекдоты о том, как именно они подбирались. В частности, примерно через 10 лет после того, как DES был опубликован и стандартизован, криптографы нашли новый тип атак — дифференциальный криптоанализ. Суть атаки очень простая: мы делаем мелкие изменения в открытом тексте — меняя, к примеру, значение одного бита с 0 на 1 — и смотрим, что происходит с шифротекстом. Выяснилось, что в идеальном шифре изменение одного бита с 0 на 1 должно приводить к изменению ровно половины бит шифротекста. Выяснилось, что DES, хоть он и был сделан перед тем, как открыли дифференциальный криптоанализ, оказался устойчивым к этому типу атак. В итоге в свое время возникла очередная волна паранойи: мол, АНБ еще за 10 лет до открытых криптографов знало про существование дифференциального криптоанализа, и вы представляете себе, что оно может знать сейчас.
Анализу устройства S-боксов посвящена не одна сотня статей. Есть классные статьи, которые называются примерно так: особенности статистического распределения выходных бит в четвертом S-боксе. Потому что шифру много лет, он досконально исследован в разных местах и остается достаточно устойчивым даже по нынешним меркам.
56 бит сейчас уже можно просто перебрать на кластере машин общего назначения — может, даже на одном. И это плохо. Что можно предпринять?
Просто сдвинуть размер ключа нельзя: вся конструкция завязана на его длину. Triple DES. Очевидный ответ был таким: давайте мы будем шифровать наш блок несколько раз, устроим несколько последовательных шифрований. И здесь всё не слишком тривиально.
Допустим, мы берем и шифруем два раза. Для начала нужно доказать, что для шифрований k1 и k2 на двух разных ключах не существует такого шифрования на ключе k3, что выполнение двух указанных функций окажется одинаковым. Здесь вступает в силу свойство, что DES не является группой. Тому существует доказательство, пусть и не очень тривиальное.
Окей, 56 бит. Давайте возьмем два — k1 и k2. 56 + 56 = 112 бит. 112 бит даже по нынешним меркам — вполне приемлемая длина ключа. Можно считать нормальным всё, что превышает 100 бит. Так почему нельзя использовать два шифрования, 112 бит?
Одно шифрование DES состоит из 16 раундов. Сеть применяется 16 раз. Изменения слева направо происходят 16 раз. И он — не группа. Есть доказательство того, что не существует такого ключа k3, которым мы могли бы расшифровать текст, последовательно зашифрованный выбранными нами ключами k1 и k2.
Есть атака. Давайте зашифруем все возможные тексты на каком-нибудь ключе, возьмем шифротекст и попытаемся его расшифровать на всех произвольных ключах. И здесь, и здесь получим 2 56 вариантов. И где-то они сойдутся. То есть за два раза по 2 56 вариантов — плюс память для хранения всех расшифровок — мы найдем такую комбинацию k1 и k2, при которых атака окажется осуществимой.
Эффективная стойкость алгоритма — не 112 бит, а 57, если у нас достаточно памяти. Нужно довольно много памяти, но тем не менее. Поэтому решили — так работать нельзя, давайте будем шифровать три раза: k1, k2, k3. Конструкция называется Triple DES. Технически она может быть устроена по-разному. Поскольку в DES шифрование и дешифрование — одно и то же, реальные алгоритмы иногда выглядят так: зашифровать, расшифровать и снова расшифровать — чтобы выполнять операции в аппаратных реализациях было проще.
Наша обратная реализация Triple DES превратится в аппаратную реализацию DES. Это может быть очень удобно в разных ситуациях для задачи обратной совместимости.
Где применялся DES? Вообще везде. Его до сих пор иногда можно пронаблюдать для TLS, существуют cipher suite для TLS, использующие Triple DES и DES. Но там он активно отмирает, поскольку речь идет про софт. Софт легко апдейтится.
А вот в банкоматах он отмирал очень долго, и я не уверен, что окончательно умер. Не знаю, нужна ли отдельная лекция о том, как указанная конструкция устроена в банкоматах. Если коротко, клавиатура, где вы вводите PIN, — самодостаточная вещь в себе. В нее загружены ключи, и наружу она выдает не PIN, а конструкцию PIN-блок. Конструкция зашифрована — например, через DES. Поскольку банкоматов огромное количество, то среди них много старых и до сих пор можно встретить банкомат, где внутри коробки реализован даже не Triple DES, а обычный DES.
Однажды DES стал показывать свой возраст, с ним стало тяжело, и люди решили придумать нечто поновее. Американская контора по стандартизации, которая называется NIST, сказала: давайте проведем конкурс и выберем новый классный шифр. Им стал AES.
DES расшифровывается как digital encrypted standard. AES — advanced encrypted standard. Размер блока в AES — 128 бит, а не 64. Это важно с точки зрения криптографии. Размер ключа у AES — 128, 192 или 256 бит. В AES не используется сеть Фейстеля, но он тоже многораундовый, в нем тоже несколько раз повторяются относительно примитивные операции. Для 128 бит используется 10 раундов, для 256 — 14.
Сейчас покажу, как устроен каждый раунд. Первый и последний раунды чуть отличаются от стандартной схемы — тому есть причины.
Как и в DES, в каждом раунде AES есть свои раундовые ключи. Все они генерируются из ключа шифрования для алгоритма. В этом месте AES работает так же, как DES. Берется 128-битный ключ, из него генерируется 10 подключей для 10 раундов. Каждый подключ, как и в DES, применяется на каждом конкретном раунде.
Каждый раунд состоит из четырех довольно простых операций. Первый раунд — подстановка по специальной таблице.
В AES мы строим байтовую матрицу размером 4 на 4. Каждый элемент матрицы — байт. Всего получается 16 байт или 128 бит. Они и составляют блок AES целиком.
Вторая операция — побайтовый сдвиг.
Устроен он несложно, примитивно. Мы берем матрицу 4 на 4. Первый ряд остается без изменений, второй ряд сдвигается на 1 байт влево, третий — на 2 байта, четвертый — на 3, циклично.
Далее мы производим перемешивание внутри колонок. Это тоже очень несложная операция. Она фактически переставляет биты внутри каждой колонки, больше ничего не происходит. Можно считать ее умножением на специальную функцию.
Четвертая, вновь очень простая операция — XOR каждого байта в каждой колонке с соответствующим байтом ключа. Получается результат.
В первом раунде лишь складываются ключи, а три других операции не используются. В последнем раунде не происходит подобного перемешивания столбцов:
Дело в том, что это не добавило бы никакой криптографической стойкости и мы всегда можем обратить последний раунд. Решили не тормозить конструкцию лишней операцией.
Мы повторяем 4 описанных шага 10 раз, и на выходе из 128-битного блока снова получаем 128-битный блок.
Какие достоинства у AES? Он оперирует байтами, а не битами, как DES. AES намного быстрее в софтовых реализациях. Если сравнить скорость выполнения AES и DES на современной машине, AES окажется в разы быстрее, даже если говорить о реализации исключительно в программном коде.
Производители современных процессоров, Intel и AMD, уже разработали ассемблерные инструкции для реализации AES внутри чипа, потому что стандарт довольно несложный. Как итог — AES еще быстрее. Если через DES на современной машинке мы можем зашифровать, например, 1-2 гигабита, то 10-гигабитный AES-шифратор находится рядом и коммерчески доступен обычным компаниям.
Блочный алгоритм шифрует блок в блок. Он берет блок на 128 или 64 бита и превращает его в блок на 128 или 64 бита.
А что мы будем делать, если потребуется больше, чем 16 байт?
Первое, что приходит в голову, — попытаться разбить исходное сообщение на блоки, а блок, который останется неполным, дополнить стандартной, известной и фиксированной последовательностью данных.
Да, очевидно, побьем всё на блоки по 16 байт и зашифруем. Такое шифрование называется ECB — electronic code boot, когда каждый из блоков по 16 байт в случае AES или по 8 байт в случае DES шифруется независимо. 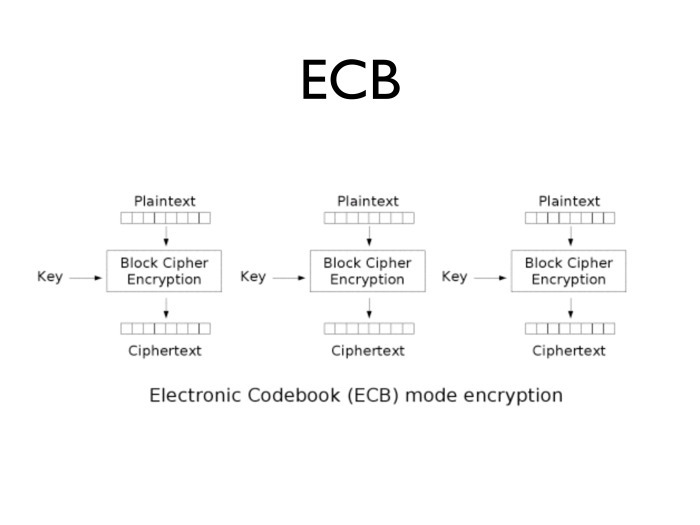
Шифруем каждый блок, получаем шифротекст, складываем шифротексты и получаем полный результат. 
Примерно так выглядит картинка, зашифрованная в режиме ECB. Даже если мы представим себе, что шифр полностью надежен, кажется, что результат менее чем удовлетворительный. В чем проблема? В том, что это биективное отображение. Для одинакового входа всегда получится одинаковый выход, и наоборот — для одинакового шифротекста всегда получится одинаковый открытый текст.
Надо бы как-нибудь исхитриться и сделать так, чтобы результат на выходе все время получался разным, в зависимости от местонахождения блока — несмотря на то, что на вход подаются одинаковые блоки шифротекста. Первым способом решения стал режим CBC. 
Мы не только берем ключ и открытый текст, но и генерируем случайное число, которое не является секретным. Оно размером с блок. Называется оно инициализационным вектором.
При шифровании первого блока мы берем инициализационный вектор, складываем его по модулю 2 с открытым текстом и шифруем. На выходе — шифротекст. Дальше складываем полученный шифротекст по модулю 2 со вторым блоком и шифруем. На выходе — второй блок шифротекста. Складываем его по модулю 2 с третьим блоком открытого текста и шифруем. На выходе получаем третий блок шифротекста. Здесь видно сцепление: мы каждый следующий блок сцепляем с предыдущим.
В результате получится картинка, где всё, начиная со второго блока, равномерно размазано, а первый блок каждый раз зависит от инициализационного вектора. И она будет абсолютно перемешана. Здесь все неплохо.
Однако у CBC есть несколько проблем.
О размере блока. Представьте: мы начали шифровать и, допустим, у нас DES. Если бы DES был идеальным алгоритмом шифрования, выход DES выглядел бы как равномерно распределенные случайные числа длиной 64 бита. Какова вероятность, что в выборке из равномерно распределенных случайных чисел длиной 64 бита два числа совпадут для одной операции? 1/(2 64 ). А если мы сравниваем три числа? Давайте пока прервемся.