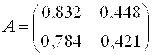для вычисления числа обусловленности необходимо иметь явный вид какой матрицы
2. Вычисление нормы и чисел обусловленности матрицы
Вычисление нормы и чисел обусловленности матрицы
Для понимания всего нижеизложенного материала необходимо учесть, что нормы матриц в MATLAB отличаются от норм векторов.
Пусть А —матрица. Тогда n=norm(A) эквивалентно п=погп(А,2) и возвращает вторую норму, т. е. самое большое сингулярное число А. Функция n=norm(A, 1) возвращает первую норму, т. е. самую большую из сумм абсолютных значений элементов матрицы по столбцам. Норма неопределенности n=norm(A, inf) возвращает самую большую из сумм абсолютных значений элементов матрицы по рядам. Норма Фробениуса (Frobenius) norm(A, ‘fro’) = sqrt(sum(diag(A’A))).
Числа обусловленности матрицы определяют чувствительность решения системы линейных уравнений к погрешностям исходных данных. Следующие функции позволяют найти числа обусловленности матриц.
cond(X) — возвращает число обусловленности, основанное на второй норме, то есть отношение самого большого сингулярного числа X к самому малому. Значение cond(X), близкое к 1, указывает на хорошо обусловленную матрицу;
с = cond(X.p) — возвращает число обусловленности матрицы, основанное на р-норме: norm(X.p)*norm(inv(X),p), где р определяет способ расчета:
р=1 — число обусловленности матрицы, основанное на первой норме;
р=2 — число обусловленности матрицы, основанное на второй норме;
p= ‘fro’ — число обусловленности матрицы, основанное на норме Фробе-ниуса (Frobenius);
р=’inf’ — число обусловленности матрицы, основанное на норме неопределенности.
с = cond(X) — возвращает число обусловленности матрицы, основанное на второй норме.
condeig(A) — возвращает вектор чисел обусловленности для собственных значений А. Эти числа обусловленности — обратные величины косинусов углов между левыми и правыми собственными векторами;
[V.D.s] = condeig(A) — эквивалентно [V,D] = eig(A): s = condeig(A);.
Большие числа обусловленности означают, что матрица А близка к матрице с кратными собственными значениями.
rcond(A) — возвращает обратную величину обусловленности матрицы А по первой норме, используя оценивающий обусловленность метод LAPACK. Если А — хорошо обусловленная матрица, то rcond(A) около 1.00, если плохо обусловленная, то около 0.00. По сравнению с cond функция rcond реализует более эффективный в плане затрат машинного времени, но менее достоверный метод оценки обусловленности матрицы.
Обусловленность слау. Число обусловленности матрицы Понятия согласованных норм матриц и векторов позволяют оценить погрешности, возникающие при численном решени




| скачать Обусловленность СЛАУ. Число обусловленности матрицы Понятия согласованных норм матриц и векторов позволяют оценить погрешности, возникающие при численном решении СЛАУ. Пусть и матрица, и правая часть системы заданы с некоторой погрешностью, тогда наряду с системой Теорема. Пусть правая часть и невырожденная матрица СЛАУ (2.4) вида Au = f, Доказательство. Из (2.5) следует, что Вводя обозначение
Тогда для оценки относительной погрешности решения окончательно получим
При
если в (2.5) положить
В результате получено важное соотношение, показывающее, на сколько возрастают относительные ошибки решения СЛАУ в случае наличия относительных ошибок при задании правых частей и элементов матриц.
называется числом обусловленности матрицы A. Число обусловленности определяет, насколько погрешность входных данных может повлиять на решение системы (2.1). Почти очевидно, что всегда
При Пример. Решением системы будет пара чисел Внесем возмущение в правые части системы: При этом решение заметно изменится: u = 2,97; v = –0,99. Воспользовавшись выбранными согласованными нормами, получим Значит Рассмотрим еще одно важное свойство. Число обусловленности матрицы, как было показано ранее, можно определить, как Параметр ν(f), характеризующий обусловленность системы, зависит от правых частей. Более тонкая его оценка есть Можно также показать, что для симметричной матрицы А имеет место Среды прямых методов численного решения СЛАУ широко используется также LU-разложение матрицы ^ А и метод Холецкого (или метод квадратного корня). Если матрица А представима в виде произведений матриц LU, то СЛАУ может быть представлена в виде Перепишем (2.13), вводя вспомогательный вектор v, в следующем виде Решение СЛАУ свелось к последовательному решению двух систем с треугольными матрицами. Первый этап решения системы Lv = f: откуда можно вычислить все vk последовательно по формулам
Далее, рассмотрим систему Uu = v или
решение которой находятся в обратном порядке, т.е. при k = n – 1,…,1 по очевидным формулам Условия существования такого разложения даются следующей теоремой [5] (без доказательства). Теорема. Если все главные миноры квадратной матрицы ^ А отличны от нуля, то существуют единственные нижняя и верхняя треугольные матрицы L = <lij> и U = <dij> такие, что А = LU. При этом все диагональные коэффициенты матрицы L фиксированы и равны единице. Опишем алгоритм нахождения элементов lij dij матриц L, U. Выписав равенство А = LU в компонентах, получим Выполнив умножение матриц, приходим к системе линейных уравнений размером n n: Специфика этой системы позволяет решить ее последовательно. Из первой строки находим d1j = a1j (j = 1,…, n). Из уравнений, входящих в первый столбец приведенной выше системы, находим li1 = ai1/d11, i = 1,…, n. Теперь можно из уравнений второй строки найти d2j = a2j – l21d1j, j = 2,…, n, а из уравнений, входящих во второй столбец, получим li2 = d Можно выписать общий вид этих формул Итерационные методы решения СЛАУ Метод простой итерации Рассмотрим систему линейных алгебраических уравнений Проведем несколько равносильных преобразований. Умножим обе части системы на один и тот же скалярный множитель τ, затем прибавим к правой и левой частям системы вектор u. Систему уравнений можно теперь записать в виде, удобном для итераций Теперь построим последовательность приближений к решению системы. Выберем произвольный вектор u0 — начальное приближение к решению. Чаще всего его просто полагают нулевым вектором. Скорее всего, начальное приближение не удовлетворяет (2.15) и, следовательно, исходной системе. При подстановке его в исходное уравнение возникает невязка r0 = f – Au0. Вычислив невязку, с помощью (2.15) можно уточнить приближение к решению, считая что По первому приближению снова вычисляется невязка, процесс продолжается. В ходе итерации получаем Существуют другие формы записи метода итераций, например Канонической формой записи двухслойного итерационного процесса называется следующая: При Теорема (достаточное условие сходимости метода простой итерации). Итерационный процесс (2.16) сходится к решению U СЛАУ Доказательство. Пусть U — точное решение системы (2). Вычитая из (2.16)-(2.15), получим 6.1. Решение систем линейных алгебраических уравнений. Обусловленность матрицыПри исследовании численных методов для решения математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма. Для каждой математической задачи принято рассматривать вопрос о ее корректности. Определение. Говорят, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от входных данных. Будем считать, что решение и правая часть задачи (6.1) принадлежат линейному пространству H, состоящему из N-мерных векторов. Введем в H норму, для которой выполнено: ||X||>0, для всех Х≠0 ||α X||=| α| ||X||, для любого числа А и Х ||X+Y||≤||X||+||Y||, для любых X и Y Определение. Нормой матрицы А, подчиненной данной норме векторов, называется число Эта оценка выражает факт непрерывной зависимости решения от правой части, то есть показывает, что || δx|| Стремится к нулю при || δf ||Стремящемся к нулю. Наличие устойчивости очень важно при численном решении систем уравнений, так как никогда нельзя задать правую часть F точно. Погрешность δf возникает в результате округления. Определение. Число ρ(A)= ρ(A)= Где λMax , λmin – максимальное и минимальное по модулю собственные значения матрицы A. Матрицы с большим числом обусловленности называются плохо обусловленными. При численном решении систем с такими матрицами возможно сильное накопление погрешности. При небольших изменениях правой части погрешность решения может оказаться значительной. Например, для матрицы Число обусловленности ρ(A)= Если взять матрицу
|

 (2.5)
(2.5)
 , получили приращения
, получили приращения  и
и  соответственно. Пусть существует обратная матрица А –1 и выполнены условия
соответственно. Пусть существует обратная матрица А –1 и выполнены условия 
 где
где  В этом случае оценка относительной погрешности решения
В этом случае оценка относительной погрешности решения  удовлетворяет неравенству
удовлетворяет неравенству
 Переходя в этом равенстве к норме и использовав неравенство треугольника, получаем
Переходя в этом равенстве к норме и использовав неравенство треугольника, получаем  или
или
 перепишем последнее равенство в виде
перепишем последнее равенство в виде Заметим, что
Заметим, что  т.к.
т.к.  .
. . (2.6)
. (2.6) получаем оценку при наличии погрешности только правых частей
получаем оценку при наличии погрешности только правых частей , (2.7)
, (2.7) то
то . (2.8)
. (2.8) , (2.9)
, (2.9) Действительно
Действительно .
. , то ошибки входных данных слабо сказываются на решении и система (2.1) считается хорошо обусловленной. При
, то ошибки входных данных слабо сказываются на решении и система (2.1) считается хорошо обусловленной. При  система является плохо обусловленной.
система является плохо обусловленной.
 .
.

 ,
,  (это очень малая величина),
(это очень малая величина),  ,
,  .
.
 , что согласуется с результатами решения возмущенной и невозмущенной задач. Для невозмущенной задачи
, что согласуется с результатами решения возмущенной и невозмущенной задач. Для невозмущенной задачи 

 если
если  при
при  Можно ли найти более тонкую оценку отношения
Можно ли найти более тонкую оценку отношения  учитывающую зависимость обусловленности СЛАУ от выбора правых частей. В этом случае параметр обусловленности системы, вообще говоря, зависит и от f, и от Δf и удовлетворяет неравенству
учитывающую зависимость обусловленности СЛАУ от выбора правых частей. В этом случае параметр обусловленности системы, вообще говоря, зависит и от f, и от Δf и удовлетворяет неравенству  Его можно определить как точную верхнюю грань отношения
Его можно определить как точную верхнюю грань отношения  по Δf, что соответствует наихудшей ситуации. Тогда
по Δf, что соответствует наихудшей ситуации. Тогда


 причем
причем  Так как такую оценку провести не всегда возможно, то чаще используется точная верхняя грань
Так как такую оценку провести не всегда возможно, то чаще используется точная верхняя грань  Такая оценка, конечно, может быть существенно завышенной.
Такая оценка, конечно, может быть существенно завышенной. т.е. обусловленность СЛАУ зависит от ее спектральных свойств. Это следует из определения третьей нормы матрицы
т.е. обусловленность СЛАУ зависит от ее спектральных свойств. Это следует из определения третьей нормы матрицы  и соотношения
и соотношения  которое предлагается доказать самостоятельно.
которое предлагается доказать самостоятельно. (2.13)
(2.13)
 (2.14)
(2.14)
 ;
;  .
. .
.

 (ai2 – li1d12), i = 2,…, n и так далее. Последним вычисляется элемент
(ai2 – li1d12), i = 2,…, n и так далее. Последним вычисляется элемент 
 i j,
i j, i > j.
i > j.
 Эквивалентная формулировка метода, называемого методом простых итераций, заключается в следующем. Решение (2.15) находится как предел последовательности
Эквивалентная формулировка метода, называемого методом простых итераций, заключается в следующем. Решение (2.15) находится как предел последовательности  приближений, члены которой связаны рекуррентным соотношением (оно эквивалентно приведенному выше, из записи исключен вектор невязки):
приближений, члены которой связаны рекуррентным соотношением (оно эквивалентно приведенному выше, из записи исключен вектор невязки): (2.16)
(2.16) (или любому произвольному вектору). Если предел такой последовательности существует, то говорят о сходимости итерационного процесса к решению СЛАУ.
(или любому произвольному вектору). Если предел такой последовательности существует, то говорят о сходимости итерационного процесса к решению СЛАУ. (2.17)
(2.17) (2.18)
(2.18) ,
,  последняя формула соответствует однопараметрическому итерационному процессу — рассмотренному выше методу простых итераций. При
последняя формула соответствует однопараметрическому итерационному процессу — рассмотренному выше методу простых итераций. При  — n—шаговому явному итерационному процессу, при
— n—шаговому явному итерационному процессу, при  ,
,  — методу простой итерации без итерационного параметра. В случае, когда
— методу простой итерации без итерационного параметра. В случае, когда  итерационный метод называется неявным — для вычисления следующего приближения к решению придется решать (как правило, более простую, чем исходную) систему линейных уравнений.
итерационный метод называется неявным — для вычисления следующего приближения к решению придется решать (как правило, более простую, чем исходную) систему линейных уравнений. со скоростью геометрической прогрессии при выполнении условия:
со скоростью геометрической прогрессии при выполнении условия:  .
. , или, обозначив погрешность
, или, обозначив погрешность  , получим для эволюции погрешности уравнение
, получим для эволюции погрешности уравнение  Справедлива цепочка неравенств:
Справедлива цепочка неравенств: где
где 
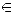 H ,
H , , для всех Х≠0
, для всех Х≠0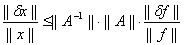 .
. называется числом обусловленности матрицы A и характеризует степень зависимости относительной погрешности решения от относительной погрешности правой части. В случае самосопряженной матрицы A =A* это число равно
называется числом обусловленности матрицы A и характеризует степень зависимости относительной погрешности решения от относительной погрешности правой части. В случае самосопряженной матрицы A =A* это число равно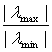 ,
,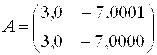
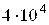 , И если взять за правую часть системы вектор F= (1,0000, 1,0000)T, то получим решение X=(0,3333, 0,0000)T. Решение «возмущенной» системы с правой частью Fδ = (0,9998, 1,0000)T равно Xε=(5,0000, 2,0000)T.
, И если взять за правую часть системы вектор F= (1,0000, 1,0000)T, то получим решение X=(0,3333, 0,0000)T. Решение «возмущенной» системы с правой частью Fδ = (0,9998, 1,0000)T равно Xε=(5,0000, 2,0000)T.