до какого напряжения u необходимо зарядить конденсатор емкостью c 20пф
Заряд и разряд конденсатора
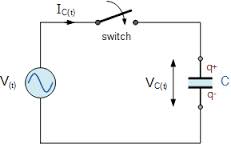
Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. 1 показана схема заряда конденсатора. Конденсатор С присоединен к зажимам генератора. При помощи ключа можно замкнуть или разомкнуть цепь. Рассмотрим подробно процесс заряда конденсатора.
Для того чтобы обкладки конденсатора зарядились, необходимо, чтобы одна из них приобрела, а другая потеряла некоторое количество электронов. Перенос электронов от одной обкладки к другой совершается по внешней цепи электродвижущей силой генератора, а сам процесс перемещения зарядов по цепи есть не что иное, как электрический ток, называемый зарядным емкостным током I зар.
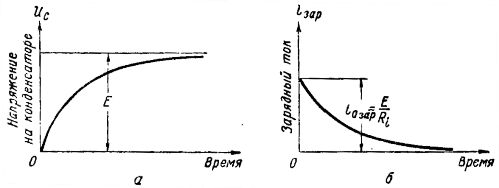
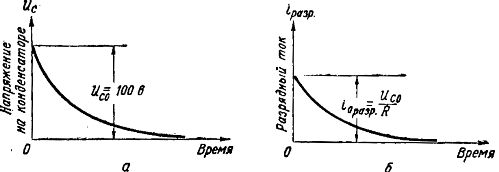
Зарядный ток в цени протекает обычно тысячные доли секунды до тех пор, пока напряжение на конденсаторе достигнет величины, равной э. д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.
Рис. 2. Графики напряжения и тока при заряде конденсатора
Отсюда видно, что с увеличением Uс уменьшается i зар и при Uс = E зарядный ток становится равным нулю.
Про закон Ома подробнее смотрите здесь: закон Ома для участка цепи
Продолжительность процесса заряда конденсатора зависит от двух величии:
2) от емкости конденсатора С.
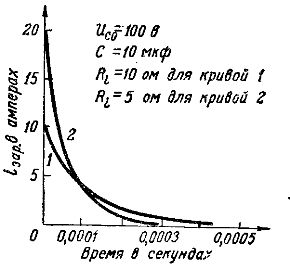
На рис. 2 показаны графики нарядных токов для конденсатора емкостью 10 мкф: кривая 1 соответствует процессу заряда от генератора с э. д. с. Е = 100 В и с внутренним сопротивлением R i = 10 Ом, кривая 2 соответствует процессу заряда от генератора с такой же э. д. с, но с меньшим внутренним сопротивлением: R i = 5 Ом.
Из сравнения этих кривых видно, что при меньшем внутреннем сопротивлении генератора сила нарядного тока в начальный момент больше, и поэтому процесс заряда происходит быстрее.
Рис. 2. Графики зарядных токов при разных сопротивлениях
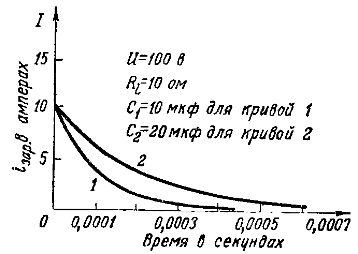
На рис. 3 дается сравнение графиков зарядных токов при заряде от одного и того же генератора с э. д. с. Е = 100 В и внутренним сопротивлением R i = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).
Величина начального зарядного тока io зар = Е/ Ri = 100/10 = 10 А одинакова для обоих конденсаторов, по так как конденсатор большей емкости накапливает большее количество электричества, то зарядный его ток должен проходить дольше, и процесс заряда получается более длительным.
Рис. 3. Графики зарядных токов при разных емкостях
Отключим заряженный конденсатор от генератора и присоединим к его обкладкам сопротивление.
На обкладках конденсатора имеется напряжение U с, поэтому в замкнутой электрической цепи потечет ток, называемый разрядным емкостным током i разр.
На рис. 4, а показан график уменьшения напряжения на конденсаторе при разряде от величины Uc о =100 В до нуля, причем напряжение уменьшается сначала быстро, а затем медленнее.
На рис. 4,б показан график изменения разрядного тока. Сила разрядного тока зависит от величины сопротивления R и по закону Ома i разр = Uc / R
Рис. 4. Графики напряжения и токов при разряде конденсатора
В начальный момент, когда напряжение па обкладках конденсатора наибольшее, сила разрядного тока также наибольшая, а с уменьшением Uc в процессе разряда уменьшается и разрядный ток. При Uc=0 разрядный ток прекращается.
Продолжительность разряда зависит:
1) от емкости конденсатора С
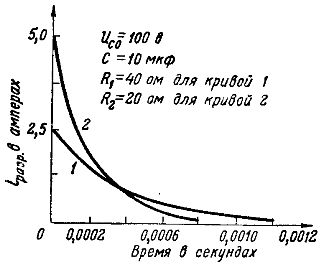
Рис. 5. Графики разрядных токов при разных сопротивлениях
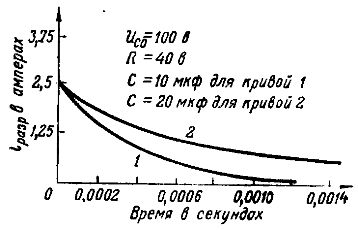
Разряд происходит медленнее также тогда, когда емкость конденсатора велика. Получается это потому, что при большей емкости на обкладках конденсатора имеется большее количество электричества (больший заряд) и для стекания заряда потребуется больший промежуток времени. Это наглядно показывают графики разрядных токов для двух конденсаторов раиной емкости, заряженных до одного и того же напряжения 100 В и разряжающихся на сопротивление R =40 Ом (рис. 6 : кривая 1 — для конденсатора емкостью 10 мкф и кривая 2 — для конденсатора емкостью 20 мкф).
Рис. 6. Графики разрядных токов при разных емкостях
Из рассмотренных процессов можно сделать вывод, что в цепи с конденсатором ток проходит только в моменты заряда и разряда, когда напряжение на обкладках меняется.
Объясняется это тем, что при изменении напряжения изменяется величина заряда на обкладках, а для этого требуется перемещение зарядов по цепи, т. е. по цепи должен проходить электрический ток. Заряженный конденсатор не пропускает постоянный ток, так как диэлектрик между его обкладками размыкает цепь.
В процессе заряда конденсатор накапливает энергию, получая ее от генератора. При разряде конденсатора вся энергия электрического поля переходит в тепловую энергию, т. е. идет на нагрев сопротивления, через которое разряжается конденсатор. Чем больше емкость конденсатора и напряжение на его обкладках, тем больше будет энергия электрического поля конденсатора. Величина энергии, которой обладает конденсатор емкостью С, заряженный до напряжения U, равна: W = W с = С U 2 /2
Пример. Конденсатор С=10 мкф заряжен до напряжении U в = 500 В. Определить энергию, которая выделится в вило тепла на сопротивлении, через которое разряжается конденсатор.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
До какого напряжения u необходимо зарядить конденсатор емкостью c 20пф
Четыре конденсатора одинаковой электроёмкости C = 25 пФ соединены так, как показано на схеме. Определите электроёмкость полученной батареи конденсаторов. Ответ выразите в пикофарадах.
При параллельном соединении конденсаторов их ёмкости складываются. При последовательном соединении общая ёмкость конденсаторов находится по формуле:
Отсюда 
В цепи, схема которой изображена на рисунке, по очереди замыкают ключи 
выжидая каждый раз достаточно длительное время до окончания процессов зарядки конденсаторов. Какое количество теплоты выделится в резисторе после замыкания ключа 
? До его замыкания все остальные ключи уже были замкнуты. Параметры цепи: 
После включения пятого конденсатора произойдет быстрое перераспределение заряда. В результате будет параллельное соединение пяти конденсаторов. Общий заряд 
Общая емкость при параллельном соединении 
напряжение на всех конденсаторах будет одинаковым и равным U.
В результате зарядки всех пяти конденсаторов пройдет заряд 
Источником тока будет совершена работа 
которая пойдет на изменение потенциальной энергии конденсаторов и на выделение теплоты на резисторе: 
Энергия заряженных конденсаторов равна 
Таким образом в резисторе после замыкания пятого ключа выделится теплота
Систему, состоящую из четырёх одинаковых изначально незаряженных последовательно соединённых конденсаторов, подключают к источнику постоянного напряжения. Дождавшись зарядки конденсаторов, обкладки двух из них замыкают при помощи куска проволоки. Как в результате этого изменятся суммарная электроёмкость данной системы конденсаторов и заряд каждого из двух других конденсаторов?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Суммарная электроёмкость системы конденсаторов | Заряд каждого из двух других 1) В первом случае суммарная емкость последовательно соединенных конденсаторов равнялась 2) В первом случае напряжение на каждом конденсаторе равно двух конденсаторов равен напряжение станет равным Аналоги к заданию № 24958: 24991 Все В электрической цепи, схема которой изображена на рисунке, ёмкости конденсаторов равны C1 = 1 мкФ, C2 = 2 мкФ, C3 = 3 мкФ, C4 = 4 мкФ, C5 = 5 мкФ, и все они первоначально не заряжены. Какой заряд установится на конденсаторе C5 после подключения к этой цепи источника с напряжением U = 10 В? 1. Правая часть цепи может быть представлена в виде конденсатора с ёмкостью 2. Суммарная ёмкость всех конденсаторов определяется по формуле для последовательного их соединения
3. Заряды на всех трёх конденсаторах одинаковы и равны
4. Напряжения на конденсаторах обратно пропорциональны их ёмкостям и в сумме равны
5. В правой части цепи параллельно соединены конденсатор C3 с зарядом q 6. Заряд q распределяется между C3 и C45 пропорционально их ёмкостям, откуда где 7. Чтобы не загромождать ответ для q5, проведем численный расчёт: Аналоги к заданию № 24972: 25005 Все Систему, состоящую из трёх одинаковых изначально незаряженных последовательно соединённых конденсаторов, подключают к источнику постоянного напряжения. Дождавшись зарядки конденсаторов, обкладки одного из них замыкают при помощи куска проволоки. Как в результате этого изменятся суммарная электроёмкость данной системы конденсаторов и энергия, запасённая в каждом из двух других конденсаторов? Для каждой величины определите соответствующий характер изменения: Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
При соединении проводником пластин двух конденсаторов в системе останется два последовательно соединенных конденсатора, суммарная емкость которых станет равной 
Значит, суммарная емкость конденсаторов увеличилась (1).
а заряд каждого из
Во втором случае на каждом конденсаторе
а заряд на каждом конденсаторе 
Таким образом, заряд увеличится (1).
(см. рис.), так что вся цепь состоит из трёх последовательно соединённых конденсаторов C1, 
и равна
откуда
а q = q3 + q45.
При соединении проводником пластин одного из конденсаторов в системе останется два последовательно соединенных конденсатора, суммарная емкость которых станет равной 
а энергия двух заряженных конденсаторов равна 
Во втором случае на каждом конденсаторе напряжение станет равным 
Таким образом, энергия увеличится (1).
и 
подключена к источнику постоянного тока с ЭДС 
и внутренним сопротивлением 
(см. рисунок). Определите энергию конденсатора 
и 
и 
соединены в пары параллельно, а образовавшиеся пары — последовательно. Значит, общая электроёмкость системы
так как пары соединены последовательно.
равняется 
равняется 
Следовательно, уменьшение емкости контура приводит к увеличению частоты (Б — 1).
Поскольку энергия колебаний не изменяется, максимальное значение энергии электрического поля в контуре сохраняется. Следовательно, уменьшение емкости контура приводит к увеличению напряжения на втором конденсаторе (В — 1): 
и одинаковыми зарядами q4 = q5 = q45, так что 
У получившихся прямоугольных конденсаторов площадь в два раза меньше исходной, и значит, вдвое меньшая ёмкость — 48 пФ. Ёмкость последовательно соединённых конденсаторов можно найти по формуле: 
и
а второй раз — через резистор 
Во сколько раз во втором случае тепло, выделившееся на резисторе, больше по сравнению с первым? Излучением пренебречь.
Поскольку ёмкость конденсатора не изменяется, запасаемая в нём энергия в обоих случаях совпадает: 
Работа источника также не изменяется, так как заряд конденсатора в обоих случаях одинаков: 
Следовательно, тепло, выделяющееся на резисторе также не изменяется.
«в лоб» использовать нельзя. Если все аккуратно посчитать, то получается, что тепло действительно не зависит от величины сопротивления (оно будет выделяться, даже если формально положить 
(это не противоречие, это просто означает, что в задаче о зарядке конденсатора пренебрегать сопротивлением соединительных проводов нельзя)).
и катушки индуктивностью 
равен 
Таким образом контур 1 имеет период 
контур 2 — период 
(Б — 2).
Следовательно, ёмкости колебательных контуров 3 и 4 равны соответственно 
а значит, период колебаний в контуре 3 равен 
(А — 3), а в контуре 4 — 
Ом и 
Ом, а ёмкости конденсаторов 
мкФ и 
мкФ. В начальном состоянии ключ К разомкнут, а конденсаторы не заряжены. Через некоторое время после замыкания ключа в системе установится равновесие. Какое количество теплоты выделится в цепи к моменту установления равновесия?
— разряжен (его пластины соединены между собой через резисторы): 
При этом через батарею пройдёт заряд 
:
Эта работа переходит в энергию конденсаторов и теплоту:
одинаков, потенциал на обоих концах резистора 
одинаков. Получаем, что конденсатор 
ключ перевели в положение 2. К моменту 
на резисторе R выделилось количество теплоты 
Сила тока в цепи в этот момент равна 
Чему равно сопротивление резистора R? ЭДС батареи 
её внутреннее сопротивление 
ёмкость конденсатора 
Потерями на электромагнитное излучение пренебречь.
Энергия электромагнитного поля в конденсаторе 
где 
— остаточное напряжение на конденсаторе в момент времени 
Работа источника заключается в переносе заряда с одной пластины конденсатора на другую и, следовательно, равна следующей величине: 
значит
. Тогда действительно, как Вы и говорите, зарядка будет происходить по экспоненте, показатель которой зависит от нашего сопротивления и емкости конденсатора. Если теперь воспользоваться законом Джоуля-Ленца и посчитать, какое тепло выделится на резисторе за бесконечное время, требуемое на зарядку, то окажется, что ответ не зависит от величины сопротивления и равен в точности конечной энергии конденсатора. В сумме с энергией конденсатора они в точности дадут работу источника. Подобная задача у автора, видимо, возникла именно из такого рассмотрения: «Раз ответ не зависит от сопротивления, то зачем его указывать!». Также в условии нет указания на то, что нужно считать сопротивление проводов нулевым. Вот этим мне данная задача и нравится. Так что уж лучше исправлять все другие задачи, и добавлять там текст про нулевое сопротивление, чем что-то менять здесь.