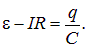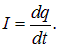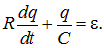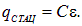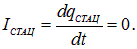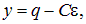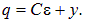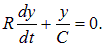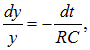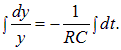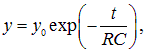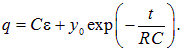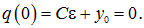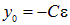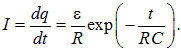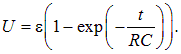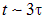до какого напряжения заряжается конденсатор
Емкостное сопротивление
О заряде конденсатора.
Замкнем цепь. В цепи пойдет ток заряда конденсатора. Это значит что с левой обкладки конденсатора часть электронов уйдет в провод, а из провода на правую обкладку зайдет такое же количество электронов. Обе обкладки будут заряжены разноименными зарядами одинаковой величины.
Между обкладками в диэлектрике будет электрическое поле.
А теперь разомкнем цепь. Конденсатор останется заряженным. Закоротим куском провода его обкладки. Конденсатор мгновенно разрядится. Это значит что с правой обкладки уйдет в провод избыток электронов, а из провода на левую обкладку войдет недостаток электронов. На обоих обкладках электронов будет одинаково, конденсатор разрядится.
До какого напряжения заряжается конденсатор?
Он заряжается до такого напряжения, которое к нему приложено с источника питания.
Сопротивление конденсатора.
Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.
Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.
Вся энергия затрачиваемая источником тока на преодоление емкостного
сопротивления превращается в энергию электрического поля конденсатора.
Когда конденсатор будет разряжаться вся энергия электрического поля
вернется обратно в цепь в виде энергии электрического тока. Таким
образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.
Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?
Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.
А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.
В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.
Одновременная поляризация огромного количества атомов образует ток, называемый током смещения. Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.
конденсатора определяется по формуле
Определение результирующего сопротивления конденсатора
Результирующее сопротивление конденсатора нельзя находить суммируя величины его активного и емкостного сопротивлений. Это делается по формуле
4.4. Зарядка конденсатора
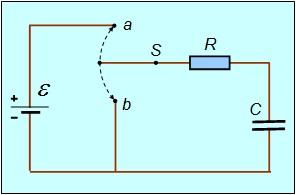
В этом разделе мы решим задачи о зарядке и разрядке конденсатора. Электрическая цепь показана на рис. 4.20. Переключатель S позволяет подсоединять и отсоединять источник тока.
Рис. 4.20. Цепь для зарядки и разрядки конденсатора
Пусть сначала конденсатор емкостью С не заряжен, и мы перебрасываем выключатель в положение а. По цепи пойдет зависящий от времени ток I(t), переносящий положительный заряд на верхнюю пластину конденсатора. Отметим, что хотя ток зарядки и разрядки конденсатора не является постоянным, но рассматривается здесь, поскольку его изменение в данном случае можно считать медленным. Обозначим заряд на этой пластине в момент t через q(t). Напряжение на конденсаторе можно найти как разницу между ЭДС и падением напряжения на нагрузке, то есть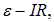 
либо как отношение заряда к емкости q/C. Приравнивая эти выражения, получаем первое уравнение процесса зарядки
Согласно закону сохранения заряда, изменение заряда q на обкладках конденсатора происходит только из-за наличия тока I. Поэтому второе уравнение процесса имеет вид
Подставим (4.37) в (4.36):
Мы видим, что у этого уравнения имеется стационарное решение (постоянный заряд на конденсаторе)
При таком заряде на конденсаторе напряжение на нем равно ЭДС источника тока, и ток по цепи не идет
Введем отклонение у заряда на конденсаторе от его стационарного значения
Подставляя это соотношение в (4.38), находим уравнение для функции y(t)
Это уравнение легко интегрируется
Вычисляя интегралы. находим
где y0 — произвольная постоянная интегрирования (значение у в начальный момент времени). Отсюда находим заряд на конденсаторе
Нам осталось использовать начальное условие: в момент t = 0 конденсатор был не заряжен
Дифференцируя q(t) по времени, находим ток в цепи
Напряжение на конденсаторе U(t) = q(t)/C без труда получается из (4.39)
Таким образом, по мере роста заряда и напряжения на конденсаторе ток в цепи уменьшается. При этом заряд конденсатора стремится к своему стационарному значению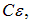 
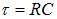
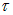
а напряжение на конденсаторе — к ЭДС источника тока. Величина 
имеет размерность времени и определяет характерное время процесса зарядки. За промежуток 
ток в цепи уменьшается
в е = 2,72 раза.
На рис. 4.21 показана зависимость заряда на конденсаторе и тока в цепи для конкретных значений R = 1,5 кОм, С = 2 мкФ,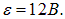 
Характерное время процесса равно при этих значениях 
Из рисунков видно, что уже при временах порядка
конденсатор почти полностью заряжается.
Рис. 4.21. Графики зависимости напряжения на конденсаторе (слева) и тока в цепи (справа)
при зарядке конденсатора емкостью С = 2 мкФ через активное сопротивление R = 1,5 кОм от источника тока с ЭДС 12 В
Рассмотрим теперь процесс разрядки конденсатора. Зарядив его до какого-то заряда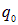 
(или, что то же самое, до начального напряжения U0 = q0/C), мы перебрасываем переключатель в положение b (см. рис. 4.20). Конденсатор начнет разряжаться, а по цепи пойдет ток. Мы имеем те же самые уравнения за исключением того, что в цепь не включен источник тока. Поэтому в этом случае надо положить 
в уравнении (4.38). Тогда оно совпадет с тем, что мы ранее решали для y(t), поэтому решения для процесса разрядки конденсатора нам уже известны
Все эти величины быстро уменьшаются с течением времени: за тот же характерный промежуток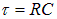 
заряд конденсатора, напряжение на нем и ток в цепи падают в 2,72 раза. Отрицательный знак в выражении для тока означает, что ток при разрядке течет в направлении, обратном току при зарядке конденсатора.
Дополнительная информация
Конденсатор
Конденсатор имеет следующее схематическое изображение
Рассмотрим водопроводную модель конденсатора. Ранее мы говорили о том, что ток может течь только в трубе, соединенной в кольцо в замкнутой цепи. Но можно представить пустую емкость, в которую можно заливать воду, пока емкость не заполнится. Это и есть конденсатор — емкость, в которую можно заливать заряд.
Если характеристикой резистора является сопротивление, то электрической характеристикой конденсатора является емкость.
Емкость говорит, сколько заряда можно в конденсатор закачать, чтобы напряжение там поднялось до величины U. Можно сказать, что емкость характеризует диаметр трубы. Чем ýже труба, тем быстрее поднимается уровень воды при закачке и растет давление на дне трубы. Давление же зависит только от высоты водяного столба, а не от массы закачанной воды.
В электрических терминах, чем меньше емкость конденсатора, тем быстрее растет напряжение при закачке туда заряда.
Рассмотрим теперь электрические цепи с конденсатором.
Пусть конденсатор подключен к генератору напряжения.
рис 9. Подключение конденсатора к генератору напряжения.
«Главный инженер повернул рубильник» S1 и.. тыдыщ. Что произошло?
Идеальный генератор напряжения имеет бесконечную мощность и может выдавать бесконечный ток. Когда замкнули рубильник в нашу емкость хлынуло бесконечное количество заряда в секунду и она мгновенно заполнилась и напряжение на ней выросло до U.
Теперь рассмотрим более реальную цепь.
Это Вторая Главная Цепь в жизни инженера-электронщика (после делителя напряжения) —
RC–цепочка.
RC–цепочка
RC–цепочка интегрирующего типа
Что произойдет в этой схеме, если замкнуть выключатель S1?
Конденсатор С исходно разряжен и напряжение на нем рано 0. Поэтому ток в первый момент будет равен I=U/R. Затем конденсатор начнет заряжаться, напряжение на нем увеличивается, и ток через резистор начнет уменьшаться. I=(U-Uc)/R. Этот процесс будет продолжаться, конденсатор будет заряжаться уменьшающимся током до напряжения источника U. Напряжение на конденсаторе при этом будет расти по экспоненте.
рис 11. График роста напряжения на конденсаторе при подаче напряжения величиной U (ступеньки).
Вопрос: А если запитать такую цепочку от генератора тока, как будет расти напряжение на конденсаторе?
Как выше было отмечено, ток в первый момент после подачи напряжение будет равен I=U/R, так как конденсатор разряжен, и напряжение на нем равно 0. И какое-то время, пока напряжение на конденсаторе Uc мало по сравнению с U, ток будет оставаться почти постоянным. А при заряде конденсатора постоянным током напряжение на нем растет линейно.
Uc=Q/C, а мы помним, что ток это количество заряда в секунду, то есть скорость протекания заряда. Другими словами, заряд это интеграл от тока.
Q = ∫ I * dt =∫ U/R * dt
Uc=1/RC * ∫ U * dt
Но все это близко к истине в начальный момент, пока напряжение на конденсаторе малó.
На самом деле все сводится к тому, что конденсатор заряжается постоянным током.
А постоянный ток выдает генератор тока. (См. вопрос выше)
Если источник напряжения выдает бесконечно большое напряжение и сопротивление R также имеет бесконечно большую величину, то по факту мы имеем уже идеальный генератор тока, и внешние цепи на величину этого тока влияния не оказывают.
RC–цепочка дифференцирующего типа
Ну тут все то же самое, что в интегрирующей цепочке, только наоборот.
рис 12. Дифференцирующая цепочка.
Более подробно свойства RC цепей хорошо освещены в интернете.
Параллельное и последовательное соединение конденсаторов
Так же как резисторы, конденсаторы можно соединять последовательно и параллельно.
Накачка и сброс — больше энергии, чем вы ожидали!
В статье рассмотрен метод заряда блока конденсаторов для накопления энергии, обеспечивающий достаточный запас мощности для питания всех типов нагрузок. Описана схема обратноходового преобразователя с высокой выходной мощностью, использованного для заряда блока суперконденсаторов. Статья представляет собой перевод [1].
Разработчики часто сталкиваются с трудностями при создании высокоэффективных преобразователей мощности. Причина — необходимость уменьшить тепловыделение в ограниченной области, чтобы обеспечить другие подсистемы большей входной мощностью или сберечь электроэнергию из соображений экологичности. Что же должен сделать разработчик, когда от него требуется обеспечить выходную мощность, превосходящую входную мощность на 50 или 100%? Эта на первый взгляд невыполнимая задача может быть решена, хотя и с некоторыми ограничениями. Некоторые виды нагрузки требуют большие мощности лишь в относительно короткие периоды времени продолжительностью в миллисекунды, секунды или даже минуты. В статье рассматривается, как этого можно добиться, заряжая блок конденсаторов для накопления энергии (накачка), пока она не потребуется, и разряжая конденсаторы на нагрузку контролируемым образом (сброс).
Все источники подводимого электропитания имеют ограниченные предельные значения тока, напряжения или мощности. Из-за наличия внутреннего сопротивления выходное напряжение батарей падает при большой нагрузке, тем самым косвенно устанавливая наибольший выходной ток для стабилизации напряжения на нагрузке. Практически все адаптеры питания рассчитаны на наибольший уровень выходной мощности. При превышении этого уровня адаптер питания может перейти в режим защиты от перегрузки по току, либо может даже сработать предохранитель для защиты источника входного питания. Интерфейс USB используется как источник питания с напряжением 5 В с выходным током всего 0,1A, но при необходимости может обеспечивать максимальный выходной ток до 0,5 A. Такая величина тока ограничивает мощность этого чрезвычайно распространенного источника питания величиной всего 2,5 Вт. Дополнительную выходную мощность можно получить только от источника накопленной энергии, например от конденсатора или батареи.
Передача тока в нагрузку от заряженного конденсатора определяется переносом требуемого количества заряда в течение определенного периода времени. В терминах подводимой мощности этот процесс можно определить с помощью уравнения:
где Cbulk — емкость заряжаемого конденсатора; Vi — начальное напряжение конденсатора, а Vf — конечное напряжение после разряда.
Эта концепция проста в реализации: следует зарядить конденсатор большой емкости до начального высокого напряжения и дать ему разрядиться до заданного уровня; при этом ток подается в нагрузку в условиях временной перегрузки по току. В конце цикла разряда на конденсаторе останется напряжение Vf, и потребуется повторный заряд конденсатора до напряжения Vi. Мощность, которую должен поддерживать конденсатор большой емкости, равна подводимой к нагрузке мощности за вычетом мощности, которая обеспечивается входным источником питания во время разряда. При расчете КПД всех импульсных преобразователей не следует занижать требуемую величину емкости конденсатора. Уравнение (1) представляет собой выражение для напряжения на конденсаторе при подаче постоянной мощности на нагрузку. Однако это является наихудшей ситуацией, поскольку не всякая нагрузка требует постоянной мощности.
Примером нагрузки постоянной мощности служит вход регулируемого импульсного источника питания. Для поддержания постоянной мощности по мере уменьшения входного напряжения импульсного источника питания входной ток должен возрастать. Нагрузка может быть резистивной или проявлять себя как источник постоянного тока. На рисунке 1 показаны разрядные характеристики трех типов нагрузки. Все характеристики начинаются в одной точке, соответствующей начальному напряжению, но затем они расходятся. Ток постоянного сопротивления изменяется противоположно току постоянной мощности и снижается при уменьшении напряжения, постепенно стабилизируясь по мере разряда. Разряд на нагрузку в режиме постоянного тока происходит линейно до нулевого напряжения, причем обеспечивается одинаковый ток, независимо от напряжения на конденсаторе. Разряд в режиме постоянной мощности, в свою очередь, происходит быстрее всего из-за резкого возрастания разрядного тока по мере уменьшения напряжения. В зависимости от типа нагрузки необходимая емкость может существенно изменяться, поэтому всегда полезно знать характер конкретной нагрузки.
При использовании блока конденсаторов разработчик должен также решить, до каких пределов его можно будет разряжать. Существуют два возможных способа. Первый состоит в непосредственном подключении нагрузки к блоку конденсаторов. Перепад напряжения на конденсаторах должен находиться в допустимых для нагрузки эксплуатационных пределах. Обычная полупроводниковая нагрузка допускает отклонение лишь 3—5% от номинального напряжения. Это существенно ограничивает допустимое падение напряжения и принуждает использовать конденсаторы большой емкости. В этом случае не требуется дополнительной стабилизации напряжения.
Второй способ допускает большие перепады напряжения и использует дополнительный стабилизатор между конденсатором и нагрузкой. Стабилизатор может быть понижающим, повышающим или даже SEPIC-преобразователем, в зависимости от размаха напряжения на входе, выходе и конденсаторе. При большом перепаде напряжения на конденсаторе более эффективно используется запасенная энергия, что минимизирует величину необходимой емкости. Уменьшение требуемой емкости может снизить общие затраты, даже с учетом расходов на дополнительный стабилизатор.
Преимущество суперконденсаторов — плотность энергии, которая в 1000—10000 раз превышает плотность энергии электролитических конденсаторов. В настоящее время часто используются конденсаторы с номинальным значением емкости 100 Ф и более. Многие из них предназначены для приложений с малым потреблением тока, например для резервных запоминающих устройств. Конденсаторы таблеточного типа часто имеют эквивалентное последовательное сопротивление (equivalent series resistance — ESR) 100 Ом и более. Разработчик должен определить максимальное допустимое ESR исходя из разрядного тока и падения напряжения. Современные типы суперконденсаторов имеют очень малую величину ESR, сравнимую с аналогичным показателем для керамических конденсаторов.
На схеме, представленной на рисунке 2, были выбраны суперконденсаторы с малым ESR, поскольку они должны служить источником тока в сотни миллиампер. Питание схемы осуществляется от порта USB с предельным значением входной мощности 2,5 Вт. Выходное напряжение преобразователя составляет 7 В на импульсной нагрузке 4,2 Вт в течение 4 с, а затем 0,7 Вт в течение 15 с. Изолированный обратноходовой преобразователь с контроллером TPS40210 использован для заряда блока суперконденсаторов до напряжения 13,5 В во время режима малой нагрузки. Допускается разряд конденсатора приблизительно до 9,5 В через 4 с режима большой нагрузки. В течение этого периода входной ток стабилизируется на уровне не более 0,5 A (2,5 Вт) и измеряется резистором с помощью операционного усилителя. Если величина входного тока стремится превысить 0,5 A, эта токовая петля управляется напряжением вторичного контура. Во время регулирования входного тока входная мощность продолжает подаваться на вторичный контур, но ограничена уровнем 2,5 Вт, тогда как дополнительная мощность подается на нагрузку блоком конденсаторов.
На рисунке 3 показаны графики изменения тока и напряжения. Во время импульса тока нагрузки 0,6 А (нижняя кривая) напряжение на суперконденсаторе (верхняя кривая) снижается приблизительно до 4 В. Это значение является входным напряжением для синхронного понижающего DC/DC-преобразователя типа TPS62110, стабилизирующего выходное напряжение на уровне 7 В (средний сигнал). Когда выходной ток нагрузки при напряжении 7 В уменьшается до 0,1 A, блок конденсаторов повторно полностью заряжается до 13,5 В. Во время этих ступенчатых изменений режимов нагрузки и больших перепадов входного напряжения выходное напряжение остается стабильным с небольшими отклонениями.
На рисунке 4 показаны сигналы в момент подачи напряжения 4,5 В на вход USB. При включении блок конденсаторов первоначально разряжен, а обратноходовой преобразователь немедленно переключается в режим ограничения входного тока, поскольку выходная нагрузка ведет себя как короткозамкнутая. Блок конденсаторов медленно заряжается до напряжения 13,5 В со скоростью, которая определяется ограничением по входной мощности 2,5 Вт и потерями, связанными с КПД обратноходового преобразователя. Когда напряжение достигает 13,5 В, вторичный контур принимает управление на себя, позволяя уменьшить входной ток. В этом примере выходная нагрузка отсутствует, хотя для полного заряда конденсаторов требуется приблизительно 18 с. Время запуска будет еще более продолжительным, если подключить внешнюю нагрузку. Это является одним из недостатков, связанных с наличием накопительного конденсатора большой емкости.
Схема, представленная в этой статье, обеспечивает построение изолированного источника питания, мощность которого больше мощности входного источника питания. Хранение энергии в конденсаторе большой емкости имеет свои недостатки, в частности, высокую стоимость суперконденсаторов и продолжительное время запуска. Тип нагрузки непосредственно влияет на величину необходимой емкости для длительной поддержки требуемой величины напряжения. Нагрузка с постоянной мощностью, например такая как стабилизирующий импульсный преобразователь, представляет собой наиболее тяжелый вид нагрузки и может разрядить накопительный конденсатор быстрее, чем резистивная нагрузка или нагрузка по постоянному току. Однако если в схеме предусмотреть возможность значительного снижения напряжения на накопительном конденсаторе, после которого включен импульсный стабилизатор, то можно удовлетворить потребности в энергии для самой большой нагрузки.