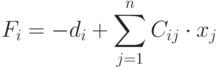если на каком либо шаге не удается отыскать ненулевой ведущий элемент то это значит

Компьютерное моделирование и решение линейных и нелинейных многомерных систем

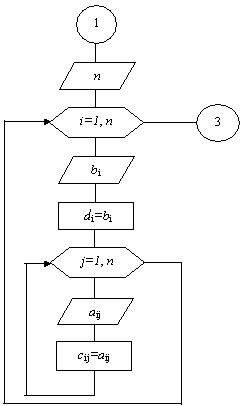
Блок 2. С помощью двух вложенных циклов с управляющими переменными i=1,n и j=1,k организуем ввод коэффициентов a_i,j и свободных членов b_i исходной системы. Для того, чтобы в дальнейшем можно было выполнить в блоке 9 проверку результата, в алгоритме предусмотрено сохранение значений a_i,j и b_i исходной системы с помощью переприсвоений: c_ij=a_ij и d_i=b_i

Блок 4. На каждом шаге прямого хода выполняем поиск ненулевого ведущего элемента.

Поиск ненулевого ведущего элемента ведётся в следующем порядке:

а) На каждом k-ом шаге прямого хода ведущий элемент каждой строки сравнивается с нулём;

б) Если в k-ой строке имеется нулевой ведущий элемент, то в k-ом столбце в цикле осуществляется поиск ненулевого элемента.

г) Если ненулевой ведущий элемент не найден, то коду ошибки kо присваиваем значение 1 и расчёт прекращается.

Если корни системы найдены, то F_i – это число, близкое к нулю.

Блок 9 в алгоритме метода Гаусса рекомендуется использовать только в процессе отладки метода.

В дальнейшем, при использовании метода Гаусса при решении различных прикладных задач, особенно в тех случаях, когда метод Гаусса используется внутри другого метода, блок 9 можно опустить, а в блоке 2 при вводе данных исходные значения коэффициентов системы и её свободных членов можно не сохранять.

Источник

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m

Источник

Метод Гаусса-Жордана. Примеры решения систем линейных алгебраических уравнений методом Гаусса-Жордана.

Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса. Нередко этот метод называют методом Жордана или Жордана-Гаусса.

В данном методе решения СЛАУ мы работаем с расширенной матрицей системы. Преобразования, допустимые в методе Гаусса-Жордана те же, что и в методе Гаусса:

Впрочем, обязательным условием оставим лишь вычёркивание нулевых строк. Из повторяющихся или пропорциональных строк в любом случае останется лишь одна, а остальные позже станут нулевыми и будут удалены из матрицы.

Перед тем, как рассмотреть преобразования метода Гаусса-Жордана, введём несколько терминов.

Описание алгоритма с произвольным выбором разрешающего элемента

Далее выполняем действия со строками, чтобы обнулить все ненулевые элементы j-го столбца, кроме разрешающего элемента. После этого переходим к следующему столбцу. При этом из каждой строки можно взять разрешающий элемент лишь один раз.

Нулевые строки вычёркиваются по мере их появления. Если разрешающий элемент станет выбрать невозможно, алгоритм прекращается. Данным методом решены примеры №1 и №2 на этой странице.

Более развёрнутое пояснение этого метода дано в примечании ниже.

Подробное описание метода: показать\скрыть

На втором шаге переходим к следующему столбцу матрицы системы. Посмотрим, нет ли в этом столбце элемента, не равного нулю, при этом не принадлежащего строке, из которой был выбран разрешающий элемент на предыдущем шаге. Если такого разрешающего элемента во втором столбце нет, то переходим к третьему, четвёртому столбцу и так далее – до тех пор, пока либо не найдём столбец, в котором будет нужный нам элемент, либо убедимся, что искомый столбец в матрице системы отсутствует (это будет означать окончание алгоритма).

Описание алгоритма с последовательным перебором строк

Если предыдущий вариант алгоритма предполагал последовательный перебор столбцов, то в данном случае мы будем осуществлять последовательный перебор строк. На каждом шаге этого варианта метода Гаусса-Жордана используется некая строка расширенной матрицы системы. На первом шаге применяется первая строка, на втором шаге – вторая и так далее. Замечание про нулевые и повторяющиеся строки, сделанное выше, остаётся в силе. Нулевые строки вычёркиваем по мере их появления.

Расширенная матрица системы будет такой:

На каждом шаге метода Гаусса-Жордана нам придётся выбирать некие ненулевые элементы матрицы системы (разрешающие элементы). Выбирать можно по-разному, и в зависимости от выбора разрешающих элементов будет отличаться процесс решения. В этом примере мы станем выбирать разрешающий элемент произвольно.

Обратимся к первому столбцу матрицы системы (матрица системы записана до черты). Надо выбрать в первом столбце какой-либо ненулевой элемент, который и будет разрешающим элементом.

Заметьте, что вторую строку эти преобразования не затрагивают, поэтому в новую матрицу вторая строка перейдёт без изменений.

Разумеется, самым удачным выбором будет 1. На первом шаге, чтобы разрешающим элементом стала единица, мы делили вторую строку на 2. Здесь эта операция не нужна, так как разрешающий элемент уже равен 1. С помощью разрешающего элемента (он выделен красным) мы обнулим два остальных ненулевых элемента второго столбца, выделенных синим цветом:

Второй шаг окончен. Все «синие элементы» обнулены. Переходим к третьему шагу.

Выбрать разрешающий элемент в следующем столбце матрицы системы невозможно, так как матрица системы содержит всего три столбца. Решение окончено, ответ получен.

Как получились значения переменных? показать\скрыть

Давайте перейдём от последней полученной нами матрице к системе:

Упрощая полученную систему, имеем:

Полное решение без пояснений выглядит так:

Разумным будет выбор единицы из четвёртой строки в качестве разрешающего элемента во втором столбце. Однако если есть необходимость взять разрешающий элемент из иной строки, то можно просто поменять строки местами. Например, если мы хотим, чтобы разрешающий элемент принадлежал второй строке, поступим так:

Выполнять описанные выше вспомогательные действия или нет – надо смотреть по ситуации. Если действий с дробями предвидится немного, то особого смысла в попытках их избежать нет. Если же нас ожидают ещё несколько шагов метода Гаусса-Жордана, то, разумеется, лучше упростить себе расчёты и выполнить некое дополнительное действие, чтобы потом не работать с дробями.

Расширенная матрица системы будет такой:

В этом примере мы, как и в предыдущем примере №1, станем выбирать разрешающий элемент произвольно.

Обратимся к первому столбцу матрицы системы. Надо выбрать в первом столбце какой-либо ненулевой элемент, который и будет разрешающим элементом.

На последней матрице мы убрали нулевую строку. Решение окончено, так как в следующем столбце разрешающий элемент выбрать уже невозможно – все строки использованы.

Обратите внимание на столбцы, которые содержат по одному ведущему элементу некоей строки. Это столбец №1 (он содержит ведущий элемент строки №3), столбец №3 (он содержит ведущий элемент строки №2) и столбец №4 (он содержит ведущий элемент строки №1). Эти столбцы для наглядности я выделил синим цветом:

Полное решение без пояснений таково:

Этот пример станем решать с помощью последовательного перебора строк. Для начала запишем расширенную матрицу данной системы:

Этот пример станем решать с помощью последовательного перебора строк. Для начала запишем расширенную матрицу данной системы:

Теперь пора обнулять все ненулевые элементы третьего столбца, расположенные ниже и выше второй строки, однако эти элементы и так равны нулю. Следовательно, просто переходим к следующему шагу.

В принципе, нам ничто не мешает выполнить эти преобразования. Однако работать с дробями не очень хочется. Чтобы избежать работы с дробями можно поменять местами текущую третью строку с одной из нижележащих строк – с четвёртой строкой. Если мы это сделаем, то разрешающим элементом станет единица, что означает отсутствие необходимости работать с дробями. После смены строк выполним обнуление требуемых элементов:

На четвёртом шаге используем четвёртую строку. Аналогично предыдущим шагам, получим:

Данный пример я не буду расписывать с подробными пояснениями, так как они были даны ранее. Решать станем с помощью последовательного перебора строк.

Впрочем, к этому же выводу можно прийти, записав ранги матрицы системы и расширенной матрицы системы. Вычеркнем нулевую строку:

Ответ: система несовместна.

Исследовать на совместность СЛАУ

Найти её решение методом Гаусса-Жордана.

Источник

Теоретико-числовые методы в криптографии (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Тогда решение сравнения по модулю 125 есть x=±(6+25(1+5t3))=±(31+125t3).

Рассмотрим теперь сравнение вида x2≡a(mod 2α). Такое сравнение не всегда имеет два решения. Для такого модуля возможны случаи:

1) α=1. Тогда сравнение имеет решение только тогда, когда a≡1(mod 2), и решением будет x≡1(mod 2) (одно решение).

2) α=2. Сравнение имеет решения только тогда, когда a≡1(mod 4), и решением будет x≡±1(mod 4) (два решения).

3) α≥3. Сравнение имеет решения только тогда, когда a≡1(mod 8), и таких решений будет четыре. Сравнение x2≡a(mod 2α) при α≥3 решается так же, как сравнения вида x2≡a(mod pα), только в качестве начального решения выступают решения по модулю 8: x≡±1(mod 8) и x≡±3(mod 8). Их следует подставить в сравнение по модулю 16, затем по модулю 32 и т. д. вплоть до модуля 2α.

Решить сравнение x2≡33(mod 64)

64=26. Проверим, имеет ли исходное сравнение решения. 33≡1(mod 8), значит сравнение имеет 4 решения.

По модулю 8 эти решения будут: x≡±1(mod 8) и x≡±3(mod 8), что можно представить как x=±(1+4t1). Подставим это выражение в сравнение по модулю 16

Тогда решение примет вид x=±(1+4t1)=±(1+4(0+2t2))=±(1+8t2). Подставим получившееся решение в сравнение по модулю 32:

Тогда решение примет вид x=±(1+8t2) =±(1+8(0+2t3)) =±(1+16t3). Подставим получившееся решение в сравнение по модулю 64:

Тогда решение примет вид x=±(1+16t3) =±(1+16(1+2t4)) =±(17+32t4). Итак, по модулю 64 исходное сравнение имеет четыре решения: x≡±17(mod 64) и x≡±49(mod 64).

Теперь рассмотрим сравнение общего вида: x2≡a(mod m), (a,m)=1, — каноническое разложение модуля m. Согласно Теореме из п.4 §4, данному сравнению равносильна система

Если каждое сравнение этой системы разрешимо, то разрешима и вся система. Найдя решение каждого сравнения этой системы, мы получим систему сравнений первой степени, решив которую по китайской теореме об остатках, получим решение исходного сравнения. При этом количество различных решений исходного сравнения (если оно разрешимо) есть 2k, если α=1, 2k+1, если α=2, 2k+2, если α≥3.

Решить сравнение x2≡4(mod 21).

21 – составное число. Факторизуем его: 21=3·7. Проверим разрешимость исходного сравнения:

, . Сравнение разрешимо и имеет 22=4 решения.

Составим систему: . Решим каждое из уравнений этой системы. Получим . Итак, имеем 4 системы:

1) 2) 3) 4)

Решая каждую из этих систем по китайской теореме об остатках, получим четыре решения: x≡±2(mod 21), x≡±5(mod 21).

5.6. Тест на простоту Миллера-Рабина.

Теперь, наконец, мы располагаем достаточной информацией для того, чтобы привести тест Миллера-Рабина. Этот тест, как и тесты Ферма и Соловея-Штрассена, строит вероятно простые числа, то есть число, опознанное этим тестом как простое, может с некоторой малой вероятностью оказаться составным, однако вероятность ошибки у теста Миллера-Рабина гораздо ниже, чем у первых двух тестов. Как правило, для опознания простого числа достаточно одной итерации теста, но все же рекомендуемое количество итераций – пять.

Тест Миллера-Рабина основан на двух важных фактах:

Докажем несколько важных теорем, описывающих свойства Om(a):

2: 20=1, 21=2, 22=4, 23=8, 24=5, 25=10, 26=9, 27=7, 28=3, 29=6, 210=1. O11(2)=10.

3: 30=1, 31=3, 32=9, 33=5, 34=4, 35=1. O11(3)=5.

4: 40=1, 41=4, 42=5, 43=9, 44=3, 45=1. O11(4)=5.

5: 50=1, 51=5, 52=3, 53=4, 54=9, 55=1. O11(5)=5.

6: 60=1, 61=6, 62=3, 63=7, 64=9, 65=10, 66=5, 67=8, 68=4, 69=2, 610=1. O11(6)=10.

7: 70=1, 71=7, 72=5, 73=2, 74=3, 75=10, 76=4, 77=6, 78=9, 79=8, 710=1. O11(7)=10.

8: 80=1, 81=8, 82=9, 83=6, 84=4, 85=10, 86=3, 87=2, 88=5, 89=7, 810=1. O11(8)=10.

9: 90=1, 91=9, 92=4, 93=3, 94=5, 95=1. O11(9)=5.

10: 100=1, 101=10, 102=1. O11(10)=2.

Действительно, порядки всех элементов делят порядок группы. При этом в группе U11 нашлись порождающие элементы, причем не один, а четыре. Это 2, 6, 7 и 8. Однако не во всех группах Um существуют порождающие элементы, убедимся в этом на следующем примере:

3: 30=1, 31=3, 32=1. O8(3)=2.

5: 50=1, 51=5, 52=1. O8(5)=2.

7: 70=1, 71=7, 72=1. O8(7)=2.

Итак, в группе U8 нет порождающего элемента.

Возникает вопрос – в каких группах Um порождающий элемент существует, а в каких – нет, и как найти порождающий элемент? На этот вопрос ответим в следующих пунктах данного параграфа.

6.2. Существование первообразных корней по модулю p.

Om(x)=abOm(xa)=b.

Om(x)=a, Om(y)=b, (a,b)=1 Om(xy)=ab.

Доказательства этих лемм не представляют принципиальной сложности, поэтому предоставляются читателю в качестве упражнения.

Теорема 1 (Критерий Люка).

Тогда, согласно Лемме 1, Op(η)=, где η=.

Согласно Лемме 2, Op(g)=τ=, где g=η1η2…ηk.

Поэтому, согласно Теореме 3, п.1, τ\(p—1).

6.3. Первообразные корни по модулям pα, 2pα.

Пусть g – первообразный корень по модулю p, тогда существуют такое число t, что u= не делится на p, и тогда g+pt – первообразный корень по модулю pα α>1.

Число u, заданное условием, является целым в силу теоремы Ферма. Действительно, поскольку gUp, то (g,p)=1 (g+pt,p)=1по теореме Ферма, (g+pt)p—1≡1(mod p) p\((g+pt)p—1 –1).

где если t пробегает Zp, то и u пробегает Zp (полную систему вычетов по модулю р). Поэтому существует такое tZp, для которого u не делится на p. При таком t из (*) получаем:

где все ui, i=2,3,…α—1 не делятся на р.

Но (*) и (**) показывают, что сравнение верно при r = α и неверно при r —1, то, если для некоторого a будут выполнены условия Теоремы Поклингтона (1) и (2), то n – простое.

Таким образом, можно значительно сократить количество проверок по сравнению с тестом Миллера.

=an—m—an—2m+…+a3m—a2m+am—a0 Z.

Тогда (am+1)\(an+1), значит p – составное число. Предположение неверно, следовательно верно обратное.

Числа Fk=+1 называются числами Ферма.

F0=3, F1=5, F2=17, F3=257, F4=65739 – простые числа. Пьер Ферма выдвигал гипотезу о простоте всех чисел Ферма, но Леонардом Эйлером в 1732 г. была показана составность числа F5.

В настоящее время существует следующий критерий проверки чисел Ферма на простоту:

Fk – простое число .

Пусть Fk – простое число. Тогда по критерию Эйлера для символа Лежандра,

.

В силу простоты, Fk не делится на 3.

Поэтому возможны два случая: Fkmod 3=1 или Fk mod 3=2.

Случай Fk mod 3=1 невозможен, так как это значило бы, что mod 3 = 0, а это не так. Поэтому Fk mod 3=2, и тогда

На основании теоремы Пепина построен тест Пепина, проверяющий верность сравнения . Тест Пепина детерминированный, состоит из одной итерации и дает точный ответ о простоте или составности числа Ферма.

7.4. Числа Мерсенна.

Если число вида p=an—1 – простое 1) a – четное;

Четность а очевидна, так как иначе р было бы четным, а значит, составным.

Допустим, что n – не простое n=mk. Тогда

=ak(m—1)+ak(m—2)+…+ak+1Z.

Тогда (ak—1)\(an—1), значит р – не простое число. Предположение неверно, значит верно обратное.

Простые числа вида Mp=2p—1, где р – простое число, называются числами Мерсенна.

Число вида Mp=2p—1, где р>2 – простое число, является простым в последовательности, определенной равенствами u0=4, ui+1=(ui2—2) mod Mp, выполняется up—2≡0(mod Mp).

Из Теорем 1 и 2 следует

Тест Лукаса-Лемера для чисел Мерсенна

Вход: Число Мерсенна Mn=2n—1.

Ш.1. Пробными делениями проверить, имеет ли n делители между «2» и . Если имеет, идти на Выход с сообщением «Mn – составное число».

Ш.4. Если u=0, то «Mn – простое число», иначе «Mn – составное число».

В настоящее время особое внимание уделяется двойным числам Мерсенна MMp=2Mp –1, например 7=M3=MM2. Алгоритм построения таких чисел следующий: сначала строится сравнительно небольшое простое число Мерсенна Mp, а затем по нему – двойное число Мерсенна MMp, которое проверяется на простоту тестом Лукаса-Лемера минуя первый шаг.

Аналогично строятся тройные и т. д. числа Мерсенна. Например, тройным числом Мерсенна является 127=M7=MMM2.

Не для всех чисел Мерсенна существуют двойные и тройные числа. Например, MM13 не является простым.

Первыми простыми числами Мерсенна являются M2=3, M3=7, M5=31, M7=127, M13=8191, M17, M19, M31.

На данный момент (2007 г.) не доказана конечность или бесконечность количества простых чисел Мерсенна.

7.5. Теорема Диемитко и процедура генерации простых чисел заданной длины ГОСТ Р 34.10-94.

Следующая теорема позволяет строить доказуемо простые числа большего размера на основе простых чисел меньшего размера.

Пусть n=qR+1, где q – простое число, R – четное, R 2t, возвращаемся на Ш.1.

Ш.5. Если 2n—1≡1(mod n) и 2N+u1(mod n), то идем на Выход.

Ш.6. Вычисляем u=u+2. Возвращаемся на Ш.3.

Выход. p – простое число.

Первое слагаемое в построении числа N обеспечивает минимальный требуемый размер числа p, а второе вносит в процедуру поиска новых простых чисел необходимый элемент случайности.

Проверка на Шаге 4 необходима, чтобы число p не превышало своей верхней границы, а проверка на Шаге 5 есть проверка условия теоремы Диемитко при a=2.

1. N==3. N=N+1=4.

4. 13 1 кольцо Mn(K) всегда некоммутативное.

Пример 10. Рассмотрим множество остатков (вычетов)

Zn=<0,1,2,…, n—1> от деления на натуральное число n. Введем на нем операции сложения и умножения

,

где a+b и ab обозначают обычные сложение и умножение целых чисел.

Относительно введенных операций множество Zn является коммутативным кольцом с единицей.

Самое маленькое кольцо, и самое любимое программистами, это кольцо Z2 = <0,1>вычетов по модулю 2. В дальнейшем мы не будем использовать обозначения Å, Ä, а пользоваться привычной плюсом и точкой.

И завершим наше короткое алгебраическое введение определением поля.

Определение. Коммутативное кольцо с единицей, в котором все ненулевые элементы имеют обратный по умножению, называется полем.

Пример 11. Множество Q рациональных чисел с обычными операциями сложения и умножения является полем.

Множество R действительных чисел с обычными операциями сложения и умножения является полем.

Проверить, что кольцо многочленов K[x] не является полем. (Подсказка. Какой многочлен является обратным к многочлену х2 по умножению?).

Проверить, что кольцо матриц Mn(K) при n>1 не является полем.

1.2. Делимость в кольцах.

Неформально говоря, в полугруппе можно только умножать (или прибавлять). В группе можно умножать и делить (или прибавлять и вычитать). В кольце можно прибавлять, вычитать и умножать. В поле можно прибавлять и вычитать, умножать и делить.

Когда в поле рациональных чисел мы говорим, что «делим число 2 на число 3», то это является вольным изложением более правильного выражения «умножаем число 2 на число обратное по умножению к числу 3». Почему нельзя делить на 0? Поскольку, 0a=0, то 0 не имеет обратного по умножению и поэтому делить не на что.

В то же время, в кольце целых чисел, хотя число 3 и не имеет обратного по умножению, число 3 делит число 6. И здесь понятие делимости имеет уже несколько иной смысл, чем в предыдущем абзаце.

Определение. Элемент а кольца К делит элемент b кольца K, если существует элемент c кольца K, такой что b=ac. Точнее делит слева, т. к. кольцо может быть некоммутативным. Если b=ca, то а делит элемент b справа.

Обратим внимание, что в этом определении наличие обратного элемента у элемента «а» не предполагается.

Поскольку 0a=0, то по этому определению получается, что 0 делит 0. Получается лингвистическое противоречие. Ноль делит ноль, но ноль на ноль не делится!

В дальнейшем мы будем иметь дело только с коммутативными кольцами, то правую и левую делимость мы различать не будем. Если элемент a делит элемент b, то это обозначается a/b.

Свойства делимости. Пусть К – кольцо, a,b,c – его элементы.

4. Последнее свойство следует из свойств 1 и 2.

Третье свойство обычно называют транзитивностью. Кроме транзитивности среди свойств бинарных отношений, а делимость – это бинарное отношение, популярны рефлексивность и симметричность.

Чтобы выяснить, когда эти свойства имеют место, нам потребуется еще ряд определений.

Определение. Элемент a кольца К называется обратимым (или единицей), если существует элемент b, принадлежащий кольцу К, такой что, ab=1, где 1 – нейтральный элемент по умножению.

Множество К* обратимых элементов кольца К является группой относительно операции умножения.

Определение. Элемент a≠0 кольца К называется делителем нуля, если существует элемент b≠0 кольца К, такой, что ab=0.

Упражнение. Проверить, что кольца вычетов по составному модулю и кольца матриц Mn(K), при n >1, имеют делители нуля.

Благодаря тому печальному для потребителей обстоятельству, что кольца матриц имеют делители нуля, многие математики имеют работу. Причина в том, что решение систем линейных уравнений над кольцами с делителями нуля очень хлопотное дело и каждое кольцо требует отдельного исследования.

Рассмотрим кольцо Z8 и два уравнения с коэффициентами в этом кольце: 4x=0 и x2+x+1=0. Как легко проверить первое уравнение имеет четыре решения – 0, 2, 4, 6, а второе ни одного. □

Определение. Элементы a и b кольца К называются ассоциированными, если a\b и b\a.

Исследуем подробнее ассоциированные элементы. Если a\b и b\a, то одновременно выполняются два равенства b=ab1, a=ba1. Следовательно, . Таким образом, b(1—a1b1) = 0, и a(1—b1a1)=0. Если кольцо К не имеет делителей нуля, то получается, что

a1b1=1. То есть ассоциированные элементы отличаются друг от друга на обратимый элемент. Например, в кольце целых чисел группа обратимых элементов состоит из двух элементов Z*=<1, —1>, поэтому ассоциированными элементами будут, например, 3 и —3, 5 и —5.

Фундаментальную роль в алгебре и теории чисел, а также в криптографии, играют простые элементы кольца. В случае кольца целых чисел – простые числа.

Определение. Элемент p кольца К без делителей нуля называется простым, если он делится только на обратимые элементы и на ассоциированные с ним.

Если ограничится только натуральными числами, то определение простого элемента будет звучать так: «простой элемент делится только на себя и на единицу», поскольку среди натуральных чисел обратимым элементом является только 1.

У колец без делителей нуля есть одного замечательное свойство.

Основное свойство колец без делителей нуля.

Пусть К – кольцо без делителей нуля и a≠0, тогда из равенства ab=ac следует, что b=c.

Обратим внимание, что данное свойство означает логическое сокращение, а не умножение на элемент, обратный к элементу «а». Кстати, такого обратного может и не существовать.

1.3. Деление с остатком.

Помните фильм про Буратино и знаменитый диалог Лисы Алисы и Кота Базилио: “Пять на два не делится! Вот тебе, Базилио, один золотой, а вторую неделящуюся половину я забираю себе!” Кот ничего не понял, но почувствовал, что его обманывают.

Что означает «делится», мы выше видели, это когда есть дополнительный множитель и он восстанавливает равенство. А если множителя нет. Тут мы вступаем на зыбкую почву приближений.

При делении целых чисел и многочленов разные числа и многочлены можно легко сравнивать. У чисел сравнение ведется путем сравнения их модулей, а у многочленов – сравнением их степеней. Поэтому при неполном делении стремятся, что бы степень остатка была меньше, чем степень делителя.

Формально понятие степени можно ввести так.

Определение. Пусть К – кольцо без делителей нуля. Степенью элементов кольца К называется отображение ненулевых элементов кольца во множество натуральных чисел такое, что выполняется условие монотонности: Другими словами, степень произведения не меньше степени сомножителя. (Обратим внимание, что для нуля степень не определена!)

Если определено понятие степени элемента, то можно говорить о делении с остатком.

Определение Кольцо К называется кольцом с алгоритмом деления с остатком или евклидовым, если или r=0.

Евклидовых колец не очень много. Нас же будут в основном интересовать два из них.

Кольцо целых чисел Z является евклидовым, при этом степенью целого числа является его модуль. Алгоритм деления с остатком в кольце целых чисел изучался в школе.

Пусть P – поле, тогда кольцо многочленов P[x] является евклидовым, при этом степенью является обычная степень многочлена. Алгоритм деления с остатком – обычное деление многочленов уголком.

Сейчас мы докажем самую полезную теорему о евклидовых кольцах, которая применяется чуть не всей классической алгебре и криптографии.

Но прежде введем понятие наибольшего общего делителя (НОД) и двойственное ему наименьше обще кранное (НОК).

Определение. Элемент d=НОД(a,b) называется наибольшим общим делителем элементов a и b, если выполняются два условия:

Понятие наименьшего общего кратного НОК не так важно как НОД, но его введение поучительно в силу свой двойственности к НОД. «Наибольший» заменяется на «наименьший», «делится» на «делит».

Определение. Элемент m=НОК(a,b) называется наименьшим общим кратным элементов a и b, если выполняются два условия:

Фундаментальный факт состоит в том, что в евклидовых кольцах, а значит в кольце целых чисел и кольце многочленов над полем, – НОД существует и его можно выразить через исходные элементы.

Теорема (Основная теорем о евклидовых кольцах).

Пусть К – евклидово кольцо, тогда любые элементы имеют наибольший общий делитель и, более того, такие, что d=НОД(a,b)=au +bv.

а) Применяя свойство деления с остатком получим табличку уменьшающихся остатков. Так как степень каждого остатка – натуральное число, а натуральные числа не могут убывать бесконечно, то табличка будет конечной, а последний остаток нулевым.

В нашей табличке получилось n+2 строки. Какой же из участвующих в ней элементов является долгожданным НОД? Это последний ненулевой остаток rn. Для того, чтобы убедиться, что d=rn, нужно проверить оба свойства НОД. Прежде всего, просматривая табличку снизу вверх, убеждаемся, что rn делит a и b. В самом деле, последняя строка нам гарантирует, что rn\rn—1. Из предпоследней строки следует, что rn\rn—2 и т. д. Из третьей строки следует, что rn\r, из второй, что делит b, а из первой, что rn\a.

Теперь проверим, что rn — наибольший делитель, т. е., что он делится на любой s такой, что s\a и s\b. Теперь просматриваем нашу табличку сверху вниз. Из первой строчки следует, что s\r, из второй, что s\r1 и т. д. Из предпоследней строки следует, что s\rn. Таким образом, последняя строка даже не понадобилась.

б) Осталось выразить остаток rn через исходные элементы a и b. Для этого опять просматриваем нашу табличку снизу вверх. Из предпоследней строки получаем rn =rn—2+(—qn)rn—1, из третьей снизу rn—1=rn—3+(—qn—1)rn—2, поэтому

Поднимаясь снизу вверх, мы последовательно выразим rn через rn—2 и rn—1, потом через rn—3 и rn—2 и т. д. И, наконец, через a и b.

Таким образом, в кольце целых чисел и кольце многочленов над полем всегда можно эффективно найти НОД. Алгоритм, приведенный выше, его называют алгоритмом Евклида, реализован в большинстве компьютерных систем, в том числе и в тех, что используются для нужд криптографии.

Данная теорема имеет массу приложений, например, с ее помощью строятся поля Галуа.

Теорема (Первая теорема о поле Галуа).

Если натуральное число p является простым, то кольцо вычетов Zp на самом деле является полем.

Эта теорема была доказана в п.5 §3 Главы 1 как утверждение.

Упражнение. Найдите обратные по умножению к остатку 5 в полях Z7, Z17, Z127. Проще всего обратный искать по алгоритму Евклида.

1.4. Основная теорема арифметики.

Название это несколько устарело, но сама теорема об однозначном разложении на простые множители не устарела. Теорема эта несколько суховата и аккуратно ее сформулировать не так-то просто. Но на ней, как на фундаменте держится вся арифметика, и все приложения теории чисел. Эта же теорема имеет место и для кольца многочленов над полем, а более широко для всех евклидовых колец. Для них мы ее и докажем.

Однозначность далеко не всегда имеет место. Например, игрушку Лего как не разбирай, простейшие детали окажутся одни и те же. А вот огурец можно разрезать вдоль, а можно и поперек.

Что понимать под однозначностью разложения на простые множители. Например, число 10 можно записать разными способами в виде произведения

.

Определение. Два разложения элемента “a” коммутативного кольца К на простые множители

называются ассоциированными, если — обратимые элементы, n=m, простые элементы pi и qj, возможно после перестановки, попарно ассоциированы, т. е. p1 ассоциирован с q1, p2 ассоциирован с q2 и т. д.

В кольце многочленов простые элементы обычно называют неприводимыми многочленами. Так сложилось исторически, поскольку в прежние времена, разложение многочленов на множители называлось приведением к простому виду. Поэтому, если разложить не удавалось, то и называли неприводимым. Это примерно то же самое, почему у моряков не повар, а кок. Поскольку говорить, что неприводимые элемент кольца многочленов – это простой элемент кольца многочленов, излишний педантизм, то приведем и явное определение.

Определение. Многочлен называется неприводимым, если он не раскладывается в произведение многочленов меньшей степени.

Поиск простых элементов, в том числе и простых чисел и неприводимых многочленов, весьма нетривиальная задача, над которой в мире работают тысячи специалистов и миллионы микропроцессоров. Нам нужно доказать, что в кольце целых чисел Z и кольце P[x] многочленов над полем имеет место однозначное разложение на простые множители. Кстати, на этом факте держится вся криптография с открытым ключом, в том числе и знаменитый RSA.

Как обычно, сделаем это сразу для всех евклидовых колец.

Определение. Говорят, что кольца К является кольцом с однозначным разложением на простые множители, если в нем любой элемент имеет хотя бы одно разложение на простые множители и любые два такие разложения ассоциированы.

Кратко такие кольца называются факториальными. Но можно это слово и не запоминать. Некоторые племена Африки не знают слова зонтик, они просто говорят: “Домик, который белый человек носит в руках и раскрывает над головой, когда идет дождь.”

Фраза в определении факториального кольца о том, что каждый элемент должен иметь хотя бы одно разложение, не ритуальная. Не факт, что такие разложения есть вообще, а про то, чего нет можно доказать все что угодно. Например, я утверждаю, что все алмазы, хранящиеся у меня в доме, имеют вес больше 10 кг. (50 тыс. карат). Что бы меня опровергнуть требуется найти хотя бы один алмаз, который бы весил меньше 10 кг. Такого алмаза найти невозможно потому, что алмазов у меня нет вообще!

В евклидовом кольце любой элемент имеет разложение на простые множители.

Идея доказательства очень проста. Поскольку каждый элемент евклидова кольца имеет степень, а степень сомножителя не больше чем степень произведения, то мы не сможем бесконечно раскладывать на множители. Неразложимые множители и будут простыми элементами. Теперь реализуем эту идею аккуратно. Запустим индукцию по степени элемента “a”. База индукции – неразложимые элементы (независимо от их степени, так что, фактически, имеет место двойная индукция).

Шаг индукции. Пусть , тогда, по предположению индукции сомножители b и c имеют разложение на простые множители, а значит, разложим и исходный элемент “a”.

Самый трудный случай. Пусть , т. е. один из сомножителей не уменьшил свою степень, это допускается определением степени. Тогда применим деление с остатком, «непокорный» элемент “b” поделим на элемент a: .

Следовательно, . Чтобы не возникло противоречия , остается согласиться, что 1–cq=0, т. е. cq=1. Значит элементы a и b ассоциированы, т. е., “а” – и принадлежит базе индукции.

Для кольца с разложением на простые множители есть простой критерий, когда оно является факториальным. Доказательство критерия можно посмотреть, например, в учебнике Введение в алгебру.

Теорема. (Критерий факториальности)

Если кольцо имеет разложение на простые множители, то оно факториально тогда и только тогда, когда для любого простого элемента p из того, что p\(ab) следует, что p\a или p\b.

Критерий кажется очевидным и даже несколько наивным. Однако, если Петю (p) смогли поднять вдвоем Антон (a) и Борис (b) не обязательно, что это они смогут сделать по отдельности.

Теорема (факториальность евклидовых колец).

Любое евклидово кольцо, в частности кольцо целых чисел и кольцо многочленов над полем, являются кольцам с однозначным разложением на простые множители.

Применим критерий факториальности. Пусть простой элемент p делит произведение ab, но не делит элемент a. Так как элемент p простой, то НОД(p,a) = 1 и, значит, в силу алгоритма Эвклида найдутся элементы такие, что ua+vp=1. Умножая это равенство почленно на элемент b, получаем uab+vpb=b. Так как оба слагаемых в левой части равенства делятся на элемент p, то и правая часть делится на p. Значит p\b. Если элемент p не делит b, то аналогично получим, что p\a.

Следствие. В евклидовом кольце число простых элементов бесконечно. В частности, бесконечно число простых чисел и неприводимых многочленов.

Идея использовать метод Евклида для получения новых простых чисел не безнадежна, но мало эффективна. Начнем с первых трех простых чисел 2, 3, 5. Далее получаем , имея четыре числа 2, 3, 5, 31 получим . Вновь появляющиеся числа не только не обязаны быть простыми, но даже и не обязательно дают простые множители, превосходящие предыдущие.

§2. Конечные поля и неприводимые многочлены.

Конечным полем является построенное нам выше кольцо вычетов по простому модулю Zp. В честь великого французского математика Эвариста Галуа (1конечные поля называют полями Галуа и обозначают GF(q), где q – порядок поля.

Нас интересует, что это за число q, можно ли построить два разных (неизоморфных поля), которые имеют одно и тоже число элементов. А главное как поля Галуа задавать на практике и как производить в них вычисления.

Определение. Подмножество L поля P называется подполем, если оно является полем, относительно операций, заданных в поле P. Записывается этот факт стандартно.

Если в поле P выделить как главную операцию, операцию сложения, а умножение на элементы из L рассматривать как действие поля на абелеву группу, то мы увидим, что P – векторное пространство над полем L.

Определение. Размерность векторного пространства P над полем L называется степенью расширения поля P над полем L и обозначается

Теорема (О башне полей).

Если имеется цепочка конечных расширений полей P > L > K, то степень итогового расширения равно произведению степеней промежуточных расширений .

Если базисные элементы векторного пространства P над L умножить поэлементно на базисные элементы пространства L над K, то получится требуемый базис. Это нужно проверить или самому или посмотреть в любой книжке по теории полей.

Теорема (вторая теорема о полях Галуа).

(Таким образом, ответ на один из вопросов получен – число элементов в конечном поле всегда является степенью простого числа. Уже теперь можно утверждать, что полей порядка 6 или 82 не существует.)

а) Пусть Р – конечное поле и e – его нейтральный элемент по умножению. Рассмотрим суммы нейтрального элемента самого с собой: e, e+e, e+e+e, … Т. к. поле конечное, то суммы начнут повторяться, например, ne=me, n P называется полем разложения многочлена f(x), если все корни многочлена f(x) принадлежат полю L, и оно порождается этими корнями. Т. е. это минимальное поле, содержащее все корни многочлена f(x).

Теорема (О поле разложения).

Для любого поля P и любого многочлена существует поле разложения. С точностью до изоморфизма это поле единственно.

идейно совпадает с доказательством с первой теоремы о полях Галуа. Только простой элемент кольца целых чисел заменяется на простой элемент кольца многочленов. Поскольку оба кольца евклидовы, то рассуждения идентичны.

а) Поскольку каждый многочлен однозначно раскладывается в произведение неприводимых многочленов, то можем сразу считать, что многочлен f(x) неприводим.

б) После этого вместо остатков от деления на простое число p рассматриваем все остатки от деления на многочлен f(x). Как и в кольце вычетов вводим операции сложения и умножения. Т. е. в качестве результата берем не обычную сумму и произведение, а остаток от деления на многочлен f(x). Как и в случае колец вычетов проверяется, что получается коммутативное кольцо с единицей.

в) Проверим, что любой ненулевой остаток g(x) имеет обратный по умножению. Т. к. степень многочлена g(x) меньше, чем степень многочлена f(x), а он, в свою очередь, неприводим, то НОД(f(x),g(x))=1. Теперь по алгоритму Евклида в кольце P[x] найдутся многочлены u(x), v(x), такие, что u(x)g(x)+v(x)f(x)=1. Отсюда заключаем, что обратным к остатку g(x) является остаток от многочлена u(x).

г) Теперь можно указать элемент, который в построенном поле остатков, обозначим его L, будет корнем многочлена f(x). Конечно – это остаток, равный многочлену “x”.

д) Теперь в поле L разлагаем многочлен f(x) на неприводимые множители, а хотя бы два множителя появится, ведь один корень уже появился, и возвращаемся к началу доказательства.

е) Вопрос о единственности кажется очевидным – просто добавили корни, а они-то только от многочлена зависят, и получили единственное поле. Однако вопрос гораздо тоньше, но мы его обсуждать не будем.

Поскольку доказательство теоремы несколько описательное и поясняет только идеи (поскольку это не учебник по алгебре), а не детали, то разумно рассмотреть пример.

Пример 1. В современном алгоритме шифрования AES, пришедшем в 26.11.2001 на смену DES, используется конечное поле Галуа GF(28). Это поле является расширением самого маленького поля GF(2), которое состоит из двух нейтральных элементов <0,1>. Неприводимый многочлен, с помощью которого оно строится, согласно стандарта США FIPS-197, имеет вид

Воспользуемся алгоритмом Евклида. Нужно найти такие остатки u, v, что ug+vf=1. Составляем табличку деления с остатком

Теперь нужно выразить последний остаток, равный 1, последовательно через все предыдущие остатки, а потом и через f и g. Обратим внимание, что мы работаем в поле характеристики 2, поэтому x=-x, и (a+b)2=a2+b2:

Потренируйтесь проверяя наш ответ, перемножьте многочлены g и u, а потом найдите остаток от деления на многочлен f. Остаток должен получиться равным 1.

Теорема (Третья теорема о поле Галуа).

Для любого простого числа p и натурального числа n существует единственное поле Галуа GF(pn), которое является полем разложения многочлена .

По теореме о поле разложения, поле разложения нашего многочлена существует и оно единственно. Нужно только проверить, что оно содержит pn элементов. Поскольку наш многочлен имеет степень pn, то получается, что поле разложения должно состоять исключительно из корней самого многочлена!

Вначале проверим, что разных корней ровно pn штук. Т. к. у многочлена над полем не может быть корней больше, чем его степень, то нужно выяснить есть ли кратные корни. Если бы они были, то многочлен и его производная имели бы общие делители. Однако производная многочлена равна (потому, что характеристика поля равна p).

Теперь проверим, что корни образуют в поле разложения подполе, а, значит, совпадают с полем разложения, ведь оно минимальное поле, содержащее все корни.

Пусть a и b – корни нашего многочлена. Нужно проверить, что тогда a+b, ab, —a, a-1, а также 0 и 1, тоже являются корнями многочлена. Для 0 и 1 это очевидно. Далее, по предположению имеем поэтому, не забывая, что характеристика равна p, получаем

Вычисления, выполненные нами при нахождении обратного элемента по умножению, оказались довольно громоздкими. Конечно, на компьютере они будут выполнены мгновенно. Однако, если степень многочлена будет в несколько сотен единиц, и решать придется много уравнений, компьютеру тоже мало не покажется. Кроме того, в машинном виде идеально любые объекты представлять в виде чисел и все сводить к операциям над числами. Но чтобы связать числа с элементами конечного поля нам нужно ввести одно важное понятие.

Определение. Порождающий элемент мультипликативной группы поля, если он существует, называется примитивным элементом.

Теорема (О примитивном элементе).

Любое конечное поле имеет примитивный элемент.

Мы изложим только идею доказательства. Примитивный элемент, если он существует, должен иметь порядок k=pn–1. т. к. именно столько ненулевых элементов в поле GF(pn). Если же примитивного элемента нет, то все ненулевые элементы поля имеют порядки меньшие числа k. Точнее, их порядки должны делить это число, по теореме Лагранжа. И если S=НОК(порядков ненулевых элементов поля) и S n0 для некоторого n0, поэтому широко используются такие конструкции как O(g(n)), o(g(n)).

Вычисляя пределы соотношений при n→∞, 0 n0 для некоторого n0) выполняются соотношения:

Алгоритм, время работы которого составляет eo(n), обладает субэкспоненциальной сложностью.

Те алгоритмы, время работы которых не может быть ограничено таким образом, обладают экспоненциальной сложностью.

Полиномиальные по времени алгоритмы считаются эффективными, а задачи, решаемые такими алгоритмами, объединены в класс P.

Время работы субэкспоненциальных алгоритмов асимптотически выше, чем полиномиальных, но ниже, чем экспоненциальных.

Важным примером субэкспоненциальной функции является

где c > 0, 0 1. Требуется найти его разложение на простые сомножители , где pi – простые числа (i = ), то есть факторизовать n.

Как было показано в Главе 1, с проблемой факторизации тесно связаны такие теоретико-числовые проблемы, как поиск квадратных корней по составному модулю (в том числе и проблема RSA), проблема распознавания квадратов и псевдоквадратов по модулю Блюма, проблема вычисления функции Эйлера. Было показано, что каждая из этих проблем не сложнее проблемы факторизации, а некоторые из проблем ей эквивалентны. Во всяком случае, решив задачу факторизации, дальнейшее решение каждой из этих проблем осуществляется за полиномиальное время.

Поэтому задача факторизации представляется столь важной, и количество разнообразных алгоритмов факторизации весьма велико. Конечно же, невозможно привести всевозможные алгоритмы в рамках одного параграфа ввиду не только их количества, но и сложности. Далее приведены некоторые алгоритмы факторизации, которые иллюстрируют основные направления в исследовании данного вопроса.

Прежде чем приступить к факторизации числа, необходимо учесть следующее:

1) Если n – четное число, то следует выделить из него все степени двойки. Такая операция является легкой, особенно если число n представлено в двоичной форме. Тогда выделение степеней двойки – это битовый сдвиг вправо до тех пор, пока в младшем бите не появится «1».

2) Проверка на простоту проще, чем факторизация, поэтому прежде чем начать факторизацию нечетного n, следует проверить его на простоту.

3) Следует проверить, не является ли n целочисленной степенью какого-либо числа (n = xk). Такая задача решается вычислением для всех целых k [2,log2n] (если n предварительно проверено на четность, то k [2,log3 n]).

4) Следует рассмотреть задачу 2-факторизации (сплиттинга), или расщепления n=a∙b (1 B. (чередуем шаг +2 и +4 с тем, чтобы отсеять числа, кратные «2» и «3»).

Ш.2. Осуществляем пробное деление на di. Если di\n, то n=n/di и повторяем

Шаг 2. Если di не делит n, то идем на Шаг 3.

Ш.3. Уничтожаем di, освобождаем память.

Заметим, что все малые делители, выделенные вышеуказанным способом, будут простыми.

2.2. Метод Ферма.

Метод специального назначения, применяется для 2-факторизации, или сплиттинга.

Ш.1. Вычисляем x=+1.

Ш.2. Если x=, то идем на Выход с сообщением «n – простое число».

Ш.3. Вычисляем z=x2—n и y=. Если y2=z, то идем на Выход, a=x+y, b=x—y.

Отметим, что делители a и b, получившиеся в результате 2-факторизации Ферма, в общем случае не являются простыми и требуют проверки на простоту и дальнейшей факторизации.

2.3. Метод квадратичного решета.

Пусть n – число, которое надо факторизовать. Как и метод Ферма, данный метод ищет целые числа x, y: n=x2—y2, но подход к поиску несколько иной. Поиск числа x осуществляется не среди всех чисел подходящего размера. Перед началом перебора производится отсев некоторых чисел.

Источник