если первое число месяца попадает на понедельник то какое число будет на третий понедельник

14.07.202217.07.2022 admin 0 Comments

Если первое число месяца попадает на понедельник то какое число будет на третий понедельник

a) Почти все годы XIX века записываются так: 18.. (исключение — 1900 год, который нам, очевидно, не подходит). Поэтому, чтобы год читался одинаково справа налево и слева направо, оставшиеся две цифры должны быть 81.

Заметим, что в каждом году может быть не более одной даты-палиндрома. Действиетельно, если уже написан номер года (например, 2012), то число и месяц даты-палиндрома в этом году звписываются теми же цифрами в обратном порядке (в нашем примере 21.02). То есть по номеру года дата-палиндром (если она есть) определяется однозначно.

Таким образом, в 2012 году нет дат-палиндромов, кроме указанной. Попробуем найти предыдущую дату-палиндром в 2011 году. Это будет 11.02.2011.

Следующая дата-палиндром будет не раньше 2013 года. Попробуем найти такую дату в 2013 году. Но это может быть только 31.02.2013, а такой даты нет, поскольку в феврале 2013 года всего 28 дней. Значит, в 2013 году дат-палиндромов не будет. По аналогичным причинам дат-палиндромов не будет и с 2014 по 2019 год. А вот в 2020 году дата-палиндром найдётся: это будет 02.02.2020.

a) Пять понедельников всегда будет в месяце, начинающемся с понедельника (если только это не февраль невисокосного года). Шести понедельников в одном месяце быть не может. Действительно, тогда в таком месяце было бы как минимум пять полных недель и ещё один понедельник, то есть не менее 7·5+1=36 дней, а такого не бывает.

b) 365 = 52·7 + 1, 366 = 52·7 + 2. Поэтому в каждом году не более 52 полных недель (от понедельника до воскресенья). Если год начинается с понедельника, то каждая из 52 полных недель будет начинаться с понедельника, а 31 декабря тоже будет понедельником. Поэтому в этом случае в году будет 53 понедельника. А если бы в каком-то году было хотя бы 54 понедельника, то в нём было бы не меньше 53 полных недель, чего быть не может.

Часть II

Часть III

Выпишем номера дней года, на которые попадают 13-е числа разных месяцев. 13 января, очевидно, будет тринадцатым днём года. 13 февраля будет 31+13=44-м днём года, 13 марта будет 31+28+13=72-м днём года (будем пока считать, что наш год невисокосный). Далее аналогично находим: 13 апреля — 103-й день, 13 мая — 133-й день, 13 июня — 164-й день, 13 — июля 194-й день, 13 августа — 225-й день, 13 сентября — 256-й день, 13 октября — 286-й день, 13 ноября — 317-й день, 13 декабря — 347-й день. (Номера тринадцатых чисел в високосном году посчитайте самостоятельно.)

Посмотрим на остатки от деления этих номеров на 7. Получим: 6, 3, 2, 5, 0, 3, 5, 1, 4, 6, 2, 4 (проверьте!). Для високосного года эти остатки будут равны, соответственно, 6, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5. Заметим, что в обоих списках встречаются все возможные остатки от деления на 7 (от 0 до 6).

Номера всех дней года, приходящихся на пятницу, имеют один и тот же остаток от деления на 7 (так как пятница бывает раз в 7 дней). Кроме того, все дни года, номера которых дают одинаковый остаток при делении на 7, приходятся на один и тот же день недели (потому что в неделе 7 дней). Как мы выяснили, номера дней года, приходящихся на 13-е числа разных месяцев, дают все возможные остатки от деления на 7. Поэтому, какой бы остаток от деления на 7 ни давали номера пятниц, всегда найдётся 13-е число какого-нибудь месяца, номер которого делится на 7 с тем же остатком. Это и будет «пятница 13-е».

Источник

МАТЕМАТИЧЕСКИЕ ОЛИМПИАДНЫЕ ЗАДАЧИ

1. Может ли быть в одном месяце быть 5 понедельников и 5 четвергов? Обоснуйте ответ.

Если в месяце 31 день, и он начинается с понедельника, то в нём может быть 5 понедельников, 5 вторников и 5 сред, но остальных дней недели по четыре, так как 5+5+5+4+4+4+4=31. Ответ: не может.

2. Может ли в феврале высокосного года быть 5 понедельников и 5 вторников? Ответ обоснуйте.

Только в феврале высокосного года может быть 5 понедельников и по 4 остальных дней недели, т.е. в сумме – 29 дней. Ответ: не может.

3. В феврале 2004 года 5 воскресений, а всего – 29 дней. На какой день недели приходится 23 февраля 2004 года?

Если в феврале 29 дней и 5 воскресений, то первое воскресение будет 1 февраля. Отсюда 23 февраля – понедельник.

4. В некотором месяце три пятницы пришлись на чётные числа. Какой день недели был 15 числа этого месяца?

Три пятницы, выпадающие на чётные числа месяца, могут быть только 2, 16 и 30 числа. 15 числа был четверг.

5. Известно. Что 1 декабря приходится на среду. На какой день недели приходится 1 января следующего года?

Среда 1, 8, 15, 22, и 29 декабря, четверг 30, пятница 31. Ответ: суббота 1 января следующего года.

6. В некотором месяце три воскресенья пришлись на чётные числа. Какой день недели был 20 числа этого месяца?

Четные воскресенья 2, 16, 28. Значит 20 число этого месяца – четверг.

7. Какое наибольшее число воскресений может быть в году?

8. Какое самое большое число месяцев с пятью воскресениями может быть в году?

5 месяцев. Обычный год при этом должен начинаться с воскресенья, а високосный – с субботы или воскресенья.

9. В каком-то году некоторое число ни в одном месяце не было воскресеньем. Какое это могло быть число?

31-е число и только одно. Например, в 2007 году ни одно воскресенье не было 31 числом.

10. В некотором месяце три субботы пришлись на четные числа. Какой день недели был 28-го числа этого месяца?

Пусть первая «четная» суббота пришлась на число, которое обозначим через х ( х – четное число). Следующая четная суббота будет через две недели, т.е. (х+14) –го числа, а третья «четная» суббота – (х+28) –го числа. Но в месяце не более 31 дня, следовательно, х+28≤ 31. У этого неравенства одно еётное решение х=2. Тогда третья «четная» суббота была 30-го числа, а 28-го был четверг.

11. В некотором месяце три пятницы пришлись на четные числа. Какой день недели был 15 числа этого месяца?

12. В некотором месяце три воскресенья пришлись на четные числа. Какой день недели был 20 числа этого месяца?

13. Докажите, что первый и последний день 2010 года – это один и тот же день недели.

2010 год не високосный 2. Обычный год содержит 365=52х7+1 дней, т.е. 52 полных недели плюс один день. Поэтому любой обычный год начинается и заканчивается на один и тот же день недели. Для 2010 года это будет пятница.

14. В некотором месяце понедельников больше, чем вторников, а воскресений больше, чем суббот. Какой день недели был 5-го числа этого месяца? Мог ли этот месяц быть декабрем?

За 4 недели, с 1 по 28-е число, каждый день недели встречается ровно 4 раза, поэтому из условия следует, что 29-е – воскресенье, 30-е – понедельник, а 31-го числа в этом месяце нет. Следовательно, месяц, о котором идет речь, начался с воскресенья, а его 5-е число было четвергом. Данный месяц декабрём быть не мог: в декабре 31 день.

15. В некотором году три месяца подряд содержали всего по четыре воскресенья. Докажите, что один из этих месяцев – февраль.

Если февраль не входит в указанные «три месяца подряд», то сумма дней – 91 или 92. Но 91=7х13, 92=7х13+1, т. е в этом случае три месяца содержат 13 полных недель, значит, и каждый день недели, в том числе воскресенье, содержится 13 раз, и условие не выполняется. Тем самым доказано, что один из трех месяцев должен быть февралём, причем в обычном году достаточно, чтобы из трёх месяцев был февралём, а в високосном – эти три месяца: февраль(29), март(31), апрель(30). К тому же необходимо, чтобы последний день третьего месяца был субботой.

16. У большинства Петиных одноклассников день рождения в 1995 году пришёлся на четверг. В 1996 году у большинства одноклассников он пришёлся на пятницу. А на какой день недели он приходился в 1997 году?

1995 и 1997 годы не високосные (по 365 дней), а 1996 – високосный (366 дней). При переходе от 1995 года к 1996 году любое число сместится на один день недели вперёд. Но при переходе от 1996-го високосного, смещение будет на два дня вперёд, т. е. день рождения, приходившийся на пятницу, сместится на воскресенье.

17. Год 2000 обозначается всего двумя римскими цифрами ММ. Какой год из прошедших 2000 лет содержит максимальное количество римских цифр в своей записи?

18. Один человек обнаружил в 1937 году, что в 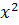-м году ему было х лет, и сказал: «Если к числу моих лет прибавить порядковый номер месяца моего рождения, то получится квадрат дня моего рождения. Когда родился этот человек?

Источник

Математические закономерности в календаре

Ищем педагогов в команду «Инфоурок»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №16

Научно-практическая конференция «Старт в науку»

«Математические закономерности в календаре»

АКТУАЛЬНОСТЬ ……………………………………………..…………..………. 3

МАТЕМАТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ В КАЛЕНДАРЕ

Исследование «Четырехугольники в календаре»

Исследование «Треугольники в календаре

Исследование «Пятница 13-е»

Занимательные закономерности в календаре

Математические фокусы и календаре

Интересные факты о календаре

Математические олимпиадные задачи

В наше время нет человека, который не знал бы, что такое календарь. К его услугам мы прибегаем ежедневно. Мы настолько привыкли пользоваться календарем, что даже не можем себе представить современное общество без упорядоченного счета времени

Меня с детства интересовали эти цветные карточки с нанесенными на них такими

знакомыми и таинственными датами. Особый интерес к настенному календарю у меня появился после задачи, которую нам предложил учитель на уроке геометрии, при изучении темы «Прямоугольные треугольники»: «Если соединить числа 10,20, и 30 января 2006 года, то получится равнобедренный прямоугольный треугольник. Докажите это. Задача про календарь и треугольники оказалась нестандартной задачей на признаки равенства треугольников и вызвала у большинства учащихся интерес и много вопросов. По совету учителя я продолжил исследование задачи и постарался ответить на возникшие вопросы. Результатом моего исследования стала работа «Математические закономерности в календаре».

Вопросы, на которые мне бы хотелось получить ответ:

Получится ли равнобедренный прямоугольный треугольник, если соединить числа 10,20, и 30 января в любом году?

Каков будет результат, если будем соединять числа 10, 20 и 30 любого месяца одного года?

Получится ли равнобедренный прямоугольный треугольник, если соединим другие числа в любом месяце?

Определение предмета исследования

Исследовав задачу про календарь и треугольники, я задался вопросом: есть ли ещё в математической литературе задачи по теме «Календари»? Из Интернет-ресурсов узнал об истории календаря, видах календарей, но нам нужны были только задачи по данной теме Оказалось, что такие задачи встречаются часто на олимпиадах различных уровней.

Решение задач, связанных с календарем, столкнуло меня с проблемой: мало знаний по данному вопросу. Чтобы решать подобные задачи, надо знать некоторые особенности календаря. Поэтому, предметом исследования стали табель–календари различных лет.

1. Можно ли использовать настенный календарь на уроках математики? Для этого надо выяснить есть ли ещё в математической литературе задачи по теме «календари», которые можно предлагать на уроках, олимпиадах и различных математических турнирах.

2. Какими особенностями обладают табель–календари?

3 Выдвижение гипотезы

Гипотеза исследования связана с предположением, что, изучив особенности табель–календарей, можно исследовать немало задач по теме «Календари», которые украсят уроки математики, и их можно применять и во внеклассной работе: олимпиадах, турнирах, конкурсах, марафонах и т.д.

Для достижения желаемого результата были использованы различные методы:

Данный раздел состоит из двух частей. В первой части – исследование задач: про календарь и треугольники и квадраты в календаре. Во второй части выявили особенности календарей, знания которых позволяют решать подобранные нами задачи по теме «Календари».

Почему в неделе 7 дней?

Вы никогда не задумывались, почему в неделе семь дней? Не пять, не девять, а именно семь? По-видимому, обычай измерять время семидневной неделей пришёл к нам из Древнего Вавилона и связан с изменениями фаз Луны. Люди видели Луну на небе около 28 суток: семь дней – увеличение до первой четверти, примерно столько же – до полнолуния и т.д.

Счёт был начат с субботы, первым её часом «управлял» Сатурн (следующие часы – в обратном порядке планет). В итоге первым часом воскресенья управляло Солнце, первым часом третьего дня (понедельника) – Луна, четвёртого – Марс, пятого – Меркурий, шестого – Юпитер, седьмого (пятницы) – Венера. Соответственно, такие названия и получили дни недели.

Решение о праздновании воскресенья принял ещё римский император Константин в 321 г.

Возможно, неделя, состоящая из семи дней – это оптимальное сочетание труда и отдыха, напряжения и праздности. Как бы то ни было, жить нам всё равно приходится по тому или иному, но распорядку.

Почему дата Пасхи меняется каждый год.

Если вы заметили, праздник Пасхи не закреплён за каким-то определённым числом, как все остальные праздники. Каждый год Пасха выпадает на разные числа, а иной раз — и на разные месяцы. Есть разные способы нахождения даты Пасхи.

Немецкий математик Гаусс в XVIII веке предложил формулу для определения дня Пасхи по григорианскому календарю математическим способом.

2016 :19 = 106 (ост. 2 – а ) 2016 :19 = 106 (ост. 2 – а )

2016 : 4 = 504 (ост. 0 – б )

2016 : 7 = 288 (ост. 0 – в )

( 19 ∙ 2 + 15) : 30 = 1 (ост. 23 – г )

(2б +4в + 6г + 6) : 7 = 20 (ост. 4 – д )

23 + 4 > 9 пасха в апреле

Прибавляя 13 дней получаем 1 мая2016г.

математические закономерности в календаре

«ЧЕТЫРЕХУГОЛЬНИКИ В КАЛЕНДАРЕ»

Таинственные квадраты в календарях.

Заметим, что в любом месяце можно выделить квадраты, состоящие из четырех чисел (2х2), из девяти чисел (3х3) и из шестнадцати чисел (4х4).

Какими свойствами обладают такие квадраты?

Складывая числа, получим 9 m +72=9( m +8). Значит, сумму чисел таких квадратов можно находить, если к меньшему числу прибавить 8 и сумму умножить на 9.

Значит, сумму чисел обведенного квадрата 3×3 можно найти, если из большего числа вычесть 8 и разность умножить на 9.

Получим, 16Р-192=16(Р-12). Значит, сумму чисел в любом квадрате из 16-ти чисел можно находить по правилу: Из большего числа вычитаем 12 и умножаем на 16.

(30-12)∙16=288 или к меньшему числу прибавить 12 и умножить на 16. (6+12) ∙16=288

Чтобы найти сумму 16-ти чисел достаточно умножить сумму двух чисел, стоящих на противоположенных концах любой диагонали, обведенного квадрата на 8.

Выведенные свойства квадратов в настенных календарях можно применять на уроках математики при изучении темы «Сложение натуральных чисел», на устном счете и во внеклассной работе, показывая фокусы.

«ТРЕУГОЛЬНИКИ В КАЛЕНДАРЕ»

Если соединить числа 10, 20, 30 в январе 2016г, то получим равнобедренный прямоугольный треугольник.

Следовательно, сумма углов, дополняющих угол 30 до развернутого угла, равна сумме острых углов треугольника 31 – 10 – 30. Значит, угол 10 тоже равен 90˚. Итак, треугольник 10 – 20 – 30 является равнобедренным прямоугольным.

Числа 10, 20, 30 отстоят друг от друга на 10 единиц. При их соединении получим равнобедренный прямоугольный треугольник. Аналогично, прямоугольный треугольник получится если соединить другие числа, отстоящие друг от друга на 10 единиц. Например, соединим числа 1, 11, 21; 2, 12, 22; 3, 13, 23; 4, 14, 24; 5, 15, 25; 6, 16, 26; 7, 17, 27; 8, 18, 28; 9, 19, 29; 11, 21, 31.

Если в календаре любого года соединить числа 10, 20 и 30 января, то получится равнобедренный прямоугольный треугольник.

Расположение чисел 10, 20 и 30 в январе будет зависеть от того, каким днем недели будет 1 января.

Вывод. Календари обладают следующей особенностью: если в календаре любого года соединить числа соответствующие 10, 20 и 30 января, то получится равнобедренный прямоугольный треугольник, за исключением случаев, где центры клеток с числами 10, 20 и 30 лежат на одной прямой.

ИССЛЕДОВАНИЕ «ПЯТНИЦЫ 13

Пятница 13-го числа любого месяца – распространенная примета, по которой в такой день следует быть особенно готовым к неприятностям и остерегаться неудач.

Цель исследования: выяснить, какое максимальное (минимальное) число пятниц в одном году может попадать на число 13.

День недели, выпавший на 1 января

2007, не високосный

2013, не високосный

2014, не високосный

2015, не високосный

Февраль, март, ноябрь

2010, не високосный

2011, не високосный

2006, не високосный

Январь, апрель, июль

Какой бы ни был год (високосный или не високосный) не может быть года, в котором 13 – е число хотя бы один раз не пришлось на пятницу.

Минимальное число пятниц, приходящихся на 13 число – одна. В не високосный год пятница 13-е может быть только: в мае, или в июне, или в августе. В високосном году пятница 13-е может быть только: в мае, или июне, или октябре.

Максимальное число пятниц приходящихся на 13 число три. В не високосный год (год начинается с четверга) пятница 13-е выпадает: на февраль, март и ноябрь. В високосном году (год начинается с воскресенья) пятница 13-е выпадает на: январь, апрель и июль.

ЗАНИМАТЕЛЬНЫЕ ЗАКОНОМЕРНОСТИ В КАЛЕНДАРЕ

Любой не високосный год начинается и заканчивается одним и тем же днем недели (2013 год начался со вторника и вторником закончился). Високосный год заканчивается со сдвигом на 1 день недели (2012 год начался с воскресенья, а закончился понедельником).

В високосный год на один и тот же день недели в году приходятся:

а) 1 января и 1 октября;

б) 1 февраля, 1 марта и 1 ноября;

г) 1 сентября и 1 декабря.

Если в некотором году 1 января – понедельник, а 1 октября – вторник, то год будет високосный.

Все месяцы как високосного, так и не високосного года, можно разделить на 7 групп по признаку, на какой день недели приходится 1 число месяца.

1 группа: январь и октябрь;

2 группа: февраль, март и ноябрь;

3 группа: апрель и июль;

7 группа: декабрь и сентябрь.

В году будет больше тех дней недели, с которых они начинаются. Так, 2009 год – не високосный, начался и закончился четвергом, значит, четвергов в году будет 53, а остальных дней недели 52.

Четные (нечетные) недели месяца повторяются через 2 недели, если первая четная среда 2 числа, то следующие четные приходятся на 16, 28.

Чтобы это сделать, вам нужно прибавить к названному числу 8 и результат умножить на 9.

Вечные календари в основном представляют собой таблицы.

Календарь с 1901 по 2096 год

Алгоритм: для того, чтобы узнать день недели конкретного дня, требуется:

Сложить эту цифру с номером дня;

Найти во второй таблице получившееся число и посмотреть, какому дню недели оно соответствует.

Числу 25 в таблице 2 соответствует четверг — это и есть искомый день недели.

РАЗДЕЛ II. ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ

3.1. МАТЕМАТИЧЕСКИЕ ФОКУСЫ И КАЛЕНДАРЬ

На принципе закономерностей, полученных в ходе исследования календаря, строятся несколько фокусов «быстрых вычислений».

1. Фокус-предсказание. В этом фокусе фокусник может показать свой дар прорицания и умеет производить в уме быстрое сложение нескольких чисел. Попросите зрителя обвести на настольном календаре в любом месяце любой квадрат из 16 чисел. Бегло взглянув на него, вы записываете на листке предсказание, кладете его в конверт и отдаете на хранение зрителю. Затем просите зрителя выбрать любое число в этом календаре, обвести его кружком и вычеркнуть все числа, находящиеся в той же строчке и том же столбце, что и только что обведенное число. В качестве второго числа зритель может обвести кружком любое число, оставшееся незачеркнутым. После этого он должен вычеркнуть третье число, а соответствующие строчка и столбец вычеркиваются.

В финале вы эффективно предлагаете достать из конверта листок и убедиться, что на нем заранее вами была написана именно эта сумма чисел.

Чтобы это сделать, вам нужно было сложить два числа, находящихся на двух диагонально противоположных углах квадрата и найденную сумму удвоить.

2. Фокус с нахождением суммы. В этом фокусе фокусник очень быстро может отгадать сумму чисел, входящих в обведенный квадрат на календаре. Для этого попросите зрителя обвести на настенном календаре в любом месяце квадрат, содержащий 16 чисел. Бегло взглянув на него и производя в уме необходимые вычисления, называете сумму всех чисел, попавших в этот квадрат.

Чтобы это сделать, вам нужно было умножить сумму двух чисел, стоящих на противоположных концах любой диагонали, обведенного квадрата, на 8.

ИНТЕРЕСНЫЕ ФАКТЫ О КАЛЕНДАРЕ

1. На сегодняшний день невозможно точно сказать, сколько всего существовало календарей. Вот максимально полный их список: Армелина, Армянский, Ассирийский, Ацтекский, Бахаи, Бенгальский, Буддийский, Вавилонский, Византийский, Вьетнамский, Гильбурда, Голоценский, Григорианский, Грузинский, Древнегреческий, Древнеегипетский, Древнеиндийский, Древнекитайский, Древнеперсидский, Древнеславянский, Еврейский, Зороастрийский, Индийский, Инки, Иранский, Ирландский, Исламский, Китайский, Конта, Коптский, Малайский, Майя, Непальский, Новоюлианский, Римский, Симметричный, Советский, Тамильский, Тайский, Тибетский, Туркменский, Французский, Ханаанейский, Чучхе, Шумерский, Эфиопский, Юлианский, Яванский, Японский. [4]

2. Коллекционирование карманных календарей называется филотаймией или календаристикой. [7]

3. За все время существования календаря время от времени появлялись очень оригинальные и необычные календари. Например, календарь в стихах. Первый из них был выпущен на одном листе, в виде настенного плаката. Календарь «Хронология» был составлен Андреем Рымшей и отпечатан в городе Остроге Иваном Федоровым 5 мая 1581 года. [4]

4. Самый первый календарь в виде миниатюрной книги вышел из печати в канун 1761 года. Это «Придворный календарь», который до сих пор можно увидеть в Государственной публичной библиотеке имени М. Е. Салтыкова-Щедрина в Санкт-Петербурге. [4]

5. Первые русские отрывные календари появились в конце XIX века. Их начал печатать издатель И. Д. Сытин по совету, который дал ему никто иной, как… Лев Николаевич Толстой. [4]

6. Первый карманный календарь (размером примерно с игральную карту), с иллюстрацией на одной стороне и самим календарем – на другой впервые был выпущен в России в 1885 году. Он был отпечатан в типографии «Товарищества И. Н. Кушнаерева и К°». Эта типография существует до сих пор, только называется она теперь «Красный пролетарий». [4]

7. Самый маленький календарь в истории весит всего 19 грамм вместе с переплётом. Он хранится в Матенадаране (Армянский институт древних рукописей) и представляет собой рукопись размером менее спичечного коробка. Он содержит 104 пергаментных листка. Он написан каллиграфическим почерком писца Огсента и доступен для чтения только с помощью увеличительного стекла. [4]

не только книг, но и календарей. Здесь собрано около 40 тысяч наименований календарей всех разновидностей. [4]

МАТЕМАТИЧЕСКИЕ ОЛИМПИАДНЫЕ ЗАДАЧИ

1. Может ли быть в одном месяце быть 5 понедельников и 5 четвергов? Обоснуйте ответ.

2. Может ли в феврале високосного года быть 5 понедельников и 5 вторников? Ответ обоснуйте.

Только в феврале високосного года может быть 5 понедельников и по 4 остальных дней недели, т.е. в сумме – 29 дней. Ответ: не может.