хватит ли для кодирования трех букв кодовых слов длиной 2 бита
Содержание урока
Равномерные коды
Равномерные коды
Если нам нужно записать в память компьютера какой-то текст на русском языке, его нужно представить в виде двоичного кода, т. е. перекодировать.
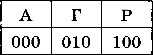
Например, перекодируем слово ГАГАРА в двоичный алфавит, считая, что в тексте есть только буквы «А», «Г» и «Р», т. е. алфавит состоит из трёх знаков. Присвоим каждой из этих букв двоичные коды — кодовые слова (рис. 2.5).
Закодируйте с помощью этого кода слово ГАГАРА.
Такой код называется равномерным, потому что длина всех кодовых слов одинакова.

Теперь предположим, что по компьютерной сети передана цепочка
000010000100000010000100
Известно, что для кодирования использовалась таблица, показанная на рис. 2.5, и нам нужно узнать, какое сообщение было закодировано. Эта операция называется декодированием.

Сообщение 000010000100000010000100 закодировано с помощью равномерного кода, приведённого на рис. 2.5. Определите, сколько знаков было в исходном сообщении. Как вы рассуждали? Декодируйте это сообщение.
Равномерный 5-битный двоичный код, разработанный в конце XIX века Жаном Морисом Бодо, использовался в телеграфных аппаратах. В современных компьютерных системах при передаче текстовых сообщений также часто применяют равномерный (8-битный или 16-битный) код.
Можно ли было для кодирования букв «А», «Г», «Р» использовать более короткий равномерный код? Определите наименьшую возможную длину кодовых слов.
Если для кодирования используется алфавит мощностью M, то с помощью кодовых слов длиной L можно закодировать M L различных знаков. Это число должно быть не меньше, чем мощность алфавита исходного сообщения M0, потому что иначе какие-то буквы обязательно получат одинаковые коды.
Длину кодовых слов L выбирают из условия M L ≥ M0, где М0 — мощность алфавита исходного сообщения и М — мощность нового алфавита.
Как выбрать наименьшую возможную длину кодовых слов при равномерном кодировании?
В сообщении используются 33 русские прописные буквы и пробел. Определите наименьшую длину кодовых слов для равномерного кодирования этого сообщения в трёхбуквенном и четырёхбуквенном алфавитах.
Следующая страница 
Cкачать материалы урока
Хватит ли для кодирования трех букв кодовых слов длиной 2 бита
Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Л использовали кодовое слово 1, для буквы М – кодовое слово 01. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Условие Фано — никакое кодовое слово не может быть началом другого кодового слова. Так как уже имеется кодовое слово 1, то никакое другое не может начинаться с 1. Только с 0. Также не может начинаться с 01, поскольку у нас уже есть 01. То есть любое новое кодовое слово будет начинаться с 00. Но это не может быть 00, так как иначе мы не сможем взять больше ни одного кодового слова, поскольку все более длинные слова начинаются либо с 1, либо с 00, либо с 01. Мы можем взять либо 000, либо 001. Но не оба сразу, поскольку опять же в таком случае мы больше не сможем взять ни одного нового кода. Тогда возьмём 001. И так как нам осталось всего два кода, то можем взять 0000 и 0001. Итого имеем: 1, 01, 001, 0000, 0001. Всего 14 символов.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В и Г, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Для букв А, Б, В используются такие кодовые слова: А — 000, Б — 1, В — 011.
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Код не может начинаться с 1, так как Б − 1.
0 не подойдёт, так как А и В начинаются с 0.
Двоичные коды 00 или 01 не подходят, поскольку А и В — 000 и 011.
010 и 001 подойдут, так как не конфликтуют ни с каким другим уже имеющимся кодом, из них 001 меньше.
Хватит ли для кодирования трех букв кодовых слов длиной 2 бита
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: В — 1110, Г — 110, Д — 0000, Е — 01. Известно, что для кодирования слова БАОБАБ потребовалось 16 двоичных знаков. Какое кодовое слово соответствует букве А?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Кодовыми словами для буквы А не могут быть 0 или 1, поскольку будет нарушаться условие Фано. Поскольку буква Б встречается в слове БАОБАБ 3 раза, возьмём кодовое слово для буквы Б равным 10. Буква А встречается в слове БАОБАБ 2 раза, значит, кодовым словом для буквы А будет 001. Букву О закодируем кодовым словом 0001. Тогда для кодирования слова БАОБАБ потребуется 16 двоичных знаков. Значит, ответ — 001.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 10, Г — 1110, Д — 0111, Е — 010. Известно, что для кодирования слова АНАНАС потребовалось 16 двоичных знаков. Какое кодовое слово соответствует букве Н?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Кодовыми словами для буквы Н не могут быть 0 или 1, поскольку будет нарушаться условие Фано. Поскольку буква А встречается в слове АНАНАС 3 раза, возьмём кодовое слово для буквы А равным 00. Буква Н встречается в слове АНАНАС 2 раза, значит, кодовым словом для буквы Н будет 110. Букву С закодируем кодовым словом 0110. Тогда для кодирования слова АНАНАС потребуется 16 двоичных знаков. Значит, ответ — 110.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Для двух букв кодовые слова уже известны, осталось подобрать для оставшихся двух букв такие кодовые слова, которые будут являться кратчайшими и удовлетворять условию Фано.
Кодовые слова не могут начинаться с 0, поскольку 0 является кодовым словом для буквы А. Кодовым словом для буквы В будет являться 1100, кодовые слова 11, 110 и 111 использовать нельзя, поскольку не получится закодировать остальные буквы таким образом, чтобы возможная сумма длин кодовых слов для букв В, Г, Д и Е была наименьшей. Кодовым словом для буквы Г будет являться 1101, для буквы Д — 1110, а для буквы Е — 1111.
Таким образом, сумма кратчайших кодовых слов для букв В, Г, Д и е будет равняться 4 + 4 + 4 + 4 = 16.
5. Кодирование и декодирование
Для кодирования последовательности, состоящей из букв слова ШKOЛKOВО решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Ш использовали кодовое слово 00, для буквы К — 1. Укажите, какова наименьшая длина всех символов заданного слова.
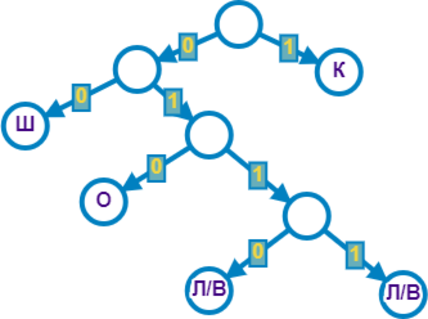
Построим дерево для решения задачи. Для букв Ш и К есть кодовые слова 00 и 1 соответственно. В слове ШКОЛКОВО самая частовстречаемая буква — О, следовательно, её нужно закодировать минимальновозможным количеством символов.
Минимально возможная длина кодового слова для буквы состоит из трёх битов, то есть О закодируем с помощью 010.
Буквы Л и В встречаются всего один раз, закодируем их минимально возможным количеством символов.
Самая маленькая длина кодовых слов для них \(=4\) : 0110 и 0111.
Посчитаем сумму длин кодовых слов:
Ш, Л и В встречаются один раз,
Для кодирования последовательности, состоящей из букв слова Р, Б, О, Т, А используется неравномерный двоичный код, удовлетворяющий прямому условию Фано.
Вот этот код: А – 0; Р – 100; Б – 1010; О – 111; Т – 110. Необходимо сократить для одной из букв длину кодового слова так, чтобы код можно было однозначно декодировать.
Для какой буквы это возможно сделать? В ответе укажите эту букву.
Так как код удовлетворяет прямому условию Фано (ни одно кодовое слово не является началом другого), то следует учитывать это при сокращении исходных кодовых слов.
1. Код буквы А сократить нельзя, так как он состоит всего из одного символа.
2. Р сократить нельзя,так как при сокращении до 10 код перестанет удовлетворять прямому условию Фано.
3. Б возможно сократить до 101, в таком случае код по-прежнему будет удовлетворять одному из условий Фано (прямому).
4. О нельзя сократить, т.к. в этом случае нарушится прямое условие Фано.
5. Код буквы Т нельзя сократить, т.к тогда он совпадёт с началом кода буквы О, что недопустимо при выполнении прямого условия Фано.
По каналу связи передаются сообщения, которые содержат только следующие буквы: С, Т, Р, И, М; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв С, Т, Р используются такие кодовые слова: С – 0; Т – 110; Р – 101. Укажите кратчайшее кодовое слово для буквы И, при котором код будет допускать однозначную расшифровку. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Построим дерево решений. Код не может начинаться с нуля, т.к из данной вершины нельзя построить новые варианты, удовлетворяющие условию Фано. Из схемы видно, что для букв И, М есть два возможных варианта кодировки,которые начинаются с 1.
Первый вариант: 111
Второй вариант: 100
Оба варианта удовлетворяют условию Фано (не являются началом других кодовых слов), нам подходит вариант с наименьшим значением, то есть 100 — ответ.
Хватит ли для кодирования трех букв кодовых слов длиной 2 бита
Тема: Кодирование и декодирование информации.
· кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите)
· обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход
· один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия)
· кодирование может быть равномерное и неравномерное;
при равномерном кодировании все символы кодируются кодами равной длины;
при неравномерном кодировании разные символы могут кодироваться кодами разной длины, это затрудняет декодирование
· закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова;
· закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова;
· условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Пример задания:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
Решение (1 способ, проверка условий Фано):
1) для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано;
2) проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»);
«прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В);
«обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит ;
«прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б);
«обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит ;
«прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит ;
Решение (2 способ, дерево):
1) построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):
2) здесь однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано);
3) теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом
4) видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т.д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано
5) хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца):
видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв
6) в заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква отказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится
Ещё пример задания:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код:
А–1, Б–000, В–001, Г–011. Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.
1) 00 2) 01 3)11 4) 010
8) заметим, что для известной части кода выполняется условие Фано – никакое кодовое слово не является началом другого кодового слова
9) если Д = 00, такая кодовая цепочка совпадает с началом Б = 000 и В = 001, невозможно однозначно раскодировать цепочку 000000: это может быть ДДД или ББ; поэтому первый вариант не подходит
10) если Д = 01, такая кодовая цепочка совпадает с началом Г = 011, невозможно однозначно раскодировать цепочку 011: это может быть ДА или Г; поэтому второй вариант тоже не подходит
11) если Д = 11, условие Фано тоже нарушено: кодовое слово А = 1 совпадает с началом кода буквы Д, невозможно однозначно раскодировать цепочку 111: это может быть ДА или ААА; третий вариант не подходит
12) для четвертого варианта, Д = 010, условие Фано не нарушено;
· условие Фано – это достаточное, но не необходимое условие однозначного декодирования, поэтому для уверенности полезно найти для всех «неправильных» вариантов контрпримеры: цепочки, для которых однозначное декодирование невозможно
Еще пример задания:
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится
14) из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный
15) последовательность БАВГ кодируется так: 01 00 10 11 = 1001011
16) разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем
1001011 = 0100 10112 = 4B 16
17) правильный ответ – 1.
· расчет на то, что при переводе тетрад в шестнадцатеричную систему можно забыть заменить большие числа (10–15) на буквы (10112 = 11, получаем неверный ответ 41116)
· может быть дан неверный ответ, в котором нужные цифры поменяли местами (расчет на невнимательность), например, B 416
· в ответах дана последовательность, напоминающая исходную (неверный ответ BACD 16), чтобы сбить случайное угадывание
Еще пример задания:
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице: