Изучение второго закона ньютона с помощью машины атвуда лабораторная работа

Изучение второго закона Ньютона с помощью машины Атвуда

Цель работы: проверить второй закон Ньютона.

Оборудование: машин Атвуда, перегрузки, электронный секундомер.

Одним из основных законов всей физики является второй закон Ньютона.

Он гласит: ускорение, которое приобретает материальная точка под действием силы, прямо пропорционально величине этой силы, обратно пропорционально

массе материальной точки и направлено в сторону действия силы:

Если на материальную точку действует несколько сил, то ускорение определяется геометрической сумой всех сил, называемой равнодействующей всех сил:

a = ∑ Fi

и направлено в сторону равнодействующей силы.

В том случае, когда силы действует не на материальную точку, а на массивное тело конечных размеров, второй закон Ньютона справедлив для центра масс этого тела. То есть ускорение центра масс тела прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе всего тела. Однако обычно тела конечных размеров имеют достаточно малые размеры по сравнению с расстоянием, которое они проходят, поэтому их вполне можно считать материальными точками.

Для проверки второго закона Ньютона нужно, прежде всего, исследовать зависимость ускорения тела от действующей на него силы. Для этого нужно

менять силу, оставляя постоянной массу тела. Для проверки зависимости ускорения от массы нужно менять массу тела при неизменной силе,

действующей на тело.

Прежде чем приступать к рассмотрению экспериментальной установки рассмотрим вспомогательную задачу: через блок перекинута нить, к концам

которой прикреплены грузы, требуется найти ускорение, с которым движутся грузы.

Для решения задач динамики следует придерживаться следующей схемы:

1. Построить схематический рисунок по задаче, на котором изобразить все силы, действующие на каждое из тел, участвующих в движении.

2. Для каждого из тел, участвующих в движении, записать второй закон

Ньютона в векторной форме (2.2). Особо нужно отметить, что в правую часть формулы (2.2) все силы входят со знаком «+» как векторы.

3. Выбрать систему координат. Система координат может быть выбрана отдельно для каждого тела, участвующего в движении. Для оптимального выбора системы координат оси координат следует направлять по тому

направлению, в котором направлено большинство сил. Это позволит уменьшить количество ненулевых проекций сил. Если все силы, действующие на данное тело, параллельны одной прямой (линейная система сил), то систему координат можно выбрать только в виде одной оси, параллельной всем силам, действующим на данное тело. Если все силы, действующие на данное тело, параллельны некоторой плоскости (плоская система сил), то достаточно выбрать только две оси, лежащие в плоскости, параллельной всем силам, действующим на данное тело. При этом опять оси координат должны быть взаимно перпендикулярны и направлены параллельно как можно большему числу сил. И, наконец, если система сил произвольная, то нужно определять все три оси координат.

4. Спроецировать каждое векторное равенство, соответствующее второму закону Ньютона, на все оси координат. Сначала спроецировать векторное равенство формально, т.е. записать это равенство заново с теми же самыми знаками у слагаемых сил, только убрать символ вектора (стрелочку над обозначением данного вектора) и указать символ проекции (т.е. индекс оси, на которую выполняется проецирование, внизу справа около обозначения вектора). После этого определить знаки проекций, т.е. выразить проекции через модули векторов с указанием конкретного знака проекции, если это возможно.

5. В результате получится несколько алгебраических уравнений, в которых некоторые параметры оказываются неизвестными. Эти уравнения и

нужно решить как систему относительно неизвестных. Однако часто бывает,

что количество неизвестных больше, чем уравнений. В этом случае система оказывается неопределённой. Для её определения нужно добавить некоторые

уравнения. Эти уравнения могут быть получены из уравнений кинематики, связывающих между собой кинематические характеристики. В качестве добавочных уравнений могут быть уравнения, полученные из некоторых

дополнительных условий. А именно, если тела связаны невесомыми связями (невесомые нити), то усилия на придание связям ускорения равны нулю. Это значит, что сила натяжения связи на её одном конце равна силе натяжения этой

связи на другом конце. Если связь нерастяжима, то перемещение одного её конца вдоль связи за некоторый промежуток времени равно перемещению её второго конца. Отсюда следует, что и скорость и ускорение концов связи вдоль

этой связи будут одинаковыми.

6. Решить систему полученных уравнений относительно требуемых неизвестных.

Применим эту схему к решению поставленной задачи.

1. Схема задачи представлена на рис. 2.1.

r r T4 T3 r r T2 T1

Рис.2.1.Силы, действующие на систему тел

На тела действует сила тяжести и сила натяжения нитей. На блок сила натяжения нитей и сила реакции со стороны оси, вокруг которой блок вращается (на рис. не показана).

2. В данном случае в движении участвуют три тела: два тела, подвешенные к нитям, и блок. Поэтому уравнений Ньютона будет три. Уравнение поступательного движения для первого тела:

и уравнение вращательного движения для блока:

где I – момент инерции блока,

εr – угловое ускорение,

– моменты сил натяжения нитей, действующих на блок.

4. Тогда проекции уравнений (2.3)-(2.5) будут иметь вид

Поскольку направление ускорения тел заранее неизвестно (оно зависит от соотношения масс тел), то конкретизировать их знаки не будем. Ускорение

значит, проекция его положительна. Силы r r

направлены вверх, значит, их

проекции отрицательны. Момент силы

T4 относительно оси вращения

проекции отрицательна. Так что уравнения (2.6)-(2.7) перепишутся по-другому:

В данных уравнениях мы выразили проекции векторов через их модули, о чём говорит тот факт, что обозначения величин не имеют ни символа вектора, ни символа проекции.

Моменты сил по модулю равны произведению модуля сил на плечо:

где R есть радиус блока.

Так что вместо третьего уравнения можно использовать уравнение:

5. Неизвестными в этой системе уравнений являются следующие: ускорения трёх тел, участвующих в движении; величины сил натяжения нити в начале и в конце прямолинейного участка, таких неизвестных четыре. Всего получается 7 неизвестных, а уравнений только три. Так что требуется ещё 4 уравнения. Для отыскания этих уравнений воспользуемся прежде всего тем фактом, что нить невесома. Тогда силы натяжения на разных концах нитей будут равны:

Это и есть недостающее уравнение системы. Выпишем теперь все уравнения:

Источник

Краткая теория эксперимента

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

на заседании кафедры физики

Методические указания

к лабораторной работе № 4

ИЗУЧЕНИЕ ВТОРОГО ЗАКОНА НЬЮТОНА

С ПОМОЩЬЮ МАШИНЫ АТВУДА»

Методические указания к лабораторной работе № 4 «Изучение второго закона Ньютона с помощью машины Атвуда». – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 8 с.

Методические указания содержат краткую теорию метода, порядок выполнения лабораторной работы, требования техники безопасности, требования к оформлению результатов, а также перечень контрольных вопросов и тестов.

Предназначены для выполнения лабораторной работы по программе курса общей физики для студентов всех специальностей РГСУ.

Составители: проф. Н.Н. Харабаев,

Рецензент доц. Ю.И. Гольцов

Редактор Н.Е. Гладких

Темплан 2011 г., поз. ___

Подписано в печать ____). Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л 0,5. Тираж 100 экз. Заказ

Ростовского государственного строительного университета.

334022, Ростов-на-Дону, ул. Социалистическая, 162

строительный университет, 2011

Лабораторная работа №4

ИЗУЧЕНИЕ ВТОРОГО ЗАКОНА НЬЮТОНА

С ПОМОЩЬЮ МАШИНЫ АТВУДА

Цель работы: на опыте изучить действие основного закона динамики поступательного движения.

Приборы и принадлежности: установка «машина Атвуда», набор грузов, секундомер, линейка.

Краткая теория эксперимента

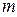
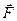
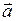
Основной закон динамики поступательного движения (второй закон Ньютона): если на тело массой действует сила , то это тело приобретает ускорение , величина которого прямо пропорциональна величине действующей силы и обратно пропорциональна массе данного тела.

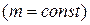
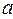
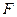
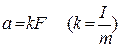
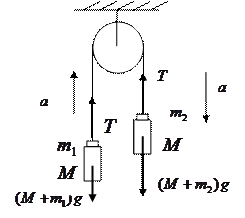Согласно этому закону для какого-либо тела с неизменной массой величина ускорения линейно зависит от величины действующей силы , то есть . Линейная зависимость величины ускорения от величины действующей силы может быть проверена экспериментально с помощью «машины Атвуда» (рис.1).

Рис.1. Принципиальная схема «машины Атвуда»

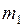
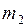
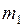
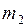
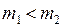
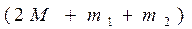
Через легкий блок перекинута тонкая нить, на концах которой подвешены грузы массой M каждый. На левый и правый грузы помещают перегрузки массами и , причем ¹ (например, ). В этом случае система грузов массой придет в движение.

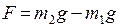
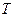
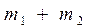
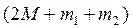
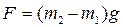
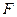
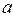
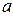
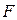
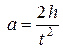
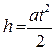
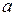
Результирующая сила, вызывающая ускорение движения этой системы грузов, равна разности сил тяжести перегрузков m₁ и m₂, лежащих на правом и левом грузах M : . Это выражение справедливо, если пренебречь массой блока и трением в оси блока (в этом случае силы натяжения для нитей слева и справа одинаковы по величине). Изменяя массы перегрузков m₁ и m₂ так, чтобы их сумма сохранялась и соответственно сохранялась масса всей системы грузов , получим несколько значений силы , вызывающей ускорение системы. Для каждого значения силы определим ускорение движения и найдем зависимость величины от величины . Величину ускорения грузов можно определить опытным путем с помощью формулы , полученной из , где h – путь, пройденный телом за время t после начала равноускоренного движения с ускорением .

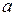
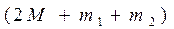
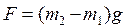
По зависимости величины ускорения для системы грузов массой от величины результирующей силы проверим справедливость 2-го закона Ньютона.

Порядок выполнения работы

1. Подготовим таблицы для результатов измерений (таблицы 1, 2).

3. С помощью линейки измерим h – расстояние, которое проходят грузы. Время движения грузов t измерим с помощью секундомера, причем для уменьшения погрешности измерения времени t повторим эксперимент пять раз и вычислим среднее значение времени движения грузов под действием данной силы F, как среднее арифметическое значение пяти последовательных измерений: .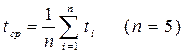

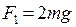
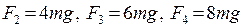
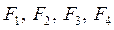
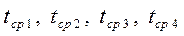
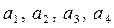
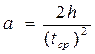
4. Перекладывая по одному перегрузку с правого груза на левый, получаем результирующую силу последовательно равной после силам . Измерим по пять раз время движения грузов под действием каждой силы , найдем средние значения и вычислим соответствующие значения ускорения , используя формулу .

5. Оценим погрешности определения ускорений .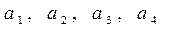

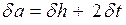
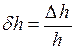
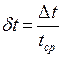
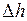
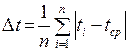
Поскольку определение величины ускорения следует из косвенных измерений, то используем зависимость относительной погрешности da от относительных погрешностей d h и d t, где

— относительная погрешность измерения расстояния;

— относительная погрешность измерения времени;

— абсолютная погрешность измерения расстояния h (за абсолютную погрешность принимаем половину цены наименьшего деления линейки); — абсолютная погрешность измерения времени.

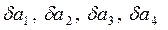
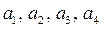
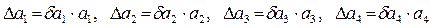
Вычислив относительные погрешности , находим для каждого значения ускорения абсолютные погрешности .

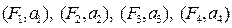
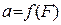
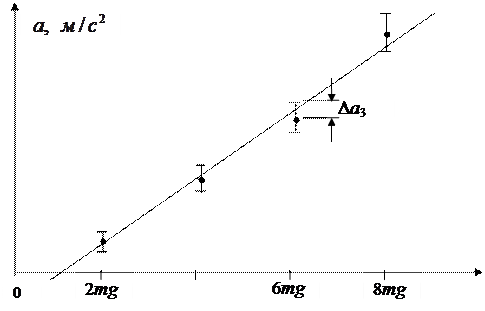6. По точкам с учетом погрешностей экспериментального определения ускорения построим график (рис. 2).

Рис. 2. График экспериментальной зависимости

Контрольные вопросы

1. Дать определения пути, перемещения, скорости и ускорения.

2. Дать определения силы и массы.

3. Инерциальные и неинерциальные системы отсчета.

4. Первый, второй и третий законы Ньютона.

5. Основной закон динамики поступательного движения в дифференциальной форме.

6. Как с помощью построенного графика 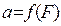определить общую массу системы?

7. График зависимости 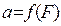в данной работе не проходит через начало координат! Почему?

8. Прямые и косвенные измерения.

9. Абсолютная и относительная погрешности прямых измерений.

Источник

Проверка второго закона Ньютона на машине Атвуда

ЦЕЛЬ: установить зависимость ускорения системы от действующей силы; определить из полученной зависимости массу системы.

ОБОРУДОВАНИЕ: экспериментальная установка FRM ; электронный секундомер с фотоэлектрическими датчиками, линейка.

ОСНОВЫ ТЕОРИИ

где р = m v  импульс тела,

Для малых скоростей массу можно считать постоянной и вынести из-под знака дифференциала:

Масса. Опыт показывает, что одинаковые воздействия вызывают у разных тел различные изменения скорости. Одному и тому же телу различные силы сообщают различные ускорения. Однако отношение силы к ускорению для каждого тела всегда равно одной и той же величине:

Следовательно, масса является количественной мерой инертности тел. Под инертностью понимается свойство тел противиться изменению скорости. Отношение F/a = const справедливо только при достаточно малых скоростях.

где m 0 – константа, называемая массой покоя (масса тела при при v = 0),

с  скорость света в вакууме.

Определенная в формуле (5) масса тела m является функцией его скорости:

При v « c масса тела мало отличается от m 0 и соотношение (4) можно считать справедливым. Уравнения (1) и (3) формально эквивалентны. Однако это имеет место только при малых скоростях движения. Оказалось, что в релятивисткой динамике уравнения (1) и (2) остаются справедливыми, если массу определять в соответствии с выражением (6). Соотношение (3) при больших скоростях перестает быть справедливым.

МЕТОДИКА ЭКСПЕРИМЕНТА

Рис. 1. Машина Атвуда.

Запишем второй закон Ньютона для груза m 1 :

Спроецируем его на ось x 1 :

Аналогично для груза m 2 :

В проекциях на ось x 2 : :

В силу принятых выше допущений

Складывая уравнения (7) и (8), получим:

Введем обозначения для суммарной массы системы:

и эффективной силы, численно равной разности сил тяжести грузов:

Тогда формула (9) примет вид:

с коэффициентом пропорциональности, обратным полной массе системы:

Тогда выражение (10) примет вид:

Логическая схема эксперимента

Для проверки пропорциональности между a и F каждая из этих величин должна быть определена независимым способом.

ВЫПОЛНЕНИЕ РАБОТЫ

1. Определите взвешиванием массы грузов и перегрузков.

2. Установите левый груз в крайнее нижнее положение.

3. Поместите на правый груз большой перегрузок, на левый груз  все маленькие перегрузки.

4. Отпустите левый груз и измерьте время движения грузов, а также путь, пройденный одним из них.

5. Перенося по одному перегрузку с левого груза на правый, повторяйте опыт до тех пор, пока на левом грузе не останется ни одного перегрузка. Результаты измерений занесите в таблицу.

Источник

Проверка второго закона Ньютона с помощью машины Атвуда. (Лабораторная работа 4)

Приборы и принадлежности: машина Атвуда с платформой и электромагнитом, секундомер, набор грузов и перегрузков.

Теория метода и описание прибора

Машина Атвуда представляет собой вертикальную рейку со шкалой А, прикрепленную к стене или укрепленную на массивном чугунном треножнике (рис. 2.3).

Рис.2.3

Рис.2.4

На верхнем конце рейки имеется легкий алюминиевый блок В, вращающийся с малым трением. Через блок перекинута нить, на концах которой подвешиваются грузы С и С’ разных масс М₁ и М₂.

Масса грузов слагается из массы основного (большого) груза с подвеской и добавочных грузиков (перегрузков) m:

Вдоль рейки может перемещаться платформа Д. Левый груз С’ в нижнем (начальном) положении удерживается электромагнитом Э. Тумблер К, укрепленный сбоку на рейке, находится при этом в положении «вниз».

При переключении тумблера в положение «вверх» электромагнит отключается, вся система грузов приходит в движение.

При этом одновременно включается секундомер. В момент удара груза С о платформу Д секундомер выключается.

Рассмотрим движение грузов массой М₁ и М₂ на машине Атвуда (рис.2.4). Каждый из рассматриваемых грузов находится под действием двух сил: силы тяжести P = mg и силы натяжения Т (силами трения пренебречь). Применяя II закон Ньютона для каждого груза, получим

(2.16)

Если считать, что нить и блок невесомы, то сила натяжения нити по всей длине одинакова:

Вследствие нерастяжимости нити, ускорения обоих грузов равны по величине и противоположны по направлению: .

Тогда уравнение (2.16) можно переписать в виде

(2.17)

Проецируя эти уравнения на вертикальное направление, получим систему

Решая систему уравнений относительно а, находим

(2.18)

Из формулы (2.18) видно, что сила F, которая сообщает ускорение системе грузов на нити общей массой М_с = М₁+ М₂, равна разности сил тяжести грузов P₂ – P₁, находящихся на концах нити, то есть

Ускорение системы а всегда меньше ускорения свободного падения g и может быть определено экспериментально.

Если F=(М₂ – М₁)g во время движения не изменяется, то движение системы будет равноускоренно, и для него справедливо уравнение:

где S – расстояние, проходимое грузом Р за время t.

Измеряя S и t, можно определить ускорение:

.

Из-за весомости блока и наличия сил трения в оси блока, ускорение, наблюдаемое на опыте, будет меньше, чем определяемое формулой (2.18).

Перекладывая перегрузки с одного конца нити на другой (но не снимая с нити), можно менять величину движущей силы F, не меняя общей массы системы М_с.

Меняя же массу основных грузов m₀ при неизменном положении перегрузков, можно менять общую массу системы М_с при постоянной движущей силы F.

Порядок выполнения работы и обработка результатов

Измерений

Задание 1. Проверка закона пути _.

1. Включить секундомер и электромагнит в сеть. На концы нити подвесить основные грузы одинаковой массы m₀. На правый конец нити добавить перегрузок m =5… 10 г.

2. Левый груз С’ опустить до соприкосновения с электромагнитом. Тумблер К установить в положение «вниз». На расстоянии S (не менее 60 см) от конца нижнего края правого груза Р закрепить платформу Д.

3. Переводом тумблера К в положение «вверх» выключить ток в обмотке электромагнита. Одновременно включится секундомер и грузы придут в движение. После остановки секундомера снять его показания.

4. Измерения времени t для высоты S провести 3 – 5 раз.

5. Повторить измерения согласно пунктам 2–4 для двух других высот S, изменяя высоту передвижением платформы Д.

6. Все данные измерений занести в табл. 2.2.

7. Оценить погрешность измерения ускорения.

Задание 2. Проверка следствий II закона Ньютона

а) Проверка соотношения: при m = const. (2.19)

1. На концы нити подвесить по основному грузу одинаковой массы (30–50 г) и 2 – 3 перегрузка так, чтобы разность сил тяжести грузов на концах нити была не более 20 г. Установить платформу Д в определенном положении.

3. Провести измерения согласно пунктам 2–4 задания 1.

5. Повторить опыт (3–5 раз) для нового положения грузов. Данные измерений занести в табл. 2.3.

б) Проверка соотношения: при F = const. (2.20)

2. Провести измерения времени движения (3–5 раз) для выбранной высоты S.

4. Повторить опыт (3–5 раз) для новой системы грузов. Все данные измерений занести в табл. 2.3.

Источник